Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Investigación & Desarrollo
versión impresa ISSN 1814-6333versión On-line ISSN 2518-4431
Inv. y Des. vol.1 no.15 Cochabamba 2015
ARTÍCULOS - INGENIERÍAS
MODELOS REALISTAS EN LA VERIFICACIÓN DEL ESFUERZO CORTANTE EN ELEMENTOS DE HORMIGÓN ARMADO
REALISTIC MODELS FOR VERIFYING SHEAR IN REINFORCED CONCRETE MEMBERS
Francisco Aguirre, Sebastián Ontiveros y Alejandra Orellana
Centro de Investigaciones en Materiales y Obras Civiles (CIMOC)
Universidad Privada Boliviana
faguirre@upb.edu
(Recibido el 15 de junio de 2015, aceptado para publicación el 30 de junio 2015)
RESUMEN
Con el crecimiento acelerado de las resistencias del hormigón a compresión, es necesario considerar modelos de cálculo de las estructuras rigurosos. Las normas de cálculo de estructuras de hormigón armado tienen sus modelos matemáticos basados principalmente en ensayos de laboratorio y usualmente son empíricos. Muchos códigos tienen modelos de cálculo de estructuras bastante conservadores y desactualizados, porque resulta complejo estudiar todas las variables que influyen en el comportamiento de un elemento sometido a esfuerzos cortantes combinados con otros tipos de esfuerzos.
Este trabajo está basado en investigaciones de Collins donde propuso la Teoría del Campo de Compresión (TCC), más adelante Vecchio y Collins desarrollaron la Teoría del Campo de Compresión Modificada (TCCM) y años más tarde Bentz, Vecchio y Collins presentaron la Teoría del Campo de Compresión Modificada Simplificada (TCCMS), siendo este último un poco menos riguroso pero más simple de ser aplicado.
En este artículo se proponen modelos basados en la TCCM y TCCMS y se muestra resultados de ejemplos aplicando estos modelos comparándolos con las normas ACI 318-11 y CAN23.3-04. En el cálculo de la armadura transversal, la variación entre la TCCM y las normas ACI 318-11 y CAN23.3-04 fue de 33% y 64% respectivamente y la variación entre la TCCMS y las normas ACI 318-11 y CAN23.3-04 fue de 2% y 25% respectivamente.
Palabras Clave: Resistencia, Cortante, Hormigón Armado.
ABSTRACT
As strength in concrete in stress grows fast, it is necessary to consider more accurate structural method. Most of the modern codes are based on the analysis of laboratory tests and they use very empirical expressions. The different methods used on these codes remain conservative and have been left outdated because analyzing each and every variable that influences shear strength is a complex matter.
This article is based on the research made by Collins with their Compression Field Theory (CFT), later Vecchio and Collins presented the Modified Compression Field Theory (MCFT). Years later Bentz, Vecchio and Collins developed the Simplified Modified Compression Field Theory (SMCFT), being this one less accurate but easier to apply.
This article presents models based on MCFT and SMCFT and shows examples using MCFT and SMCFT compared to the results in the same example using ACI 318-11 and CAN23.3-04. These results show that stirrups variation between MCFT and ACI 318-11and CAN23.3-04 gave 33% and 64% respectively, and the variation between SMCFT and ACI 318-11 and CAN23.3-04 gave 2% and 25% respectively.
Keywords: Strength, Shear, Reinforced Concrete.
1. INTRODUCCIÓN
El diseño a esfuerzos cortantes de elementos de hormigón armado viene determinado por un gran número de variables, entre las cuales se encuentra: su geometría, la resistencia de sus materiales, sus dimensiones, dimensiones de los agregados, las cargas aplicadas, la flexión, el esfuerzo axial y la torsión actuantes combinadas con el cortante, etc. En el congreso de 1970 de la Fédération Internationale de la Précontrainte (FIP), Fritz Leonhardt dijo que la principal razón por la cual se tienen teorías deficientes para torsión y cortante es justamente porque estos esfuerzos se ven influenciados por más de 20 variables y que la mayoría de los resultados de laboratorio son imparciales o de baja calidad [4].
Muchos de los experimentos de laboratorio que se realizan para analizar los esfuerzos cortantes son aquellos que se aplica una o dos cargas puntuales en una viga de hormigón armado o sin armadura transversal. Sin embargo, lo más importante para el diseño a cortante es adoptar un modelo que se aproxime suficientemente a la realidad. El modelo más conocido y que fue el más aplicado es el modelo de la cercha con ![]() (Figura 1).
(Figura 1).
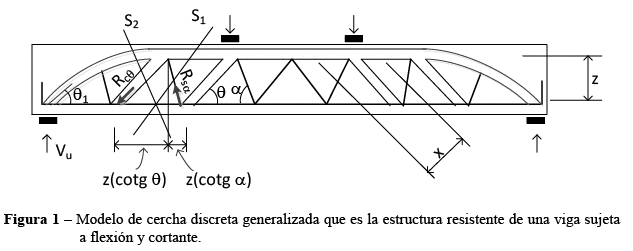
2. EVOLUCIÓN DEL DISEÑO A CORTANTE
La idea de utilizar modelos de cercha para el análisis de cortante comenzó a ser desarrollado hace más de 100 años. Se asume que el hormigón entre fisuras diagonales en el alma de una viga en combinación con la armadura transversal resiste el esfuerzo cortante. Este modelo aún sigue siendo muy aceptado y utilizado hoy en día por la simplicidad de sus cálculos.
En 1950, el Instituto de Concreto Americano (ACI por sus siglas en inglés) se dedicó a desarrollar nuevos modelos mejorados especialmente porque varias vigas de dos oficinas de la Fuerza Aérea de los Estados Unidos se desplomaron. En 1962, se propusieron nuevos métodos de cálculos, los cuales son aún la base de la ACI [5].
Según Kaufmann[6], por los años 50 fue aplicada la teoría de la plasticidad a estructuras de hormigón. Con este modelo, el principio de cerchas discretas se puede implementar a campos de compresión discontinuos o regiones D y se puede aplicar los estados límites a regiones con interrupciones de continuidad como quiebres, huecos, muros, vigas peraltadas, etc.
La Teoría del Campo a Compresión (TCC) desarrollada por Collins [1], fue un gran avance hacia el desarrollo de una teoría racional para cortante. Esta teoría considera condiciones de deformación en el alma de la viga para determinar el ángulo de inclinación θ de la biela comprimida mediante la relación ![]() , donde estas variables se muestran en la Figura 2. En este método no se considera la tracción existente entre las fisuras diagonales, pero ya presentaba buena precisión en la determinación de la resistencia a cortante de elementos de hormigón.
, donde estas variables se muestran en la Figura 2. En este método no se considera la tracción existente entre las fisuras diagonales, pero ya presentaba buena precisión en la determinación de la resistencia a cortante de elementos de hormigón.
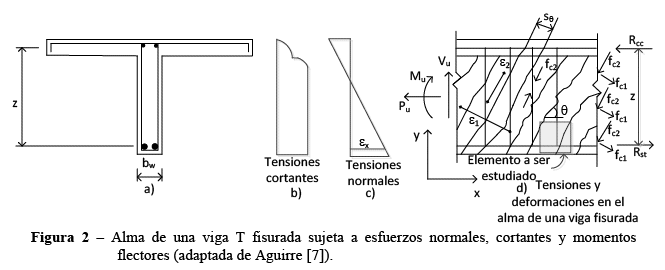
Más adelante, Vecchio y Collins [2], desarrollaron la Teoría del Campo de Compresión Diagonal Modificado (TCCM) a partir de ensayos en paneles de 89 cm x 89 cm por 7 cm de espesor cargados en su propio plano a cortante puro y cortante con esfuerzos axiales. Entre los resultados de estos ensayos, se ha considerado al hormigón fisurado como un nuevo material. Se desarrolla en base a las ecuaciones de equilibrio con tensiones normales y cortantes promedios, ecuaciones de compatibilidad de deformaciones y las relaciones constitutivas de los materiales, todas éstas aplicadas en un elemento del alma de la viga (Figura 2). También analiza el equilibrio en una fisura diagonal (Figura 8). De manera interactiva, se obtiene la inclinación ![]() de la biela comprimida y el factor de debilitamiento de las tensiones de tracción entre las fisuras
de la biela comprimida y el factor de debilitamiento de las tensiones de tracción entre las fisuras ![]() , entre otros parámetros de diseño. Mediante la TCCM se lograron hallar resultados muy precisos de la resistencia a cortante en paneles de hormigón armado que en algunos casos alcanzaban una relación experimental-calculado de 1,01.
, entre otros parámetros de diseño. Mediante la TCCM se lograron hallar resultados muy precisos de la resistencia a cortante en paneles de hormigón armado que en algunos casos alcanzaban una relación experimental-calculado de 1,01.
Finalmente, Bentz, Vecchio y Collins [3], presentaron la TCCMS que es una simplificación del TCCM partiendo de las mismas hipótesis y ecuaciones para hallar ![]() y
y ![]() , este modelo presenta menos interacciones. La norma AASHTO LRFD [8] adopta este modelo y en lugar de interacciones presenta tablas para las diversas situaciones. Con este método, a pesar de tener un procedimiento más práctico, los resultados hallados por Bentz, Vecchio y Collins [3] en paneles de hormigón armado seguían siendo considerablemente precisos alcanzando en algunos casos una relación de la resistencia a cortante de 1,11.
, este modelo presenta menos interacciones. La norma AASHTO LRFD [8] adopta este modelo y en lugar de interacciones presenta tablas para las diversas situaciones. Con este método, a pesar de tener un procedimiento más práctico, los resultados hallados por Bentz, Vecchio y Collins [3] en paneles de hormigón armado seguían siendo considerablemente precisos alcanzando en algunos casos una relación de la resistencia a cortante de 1,11.
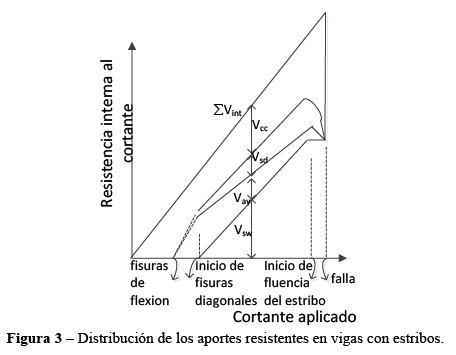
En todos los estudios de la resistencia al cortante de elementos a flexión con armadura transversal, se considera que una parte del cortante es absorbido por lo que comúnmente se denomina aporte del hormigón en la resistencia al cortante y todo el esfuerzo cortante en el caso de elementos sin armadura transversal. El presente estudio es justamente para determinar, entre otros resultados, el valor de este aporte. Tradicionalmente, el aporte proviene de tres efectos, que en orden de importancia son: el aporte del hormigón comprimido no fisurado, la fricción entre los agregados y la armadura longitudinal trabajando como perno a corte con su efecto de dovela.
3. APORTE DEL HORMIGÓN EN LA RESISTENCIA A CORTANTE
En los primeros modelos de cercha para el cálculo de la resistencia a esfuerzos cortantes, sólo se consideraba el aporte de la armadura transversal ![]() en la resistencia al esfuerzo cortante. Actualmente, se sabe que el hormigón aporta en la resistencia al cortante a través de la armadura longitudinal trabajando con su efecto de dovela
en la resistencia al esfuerzo cortante. Actualmente, se sabe que el hormigón aporta en la resistencia al cortante a través de la armadura longitudinal trabajando con su efecto de dovela ![]() , esta acción aparece cuando ya se tienen aberturas en las fisuras diagonales razonables. Para aberturas moderadas de las fisuras diagonales, el efecto de dovela es pequeño frente al efecto de la componente vertical de la trabazón de los agregados
, esta acción aparece cuando ya se tienen aberturas en las fisuras diagonales razonables. Para aberturas moderadas de las fisuras diagonales, el efecto de dovela es pequeño frente al efecto de la componente vertical de la trabazón de los agregados ![]() para la misma abertura, Figura 3. En el hormigón comprimido no fisurado, se ha verificado que su aporte en la resistencia al cortante
para la misma abertura, Figura 3. En el hormigón comprimido no fisurado, se ha verificado que su aporte en la resistencia al cortante![]() es porque se generan esfuerzos principales diagonales que forman fisuras cortas y en presencia de la armadura transversal componen su resistencia al cortante, normalmente la falla ocurre cuando la armadura transversal alcanza la fluencia, Figura 3.
es porque se generan esfuerzos principales diagonales que forman fisuras cortas y en presencia de la armadura transversal componen su resistencia al cortante, normalmente la falla ocurre cuando la armadura transversal alcanza la fluencia, Figura 3.
El hormigón no fisurado actúa como un anclaje de los refuerzos transversales y de las diagonales comprimidas. Estas diagonales son comprimidas con una tensión ![]() (Figura 2) y también aportan a la resistencia transmitiendo las fuerzas de la cara superior del elemento hacia el cordón inferior y los apoyos. Estas bielas al encontrarse en compresión axial, tienden a expandirse lateralmente, lo cual genera presiones laterales y, de esta manera, se transmiten tensiones de tracción
(Figura 2) y también aportan a la resistencia transmitiendo las fuerzas de la cara superior del elemento hacia el cordón inferior y los apoyos. Estas bielas al encontrarse en compresión axial, tienden a expandirse lateralmente, lo cual genera presiones laterales y, de esta manera, se transmiten tensiones de tracción ![]() a través de las fisuras (son tensiones principales entre fisuras). Estas tensiones permiten que las dos caras de la fisura se sujeten entre si y aporten con su fricción para resistir el esfuerzo cortante.
a través de las fisuras (son tensiones principales entre fisuras). Estas tensiones permiten que las dos caras de la fisura se sujeten entre si y aporten con su fricción para resistir el esfuerzo cortante.
Simplificadamente, se puede asumir que los elementos del alma de los paneles ensayados por Vecchio y Collins[2] y elementos del alma de vigas se comportan como un problema bidimensional, podrían ser considerados como elementos de membrana y que su campo de tensiones se corresponda con su campo de deformaciones suponiendo un estado plano de tensiones (EPT). En este trabajono se limitará a obtener las relaciones constitutivas para el hormigón fisurado y para la armadura de refuerzo, será analizado un modelo físico del aporte del hormigón en la resistencia al cortante.
4. MODELO QUE CORRESPONDE A UN ELEMENTO MEMBRANAL
Considerando que los elementos estructurales están sujetos a fuerzas externas y gravitacionales, surgen esfuerzos distintos en el interior de los diferentes puntos del cuerpo. La ecuación (1), escrita en forma tensorial, muestra la relación entre estos esfuerzos y su campo correspondiente de deformaciones para un punto del interior de un elemento tridimensional. La expresión entre las tensiones y deformaciones se encuentra en su forma más general y vale inclusive para materiales dependientes del tiempo.
![]()
donde ![]() es el tensor de tensiones,
es el tensor de tensiones, ![]() es el tensor de deformaciones(estos tensores son simétricos y de 3 x 3 términos) y
es el tensor de deformaciones(estos tensores son simétricos y de 3 x 3 términos) y ![]() la matriz de elasticidad que es un tensor de cuarta orden de 81 constantes elásticas.
la matriz de elasticidad que es un tensor de cuarta orden de 81 constantes elásticas.
Con la relación constitutiva de la ecuación (1) se consigue obtener el número suficiente de ecuaciones para resolver el problema. El problema en el caso más general, consiste en resolver 15 ecuaciones (3 ecuaciones diferenciales del equilibrio interno, 6 ecuaciones diferenciales de compatibilidad de deformaciones y 6 ecuaciones constitutivas) para obtener las 15 incógnitas para cada punto del interior del cuerpo (3 desplazamientos, 6 tensiones y 6 deformaciones específicas).
En el caso de un elemento del alma, Figura 2 y Figura 4, se puede asumir que se tiene sólo desplazamientos en un plano (no existen tensiones ni deformaciones en la dirección z), son estados bidimensionales que representan una aproximación de un estado tridimensional.
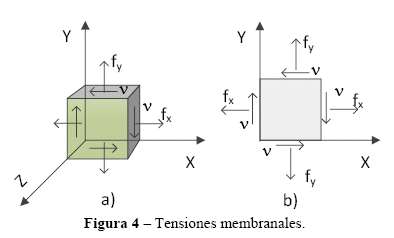
Para determinar el estado de tensiones alrededor de un punto es necesario conocer los términos de la matriz simétrica del estado de tensiones o el llamado tensor de tensiones. La matriz del estado de tensiones debe satisfacer las ecuaciones de equilibrio que gobiernan la distribución de tensiones en el interior del cuerpo deformable, las ecuaciones de equilibrio de este elemento diferencial se pueden encontrar en Timoshenko y Goodier[9]. La ecuación (2) muestra el tensor de tensiones de un elemento del alma de la viga.
![]()
De la misma manera que surgen esfuerzos solicitantes en el interior de un cuerpo, se tienen variaciones entre las distancias entre los diferentes puntos. La Figura 5 muestra las deformaciones de un elemento del alma donde se asume que sus lados permanecen rectos y paralelos después de la deformación.
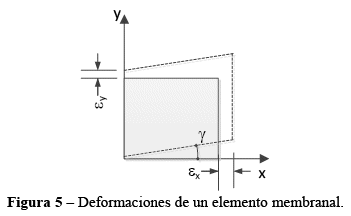
En un EPT, es necesario considerar las deformaciones específicas lineares ![]() y la distorsión
y la distorsión ![]() referente a las direcciones x yy. El estado plano de tensiones deberá satisfacer las ecuaciones de compatibilidad (Timoshenko and Goodier[9]).
referente a las direcciones x yy. El estado plano de tensiones deberá satisfacer las ecuaciones de compatibilidad (Timoshenko and Goodier[9]).
La ecuación (3) presenta la matriz del estado de deformaciones o también llamado de tensor de deformaciones.
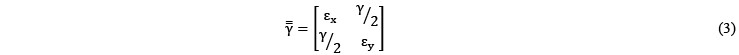
Para el hormigón no fisurado e isotrópico, la ecuación (4) presenta matricialmente la relación entre las tensiones y deformaciones para un EPT.
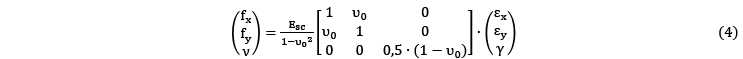
donde, ![]() es el módulo de deformación secante y
es el módulo de deformación secante y ![]() es el coeficiente de Poisson del hormigón.
es el coeficiente de Poisson del hormigón.
Cuando el hormigón se fisura, la matriz de elasticidad se vuelve anisotrópica, con ![]() . En esta situación,
. En esta situación, ![]() en dirección perpendicular a la fisura es nulo en la fisura y entre fisuras su valor es proporcional al módulo de deformación secante pero en la dirección perpendicular a las fisuras (dirección traccionada del sistema de coordenadas de las fisuras diagonales).
en dirección perpendicular a la fisura es nulo en la fisura y entre fisuras su valor es proporcional al módulo de deformación secante pero en la dirección perpendicular a las fisuras (dirección traccionada del sistema de coordenadas de las fisuras diagonales).
Para el caso de los paneles de hormigón fisurado y atravesado por armaduras transversales y longitudinales, la matriz de elasticidad tendría una forma muy diferente. En el siguiente parágrafo, se presentan las relaciones constitutivas de forma experimental para un elemento del alma de la viga.
5. TEORÍA DEL CAMPO DE COMPRESIÓN MODIFICADO
Esta teoría muestra un modelo analítico que representa el comportamiento del hormigón, armado en direcciones perpendiculares y discretizado como un elemento de membrana sujeto a tensiones normales y cortantes (Figura 6). En esta teoría se representa el alma de la viga como un conjunto de diagonales comprimidas entre fisuras diagonales, atravesada por estribos y armadura de piel. Es posible incluir las tensiones de tracción existente entre fisuras diagonales como una manera de introducir el aporte del hormigón en la resistencia al cortante a través de las fisuras diagonales. Esta teoría explica físicamente el aporte del hormigón en la resistencia al cortante sin mayores consideraciones sobre los porcentajes de cada tipo de aporte. Esta teoría se aplica para regiones con continuidad o regiones B.
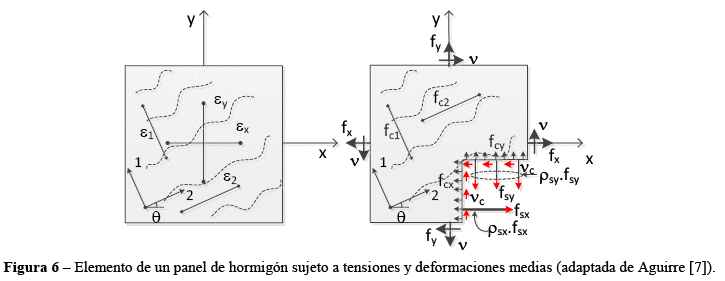
El modelo, para la simplicidad de sus cálculos, considera el promedio de tensiones y deformaciones en un panel con varias fisuras, las fisuras diagonales pueden transmitir esfuerzos cortantes y normales de compresión, Figura 7, para cada estado de deformación sólo existe un estado de tensión.
La TCCM está fundamentada en las relaciones de compatibilidad de las deformaciones medias en el hormigón y en las armaduras, relaciones de equilibrio entre las tensiones medias en el hormigón y en las armaduras y relaciones constitutivas del hormigón fisurado y de las armaduras [7].
De las relaciones de compatibilidad de deformaciones analizadas por Aguirre [7], la ecuación (5) muestra la relación entre las deformaciones específicas principales ![]() con las deformaciones específicas verticales
con las deformaciones específicas verticales ![]() (considerada igual a la de los estribos) y horizontales
(considerada igual a la de los estribos) y horizontales ![]() (considerada igual a la de la armadura longitudinal traccionada). Estas relaciones fueron obtenidas utilizando el círculo de Mohr de deformaciones. Ambas expresiones son función del ángulo de inclinación
(considerada igual a la de la armadura longitudinal traccionada). Estas relaciones fueron obtenidas utilizando el círculo de Mohr de deformaciones. Ambas expresiones son función del ángulo de inclinación ![]() de la tensión principal de compresión
de la tensión principal de compresión ![]() (considerada con igual inclinación a la deformación específica principal de compresión
(considerada con igual inclinación a la deformación específica principal de compresión ![]() , Figura 2).
, Figura 2).
![]()
De las ecuaciones de equilibrio en la TCCM analizadas por Aguirre[7], equilibrando las tensiones en las direcciones x y y, considerando el diagrama de cuerpo libre de la Figura 6 y utilizando el círculo de Morh se obtiene las relaciones de las tensiones normales y cortantes con la tensión principal de tracción ![]() (particularmente, todos los materiales contribuyen con su resistencia, Figura 6). Las ecuaciones (6) y (7) muestran estas igualdades,
(particularmente, todos los materiales contribuyen con su resistencia, Figura 6). Las ecuaciones (6) y (7) muestran estas igualdades,
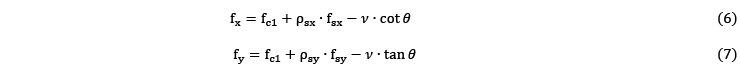
donde ![]() son las tensiones en el hormigón,
son las tensiones en el hormigón, ![]() son las cuantías geometrías de las armaduras y
son las cuantías geometrías de las armaduras y ![]() son las tensiones de trabajo de las armaduras. Como se mostrará posteriormente, los valores de las tensiones y deformaciones principales pueden ser obtenidos mediante ensayos de laboratorio.
son las tensiones de trabajo de las armaduras. Como se mostrará posteriormente, los valores de las tensiones y deformaciones principales pueden ser obtenidos mediante ensayos de laboratorio.
De la ecuación (7) es posible retirar el término de la tensión normal vertical ![]() , porque el presente estudio corresponde a una región de una viga a flexión y
, porque el presente estudio corresponde a una región de una viga a flexión y![]() influye muy poco. La ecuación(8)presenta la resistencia al esfuerzo cortante que viene de resolver la ecuación(7) para la tensión tangencial
influye muy poco. La ecuación(8)presenta la resistencia al esfuerzo cortante que viene de resolver la ecuación(7) para la tensión tangencial ![]() , ya sin el término
, ya sin el término ![]() ,
,
![]()
En la ecuación 8 se destaca tanto el aporte del hormigón en la resistencia al cortante![]() como de la armadura transversal
como de la armadura transversal ![]() .
.
Con las relaciones constitutivas estudiadas por Aguirre [7], se completa el número de ecuaciones para obtener las respuestas necesarias. Estas relaciones son entre las tensiones medias y las deformaciones específicas medias para el hormigón fisurado y la armadura. Para la armadura se admite un estado de tensión axial, o sea, un comportamiento elasto-plástico perfecto ![]() , donde
, donde ![]() son: la tensión de trabajo, la deformación específica, el módulo de elasticidad y la tensión de fluencia de la armadura respectivamente.
son: la tensión de trabajo, la deformación específica, el módulo de elasticidad y la tensión de fluencia de la armadura respectivamente.
Para el hormigón, en Vecchio y Collins[2], Bentz, Vecchio y Collins [3], Collins, et al.[10] y Vecchio[11], fueron realizados ensayos en paneles de hormigón con armaduras perpendiculares entre si y distribuida uniformemente en ambas direcciones para diversas situaciones de carga. Durante los ensayos, las tensiones ![]() eran conocidas y sus correspondientes deformaciones
eran conocidas y sus correspondientes deformaciones ![]() fueron medidas para cada etapa de carga. Fue posible construir un círculo de Morh en cada etapa de carga, obteniéndose las tensiones y deformaciones principales para cada etapa. De esa manera, se logró las relaciones constitutivas durante los ensayos para la tracción y compresión. Durante los ensayos, las tensiones en las armaduras fueron obtenidas por medición directa.
fueron medidas para cada etapa de carga. Fue posible construir un círculo de Morh en cada etapa de carga, obteniéndose las tensiones y deformaciones principales para cada etapa. De esa manera, se logró las relaciones constitutivas durante los ensayos para la tracción y compresión. Durante los ensayos, las tensiones en las armaduras fueron obtenidas por medición directa.
Con los resultados de estos ensayos, se estableció que la tensión principal de compresión de la biela del hormigón ![]() , está en función de la deformación principal promedio a compresión
, está en función de la deformación principal promedio a compresión ![]() y de la deformación promedio a tracción
y de la deformación promedio a tracción ![]() . Fue verificado que luego de que se produjeron las fisuras diagonales, el hormigón trasmite esfuerzos de tracción entre las fisuras.
. Fue verificado que luego de que se produjeron las fisuras diagonales, el hormigón trasmite esfuerzos de tracción entre las fisuras.
La ecuación (9) muestra la expresión de ![]() en función a la deformación principal
en función a la deformación principal ![]() , donde aparece el factor
, donde aparece el factor ![]() (factor de debilitamiento) que provoca un abatimiento de la curva de un ensayo a compresión de una probeta cilíndrica, de esta manera se considera que el hormigón entre fisuras y atravesado por armaduras como un hormigón debilitado,
(factor de debilitamiento) que provoca un abatimiento de la curva de un ensayo a compresión de una probeta cilíndrica, de esta manera se considera que el hormigón entre fisuras y atravesado por armaduras como un hormigón debilitado,
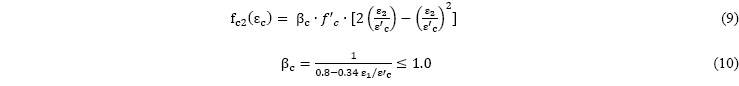
donde, ![]() es la deformación específica correspondiente al pico de la curva (como las normas ACI-318-11 [12] y CAN3-A23.3-04 [13] no especifican el valor de la deformación pico, su valor fue adoptado de Vecchio y Selby[14] como
es la deformación específica correspondiente al pico de la curva (como las normas ACI-318-11 [12] y CAN3-A23.3-04 [13] no especifican el valor de la deformación pico, su valor fue adoptado de Vecchio y Selby[14] como ![]() ). Para considerar los valores límites de las deformaciones principales, en este trabajo se adopta la deformación pico del hormigón debilitado
). Para considerar los valores límites de las deformaciones principales, en este trabajo se adopta la deformación pico del hormigón debilitado ![]() , ecuación (5).
, ecuación (5).
Se supone que ha ocurrido el aplastamiento de la biela cuando la compresión en la biela alcanza ![]() , donde
, donde ![]() es la resistencia pico de la curva tensión-deformación específica del ensayo del cilindro a compresión.
es la resistencia pico de la curva tensión-deformación específica del ensayo del cilindro a compresión.
Para la relación constitutiva del hormigón traccionado, después de que ocurre la fisuración diagonal ![]() (este modelo no considera la situación antes de la fisuración), la ecuación (11) presenta el valor de
(este modelo no considera la situación antes de la fisuración), la ecuación (11) presenta el valor de ![]() , donde
, donde ![]() puede ser considerado como un factor de debilitamiento de la resistencia a tracción del hormigón entre fisuras y
puede ser considerado como un factor de debilitamiento de la resistencia a tracción del hormigón entre fisuras y ![]() la resistencia a tracción simple del hormigón adoptada de Collins, et al.[10].
la resistencia a tracción simple del hormigón adoptada de Collins, et al.[10].
![]()
donde ![]() es la deformación correspondiente al inicio de la fisuración, con
es la deformación correspondiente al inicio de la fisuración, con ![]() el módulo de deformación tangente en el origen de la curva
el módulo de deformación tangente en el origen de la curva ![]() .
.
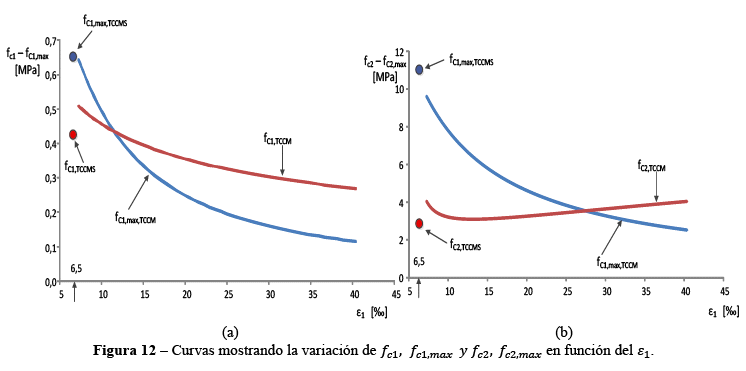
La ecuación (11) y Figura 12a muestran que la tensión principal de tracción entre las fisuras diagonales ![]() disminuye cuando los valores de
disminuye cuando los valores de ![]() aumentan.
aumentan.
Para elevados valores de ![]() , la armadura transversal sufre deformaciones excesivas (mayores a la deformación correspondiente al inicio de la fluencia, Figura 13b) y comienzan a ocurrir deslizamientos en la fisura. Las tensiones en el plano de la fisura, de fricción
, la armadura transversal sufre deformaciones excesivas (mayores a la deformación correspondiente al inicio de la fluencia, Figura 13b) y comienzan a ocurrir deslizamientos en la fisura. Las tensiones en el plano de la fisura, de fricción ![]() y tensiones normales de compresión
y tensiones normales de compresión ![]() se obtienen del análisis de la fisura, Figura 7.
se obtienen del análisis de la fisura, Figura 7.
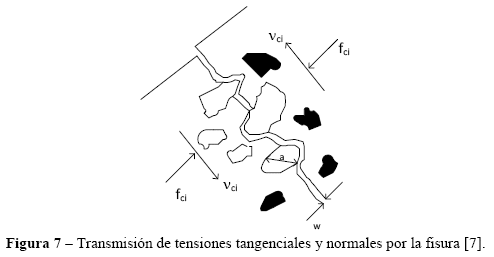
El estudio de la variación de tensiones en la fisura es importante porque muestra la capacidad última que podría soportar un elemento de membrana, las expresiones anteriores no consideran variaciones locales de tensiones. Si la deformación principal de tracción ![]() es elevada, la abertura de la fisura aumenta y el valor de la resistencia a la tracción disminuye rápidamente (Figura 12a y Figura 13a). Es necesario realizar un equilibrio de esfuerzos en la fisura que consideren variaciones locales de tensiones y deformaciones. La Figura 8 muestra las tensiones en las armaduras y en el hormigón para una sección entre dos fisuras (a) y en la fisura (b).
es elevada, la abertura de la fisura aumenta y el valor de la resistencia a la tracción disminuye rápidamente (Figura 12a y Figura 13a). Es necesario realizar un equilibrio de esfuerzos en la fisura que consideren variaciones locales de tensiones y deformaciones. La Figura 8 muestra las tensiones en las armaduras y en el hormigón para una sección entre dos fisuras (a) y en la fisura (b).
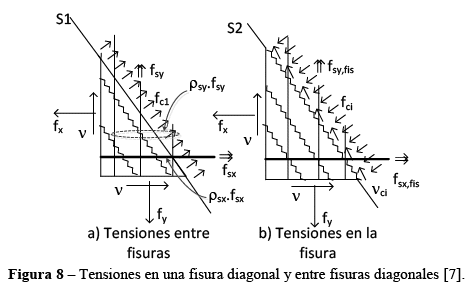
Considerando el equilibrio de las tensiones en las direcciones x y y de la Figura 8b (en la sección de la fisura) y asumiendo el área de las secciones S1 y S2 igual a la unidad y desconsiderando las tensiones normales de compresión en el plano de la fisura ![]() , Figuras 7 y 8, se obtiene:
, Figuras 7 y 8, se obtiene:
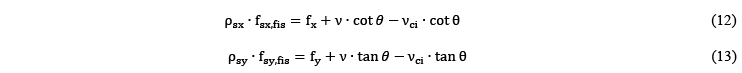
donde, ![]() las tensiones actuantes en el plano de la fisura en las armaduras en las direcciones x yy, respectivamente. En Vecchio y Collins [2] se demuestra que es necesaria la presencia de las tensiones
las tensiones actuantes en el plano de la fisura en las armaduras en las direcciones x yy, respectivamente. En Vecchio y Collins [2] se demuestra que es necesaria la presencia de las tensiones ![]() para el equilibrio del elemento de membrana.
para el equilibrio del elemento de membrana.
Resolviendo la ecuación(13) para la tensión tangencial ![]() y retirando la tensión normal
y retirando la tensión normal ![]() , por ser poco representativa en vigas, se obtiene la ecuación(14), donde
, por ser poco representativa en vigas, se obtiene la ecuación(14), donde ![]() depende de la tensión de fricción junto a la fisura
depende de la tensión de fricción junto a la fisura ![]() , Figura 7.
, Figura 7.
![]()
Comparando la ecuación (14) y la ecuación (8), se puede deducir que cuando la tensión de trabajo en la fisura alcanza la fluencia ![]() se tiene que
se tiene que ![]() , que según el modelo correspondería a una situación límite
, que según el modelo correspondería a una situación límite ![]() , cuando pueden ocurrir deslizamientos en la fisura, o sea, para que no ocurran deslizamientos en la fisura
, cuando pueden ocurrir deslizamientos en la fisura, o sea, para que no ocurran deslizamientos en la fisura ![]() ,
,
![]()
Según Walraven[1] apud Vecchio y Collins[2] las tensiones de fricción en la fisura se pueden adoptar como ![]() . A favor de la seguridad, sin considerar las tensiones normales
. A favor de la seguridad, sin considerar las tensiones normales ![]() , la ecuación (16)determina el valor de
, la ecuación (16)determina el valor de ![]() ,
,
![]()
Según Vecchio y Collins [2] la tensión de fricción máxima entre las fisuras puede ser adoptada como![]() ] y considerando las ecuaciones (15) y (16), la tensión de tracción límite entre las fisuras se puede escribir como
] y considerando las ecuaciones (15) y (16), la tensión de tracción límite entre las fisuras se puede escribir como ![]() (la Figura 12a muestra cómo disminuye el
(la Figura 12a muestra cómo disminuye el ![]() con el aumento de la deformación principal
con el aumento de la deformación principal ![]() y en la Figura 12b se muestra la disminución de
y en la Figura 12b se muestra la disminución de ![]() con el aumento de
con el aumento de ![]() ). El modelo no sirve para valores mayores a éste, la ecuación (17) muestra el valor de
). El modelo no sirve para valores mayores a éste, la ecuación (17) muestra el valor de ![]() ,
,

donde, a es el diámetro máximo del agregado en mm, ![]() es el ancho medio de la fisura diagonal en mm y
es el ancho medio de la fisura diagonal en mm y ![]() es la separación entre las fisuras diagonales que se obtiene de Vecchio y Collins [2] y que se muestra en la ecuación (18), ver Figuras 2 y 7,
es la separación entre las fisuras diagonales que se obtiene de Vecchio y Collins [2] y que se muestra en la ecuación (18), ver Figuras 2 y 7,
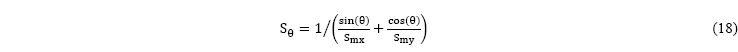
dónde, ![]() son las componentes de las separaciones medias entre las fisuras en dirección xyy, respectivamente, y pueden ser calculadas con (adaptadas de Kaufmann[6]):
son las componentes de las separaciones medias entre las fisuras en dirección xyy, respectivamente, y pueden ser calculadas con (adaptadas de Kaufmann[6]):
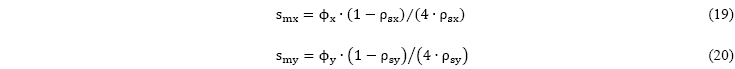
dónde ![]() , son los diámetros de la armaduras en relación a la dirección x y y, respectivamente.
, son los diámetros de la armaduras en relación a la dirección x y y, respectivamente.
Para resolver todos los parámetros de la TCCM son necesarias muchas interacciones y se plantean 15 ecuaciones que se muestran en la Figura 2 de Bentz, Vecchio y Collins[3]. En total son 23 pasos (Vecchio y Collins[2]), entre los cuales se comienzan adoptando parámetros relacionados a las fisuras, se estima el ángulo de inclinación de las fisuras diagonales, se estiman tensiones de trabajo de las armaduras y luego se comienzan resolviendo las ecuaciones de equilibrio y se calculan las deformaciones específicas en las direcciones de los ejes x y y. Con el valor de éstas, se verifica si las tensiones de trabajo adoptadas corresponden a las estimadas, si no corresponde se vuelven a estimar valores hasta que cierren las interacciones y se alcance alguno de los estados límites (EL). Se considera falla (EL) cuando: 1) ![]() , ocurrió un deslizamiento en la fisura; 2)
, ocurrió un deslizamiento en la fisura; 2) ![]() , ocurrió el aplastamiento de la biela comprimida y 3)
, ocurrió el aplastamiento de la biela comprimida y 3) ![]() , ocurrió la fluencia de la armadura longitudinal.
, ocurrió la fluencia de la armadura longitudinal.
Posteriormente en Collins, et al.[10], se define el Método General de Dimensionamiento a Esfuerzos Cortantes ordenando mejor el modelo, la norma canadiense CAN23.3-94 [15] la adopta como un modelo alternativo de dimensionamiento de elementos de hormigón armado sujetos a esfuerzos cortantes. En este modelo se considera ![]() en la posición del centroide de la armadura longitudinal traccionada y el aporte del hormigón en la resistencia al cortante se define como
en la posición del centroide de la armadura longitudinal traccionada y el aporte del hormigón en la resistencia al cortante se define como ![]() que se obtiene de la ecuación (8). Las expresiones de la TCCM permanecen, quedando
que se obtiene de la ecuación (8). Las expresiones de la TCCM permanecen, quedando ![]() a ser encontrados en forma interactiva (en realidad el factor de debilitamiento del hormigón comprimido y traccionado
a ser encontrados en forma interactiva (en realidad el factor de debilitamiento del hormigón comprimido y traccionado ![]() y
y ![]() ).
).
Para que puedan aplicarse ambos modelos son necesarias varias interacciones, y el resultado final nos permite obtener los parámetros de diseño ![]()
En vigas sujetas, por ejemplo, a cargas uniformes donde los tramos de vigas tienen esfuerzos cortantes y momentos flectores, existe una variación linear de los esfuerzos cortantes. Los resultados obtenidos por los paneles sujetos a cortante puro o cortante combinado con esfuerzos axiales con armaduras uniformemente distribuidas en direcciones x yy, no corresponden totalmente a estos tipos de elementos. Como las tensiones de trabajo y las deformaciones específicas de los estribos dependen del valor de los esfuerzos cortantes, sus valores serán diferentes en cada estribo y a lo largo de su altura. Para considerar esta situación es necesario realizar un análisis no linear físico de la viga, discretizando el alma de la misma con elementos de membrana en diferentes posiciones, considerando su posición real de cada elemento en la viga.
6. MÉTODO SIMPLIFICADO DEL TCCM
Considerando los motivos descritos en el último párrafo del ítem anterior y la necesidad de que los proyectistas puedan encontrar resultados rápidamente y con significados físicos. Bentz, Vecchio y Collins[3] han estudiado un modelo simplificado eliminando la necesidad de interacciones. En este modelo simplificado se asume que ![]() y
y ![]() (Figura 8) serán iguales a la tensión de fluencia
(Figura 8) serán iguales a la tensión de fluencia ![]() (se asume que las deformaciones en las armaduras serán mayores a la deformación que corresponde al inicio de la fluencia
(se asume que las deformaciones en las armaduras serán mayores a la deformación que corresponde al inicio de la fluencia ![]() ) y tensiones normales verticales nulas
) y tensiones normales verticales nulas ![]() (poco representativas). La ecuación (21) muestra el equilibrio entre las tensiones tangenciales
(poco representativas). La ecuación (21) muestra el equilibrio entre las tensiones tangenciales ![]() y las tensiones en las fisuras de la sección S2 en la Figura 8 (desconsiderando las tensiones normales de compresión, Figura 7), ver también la ecuación (13),
y las tensiones en las fisuras de la sección S2 en la Figura 8 (desconsiderando las tensiones normales de compresión, Figura 7), ver también la ecuación (13),
![]()
De la misma forma, de la segunda ecuación de equilibrio (7), con las simplificaciones ya mencionadas en el anterior párrafo, se tiene:
![]()
Las ecuaciones (21) y (22)se pueden expresar como:
![]()
Para secciones con armaduras longitudinales y transversales, el modelo TCCMS asume las siguientes expresiones simplificadas para encontrar directamente el valor de la inclinación de las tensiones principales de compresión ![]() , ecuación (24), y para el factor de debilitamiento del hormigón entre fisuras
, ecuación (24), y para el factor de debilitamiento del hormigón entre fisuras ![]() , ecuación (25):
, ecuación (25):
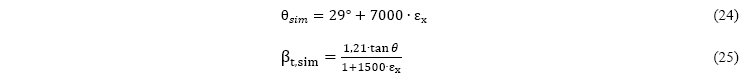
El trabajo de Bentz, Vecchio y Collins [3] presenta muchas expresiones para elementos estructurales sin armadura transversal (SAT), que en este caso no son analizados por no estar dentro de los objetivos directos del estudio. Pero, por ejemplo, las expresiones simplificadas para ![]() en elementos sin armadura transversal se presentan en las ecuaciones (26) y (27):
en elementos sin armadura transversal se presentan en las ecuaciones (26) y (27):
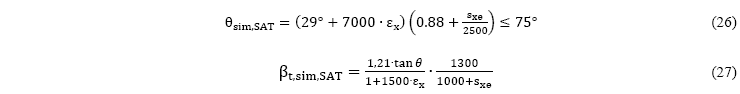
donde ![]() es un parámetro de la componente horizontal efectiva de la separación entre fisuras diagonales y
es un parámetro de la componente horizontal efectiva de la separación entre fisuras diagonales y ![]() , en la TCCD es la componente horizontal de la separación entre fisuras diagonales y en este modelo (sin armadura transversal), se permite considerar como separación vertical entre armaduras longitudinales.
, en la TCCD es la componente horizontal de la separación entre fisuras diagonales y en este modelo (sin armadura transversal), se permite considerar como separación vertical entre armaduras longitudinales.
La norma CAN3-A23.3-04[13] ya incluye el modelo simplificado de la TCCM y lo adopta como su método general en el dimensionamiento de elementos estructurales sujetos a esfuerzos cortantes pero,en su modelo simplificado, sugiere adoptar, para hormigones con ![]() y resistencia de la armadura longitudinal
y resistencia de la armadura longitudinal ![]() :
: ![]() .
.
Está claro que al acercarse la falla en la armadura transversal, el ángulo ![]() disminuye y las armaduras transversales estarán trabajando con su capacidad máxima, aumentado el aporte de
disminuye y las armaduras transversales estarán trabajando con su capacidad máxima, aumentado el aporte de ![]() . Al ocurrir esto,
. Al ocurrir esto, ![]() aumenta con la consecuente disminución del aporte del hormigón en la resistencia al cortante
aumenta con la consecuente disminución del aporte del hormigón en la resistencia al cortante ![]() . Las ecuaciones(8) y (23) muestran estos aportes.
. Las ecuaciones(8) y (23) muestran estos aportes.
Bentz, Vecchio y Collins[3] han verificado también que una gran disminución de ![]() también provocará un aumento en el esfuerzo de la armadura longitudinal.
también provocará un aumento en el esfuerzo de la armadura longitudinal.
Una forma de adoptar ![]() en el modelo TCCMS, es considerar para qué valor de
en el modelo TCCMS, es considerar para qué valor de ![]() se tendrá la máxima contribución del hormigón
se tendrá la máxima contribución del hormigón ![]() . Con las ecuaciones (23), (24) y (25) se obtiene la resistencia a las tensiones tangenciales del elemento, pero también son necesarias interacciones para ajustar el valor de
. Con las ecuaciones (23), (24) y (25) se obtiene la resistencia a las tensiones tangenciales del elemento, pero también son necesarias interacciones para ajustar el valor de ![]() adoptado (en la TCCMS,
adoptado (en la TCCMS, ![]() corresponde a la deformación a media altura de la viga). Lo interesante del modelo es que no permite que la armadura longitudinal alcance la fluencia (pero a media altura de la viga). Otros estudios presentan tablas en lugar de interacciones como en AASHTO, LRFD[8].
corresponde a la deformación a media altura de la viga). Lo interesante del modelo es que no permite que la armadura longitudinal alcance la fluencia (pero a media altura de la viga). Otros estudios presentan tablas en lugar de interacciones como en AASHTO, LRFD[8].
La norma ACI[12] para flexión simple y cortante mantiene por casi 50 años ![]() (o
(o ![]() ) constante para cualquier
) constante para cualquier ![]() (tiene una expresión alternativa
(tiene una expresión alternativa![]() , donde
, donde ![]() es la cuantía de armadura longitudinal traccionada, d la altura útil y
es la cuantía de armadura longitudinal traccionada, d la altura útil y ![]() esfuerzos actuantes en la sección, esta expresión alternativa es muy poco utilizada). Este valor de
esfuerzos actuantes en la sección, esta expresión alternativa es muy poco utilizada). Este valor de ![]() de la ACI corresponde supuestamente al valor de la tensión tangencial de formación de fisuras diagonales.
de la ACI corresponde supuestamente al valor de la tensión tangencial de formación de fisuras diagonales.
Expresiones simples de ![]() ya fueron eliminadas por otros códigos desde hace mucho tiempo, por ejemplo hace casi 25 años el CEB-FIP 90 [16] tiene una expresión más refinada. La norma CBH-87[17] tiene una expresión corta como de la ACI, que tampoco depende de
ya fueron eliminadas por otros códigos desde hace mucho tiempo, por ejemplo hace casi 25 años el CEB-FIP 90 [16] tiene una expresión más refinada. La norma CBH-87[17] tiene una expresión corta como de la ACI, que tampoco depende de ![]() , pero su resultado parece muy elevado.
, pero su resultado parece muy elevado.
En el estudio de paneles fisurados Vecchio [11] ha presentado otro modelo, el Modelo del Campo de Tensiones Disturbadas (MCTD), donde se demuestra que para algunas situaciones de armado la inclinación de las tensiones principales y deformaciones principales no es la misma, además ese modelo permite el deslizamiento en la fisura diagonal e incluye modificaciones en las ecuaciones constitutivas del hormigón fisurado comprimido y traccionado.
Cabe distinguir que en elementos con esfuerzos predominantes de flexión, como en el caso de vigas, en las verificaciones en el Estado Límite Último (ELU), las armaduras longitudinales se diseñan para que trabajen en la fluencia pero en situaciones de servicio usualmente se encuentran dentro de las regiones elásticas.
7. APLICACIÓN PRÁCTICA
En esta aplicación será analizada una sección sujeta a momentos flectores, esfuerzos normales y esfuerzos cortantes, el diseño será integrado, pero serán obtenidas solamente armaduras transversales. Para su diseño será utilizada la norma ACI [12], con comparaciones con la norma canadiense CSA[13]. Se realizarán también comparaciones con los modelos de la TCCM y TCCMS.
Las normas ACI y CSA para el cálculo de sus materiales adoptan el bloque rectangular de tensiones simplificado. La Figura 9 muestra una sección rectangular con la nomenclatura y parámetros de diseño utilizados en el ejemplo. Se ha trabajado con los límites impuestos por la norma como ser sección controlada por tracción, entre otros (Aguirre[18]). Aguirre[7] y Aguirre[19] han utilizado diagramas realistas y para obtener el equilibrio de la sección frente a esfuerzos, en estos modelos se ha recurrido a la integración numérica para obtener la resultante del hormigón comprimido.
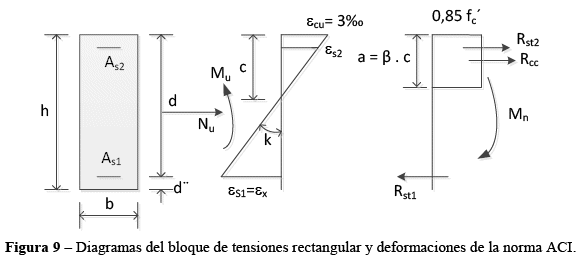
Desde Aguirre [7] se ha trabajado con un modelo donde el valor de ![]() se obtiene de la configuración de ruptura de la viga que equilibra los momentos flectores y esfuerzos axiales, de esta manera se evitan las interacciones y el valor de
se obtiene de la configuración de ruptura de la viga que equilibra los momentos flectores y esfuerzos axiales, de esta manera se evitan las interacciones y el valor de ![]() se obtiene analizando la posibilidad de deslizamiento de la fisura diagonal
se obtiene analizando la posibilidad de deslizamiento de la fisura diagonal ![]() (indirectamente la deformación de la armadura transversal
(indirectamente la deformación de la armadura transversal ![]() ) y la posibilidad del aplastamiento de la biela comprimida (
) y la posibilidad del aplastamiento de la biela comprimida (![]() ).
).
En este estudio, como se está trabajando en el ELU, para evitar la abertura de fisuras diagonales excesivas se ha definido que ![]() .
.
En la mayoría de las normas no existe la limitación de ![]() , solo la limitación de la tensión de trabajo máxima de la armadura transversal que indirectamente limita la deformación
, solo la limitación de la tensión de trabajo máxima de la armadura transversal que indirectamente limita la deformación ![]() . En el modelo propuesto es posible saber cuál es la deformación de la armadura transversal. Las normas CEB-FIP 90[16], CBH-87[17], EUROCODE 2[20] entre otras, establecen una deformación límite para la armadura longitudinal
. En el modelo propuesto es posible saber cuál es la deformación de la armadura transversal. Las normas CEB-FIP 90[16], CBH-87[17], EUROCODE 2[20] entre otras, establecen una deformación límite para la armadura longitudinal ![]() (la norma ACI no establece un límite).
(la norma ACI no establece un límite).
Con la ![]() de la sección de análisis 2 en la Figura 1, se puede obtener la tensión en la biela comprimida
de la sección de análisis 2 en la Figura 1, se puede obtener la tensión en la biela comprimida ![]() , considerando estribos verticales (
, considerando estribos verticales (![]() ).
).
Como el modelo propuesto tiene lineamientos de la TCCM, es necesario verificar el deslizamiento en la fisura ![]() y el aplastamiento de la biela comprimida, comparando la tensión actuante en la biela con
y el aplastamiento de la biela comprimida, comparando la tensión actuante en la biela con ![]() . Se obtiene otros parámetros como el factor de debilitamiento del hormigón comprimido y traccionado, etc.
. Se obtiene otros parámetros como el factor de debilitamiento del hormigón comprimido y traccionado, etc.
La teoría descrita anteriormente se aplica al dimensionamiento de los estribos para una viga con sección rectangular de 20 cm x 40 cm, sujeta a los siguientes esfuerzos últimos: ![]() . Los materiales son
. Los materiales son ![]() . Para calcular algunos parámetros relacionados con las fisuras, fueron adoptados los siguientes datos: diámetro de la armadura longitudinal 12 mm, diámetro de la armadura transversal 10 mm, diámetro máximo del agregado 25 mm, cuantía de armadura longitudinal
. Para calcular algunos parámetros relacionados con las fisuras, fueron adoptados los siguientes datos: diámetro de la armadura longitudinal 12 mm, diámetro de la armadura transversal 10 mm, diámetro máximo del agregado 25 mm, cuantía de armadura longitudinal ![]() y cuantía de armadura transversal
y cuantía de armadura transversal ![]() .Para la elaboración de las rutinas fue empleado el programa algébrico y simbólico Mathcad.
.Para la elaboración de las rutinas fue empleado el programa algébrico y simbólico Mathcad.
Ambos métodos (TCCM y TCCMS) fueron adecuados a los parámetros de diseño de la norma CSA [13], con las consideraciones del modelo de este trabajo. Con los datos del problema fue encontrada la configuración de ruptura de la sección en estudio y se obtuvo para la deformación de la armadura traccionada ![]() .
.
La norma ACI [12] aplica un solo factor ![]() sobre el esfuerzo cortante resistente (suma del aporte del hormigón y de la armadura transversal) y la norma CSA [13] aplica dos factores,
sobre el esfuerzo cortante resistente (suma del aporte del hormigón y de la armadura transversal) y la norma CSA [13] aplica dos factores,![]() sobre el aporte del hormigón y
sobre el aporte del hormigón y ![]() sobre el aporte de la armadura.
sobre el aporte de la armadura.
La Tabla 1 presenta los resultados de la TCCM y del modelo de este trabajo con las tentativas realizadas para diversos valores de ![]() (la variación de
(la variación de ![]() ha sido de 1º y se ha variado desde 25º hasta 65º, los valores extremos e intermedios que no interesan no se muestran) y sus parámetros de diseño correspondientes. En este caso, el criterio para escoger el ángulo
ha sido de 1º y se ha variado desde 25º hasta 65º, los valores extremos e intermedios que no interesan no se muestran) y sus parámetros de diseño correspondientes. En este caso, el criterio para escoger el ángulo ![]() ha sido de verificar que la biela no aplaste y no ocurra del deslizamiento en la fisura. Se ha marcado los parámetros que corresponden al ángulo escogido.
ha sido de verificar que la biela no aplaste y no ocurra del deslizamiento en la fisura. Se ha marcado los parámetros que corresponden al ángulo escogido.
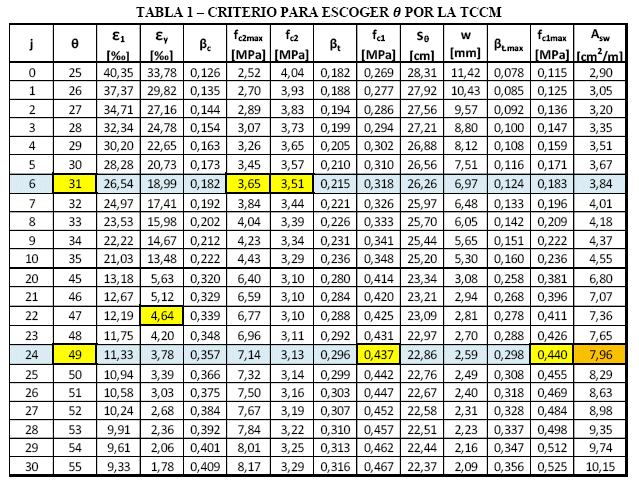
Inicialmente, comparando el aplastamiento del hormigón, se verifica que el hormigón aplasta para ![]() (la Figura 11a también muestra esta conclusión). Analizando el deslizamiento, para
(la Figura 11a también muestra esta conclusión). Analizando el deslizamiento, para ![]() existe deslizamiento, significa que
existe deslizamiento, significa que ![]() , la Figura 14a y la Tabla 1 muestran que a mayor ángulo mayor es la cantidad de armadura, luego se ha adoptado
, la Figura 14a y la Tabla 1 muestran que a mayor ángulo mayor es la cantidad de armadura, luego se ha adoptado ![]() y para este ángulo se ha obtenido una armadura transversal por unidad de longitud de:
y para este ángulo se ha obtenido una armadura transversal por unidad de longitud de: ![]() .
.
En esta misma Tabla 1 se verifica otros parámetros para ![]() como la deformación del estribo
como la deformación del estribo ![]() , mayor que la deformación del inicio de la fluencia y menor al límite establecido en este trabajo de
, mayor que la deformación del inicio de la fluencia y menor al límite establecido en este trabajo de ![]() . Se asume que para deformaciones específicas mayores que
. Se asume que para deformaciones específicas mayores que ![]() ocurrirá el deslizamiento de los agregados en la fisura diagonal. La abertura de la fisura diagonal
ocurrirá el deslizamiento de los agregados en la fisura diagonal. La abertura de la fisura diagonal ![]() corresponde a una situación de un EL, no corresponde un estado límite de servicio (ELS).
corresponde a una situación de un EL, no corresponde un estado límite de servicio (ELS).
En la Tabla 2 se muestra para el ángulo ![]() de la TCCMS y cuáles son los parámetros de diseño encontrados. En este caso
de la TCCMS y cuáles son los parámetros de diseño encontrados. En este caso ![]() , pero corresponde a la deformación de la mitad de la altura de la sección.
, pero corresponde a la deformación de la mitad de la altura de la sección.

En esta Tabla 2 se obtiene ![]() con la ecuación (24) (sin necesidad de interacciones), en este modelo y para este ángulo no se tiene aplastamiento de la biela y tampoco existe deslizamiento en la fisura diagonal y todos sus otros parámetros se encuentran dentro de valores razonables (ver también Figuras 11a y 11b).
con la ecuación (24) (sin necesidad de interacciones), en este modelo y para este ángulo no se tiene aplastamiento de la biela y tampoco existe deslizamiento en la fisura diagonal y todos sus otros parámetros se encuentran dentro de valores razonables (ver también Figuras 11a y 11b).
Finalmente, la Tabla 3 muestra un resumen del área de las armaduras transversales obtenidas por la TCCM, TCCMS, y las normas ACI-318M-11[12] y CAN3-A23.3-04[13]indicando los aportes del hormigón, de la armadura transversal y otros importantes parámetros de diseño.
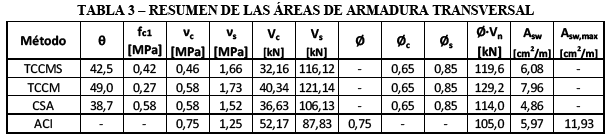
En la Tabla 3 se verifica que existe variación en los resultados de las armaduras, esto es porque los modelos son calibrados de forma diferente, por ejemplo, para obtener el ![]() por la CSA y la TCCMS se utiliza la misma ecuación (24), pero el valor de la deformación longitudinal a media altura de la sección
por la CSA y la TCCMS se utiliza la misma ecuación (24), pero el valor de la deformación longitudinal a media altura de la sección ![]() es diferente (
es diferente (![]() , esto provoca resultados diferentes.
, esto provoca resultados diferentes.
En la misma Tabla 3, se observa que para la norma ACI existe un límite de armadura transversal máxima, es una forma indirecta de verificar el aplastamiento de la biela comprimida. También no define el ángulo ![]() , pero se asume que es
, pero se asume que es ![]() porque en sus expresiones de los aportes del hormigón y de la armadura en la resistencia al cortante no explicita
porque en sus expresiones de los aportes del hormigón y de la armadura en la resistencia al cortante no explicita ![]() . Las expresiones de la CSA tienen
. Las expresiones de la CSA tienen ![]() y los modelos TCCM y TCCMS también, ecuaciones (8) y (23).
y los modelos TCCM y TCCMS también, ecuaciones (8) y (23).
Para ver la variación de los diferentes parámetros de diseño, se han graficado unas curvas comparando los modelos de la TCCM y TCCMS, estas curvas se muestran en las Figuras 10 hasta la Figura 14.
Existe una relación inversa entre ![]() y las deformaciones específicas
y las deformaciones específicas ![]() . Para
. Para ![]() pequeños, la Figura 10a manifiesta deformaciones excesivas de las armaduras transversales y la Figura 10b deformaciones principales medias excesivas, que significa aberturas de fisuras diagonales excesivas para
pequeños, la Figura 10a manifiesta deformaciones excesivas de las armaduras transversales y la Figura 10b deformaciones principales medias excesivas, que significa aberturas de fisuras diagonales excesivas para ![]() pequeños. En las Figuras 10a y 10b están marcados los valores de las deformaciones específicas para el ángulo
pequeños. En las Figuras 10a y 10b están marcados los valores de las deformaciones específicas para el ángulo ![]() adoptado y dónde se situarían los valores que corresponden a TCCMS.
adoptado y dónde se situarían los valores que corresponden a TCCMS.

En las Figuras 11a y 11b se muestran las tensiones principales ![]() en función de
en función de ![]() , se comprueba que para
, se comprueba que para ![]() ocurrirá aplastamiento de las bielas comprimidas (Figura 11a) y que para
ocurrirá aplastamiento de las bielas comprimidas (Figura 11a) y que para ![]() puede ocurrir un deslizamiento en las fisuras diagonales (Figura 11b), en ambos casos se enseñan los valores máximos y de trabajo para el
puede ocurrir un deslizamiento en las fisuras diagonales (Figura 11b), en ambos casos se enseñan los valores máximos y de trabajo para el ![]() adoptado. También están indicados los valores correspondientes al modelo TCCMS donde se verifica que en ambas situaciones no está ocurriendo un EL.
adoptado. También están indicados los valores correspondientes al modelo TCCMS donde se verifica que en ambas situaciones no está ocurriendo un EL.

En la Figura 12a y 12b, se verifica la influencia de la deformación específica principal ![]() en el valor de las tensiones principales
en el valor de las tensiones principales ![]() y sobre sus máximas correspondientes
y sobre sus máximas correspondientes ![]() , donde se intersectan las curvas a la deformación
, donde se intersectan las curvas a la deformación ![]() límite, siendo que el límite para ambas figuras es del deslizamiento en la fisura diagonal o sea
límite, siendo que el límite para ambas figuras es del deslizamiento en la fisura diagonal o sea ![]() , Tabla 1 y Figura 12a. En estas figuras también se muestran los valores correspondientes a la TCCMS.
, Tabla 1 y Figura 12a. En estas figuras también se muestran los valores correspondientes a la TCCMS.
La Figura 13a destaca la relación directa que existe entre la abertura de fisuras diagonales ![]() y la deformación específica principal
y la deformación específica principal ![]() , esto se aplica en todas las relaciones donde interviene
, esto se aplica en todas las relaciones donde interviene ![]() . Por ejemplo en el caso de las Figuras 12a y 12b las tensiones principales actuantes y máximas disminuyen al aumentar la abertura de sus fisuras diagonales, que en el caso del ángulo
. Por ejemplo en el caso de las Figuras 12a y 12b las tensiones principales actuantes y máximas disminuyen al aumentar la abertura de sus fisuras diagonales, que en el caso del ángulo ![]() la abertura de la fisura es
la abertura de la fisura es ![]() que corresponde al EL del deslizamiento en la fisura (Tabla 1).
que corresponde al EL del deslizamiento en la fisura (Tabla 1).
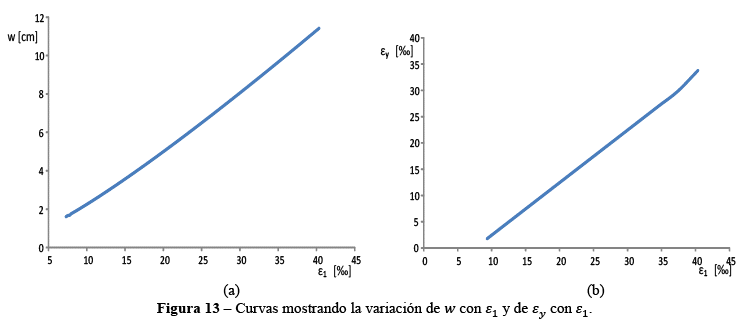
Para el caso de la Figura 13b, existe una relación directa entre ![]() y la deformación específica del estribo
y la deformación específica del estribo ![]() , y como se quiere evitar aberturas de fisuras diagonales excesivas es necesario limitar el valor de
, y como se quiere evitar aberturas de fisuras diagonales excesivas es necesario limitar el valor de ![]() (en este trabajo a 5). Normalmente, las normas no establecen un valor límite para
(en este trabajo a 5). Normalmente, las normas no establecen un valor límite para ![]() , pero limitan el valor de la tensión de trabajo de la armadura transversal.
, pero limitan el valor de la tensión de trabajo de la armadura transversal.
La Figura 14a refleja un incremento del valor de la armadura transversal ![]() al aumentar
al aumentar ![]() , significa que sería más económico adoptar valores de
, significa que sería más económico adoptar valores de ![]() pequeños, pero en este caso se tendría aplastamiento de la biela comprimida o deslizamiento en la fisura diagonal. Para cumplir ambas situaciones su valor como mínimo debe ser
pequeños, pero en este caso se tendría aplastamiento de la biela comprimida o deslizamiento en la fisura diagonal. Para cumplir ambas situaciones su valor como mínimo debe ser ![]() , podría adoptarse valores mayores a este pero sería antieconómico.
, podría adoptarse valores mayores a este pero sería antieconómico.
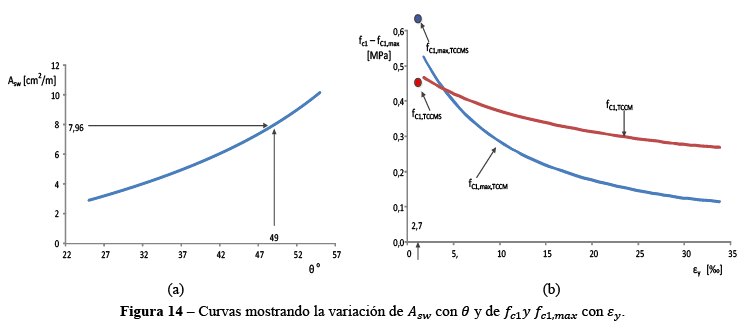
La Figura 14b indica la variación de las tensiones principales de tracción ![]() con la deformación de la armadura transversal
con la deformación de la armadura transversal![]() , se puede apreciar que sólo para deformaciones transversales pequeñas no se tendría deslizamientos en la fisura. En la misma figura, se verifica que para la TCCMS
, se puede apreciar que sólo para deformaciones transversales pequeñas no se tendría deslizamientos en la fisura. En la misma figura, se verifica que para la TCCMS ![]() y para este valor no existe deslizamiento en la fisura diagonal.
y para este valor no existe deslizamiento en la fisura diagonal.
8. CONCLUSIONES
La TCCM le da un significado físico al dimensionamiento de elementos sujetos a esfuerzos cortantes. En la TCCM existe un modelo que explica los parámetros utilizados en el dimensionamiento en base a ecuaciones de equilibrio, a compatibilidad de deformaciones y en base a ecuaciones constitutivas que fueron obtenidas de ensayos de laboratorio. Se ha verificado que existe una tensión de tracción entre fisuras ![]() que es perpendicular a las fisuras diagonales que es incorporada en el modelo para calcular el aporte del hormigón en la resistencia al cortante, contradiciendo a las teorías del cálculo de secciones de hormigón armado, en las cuales casi nunca consideran la resistencia a tracción del hormigón. Surgen 2 parámetros importantes que son factores que ponderan la resistencia a compresión
que es perpendicular a las fisuras diagonales que es incorporada en el modelo para calcular el aporte del hormigón en la resistencia al cortante, contradiciendo a las teorías del cálculo de secciones de hormigón armado, en las cuales casi nunca consideran la resistencia a tracción del hormigón. Surgen 2 parámetros importantes que son factores que ponderan la resistencia a compresión ![]() y tracción
y tracción ![]() del hormigón fisurado, tratando al hormigón fisurado como un nuevo material. Estos parámetros están en función de la abertura de las fisuras diagonales
del hormigón fisurado, tratando al hormigón fisurado como un nuevo material. Estos parámetros están en función de la abertura de las fisuras diagonales ![]() y de la deformación longitudinal
y de la deformación longitudinal ![]() . También se explica que a mayor deformación longitudinal, menores serán los aportes resistentes del hormigón armado al esfuerzo cortante (relación directa entre
. También se explica que a mayor deformación longitudinal, menores serán los aportes resistentes del hormigón armado al esfuerzo cortante (relación directa entre ![]() , ecuación (5)). El problema de la TCCM es que tiene muchas interacciones en la obtención de sus parámetros.
, ecuación (5)). El problema de la TCCM es que tiene muchas interacciones en la obtención de sus parámetros.
Las armaduras encontradas por el método modificado, simplificado, la norma ACI y la norma canadiense, en algunos casos tienen proximidad en sus resultados, pero las diferencias son producto de los diferentes parámetros que adoptan sus modelos, en éstos el ángulo ![]() , los modelos que tienen mayor ángulo tienen cuantías de armadura mayor, que es lo que se ha verificado en la Figura 14a. Para la norma ACI, como se asume
, los modelos que tienen mayor ángulo tienen cuantías de armadura mayor, que es lo que se ha verificado en la Figura 14a. Para la norma ACI, como se asume ![]() , la cuantía de armadura encontrada corresponde aproximadamente a este ángulo. Con la TCCM y TCCMS es posible conocer la deformación de la armadura transversal, que resulta en mayor confiabilidad en la cuantía de armadura obtenida. También se ha verificado que con estos modelos se obtiene mayor cantidad de armadura transversal. Los resultados muestran variabilidad en las cuantías de armadura, que significa que es necesario mayores investigaciones, por ejemplo, con modelos numéricos que consideren no linealidades físicas y mecánica de la fractura contrastando con resultados de más ensayos de laboratorio.
, la cuantía de armadura encontrada corresponde aproximadamente a este ángulo. Con la TCCM y TCCMS es posible conocer la deformación de la armadura transversal, que resulta en mayor confiabilidad en la cuantía de armadura obtenida. También se ha verificado que con estos modelos se obtiene mayor cantidad de armadura transversal. Los resultados muestran variabilidad en las cuantías de armadura, que significa que es necesario mayores investigaciones, por ejemplo, con modelos numéricos que consideren no linealidades físicas y mecánica de la fractura contrastando con resultados de más ensayos de laboratorio.
9. BIBLIOGRAFÍA
[1] M. P. Collins. Towards a Rational Theory for RC Memebers in Shear, Proccedings. Journal of Structural Division - ASCE, vol. 104, no. 4, pp. 649-666, April 1978.
[2] F. J. Vecchio and M. P. Collins. The Modified Compression- Field Theory for Reinforced Concrete Elements Subjected to Shear. ACI Structural Journal, vol. 83, no. 2, pp. 219-231, March-April 1986.
[3] E. C. Bentz et al. Simplified Modified Compression Field Theory for Calculating Shear Strength of Reinforced Concrete Elements. ACI Structural Journal, vol. 103, no. 4, pp. 614-624, July – August – 2006.
[4] M. P. Collins et al. An Adequate Theory for the Shear Strenght of Reinforced Concrete Structures, in Morley Symposium on Concrete Plasticity and its aplication. University of Cambridge, July 2007, pp. 75-94.
[5] M. P. Collins et al. Where is shear reinforment required? Review of Research Results and Design Procedures. ACI Structural Journal, vol. 105, no. 5, pp. 590-600, September-October 2008.
[6] W. Kaufmann. Analysis of RC Membranes in Design Practice, in: Fib Symposium Prague, Proceeding, Prague, pp. 5, 1999.
[7] F. Aguirre. Dimensionamiento Integrado de Secciones sujetas a momentos flectores y esfuerzos cortantes para concretos de alta Resistencia. Investigación & Desarrollo, Universidad Privada Boliviana, vol. 10, pp. 67-80, Marzo 2010.
[8] AASHTO, LRFD Bridge Design Specifications and Comentary, 3er edition, American Association of State Highway and Transportation Officials, Washington, DC, 2004.
[9] S. P. Timoshenko and J. N. Goodier. Theory of Elasticity. Tokyo: McGraw-Hill, 1970.
[10] M. P. Collins et al. A General Shear Design. ACI Structural Journal, vol. 93, no. 1, , pp. 36-45, January – February 1996.
[11] F.J. Vecchio. Disturbed Stress Field Model for Reinforced Concrete Structures. ASCE, Journal of Structural Engineering, vol. 126, no. 9, , pp. 1070-1077, September – 2000.
[12] AMERICAN CONCRETE INSTITUTE, Building Code Requirements for Structural Concrete, ACI-318M-11, ACI Committee 318, September 2011. [ Links ]
[13] STANDARDS COUNCIL OF CANADA, Design on Concrete Structures of Buildings, CAN3-A23.3-04, Canadian Standard Association, Canada, 2004.
[14] P.J. Vecchio and R.G. Selby. A constitutive model for analysis of reinforced concrete solids. Candian Journal of Civil Engineering, vol. 24, pp. 460-470, 1997.
[15] STANDARDS COUNCIL OF CANADA, Design on Concrete Structures of Buildings, CAN3-A23.3-94. Canadian Standard Association, Canada, 1994.
[16] CEB-FIP. Model Code For Concrete Structures, MC 90. Comité Euro-International du Béton, Thomas Telford Services Ltd., Switzerland, 1993.
[17] MINISTERIO DE URBANISMO Y VIVIENDA, Norma Boliviana del Hormigón Armado, CBH-87, La Paz, 1987. [ Links ]
[18] F. Aguirre. Texto de clases de Hormigón Armado, Universidad Privada Boliviana, 2014. [ Links ]
[19] F. Aguirre. Axial Load Moment Interaction Charts for High Performance Concrete. Investigación & Desarrollo, Universidad Privada Boliviana, vol. 3, , pp 23-34, Junio-2003.
[20] EUROPEAN COMMITTEE FOR STANDARDIZATION, STANDAR EN 1992-1-1:2004, Design of Concrete Structures – Part 1-1General Rules ans Rules for Buildings, EUROCODE 2 (2004), Brussels, 2004. [ Links ]
[21] F. J. Vecchio and M.P. Collins. Members ASCE, Compression Response of Cracked Reinforced Concrete. Journal of Structural Engineering, vol. 119, no. 12, pp. 3590-3610, December 1993.
[22] ASCE-ACI COMMITTE 445 ON SHEAR AN Torsion, Recent Approaches to Shear Design of Structural Concrete, Journal of Structural Engineering, 124(12), December 1998, pp. 1375-1417. [ Links ]
NOTAS
[1]Walraven, J.C.,Fundamental Analysis of Aggregate Interlock, ASCE, v.107, ST11, November 1981.














