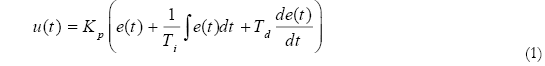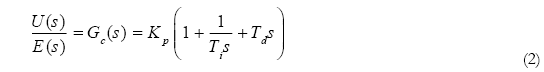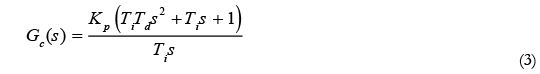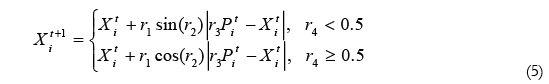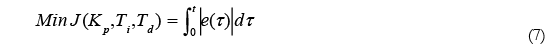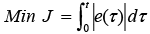Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1 Introducción
Durante las últimas décadas, las técnicas de control de procesos en la industria han tenido grandes avances, se han estudiado numerosos métodos de control, como el control adaptativo, el control neuronal y el control difuso; entre ellos, el más popular es el controlador PID (Proporcional Integral-Derivativo), que es ampliamente utilizado en la industria debido a su estructura simple y desempeño robusto en una amplia gama de condiciones de operación (2).
Desafortunadamente, ha sido bastante difícil ajustar las ganancias de los controladores PID porque muchas plantas industriales a menudo se ven abrumadas por problemas como orden alto, retrasos de tiempo y no linealidades (4). A lo largo de los años, se han propuesto varios métodos heurísticos para la sintonización de controladores PID y modificaciones a su estructura básica (1, 3).
En este sentido, técnicas de optimización permiten encontrar la mejor solución posible para un determinado problema y por ende valores óptimos para maximizar o minimizar una determinada salida pueden ser determinados. La gran mayoría de los problemas de optimización con implicaciones prácticas en la ciencia, la ingeniería, la economía y los negocios son muy complejos y difíciles de resolver. Dichos problemas no pueden resolverse de manera exacta utilizando métodos de optimización clásicos, entonces bajo estas circunstancias, los métodos de algoritmos meta heurísticos se han establecido como una solución alternativa tal como el Algoritmo Seno-Coseno introducido por Mirjalili (5), el cual será empleado en el presente trabajo para sintonizar las ganancias de un controlador PID como parte de la estructura de control de un AVR.
Este trabajo está organizado de la siguiente forma: en la sección 2 se describe el controlador PID, su algoritmo y requisitos de desempeño para un sistema de lazo cerrado. En la sección 3 se describe el AVR junto a cada uno de los elementos de su estructura. La sección 4 describe el Algoritmo de optimización Seno-Coseno. La sección 5 presenta el algoritmo SCA para sintonizar el controlador PID. Finalmente, algunos resultados de simulación son presentados.
2 Controlador PID
Dado el error e(t) = r(t) -y(t) y la salida u(t). El controlador PID ideal no interactivo o dependiente (ANSI/ISA) (6) es dado por:
Aplicando la transformada de Laplace a la ecuación (1) el controlador PID es reescrito como:
Observando la ecuación (3) se verifica que el controlador PID aumenta dos ceros y un polo a la función de transferencia de lazo abierto que representa la planta.
Para sintonizar las ganancias del controlador PID, se pueden aplicar diferentes métodos, el más conocido es el desarrollado por Ziegler-Nichols en el cual se debe obtener la ganancia crítica y el periodo crítico correspondiente, para este propósito se hace uso de las reglas presentadas en la Tabla 1:
Tabla 1 Sintonización de PID por Ziegler-Nichols
| Tipo | KP | Ti | Td |
|---|---|---|---|
| Proporcional | 0.5Kc | ||
| Proporcional - Integral | 0.45Kc | Tc/1.2 | |
| Proporcional- Integral - Derivativo | 0.75Kc | Tc/1.6 | Tc/10 |
El desempeño obtenido haciendo el ajuste de ganancias a través del método de Ziegler-Nichols puede ser mejorado haciendo uso de índices de desempeño como el IAE (Integral Absolute Error), el cual se trata de la integral del valor absoluto del error de la variable de control en cuestión. La ecuación (4) presenta este índice.
Los requisitos considerados para el ajuste de controladores tipo PID son presentados en la Tabla 2, los cuales fueron tomados de Ogata (3).
3 Regulador automático de tensión (AVR)
En los sistemas de potencia, el voltaje necesita mantenerse dentro de límites definidos y constantes, de lo contrario, el sistema sufre problemas de estabilidad y las cargas se alimentan con voltajes más bajos, por lo que se debe evitar la caída de voltaje en ellos. El AVR está diseñado para controlar y mantener el voltaje contaste en terminales del generador mediante la inyección de una corriente de campo.
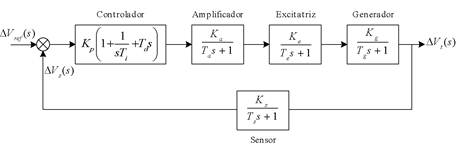
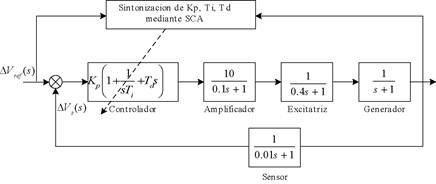
Un AVR en su forma genérica está compuesto por un amplificador, una excitatriz, un generador y un sensor, cada uno con sus funciones de transferencia específicas. Todos los componentes mencionados son ilustrados en la Figura 1, donde se muestra también el controlador PID.
En los trabajos de Hekimoglu (7) y Padiachy et al (10), son especificados los valores de cada uno de los parámetros del modelo AVR. Estos valores son presentados en la Tabla 3.
Tabla 3 Parámetros y valores del Sistema AVR
| Componente | Límites para Ganancia y Contantes de tiempo | Valores empleados |
|---|---|---|
| Amplificador | 10 ≤ Kɑ ≤ 40, 0.02 ≤Tɑ ≤ 0.1 | Kɑ = 10, Tɑ = 0.1 |
| Excitatriz | 1 ≤ K e ≤ 10, 0.4 ≤ Te ≤ 1 | Ke= 1 ,Te= 0.4 |
| Generador | 0.7 ≤ Kg≤ 1, 1 ≤ Tg ≤2 | Kg= 1 ,Tg= 1 |
| Sensor | 1 ≤ Ks ≤ 2, 0.001 ≤ Ts ≤ 0.06 | Ks= 1,Ts = 0.01 |
4 Optimización basada en el algoritmo seno coseno (SCA)
El SCA es desarrollado en el año 2016 por Mirjalili (5), en donde se expone este algoritmo para resolver problemas de optimización utilizando una técnica basada en la población, la cual busca estocásticamente los óptimos de los problemas en un conjunto de soluciones aleatorias, el óptimo es evaluado en ciertas iteraciones por una función objetivo para aumentar la probabilidad de encontrar el punto óptimo global. En otras palabras, la formulación matemática del SCA está basada en las funciones seno y coseno para explorar y explotar el espacio entre dos soluciones en el espacio de búsqueda y encontrar las mejores soluciones posibles (oscila dentro o fuera de la mejor solución.) (5).
Pese a que el algoritmo de senos y cosenos fue propuesto y expuesto hace pocos años, en la literatura se pueden encontrar diversas aplicaciones para el SCA en distintas áreas de aplicación.
Las fases de exploración y explotación son incluidas en las siguientes ecuaciones
Donde
Un algoritmo debería poder equilibrar la exploración y la explotación para encontrar la región más prometedora del espacio de búsqueda y, finalmente, converger al óptimo global. Para equilibrar la exploración y la explotación, el rango de seno y coseno en las ecuaciones (5) se cambia adaptativamente usando la siguiente relación:
Donde t es la iteración actual, T es el número total de iteraciones y ɑ es una constante de valor igual a 2, con estos valores se puede verificar que su valor decrece linealmente desde y hasta 0.
5 Aplicación de optimización al PID del AVR
En general, la metodología de diseño del controlador PID que utiliza el error absoluto integrado (IAE), el error cuadrático integral (ISE) o el error cuadrático ponderado en el tiempo (ITSE), a menudo es empleada en el diseño del sistema de control porque se puede evaluar analíticamente en el dominio de la frecuencia y en el dominio del tiempo. Los tres criterios de rendimiento integral en el dominio del tiempo y la frecuencia tienen sus propias ventajas y desventajas. Por ejemplo, una desventaja de los criterios IAE e ISE es que su minimización puede dar como resultado una respuesta con un sobrepaso relativamente pequeño, pero con un tiempo de establecimiento largo porque el criterio de desempeño ISE pondera todos los errores por igual independientemente del tiempo. Aunque el criterio de desempeño ITSE puede superar la desventaja del criterio ISE, los procesos de derivación de la fórmula analítica son complejos y requieren mayor tiempo.
De esta forma, la función a ser optimizada es dada por la ecuación (7):
Finalmente, la Figura 2 ilustra la estructura de simulación implementada en este trabajo.
6 Resultados de simulación
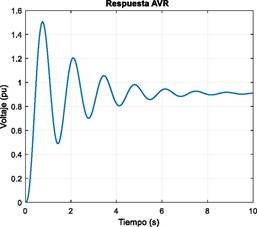
La primera simulación realizada corresponde al sistema de lazo cerrado es decir el AVR sin controlador PID. La Figura 3 ilustra la respuesta a escalón en donde se verifica el comportamiento oscilatorio del mismo debido justamente a la falta de control.
El comportamiento oscilatorio sub-amortiguado (factor de amortiguamiento menor a 1), presenta un error en estado estacionario de aproximadamente 10% con un tiempo de estabilización o asentamiento mayor a 10 segundos y con un sobre paso del 65%. En este sentido, el desempeño de este AVR está lejos de presentar un comportamiento adecuado.
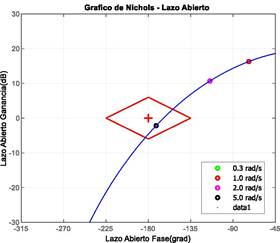
Adicionalmente, la Figura 4 ilustra la carta de Nichols (8, 9) que aporta información en el dominio de la frecuencia, la misma muestra un margen de ganancia y de fase reducido que compromete la robustez del sistema. Los valores que se pueden extraer de la Figura 4 corresponden a un margen de ganancia de 4.62 dB y margen de fase de 16.10 grados, valores mucho menores a los requisitos.
La Tabla 4 se resume los parámetros en forma de desempeño del sistema AVR en lazo cerrado sin la presencia del controlador PID.
Tabla 4 Parámetros de desempeño del sistema AVR sin PID
| Parámetros | Valores |
|---|---|
| Máximo Sobrepaso | M p = 65.20% |
| Tiempo de Elevación | t r = 0.25s |
| Tiempo de Establecimiento | t s = 7s |
| Tiempo pico | t p = 0.75s |
| Margen de Ganancia | Mg = 4.62dB |
| Margen de Fase | Mf = 16.10º |
En seguida, empleando el método de Ziegler-Nichols se obtienen los siguientes valores para las ganancias del controlador PID (ver Tabla 1): Kp = 1, Ti = 1.3409, Td =0.41557. El procedimiento es detallado en Ogata (3).
Finalmente, para la sintonía por optimización a través del algoritmo Seno- Coseno, se parte de las siguientes condiciones iniciales:
Tabla 5 Parámetros para la optimización vía SCA
| Parámetros | Valores |
|---|---|
| Población | i = 40 |
| Numero de Iteraciones | t = 100 |
| Rango Ganancia Proporcional | K p =[0.3,1] |
| Rango Tiempo Integral | T i =[0.3,1] |
| Rango Tiempo Derivativo | T d = [0.3,1] |
| Función de minimización |
|
Ahora, empleando el SCA se obtiene el valor mínimo de la función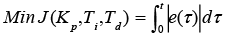 
. La característica de convergencia y las iteraciones son ilustradas en la Figura 5.
Realizada la sintonía de las ganancias del PID para los dos métodos presentados, es realizada la respectiva comparación cuantitativa cualitativa. La diferencia de valores para las ganancias de los métodos es presentada en la Tabla 5.
Tabla 6 Ganancias de controlador PID
| Ganancias | Ziegler-Nichols | SCA |
|---|---|---|
| Ganancia Proporcional | Kp = 1 | Kp = 1 |
| Tiempo Integral | Ti = 1.3409s | Ti = 1.2863s |
| Tiempo Derivativo | Td = 0.4155s | Td = 0.4230s |
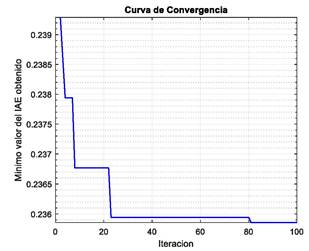
La Figura 6 ilustra la respuesta a escalón del sistema AVR sin controlador PID y con los dos PID sintonizados. En esta respuesta se verifica que el AVR con PID cuyas ganancias fueron obtenidas empleando el algoritmo SCA presenta mejores valores de índices de desempeño comparado con su par obtenido mediante Ziegler- Nichols, tal como lo muestra la Tabla 7.
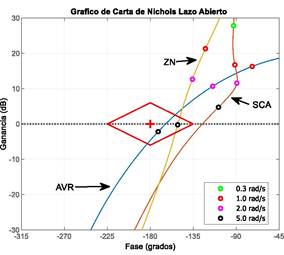
La Figura 7 ilustra la carta de Nichols con las tres respuestas, AVR sin controlador, AVR con PID sintonizado empleando el método de Ziegler-Nichols y finalmente, el AVR con PID sintonizado a través del algoritmo de optimización SCA.
Los valores de desempeño para las sintonías vía Ziegler-Nichols y SCA, son presentados en la Tabla 6.
Tabla 7 Comparación de Resultados de Simulación Ziegler-Nichols vs SCA
| Parámetros | Ziegler Nichols | SCA |
|---|---|---|
| Máximo Sobrepaso | Mp = 46.49% | Mp = 10.1% |
| Tiempo de Elevación | tr = 0.25s | tr = 0.24s |
| Tiempo de Establecimiento | ts = 3.1s | ts = 1.35s |
| Tiempo pico | tp = 0.6s | tp = 0.31s |
| Margen de Ganancia | Mg = 25.5dB | Mg = 23dB |
| Margen de Fase | Mf = 29.98º | Mf = 50.2º |
En la Tabla 7 se verifican los valores del margen de ganancia y de fase para los dos casos presentados. El algoritmo SCA es el que presenta mejor desempeño que Ziegler-Nichols, debido a que el margen de fase es 23 dB mayor a los 6 dB exigidos (3) y un margen de fase de 50 grados valor que se encuentra entre los 45 y 60 grados del requisito.
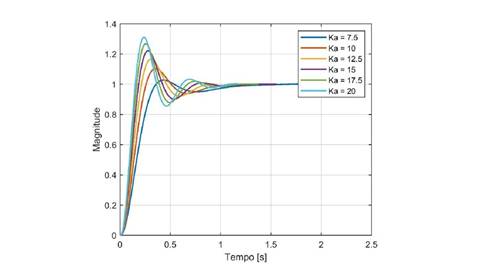
La robustez para el PID basado en SCA es estudiada considerando diferentes valores de la ganancia Ka La Figura 8 lustra la respuesta a escalón obtenida para los diferentes casos. Se verifica el aumento del sobre impulso a mediada que el valor de Ka aumenta.
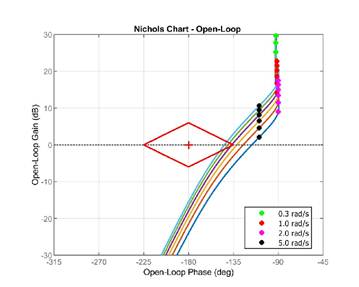
La Carta de Nichols para los casos estudiados es lustrada en la Figura 9. Complementando la respuesta a escalón se observa que, para el aumento de Ka, los márgenes de ganancia y fase disminuyen.
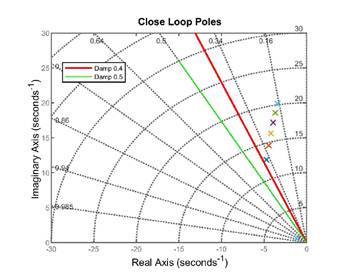
Finalmente, la Figura 10 ilustra los polos de lazo cerrado donde se verifica que la amortiguación es mayor a 0.4 o está próximo de ese valor cumpliendo los requisitos exigidos. Se debe observar también que uno de los 5 polos se encuentra en -102 por lo que no aparece en el diagrama presentado.
7 Conclusiones
El desarrollo de este trabajo supuso inicialmente el estudio de técnicas de optimización y el objetivo que las mismas persiguen. En secuencia se hizo uso del Algoritmo Seno-Coseno SCA para sintonizar las ganancias del controlador PID, en su forma no interactiva o dependiente (ANSI/ISA). El proyecto integra el algoritmo SCA con la función de optimización de la integral absoluta del error IAE.
Los resultados de simulación obtenidos muestran que el controlador propuesto puede realizar una búsqueda eficiente para determinar las ganancias óptimas del controlador PID. Se realizó la comparación de desempeño en el tiempo y en frecuencia para los dos métodos presentados. Es evidente que el análisis basado en la carta de Nichols si bien no es novedosa, permite extraer valiosa información de robustez en una gráfica. Las simulaciones realizadas permitieron verificar que el algoritmo SCA es superior al método Ziegler-Nichols, por lo que es posible utilizarlo para sintonizar los AVR’s industriales presentes en el mercado eléctrico.
