Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Acta Nova
versión On-line ISSN 1683-0789
RevActaNova. v.9 n.5-6 Cochabamba nov. 2020
Artículo Científico
Special Sheffer-operators on a p-valued logic
Operadores de Sheffer especiales en una lógica p-valuada
Oscar R. Pino Ortiz
Universidad Católica Boliviana, Cochabamba, Bolivia
Los Nogales 2030 Cbba,
Recibido: 12 de marzo 2020
Aceptado: 2 de septiembre 2020
Abstract: We studied the Sheffer-operators that can be written under the form 1 + α(r,s) where α is an associative, commutative and idempotent operator on Zp[x, y], with p prime. We conjecture that such operators are always Sheffer operators. We show the conjecture is true for p = 2 and p = 3.
Key words: Logic, Multivalued, Sheffer.
Resumen: Se estudia los operadores de Sheffer que pueden escribirse bajo la forma 1 +α(r,s), donde α es una operación asociativa, conmutativa e idempotente sobre Zp[x, y], con p primo. Conjeturamos que tales operadores son siempre operadores de Sheffer y mostramos que la conjetura es cierta para p = 2 y p = 3.
Palabras Clave: Lógica, Multivaluada, Sheffer.
1 Introduction
In a previous article [1] we have shown that every operator in a p-valued logic can be written as a polynomial in Zp [x, y]. We have also remarked that three of the most known multivalued Sheffer-operators can be written as 1 +α(x, y), where α is associative, commutative and idempotent on its variables. This is the case of Post-operator inc(min(x, y)), the Webb-operator inc(max(x, y)) and the Webb stroke function |, whose polynomial form is δ1.
For instance, if p = 3, the three mentioned operators are:
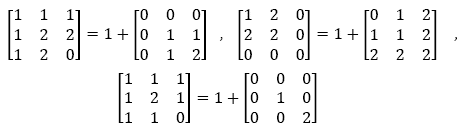
whose polynomial expressions2 are:

Of course, these three operators are not the only ones that have the properties indicated above. How many there are? Which are they? Are all the operators with these properties Sheffer-operators?
2 A theorem on special Sheffer-operators
To answer these questions, we introduce an action of the Sp group on the set Zp[x, y] defined by
![]()
Where θ ![]() Sp. It is clear that θ * γ is in Zp[x, y] if γ is in Zp[x, y].3
Sp. It is clear that θ * γ is in Zp[x, y] if γ is in Zp[x, y].3
Let's take Sp =< ρ; τ >, where ρ is the first p-cycle and τ is the transposition between 0 and 1. For instance, if p = 3 , we have ρ(x) = 1 + x and τ(x) = 1 + 2x.
Theorem 1 Let be θ ![]() Sp and γ
Sp and γ ![]() Zp[x, y].
Zp[x, y].
θ * γ is a Sheffer operator if γ it is.
Proof
For an operator γ(x, y) ![]() Zp[x, y], define Im(γ) in a recursive way:
Zp[x, y], define Im(γ) in a recursive way:
1) x ![]() Im(γ)
Im(γ)
2) y ![]() Im(γ)
Im(γ)
3) r,s ![]() Im(γ)
Im(γ) ![]() γ(r,s)
γ(r,s) ![]() Im(γ)
Im(γ)
Then γ is a Sheffer-operator if and only if Im(γ) = Zp[x, y].
Now, if γ is a Sheffer-operator4, it is easy to see that x, y ![]() Im(θ * γ). Indeed θ * x = x and θ * y = y.
Im(θ * γ). Indeed θ * x = x and θ * y = y.
Now let be r and s in Im(γ). Then γ(r, s) ![]() Im(γ). Since γ is a Sheffer operator we have that θ-1(r) and θ-1(s) are in Im(y). So we can use the identity:
Im(γ). Since γ is a Sheffer operator we have that θ-1(r) and θ-1(s) are in Im(y). So we can use the identity:
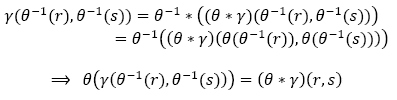
That is if γ(r, s) ![]() Im(γ) then γ(θ-1(r),θ-1(s))
Im(γ) then γ(θ-1(r),θ-1(s)) ![]() Im(γ) and then:
Im(γ) and then:
![]()
Like θ: Zp[x, y] ![]() Zp [x, y] is a one to one map, whose inverse is θ-1, we have
Zp [x, y] is a one to one map, whose inverse is θ-1, we have
![]()
Theorem 2
If α ![]() Zp[x, y] is associative, so θ *α it is.
Zp[x, y] is associative, so θ *α it is.
If α ![]() Zp[x, y] is commutative, so θ * α it is.
Zp[x, y] is commutative, so θ * α it is.
If α ![]() Zp[x, y] is idempotent, so θ * α it is.
Zp[x, y] is idempotent, so θ * α it is.
Proof
1. Suppose that α ![]() Zp[x, y] is associative. It means α(r, α(s,t)) = α(α(r,s), t) for all r, s, t
Zp[x, y] is associative. It means α(r, α(s,t)) = α(α(r,s), t) for all r, s, t ![]() Zp[x,y].
Zp[x,y].
Then
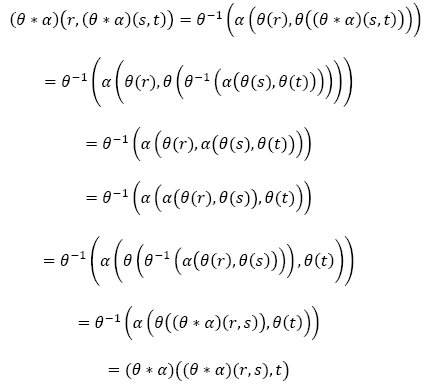
2. Suppose that α ![]() Zp[x,y] is commutative. It means α(r,s) = α(s,r) for all r,s
Zp[x,y] is commutative. It means α(r,s) = α(s,r) for all r,s ![]() Zp[x,y].
Zp[x,y].
![]()
3. Suppose that α ![]() Zp[x,y] is idempotent. It means α(r,r) = r for all r
Zp[x,y] is idempotent. It means α(r,r) = r for all r ![]() Zp[x, y].
Zp[x, y].
![]()
Corollary
Let be
Ap = { α ![]() Zp[x,y] | α is asociative, comutative and idempotent}.
Zp[x,y] | α is asociative, comutative and idempotent}.
If α ![]() Ap then θ * α
Ap then θ * α ![]() Ap.
Ap.
Cases p = 3 and p = 5
For p = 3 we have nine polynomials of the form 1 + α(x, y) with α ![]() A3. α must be one of:
A3. α must be one of:

We see that α1 = α|, α2 = ![]() and α7 = αv. All nine 1 + αi(x,y) are Sheffer operators. We have two orbits:
and α7 = αv. All nine 1 + αi(x,y) are Sheffer operators. We have two orbits:
![]()
Using a computer, for p = 5 we have found 1065 Sheffer operators of this special form. We conjecture that if an operator has this special form then it is a Sheffer operator. This assumption is true for little values of p prime. For instance, for p = 2 we have only two Sheffer operators 1 + xy and 1 + x + y + xy, the Sheffer stroke and the Pierce arrow and, in this case, it is very easy to show that the conjecture is true. For p = 3 we are in a similar situation, because under the conditions imposed to α ![]() A3 we found that 1 +α(x, y) is one of the nine Sheffer operators listed above. Indeed...
A3 we found that 1 +α(x, y) is one of the nine Sheffer operators listed above. Indeed...
Theorem 3
If γ(x,y) = 1 + α(x,y) is an operator of a 3-valued logic with α ![]() A3, γ is a Sheffer operator.
A3, γ is a Sheffer operator.
Proof
Since α is commutative and idempotent, the matrix form5 of α is  with a, b, c
with a, b, c ![]() Zp. Of course, we have α(0,1) = a, α(0,2) = b and α(1,2) = c.
Zp. Of course, we have α(0,1) = a, α(0,2) = b and α(1,2) = c.
There are 27 cases.
If a = 2 then b = 2 and c = 2, because
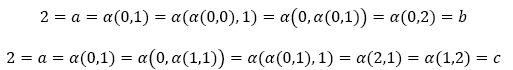
By the same way we can show that:
if b = 1 then a = 1 and c = 1
if c = 0 then a = 0 and b = 0
So we have the following three operators in A3
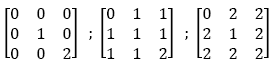
On the other hand we can exclude all the operators failing the rules showed above. There are 1·3·3 + 2·1·3 + 2·2·1 - 3 = 16 of them. They all are not associative.
There are eight operators left to study. For them we have a ![]() {0; 1}, b
{0; 1}, b ![]() {O;2}, c
{O;2}, c ![]() {1;2}.
{1;2}.
We see there are two cases that are clearly not associative: a = 0, b = 2, c = 1 and a = 1, b = 0, c = 2 because
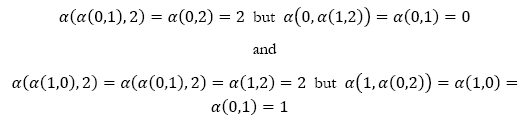
The six operators remaining are:

They are all six associative.
We recognize the two orbits formed by the action of S3 on A3. In the first orbit there is the well-known operator 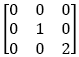 corresponding to α|(x,y). Since 1 + α|(x, y) is the Webb stroke and it is a Sheffer operator, all the operators in its orbit define also Sheffer operators.
corresponding to α|(x,y). Since 1 + α|(x, y) is the Webb stroke and it is a Sheffer operator, all the operators in its orbit define also Sheffer operators.
In the second orbit we have another operator we know quite well: 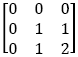
It corresponds to ![]() (x, y). Like 1 +
(x, y). Like 1 + ![]() (x, y) is the Post-operator and it is a Sheffer operator we have again that all the operators in its orbit define Sheffer operators.
(x, y) is the Post-operator and it is a Sheffer operator we have again that all the operators in its orbit define Sheffer operators.
Notes
1 δ is a Sheffer-operator. Donald L. Webb showed it in 1935 [3]. We rewrote the proof under an algebraic point of view [2].
2 The way we build the polynomial expression of a logic operator is explained in detail in [2].
3 You can easily see that * thus defined is an action à droite of a group on a set.
4 Remember that a logic operator γ is called a Sheffer operator if and only if all the logic operators may be written using only γ.
5 See [2].
Bibliography
[1] Pino O., Morales Z. (2015) Un operador de Sheffer en la Lógica IGR3. Acta Nova, Vol 7, Nº1. Cochabamba, Bolivia.
[2] Pino O. (2018) Un operador de Sheffer en la Lógica IGRp. Acta Nova, Vol 8, Nº4. Cochabamba, Bolivia.
[3] Webb D. L. (1935). Generation of any n-valued logic by one binary operation. Proceedings National Academy of Sciences. U.S.A. May 1935.
[4] Stojmenovic I., (1988). On Sheffer symmetric functions in three valued logic. Discrete Applied Mathematics 22, North-Holland. [ Links ]
[5] Foxley E., (1962) The determination of all Sheffer functions in 3-valued logic, using a logical computer. Notre Dame Journal of Formal Logic, Volume III, Number 1. Nottingham, England.