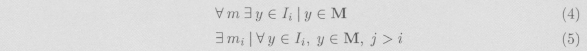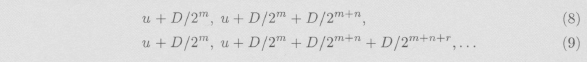Historia de las Ciencias

 

El Teorema del Valor Intermedio y la Completitud de los Reales
Segunda Parte

 

 

Mauricio Navia Lora

Centro de Investigación Matemática
Universidad Católica Boliviana San Pablo
Cochabamba - Bolivia
e-mail: navia@ucbcba.edu.bo

 

 

---

Según hemos visto en la primera entrega de este artículo [2], Cauchy y Bolzano en el siglo diecinueve sentaron las bases rigurosas del cálculo. Es cierto que la madurez plena del análisis matemático no se alcanzó hasta la llegada de Weierstrass y sus funciones especiales, por un lado, y de Dedekind-Cantor y la construcción axiomática de los números reales por otro.

Sin embargo, el trabajo de Cauchy y Bolzano fue crucial para tender un puente del cálculo "naïve" del siglo XVIII al análisis moderno. De estas dos figuras de la matemática, el nombre de Cauchy es mucho más conocido y a él están asociados una gran cantidad de teoremas estudiados en los primeros semestres de la universidad (ej: teorema del valor medio de Cauchy, ecuación de Cauchy-Euler, condiciones de Cauchy-Riemann, teorema de la integral de Cauchy-Goursat, etc.). En efecto el aporte de Cauchy fue sumamente importante sobre todo en áreas que tienen que ver con las aplicaciones del cálculo, es decir, las ecuaciones diferenciales, el análisis complejo, etc.

En cambio el nombre de Bolzano resulta bastante más modesto y su aporte parece escueto. No obstante en cuanto a profundidad lo que hizo Bolzano fue de mucha calidad y significación; y aunque su influencia no fue inmediata, él anticipó varias ideas cruciales en la construcción del análisis matemático de autores medio siglo posteriores a él.

La contribución de Bolzano está recibiendo una nueva evaluación relativa a su importancia. Esta va más allá de los límites de la historia de las matemáticas, es decir de una curiosidad académica, y de un posible aporte que este conocimiento daría a la educación matemática universitaria, llegando a ser de interés para las ciencias de la computación. A este respecto, el investigador británico a cuyo cargo está el proyecto de traducir y comentar la obra de Bolzano (y cuya versión utilizamos para el presente artículo), Steve Russ, afirma lo siguiente¹:

"Bernard Bolzano (active in the first half of the 19th century) made outstanding conceptual and technical contributions to logic and mathematics, foreshadowing Tarski's semantic notions of truth and consequence, Cauchy's concepts of convergence and continuity, Weierstrass' insights into highly pathological (fractal) functions, and Cantor's establishment of a theory of infinite sets. A major series of translations (of 9 German publications or manuscripts) is forthcoming in The Mathematical Works of Bernard Bolzano to be published by Oxford University Press.

Bolzano's insights were founded on the very clear separation of objective meanings from psychological events, linguistic expressions and real-world objects (if any). This was at a time prior to the domination of mathematics and logic by methods of abstraction and formalism. Modern computing was born, and developed, under the influence (perhaps undue influence) of a mathematical and formal perspective. Current research on Bolzano is part of a larger enquiry into the principies underlying the accommodation of formal and informal elements in both 19th century mathematics and modern computing" [3]

Con estas afirmaciones, Russ le confiere una novedosa relevancia al estudio de Bolzano, y plantea un desafío a quienes deseen conocer algo sobre el desarrollo de la historia de la matemática, la informática y la lingüística.

En cuanto a lo que, por el momento, nos atañe, en primer lugar, está la insistencia de Bolzano en que las demostraciones matemáticas deben prescindir de la intuición geométrica. Su artículo sobre el teorema del valor intermedio [1], que buscaba dar una prueba "puramente analítica" de que dos funciones continuas, creciente y decreciente, deben intersectarse en un punto, es un ejemplo clásico de dicha insistencia. Como dijimos en la anterior entrega, Bolzano no llegó a demostrar el teorema clave necesario para sustentar el del valor intermedio; sin embargo, su esfuerzo fallido es notable y arroja mucha luz sobre las dificultades filosóficas, nada triviales, que plantea el análisis, además de las implicaciones que su resolución han tenido en el desarrollo del resto de las matemáticas. Por ejemplo lo que hoy se da por sentado: la necesidad de demostrar "lo obvio", lo trivial. Retomemos la formulación original de Bolzano:

"Sea M la propiedad no poseída por todos (no válida para todos) los valores de la variable x pero que sí lo es para todos los valores menores a un cierto u. Existe un U que es el mayor de aquellos para quienes puede aseverarse que todos los x menores poseen la propiedad M"².

Como indicamos anteriormente es mucho más económico decir

"Para un conjunto M, no vacío, el conjunto M* = {u | ( -∞, u) M} posee un elemento máximo, U "

También en la primera entrega se mostró que esta proposición es equivalente al axioma de completitud de Dedekind. Ahora veamos críticamente el intento de demostración del teorema anterior, según Bolzano:

Sea u + D un número (el cual existe por hipótesis) que no posee la propiedad M. Considérese la secuencia de intervalos I_m = {(u, u + D/2^m)}.

Ahora bien, para todo m existe al menos un número y en el intervalo I_m, que carece de la propiedad M, o bien, existe un m = m_¡ mínimo tal que todos los números en los intervalos, {(u,u+ D/2^m)}, j > i, tienen la propiedad M. En el primer caso el U buscado es simplemente u. Si se da el segundo caso, constrúyase el intervalo

Del mismo modo, para todo n existe al menos un número en el intervalo sin la propiedad M, o bien existe un n menor tal que todos los números de los intervalos

tienen la propiedad M. En el primer caso

De modo más compacto:

Sea u + D , de modo tal que, u + D M

Sea I_i = {(u,u + D/2^m)} una secuencia de intervalos. Hay dos posibilidades:

Si (4) U = u, y el teorema queda probado.

Si (5):

o bien

Si (6) U = u + D/2^m

Y si (7) continuar el proceso como se ha descrito para crear la secuencia:

U puede definirse como el límite de la secuencia anterior. Bolzano intentó demostrar la convergencia de la secuencia anterior. Como se sabe, una secuencia de Cauchy en es convergente, es decir, cuando dos términos de la secuencia pueden ser arbitrariamente aproximados, ésta converge, según el Criterio de Cauchy, a algún límite:

Sin embargo, esto no nos garantiza la existencia del límite. Mientras no exista una construcción adecuada de los números reales, tal cosa no es posible. A Bolzano se le escapó esta sutileza. Varias décadas después, Richard Dedekind llegó a completar el hueco que faltaba en los fundamentos del análisis real. Sin embargo, el mérito de Bolzano sigue en pie al haber abierto este cuestionamiento. El propio Dedekind así supo reconocerlo.

 

Notas

¹ "Bernard Bolzano realizó notables contribuciones técnicas y conceptuales a la lógica y las matemáticas, preludiando las nociones semánticas de verdad y consecuencia de Tarski, los conceptos de convergencia y continuidad de Cauchy, las intuiciones de Weierstrass sobre funciones altamente patológicas (fractales) y la teoría de conjuntos finitos de Cantor...

Las geniales intuiciones de Bolzano se basaban en una clara separación de significados objetivos de eventos psicológicos, expresiones lingüísticas y objetos del mundo real (si alguno existe). Esto ocurrió en un período anterior al predominio de los métodos abstractos y formales en lógica y matemáticas. .. "

² El subrayado es nuestro.

 

Referencias

[1] B. Bolzano. Rein Analytischer Beweis des Lehrsatzes, dass Zwischen je zwey Werthen, die ein Entgegengesetztesn Resultat Gewahern, Wenigstens eine Reelle Wurzel der Gleichung Liege. prague: Gottlieb Haase, 1817. p. 60.        [ Links ]

[2] M. Navia. El teorema del valor intermedio y la completitud de los reales. Acta Nova, 1(2): 123-133, 2001.        [ Links ]

[3] The mathematical works of bolzano. www.dcs.warwick.ac.uk/hoc/mwb.html. University of Warwick.