Artículo Científico

 

Sobre una Trasgresión Numérica

 

 

Oscar R. Pino Ortiz

Centro de Investigación Matemática - C.I.M.A.
Universidad Católica Boliviana San Pablo
Cochabamba, Bolivia
e-mail: pino@ucbcba.edu.bo

 

 

---

Resumen

Es bien conocido que si una sucesión real monótona creciente es acotada, entonces el límite de dicha sucesión existe y es menor o igual a la cota. Este trabajo muestra que tal afirmación no es verdadera si se toma como cota No. Lo que aparentemente significaría una seria dificultad para la extensión de las técnicas del análisis clásico al estudio de las sucesiones transfinitas.

---

 

 

1    Conceptos Preliminares

Sea |C| la categoría de los conjuntos con las aplicaciones como morfismos. Podemos definir sobre los objetos |C| de esta categoría una relación de equivalencia por medio de:

Un número cardinal es entonces una clase de equivalencia de |C| (que no es un conjunto) para la relación .

Recordemos algunos de los números cardinales conocidos: 0,1,2,3,..., ₀, ₁, ₂, ... Los primeros 0,1,2,3,... son también llamados cardinales finitos y los segundos ₀, ₁, ₂, ..., cardinales infinitos [1, 2].

Recordemos, igualmente, que decimos que un conjunto a es infinito si existe una aplicación de a en a, inyectiva no sobreyectiva [3].

Aunque la intuición muestra como evidente que podemos definir una relación de orden total y natural sobre los números cardinales, no es fácil probar, por ejemplo, que si α y β son cardinales, entonces

Esta última afirmación es conocida bajo el nombre de Teorema de Cantor-Bernstein [3].

Consideremos la subcategoría ε C tal que |ε| = |C| y tal que los morfismos de ε sean los monomorfismos de C. No presenta dificultad mostrar que es posible definir, de manera natural, un funtor covariante k : ε → Ñ , donde Ñ es la categoría de los números cardinales cuyos objetos son la clase de los símbolos 0,1,2,3,..., ₀, ₁, ₂.....provistos de los siguientes morfismos:

La composición de morfismos es, evidentemente, 1_βγ o 1_αβ =1_αγ

 

2    La trasgresión

Un resultado conocido en análisis es el que afirma que si u : → ⁺ es un sucesión positiva tal que u_n < a entonces

El corazón del presente artículo es mostrar que este teorema es falso si consideramos una sucesión u : → Ñ. En efecto vamos a probar que es posible construir una sucesión u en Ñ tal que u_n < ₀ y sin embargo .

Sea A_n , un conjunto de cardinalidad n, digamos A_n = {1; 2; 3;...; n}. La cardinalidad de P(A_n) es 2ⁿ. La sucesión que nos interesa es definida como la composición de:

Es decir, u : → Ñ es tal que u_n = u(n) = k(P(A_n)) = 2ⁿ. Es claro que 2ⁿ < ₀ n Є . Sin embargo,

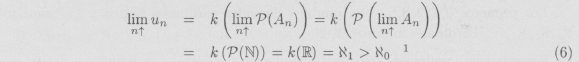
El único punto cuyo significado puede ser eventualmente algo confuso es el de .

Basta observar que A₁ A₂ A₃ ... A_n , que por lo tanto

y que

Peor aún, podemos mostrar que el límite de una sucesión constante no os lo que uno espera, es decir, la constante. En efecto, consideremos la sucesión ν : → Ñ tal que v_n = v(n) = kⁿ). Esta sucesión es constante porque x y entonces ⁿ n . Podemos escribir v_n = k(ⁿ) = ₀, n . Pero si tomamos el límite cuando n crece indefinidamente...

Sorprendente ¿no es verdad?. Pero no tanto si consideramos una "evaluación" discontinua sobre, por ejemplo, el intervalo [0; 1]:

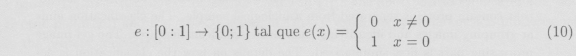
Ahora, si definimos la sucesión v : → [0;1] por v_n = e (1/n), tendremos la sucesión constante v_n = 0 cuyo límite, cuando n crece indefinidamente, no es 0, sino 1. En efecto:

A todas luces, en este caso, la "sorpresa" viene del intercambio .

Estamos tentados a deducir que el funtor k se comporta como una "evaluación discontinua" entre la finitud y la infinitud. Así se explicaría la trasgresión numérica que nos ocupó en estas notas.

 

Notas

¹No está demás aclarar, para los lectores no matemáticos, que la igualdad se demuestra observando que ambos conjuntos poseen los mismos elementos. Por ejemplo, está claro que y por lo tanto que . Para ver que también pertenece a , basta observar que . Así, todo subconjunto M de pertenecerá a , ya que . Concluimos que . La otra inclusión no presenta dificultad ya que es bien sabido que . Por lo tanto ambos conjuntos tienen la misma cardinalidad ₁.

 

Referencias

[1] G. Cantor. Contributions to the foundings of the theory of Transfinite Numbers. Dover Publications, New York, 1955.        [ Links ]

[2] L. Rodríguez y O. Pino. Irracionalidad y Trascendencia. Inédito, 1994.

[3] S. Vasilach. Ensernbles, Structures, Catégories, Faisceaux. Masson, Paris, 1977.        [ Links ]