Artículo Científico

 

Niveles Energéticos Electrónicos en Nanopartículas

 

 

Rolando Saniz Balderrama

Departamento de Ciencias Exactas
Universidad Católica Boliviana San Pablo
Cochabamba, Bolivia
e-mail: saniz@ucbcba.edu.bo

 

 

---

Resumen

En este trabajo se estudian los niveles energéticos electrónicos en un punto cuántico representado por un pozo de potencial esférico de paredes infinitamente altas. Se toma en cuenta la interacción electrón-electrón dentro de una aproximación de Hubbard y se calculan las energías perturbativamente al primer orden. Los niveles energéticos encontrados son acordes a las reglas de Hund.

Palabras Clave: Quantum dot, many-body effects.

---

 

 

1    Introducción

La física de los sistemas de baja dimensión en el campo de la materia condensada constituye un área de gran actividad científica desde el descubrimiento del efecto Hall cuántico en un sistema electrónico bidimensional, descubrimiento realizado por Klaus von Klitzing a principios de la década de los 80. Un sistema de baja dimensión es aquél en el que los constituyentes dinámicos, e.g., electrones, fotones o fonones, tienen restricciones de desplazamiento en una o más dimensiones [1]. Este campo se ha desarrollado muy rápidamente, dando lugar a lo que ahora se llama "nanociencia" y, desde el punto de vista de las aplicaciones, "nanotecnología". [2, 3].

Uno de los sistemas que ha recibido más atención en los últimos años es el "quantum dot" o "punto cuántico". Este es esencialmente un pozo de potencial de dimensiones muy reducidas, capaz de confinar a los electrones en el material, generalmente un semiconductor, a regiones de diámetro del orden de un nanómetro. Además de su interés intrínseco en física por la riqueza de la fenomenología a la que dan lugar [4], los puntos cuánticos han merecido mucho estudio por sus potenciales aplicaciones, por ejemplo, en computación cuántica [5, 6].

La fenomenología de un sistema electrónico depende de manera fundamental de su espectro energético, por lo que en este trabajo se estudia este espectro para un modelo simplificado de punto cuántico. Se estudia también la corrección al espectro introducida por la interacción Coulombiana entre electrones. Este es un trabajo previo al análisis más detallado de las observaciones experimentales, vía desintegración de positrones, efecto tunel u otros, y a la elaboración de un modelo más realista.

Este trabajo está organizado como sigue. La siguiente Sección trata de los estados independientes de un electrón en un modelo de punto cuántico. En la Sección 3 se estudia el cambio del espectro energético debido a la interacción de Coulomb. En la Sección 4 se presentan los resultados, junto con una breve discusión.

 

2    Estados propios de una partícula independiente

Uno de los primeros modelos para el estudio de sistemas de partículas cargadas confinadas a una región muy pequeña del espacio, fue el modelo de potencial esférico de profundidad infinita empleado en física nuclear para el estudio del núcleo atómico [7]. Por esta razón, tomamos prestado el modelo para el presente estudio.

Sea una partícula de masa m confinada en un potencial esférico de radio R de la forma

La ecuación de Schrödinger de la partícula es

Si se escribe la función de onda de la partícula en términos de armónicas esféricas como φ(r) = Y_lm(θ,Φ)f(r), se obtiene una ecuación para la función radial

Las soluciones de esta ecuación están dadas por las funciones esféricas de Bessel, de primera y segunda especie, j_l y y_l, respectivamente [8]. Sin embargo, la condición de finitud f(r) < M para r → 0, donde M es un entero positivo finito, elimina las últimas. Por otra parte, la condición f(r) = 0 en r = R determina las energías propias del sistema ε_nl. En efecto,

y ε_nl = h²k²_nl/2m, donde el índice n recorre los ceros de j_l. Cabe hacer notar que estos ceros son aislados y forman una sucesión estrictamente creciente, es decir, para l y R fijos, k_nl < k_{n+1 l}, n. [8]. Las funciones propias de H₀ se pueden escribir entonces

con la constante de normalización dada por A_nl = 2/R³j(k_nlR). Estas soluciones constituyen un conjunto ortonormado, i.e., _nlm|_n´l´m' = δ_nn'δ_ll'δ_mm'. Se deriva un conjunto ortonormado de funciones propias reales definiendo, para m > 0,

y

Asi se obtiene finalmente el conjunto de estados utilizados en el presente estudio, a saber

con n = 1,2,3,..., l = 0,1,2,... y m = -l,-l+1,...,l-1,l.

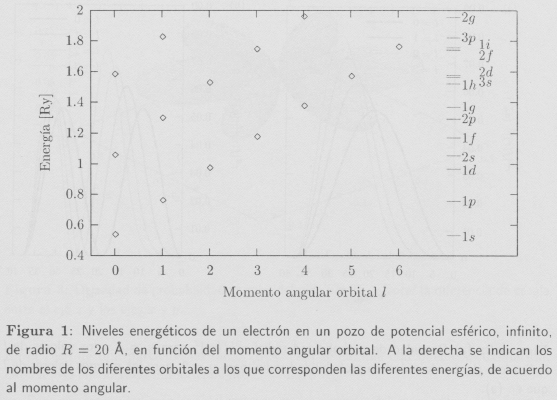
Para ilustrar estos resultados, mostramos en la Fig. 1 los catorce primeros niveles energéticos de un electrón en un pozo de potencial de radio R = 20 Å, en función del número cuántico asociado al momento angular orbital, l. Lamentablemente, no existe ninguna relación simple entre los ceros de las funciones de Bessel, por lo que, contrariamente a la impresión que puede dar el gráfico, no se puede determinar de manera general ε_{n+1 l} a partir de ε_nl, ni ε_{n l+1} a partir de ε_nl. En la figura también se indican los nombres que reciben los orbitales que corresponden a las diferentes energías de acuerdo a la nomenclatura de la física atómica. Como en ese caso, las energías presentan degenerescencia en cuanto al spin y al número cuántico magnético m. Sin embargo, a diferencia del caso atómico, los niveles energéticos en el presente caso no presentan degenerescencia en l para un mismo nivel n, lo que hace que el espectro de energía tenga mayor estructura y pueda dar lugar a una fenomenología más rica debido a la mayor diversidad de transiciones electrónicas posibles.

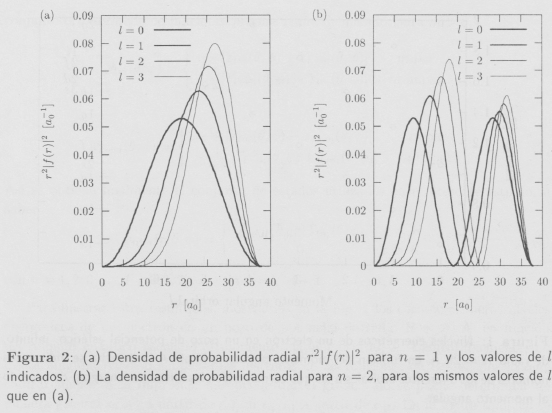
En la Fig. 2 se muestra el comportamiento radial de las funciones a través de la dependencia radial de la densidad de probabilidad, r²|f(r)|². El número de máximos está dado por el nivel energético n, independientemente del valor de l. Esto ilustra gráficamente las contribuciones a la energía cinética de la partícula de la energía cinética radial (derivada radial de la función de onda), que incrementa con n, y del momento angular, que incrementa con l. En la misma figura se puede apreciar, además, que la probabilidad de encontrar la partícula cerca al centro del potencial disminuye al incrementar el momento angular, como es de esperar. El comportamiento radial de la densidad de probabilidad debe ser complementado, desde luego, con el comportamiento angular de la misma. Puesto que la dependencia angular de las funciones de onda está dada por las armónicas esféricas, el comportamiento angular de la densidad de probabilidad es, obviamente, similar al de los orbitales atómicos.

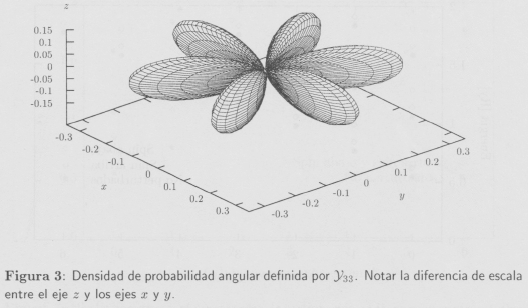
En la Fig. 3, por ejemplo, mostramos el comportamiento angular de la densidad de probabilidad dada por Y₃₃, que es un orbital ƒ. El gráfico muestra una ilustrarán paramétrica de |Y₃₃ (θ,Φ)|². La escala del eje z fue modificada para visualizar mejor la forma del orbital. Debido a la similitud de las funciones de onda electrónicas en un punto cuántico y las funciones de onda electrónicas atómicas, los puntos cuánticos son a veces llamados "átomos gigantes".

 

3    Punto cuántico con varios electrones

Los niveles energéticos de partículas cargadas confinadas a un volumen finito pueden ser afectados principalmente por dos factores, el acoplamiento spin-órbita y la interacción de Coulomb entre partículas. Si la dimensión del volumen está dada por r, la relación entre la energía de interacción Coulombiana U ~ q²/4πε₀r y la energía cinética K ~ h²/mr² es, en unidades atómicas, U/K ~ r. En física nuclear r ~ 10^-5, por lo que en ese campo la interacción de Coulomb es secundaria y la corrección más importante viene del acoplamiento spin-órbita. En nuestro caso, en cambio, U/K ~ 1, lo que indica que se debe considerar la interacción de Coulomb con más detenimiento. En cuanto al acoplamiento spin-órbita, la física atómica nos enseña que este efecto es importante sólo para los estados en los que los electrones sufren un fuerte potencial Coulombiano, lo que normalmente no es el caso en un punto cuántico.

El Hamiltoniano de varios electrones en un punto cuántico está dado, entonces, por H = H₀ + H_I, donde H₀ es la suma de los Hamiltonianos libres de cada electrón y H_I es el término de interacción dado por

donde v es la repulsión Coulombiana entre electrones. En términos de los operadores de creación y destrucción correspondientes a la base introducida anteriormente, el operador Hamiltoniano libre es

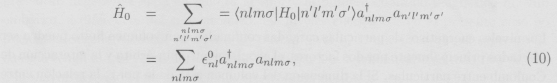
donde ε denota los niveles energéticos asociados a la base {φ_nlm}. El Hamiltoniano de interacción se escribe

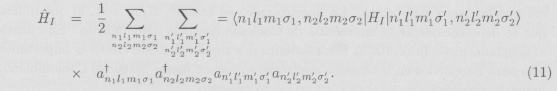
Los elementos de matriz de la interacción de Coulomb son importantes sólo cuando representan la interacción directa entre dos electrones y cuando éstos tienen spin opuesto. En efecto, aunque la interacción en sí es independiente del spin, el principio de exclusión de Pauli disminuye grandemente la interacción de Coulomb entre electrones de mismo spin. Como primera aproximación, en el presente trabajo consideramos un Hamiltoniano de interacción en el que la interacción directa U entre electrones de spin opuesto es la misma, es decir

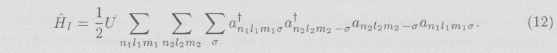
En el caso de una partícula de radio 20 Å, esto se cumple con buena aproximación, habiéndose encontrado numéricamente U = 0.078 Ry.

Para encontrar las energías del sistema en interacción debemos calcular la función de Green electrónica. Sea

donde es una función de Green a temperatura finita y w_n es una frecuencia de Matsubara fermiónica. Introduciendo la notación v = nlmσ, la función de Green para un electrón independiente, o libre, se escribe

donde ε = ε y μ es el potencial químico.

Dado que en nuestro caso U es mucho más pequeña que las energías de las partículas libres (ver Fig. 1), se puede tratar de calcular la función de Green en interacción de manera perturbativa. La ecuación de Dyson para es

donde Σ(v, iω_n) es la "self-energy" o "auto-energía". Se puede probar fácilmente que, al primer orden en U, la auto-energía es

donde σ es el spin asociado a v y N__σ es valor esperado para el operador número de partículas con spin -σ en el caso libre, i.e., N_σ = Σ_nlm ƒ_nmlσ, con f_nmlσ la función de ocupación libre. Puesto que la interacción U no es nula sólo para estados de spin opuesto, la auto-energía proviene de procesos de difusión directa. Los términos en los que una línea fermiónica es cerrada por una misma línea de interacción, no contribuyen. Tal es el caso de la difusión de intercambio. La función de Green en interacción al primer orden en U es entonces

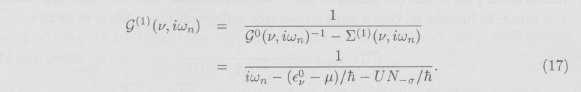
Finalmente, los niveles energéticos están dados por la función espectral A(E) que es proporcional a la parte imaginaria de la función de Green retardada G^R, i.e., la continuación analítica de para iω_n → E + iη . A temperatura nula, la función espectral se escribe

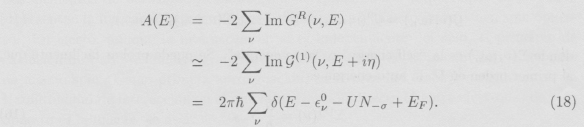
El número total de partículas, claro está, determina la energía de Fermi del sistema E_F = lim_T→0 μ

 

4    Resultados y discusión

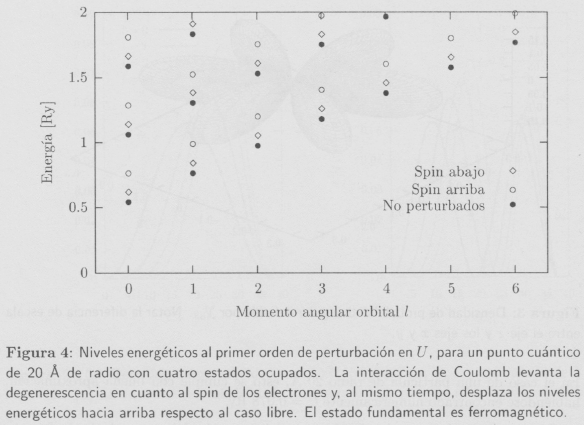
Se han calculado los niveles energéticos perturbados para una partícula de radio R= 20 Å. Se ha asumido que el estado fundamental del sistema libre obedece a las reglas de Hund [9], que relacionan el spin total S, el momento angular orbital L y el momento angular total J. Se ha considerado primero el caso de un punto cuántico con cuatro electrones. En este caso, el estado fundamental libre estaría dado por f_100↓, f_100↑, f_111↓ y f_110↓. (i.e., el nivel más bajo n = 1, l = 0 ocupado con dos electrones de spin opuesto, y dos electrones con spin abajo en el siguiente nivel, n = 1, l = 1, de acuerdo a las reglas de Hund). En la Fig. 4 se muestran los niveles energéticos perturbados para este caso. Se puede apreciar que la interacción de Coulomb levanta la degenerescencia de spin (aunque no la de número cuántico magnético m). Es así que se confirma que la interacción de Coulomb produce un estado fundamental ferromagnético estable cuando el sistema posee capas l incompletas. Por otra parte, en la misma figura se puede ver que los niveles energéticos se encuentran todos desplazados hacia arriba por la interacción de Coulomb respecto al caso libre, como era de esperar. En la figura se muestran también los niveles no-perturbados para mejor comparación.

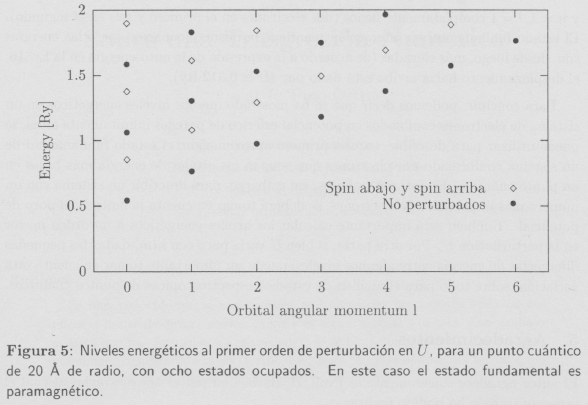
En caso de un estado fundamental no-perturbado paramagnético, es decir, en el que no existen capas l incompletas, la Ec. 16 nos indica que los niveles energéticos perturbados serán degenerados en cuanto al spin. Por esta razón, el estado fundamental en interacción será también paramagnético en este caso. Esto se ilustra en la Fig. 5, en la que se muestran los niveles energéticos perturbados para un sistema con ocho partículas. El estado fundamental no-perturbado está dado por los niveles n = 1, l = 0 y n = 1, l = 1 completamente llenos (dos electrones en el primero y seis en el segundo). El estado fundamental en interacción mantiene la misma ocupación, pero las energías son, desde luego, más elevadas (de acuerdo a la expresión de la auto-energía en la Ec. 16. el desplazamiento hacia arriba está dado por 4U 0.312 Ry).

Para concluir, podemos decir que se ha mostrado que los niveles energéticos de un sistema de electrones confinados en potencial esférico de paredes infinitamente altas, se puede utilizar para describir, en una primera aproximación, el estado fundamental de un sistema conformado por electrones que ocupan los niveles de energía más bajos en un punto cuántico. En futuros trabajos, sin embargo, para describir un sistema con un número más importante de electrones, se deberá tomar en cuenta la finitud del pozo de potencial. También será importante calcular los niveles energéticos a un orden mayor en la perturbación U. Por otra parte, si bien U varía poco con nlm, dadas las pequeñas diferencias de energía entre algunos niveles, puede ser importante tomar en cuenta esta variación, sobre todo para el análisis de estudios espectroscópicos de puntos cuánticos.

 

5    Agradecimientos

El autor agradece sinceramente al Prof. B. Barbiellini por el apoyo gracias al cual el presente trabajo ha podido realizarse.

 

Referencias

[1] M. R. Geller, cond-mat/0106256.        [ Links ]

[2] P. Butcher, N. H. March y M. P. Tosi, Eds., Physics of low dimensional semiconductor structures (Plenum Press, New York, 1993).

[3] G. Timp, Ed., Nanotechnology (Springer-Verlag, New York. 1999).

[4] Ver, por ejemplo, S. V. Gaponenko, Optical properties of semiconducting nanocrystals (Cambridge University Press, Cambridge, 1998).

[5] D. Loss y D. P. DiVincenzo, cond-mat/9701055.

[6] Xuedong Hu y S. Das Sarma, cond-mat/0102019.

[7] A. L. Fetter y J. D. Walecka, Quantum theory of many-particle systems (McGraw-Hill, New York, 1971).

[8] M. Abramowitz and I. Stegun, Handbook of mathematical functions (Dover, New York. 1965).

[9] N. W. Ashcroft y N. D. Mermin, Solid State Physics (Saunders Collego. New York. 1976).