https://doi.org/10.53287/hity1826bi37c

A.ARTÍCULOS

 

Localized two-dimensional patterns
morphology of a generalized nonlinear
Schrödinger equation

 

Morfología de patrones localizados bidimensionales
de una ecuación de Schrödinger no-lineal generalizada

 

 

DETERLINO URZAGASTI^†
Planetario Max Schreier, P.O.Box 316 4 Universidad Mayor de San Andrés,
La Paz, Bolivia
^† Email: durzagasti@fcpn.edu.bo.
Recibido 4 de diciembre de 2022     Aceptado 22 de diciembre de 2022

 

 

---

Resumen

Se realiza una clasificación morfológica cualitativa sobre una muestra de cientos de patrones bidimensionales encontrados al resolver numéricamente una ecuación nolineal generalizada de Schrödinger dentro de una región de parámetros donde coexisten estos patrones con soluciones homogéneas no triviales. Los patrones hallados van desde aquellos muy simples a otros más complejos. Aparte de la forma, cada patrón es caracterizado también por su contenido caótico. Asimismo se observa la interacción de los distintos tipos de patrones.

Descriptores: Ecuaciones de amplitud; dinámica disipativa; sistemas dinámicos; formación de patrones.

---

Código(s) PACS: 05.90.+m

---

Abstract

A qualitative morphological classification is performed on a sample of hundreds of two-dimensional patterns found by numerically solving a nonlinear generalized Schrödinger equation within a region of parameters where these patterns coexist with non-trivial homogeneous solutions. The patterns found range from those very simple to others more complex. Apart from the shape, each pattern is also characterized by its chaotic content. Likewise, the interaction of the different pattern types is observed.

Subject headings: Amplitude equations; dissipative dynamics; dynamical systems; pattern formation.

---

 

 

1  Introduction

Localized patterns in two dimensions, that is, of finite area, are observed in many physical contexts. To mention just a few, we can say that they are present in Bose-Einstein condensates as well as in optical, magnetic, and mechanical systems. Given the large number of works in this field, we will refer the reader to the publications  Aranson & Kramer, [2002], Dangelmayr & Oprea, [2004], Pismen, [2006] and references therein, where different qualitative and quantitative analyzes are presented, as well as their comparison with experimental results.

Some years ago, patterns in two dimensions that appear when a generalized nonlinear Schrödinger equation is solved numerically have been studied in depth ( ). The present manuscript presents results of a morphological analysis of a large set of simulations carried out solving the same equation and in the same region of parameters given in  Urzagasti et al., [2017].

The working equation for the complex amplitude A reads

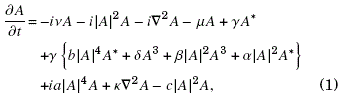
Details of the meaning of all terms can be found in  Urzagasti et al., [2017]. However, we can mention that it contains a dissipative term with coefficient µ, a detuning term to approach the parametric resonance, ν, and a forcing term, with coefficient γ. Regarding the other terms, we can highlight that the equation is rich in nonlinearity and this allows the coexistence of the structures that we seek to classify morphologically with the non-trivial homogeneous background.

Likewise, the connection with physics in different scenarios is given in detail in  Urzagasti et al., [2017]. This important aspect, that of the universality of the working equation, is the main motivation of this work.

 

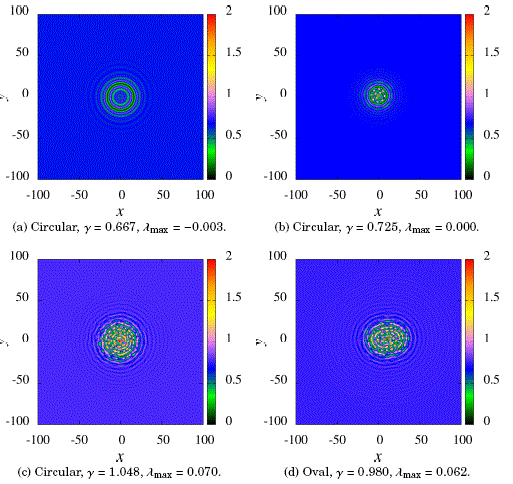
Figure 1: Localized circular-like patterns.

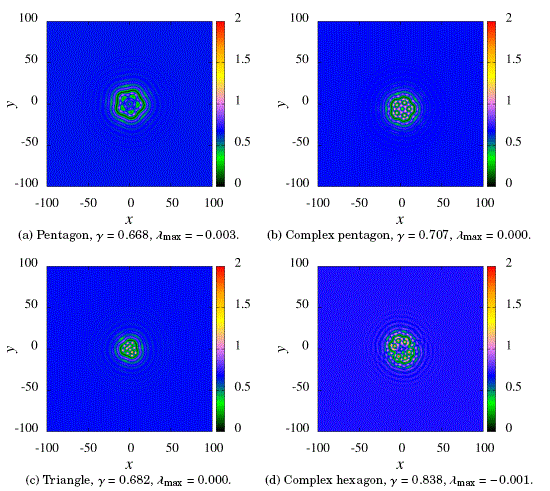
Figure 2: Localized regular patterns.

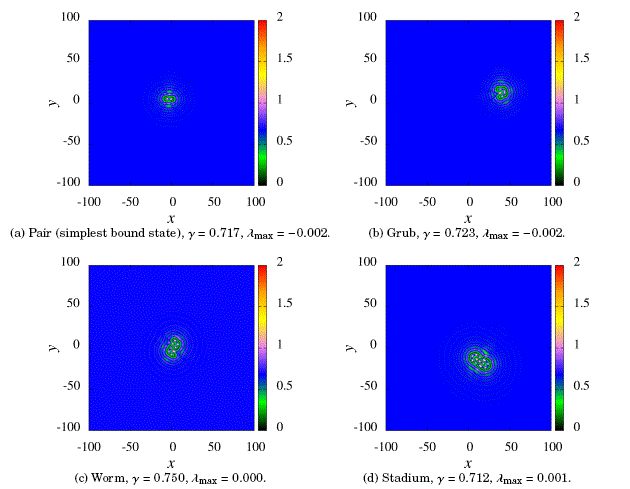
Figure 3: Localized chain-like patterns.

 

2  Results

We show some examples of the basic structures we have found in our simulations at ν = −0.05, for the detuning parameter, and for different values of the γ driving parameter after a simulation time interval of Δt=5.6×10³ has elapsed. We have worked 359 objects, for which we have performed some kind of basic morphological clasification by direct inspection of the final results. The initial condition for all the simulations was the same pulse with circular symmetry. All the figures below corresponding to these examples map with a color code the modulus of the amplitude (lAl) at the final instant. To determine the chaotic content, we use as an indicator the maximum Lyapunov exponent, λ_max, which is obtained numerically using the techniques described in  Urzagasti et al., [2017].

To begin, in Fig. 1 we show different circular-like structures. In the stationary regime these structures are isotropic, while in the quasi-stationary and chaotic cases they are clustered and composed of concentric chains of peaks. There are some exceptions to the circular shape as the oval object shown in box (d) of the same Figure.

In Fig. 2 we show some regular in shape patterns that are found in both the stationary and quasi-stationary regimes. In particular, the object shown in box (d) is an exceptional stationary case in the chaotic zone above γ = 0.8.

Figure 3 shows some simple chain-like structures. We point out that grub and stadium structures tend to move away from their initial position.

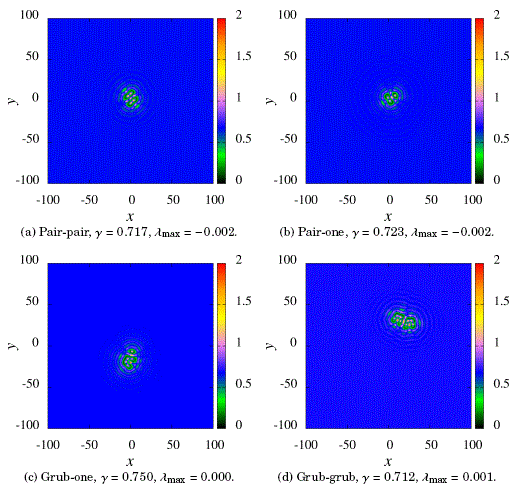
The simplest structures appear interacting for some parameters. Examples of the resulting clusters are shown in Fig. 4. Again, we remark how the structures involving grubs move away from the initial central position.

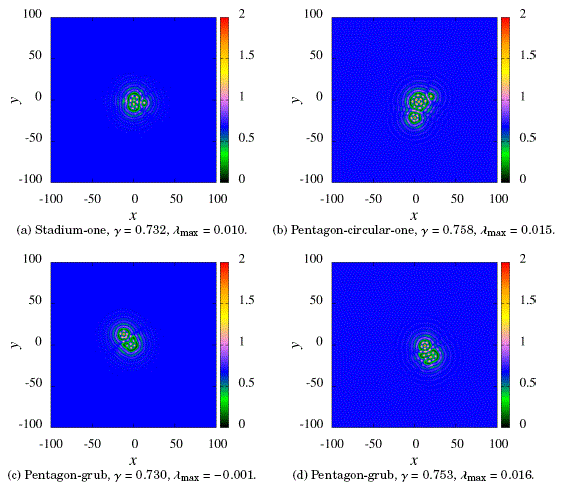
Also, there are interacting systems that involve more complex structures such as circles, pentagons, and stadiums. Some examples are shown in Fig. 5. Note that in the case of pentagon-grub structure there are a stationary version as well as a chaotic one.

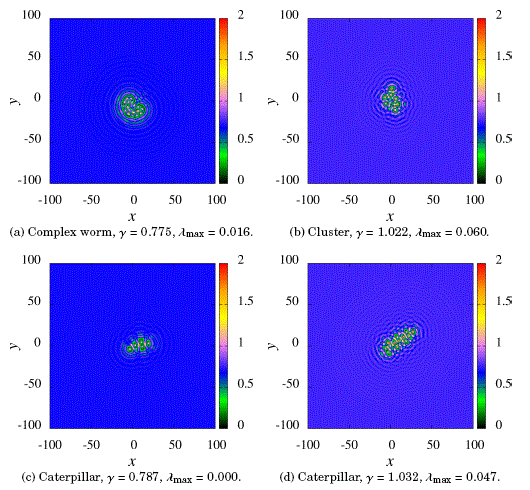
We found even more complex structures such as those shown in Fig. 6. We remark that the caterpillar structure appears in both the cuasistationary and chaotic cases.

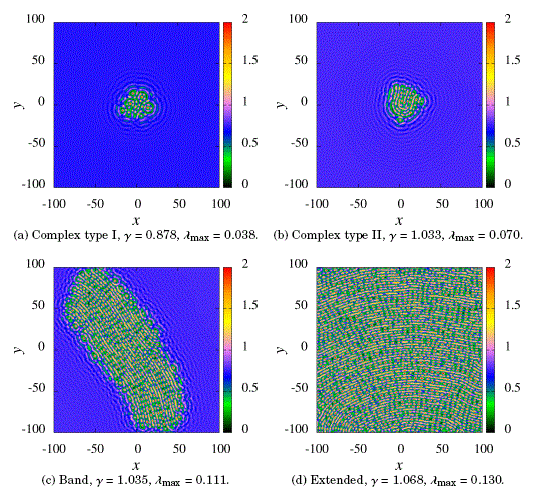
Finally, we distinguish two general types of big complexes: complex type I, which are composed of several kinds of interacting complexes shuch as the one shown in box (a) of Fig. 7, and complex type II which are built from several interacting chains of peaks and that have a tassel-like structure as it is shown in the example in box (b) of the same Figure. Figure 7 also shows the very big and very chaotic structures that appear as a band-like and extended pattern structures in box (c) and (d), respectively.

Figure 4: Localized clusters of simple patterns.

Figure 5: Localized clusters with more complex patterns.

Figure 6: Localized complexes.

Figure 7: Localized and extended big complexes.

 

3  Concluding remarks

In summary, we have found several types of structures whose complexity is determined by their extension and by their number of walls, trenches, and soliton pulses. After an exhaustive review of the results of hundreds of simulations, only a few types of structures were found, namely: circular, oval, triangular, pentagonal, and hexagonal patterns; bound states of solitons, grubs, worms, and caterpillars; stadiums, clusters; complex irregular structures (here called type I complexes), complex tassel-like structures (here called type II complexes), and bands, which are extensive band-shaped structures.

In general, the greater the complexity, the greater the chaotic content; however, there are exceptions. In particular, less complex structures can be both chaotic and periodic.

It should be noted that some less complex objects acquire movement. We do not have an explanation of the cause of this interesting effect, nor of the causes for the formation of different patterns for very close values of the forcing parameter. These problems, which are outside the scope of this manuscript, are raised for further study.

 

Conflicto de intereses

El autor declara que no hay conflicto de intereses respecto a la publicación de este documento.

 

References

[Aranson & Kramer 2002]

Aranson, I. S. & Kramer, L. 2002, Rev. Mod. Phys., 74, 99         [ Links ]

[Dangelmayr & Oprea 2004]

Dangelmayr, G. & Oprea, I. 2004, Dynamics and Bifurcation of Patterns in Dissipative Systems (WORLD SCIENTIFIC) Links ] Arial, Helvetica, sans-serif">

[Pismen 2006]

Pismen, L. M. 2006, Patterns and Interfaces in Dissipative Dynamics (Springer Berlin, Heidelberg) Links ] Arial, Helvetica, sans-serif">

[Urzagasti et al. 2017]

Urzagasti, D., Laroze, D., & Pleiner, H. 2017, Phys. Rev. E, 95, 052216         [ Links ]