Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física vol.39 no.39 La Paz dic. 2021
A. ARTÍCULOS
Dinámica de una partícula en una red de
enlace fuerte bajo un potencial coulombiano
The dynamics of a particle in a tight-binding
lattice under a coulomb potential
Javier Alejandro Velasco Villarroel![]() , Diego Sanjinés Castedo†
, Diego Sanjinés Castedo†![]()
Instituto de Investigaciones Físicas, Universidad Mayor de San Andrés Campus
Universitario, c. 27 Cota-Cota, Casilla de Correos 8635 La Paz - Bolivia
†diegosanjinescastedo@gmail.com
Recibido 10 de octubre de 2021 Aceptado 28 de noviembre de 2021
Resumen
Estudiamos la dinámica de enlace fuerte (tight-binding) de una partícula cargada que se mueve por el mecanismo de hopping en una red unidimensional, bajo el efecto de un potencial coulombiano debido a otra partícula inmóvil (impureza). La dinámica cuántica de la partícula se estudia por medio del método pseudo-espectral adaptado a un Hamiltoniano de enlace fuerte con interacciones a primeros vecinos; los resultados para los valores esperados de posición y velocidad se comparan con los obtenidos por el método semiclásico invocando al potencial efectivo en la red. Los resultados son notablemente similares cuando la partícula se encuentra lejos de la impureza pues allí el campo coulombiano es aproximadamente uniforme, mientras que cerca de la impureza los resultados difieren debido a la dispersión cuántica del paquete de ondas en presencia de un campo altamente inhomogéneo. Sin embargo, y de manera interesante, los resultados cuánticos y semiclásicos coinciden en el régimen del contínuo (relación de dispersión parabólica) debido a la transmisión del paquete de ondas a través de la impureza.
Descriptores: Modelo de enlace fuerte - método semiclásico - sistemas excitónicos.
Código(s) PACS: 31.15.aq - 03.65.Sq - 71.35.-y
Abstract
We study the tight-binding dynamics of a charged particle by the hopping mechanism in a one - dimensional lattice under the action of a Coulomb potential due to another fixed particle (impurity). The quantum dynamics is studied using the pseudo-spectral method applied to a tight-binding Hamiltonian with nearest neighbors interactions. The resulting expected values for position and velocity are then compared with those deduced by the semi-classical method invoking the effective potential in the lattice. These results are notably similar when the particle is located far from the impurity position since the Coulomb field is approximately uniform, while when near to the impurity the results are different due to the quantum dispersion of the particle's wavepacket under a highly inhomogeneous field. Interestingly, however, the quantum and semiclassical results coincide in the continuous regime (parabolic dispersion relation) due to the transmission of the particle's wavepacket through the impurity.
Subject headings: Tight-binding model - semiclassical method - excitonic systems.
1. Introducción
El problema de Coulomb en una red (unidimensional) se refiere en este trabajo a las características del movimiento de una partícula con carga eléctrica q en presencia de un campo Coulombiano con energía potencial V(x)=–V0/x, provocado por otra partícula (impureza) con carga eléctrica Q que se encuentra fija en x=0. Invocamos el modelo de enlace fuerte (tight-binding) para describir el movimiento de la primera partícula por el mecanismo de hopping.
Este problema es relevante, por ejemplo, en la física de procesos excitónicos en cristales moleculares ([ 1961 Merrifield , 1980 Nakijama et al. ]) y en la teoría de muchos cuerpos del excitón de Hu-bbard fuertemente acoplado ([ 1979 Gallinar , 1978 Hubbard ]). En [ 1984 Gallinar ] se calcula el espectro energético usando la técnica de las funciones de Green. Asímismo, en [ 1992 Kvitsinsky ] se resuelve de manera exacta el problema cuántico para los estados estacionarios de la partícula en una red unidimensional, dichas eigenfunciones se expresan en términos de funciones hipergeométricas. En [ 2016 Petrova y Moesnner ] se amplía el resultado obtenido por [ 1984 Gallinar ] y se muestra una solución analítica completa para el espectro de e-nergías en el caso de la red de Bethe. En la mayoría de las aplicaciones referidas en [ 2016 Petrova y Moesnner , 2016 Burgess , 2021 Wang et al. ] es posible obtener información relevante a partir del espectro energético y la densidad de estados que es importante, entre otros, para la determinación del espectro debido a impurezas, lo que permite comprender cómo modificar la brecha de un material a fin de controlar las propiedades de conducción eléctrica.
Si bien en la mayoría de las referencias citadas se atiende la cuestión de determinar el espectro energético, no encontramos -hasta donde pudimos averiguar- los casos donde se muestre de manera explícita la dinámica de la partícula. Existe riqueza física en el análisis de la evolución temporal del paquete de ondas, que es un problema derivado del estudio de los efectos de una impureza en una red, como en el estudio del excitón, ([ 1961 Merrifield ]) los antiferromagnetos ([ 2016 Petrova y Moesnner ]) y la localización de Anderson.([ 2016 Petrova y Moesnner ]) De hecho, en [ 2016 Petrova y Moesnner ] se menciona que el estudio de la evolución temporal de una partícula en la red de Bethe puede servir como base para estudiar de manera aproximada la dispersión de una partícula en "hielo cuántico". En el caso del excitón, el tiempo de vida media para la recombinación es del orden de nanosegundos; ([ 1980 Nakijama et al. ]) si el periodo de la oscilación del electrón (considerando que el hueco está fijo) resulta ser menor a dicho tiempo de recombinación, entonces la evolución temporal del estado electrónico es relevante para describir las propiedades de transporte eléctrico pues permite prever un posible escenario experimental para detectar la radiación de dipolo asociada a dicha oscilación.
Nuestro trabajo está organizado de la siguiente forma: en la Sección 2 se desarrolla el formalismo cuántico y la aproximación semiclásica relevantes para esta investigación; en la Sección 3 se presenta dos casos de estudio numéricos correspondientes a la evolución de la partícula en regiones lejanas y cercanas a la impureza; en la sección 4 se desarrolla la aproximación de la dinámica en el régimen del continuo. Finalmente, en la sección 5 se resume las conclusiones más relevantes y algunas posibles orientaciones.
2 Formalismo cuántico y modelo semiclásico
El Hamiltoniano cuántico de enlace fuerte para una partícula con carga eléctrica q moviéndose en una red con constante reticular a por el mecanismo de hopping y bajo el efecto de un potencial Coulombiano Vn = –V0/ l na l es
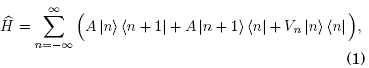
donde A es el elemento de salto entre sitios vecinos de la red; V0/(Kq2)=Q/q indica el valor de la carga eléctrica Q (localizada en n=0) en múltiplos de q. La solución de la ecuación de Schrödinger ![]() en la base de funciones de Wannier es el estado normalizado
en la base de funciones de Wannier es el estado normalizado
![]()
tal que ![]() . El centroide del paquete de ondas es
. El centroide del paquete de ondas es ![]() y su velocidad es
y su velocidad es ![]() , donde x = an se proyectó en el subespacio discreto de la red. La aplicación del método pseudo-espectral en una banda ([ 1999 Sanjines y Gallinar ]) conduce a la fórmula i-terativa para los coeficientes cn(t):
, donde x = an se proyectó en el subespacio discreto de la red. La aplicación del método pseudo-espectral en una banda ([ 1999 Sanjines y Gallinar ]) conduce a la fórmula i-terativa para los coeficientes cn(t):
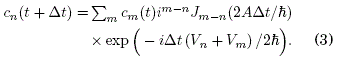
La singularidad debida a Vn = –V0/l na l si n=0 se evita haciendo que c0 = 0 en (3); esta anulación no representa un peso estadístico significativo en la distribución de probabilidad del paquete, por lo que su evolución subsecuente queda prácticamente inalterada. La energía correspondiente al estado lΨ⟩ es ![]() , donde los valores espe-rados de las energías cinética y potencial son:
, donde los valores espe-rados de las energías cinética y potencial son:
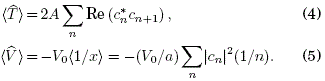
La energía potencial ⟨V⟩ se puede expresar en términos de los momentos estadísticos de una distribución de probabilidad, W(t) (valor cuadrático medio), S(t) (sesgo) y K(t) (curtosis), definidos con respecto al centroide o valor medio del paquete de ondas como:
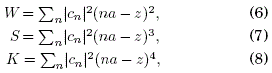
de tal forma que
![]()
donde
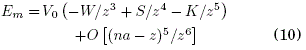
se define como la "energía de los momentos estadísticos".
A continuación aplicamos el método semiclásico al estudio del problema propuesto en este trabajo. Una justificación concisa y pedagógica de dicho método al caso de un potencial periódico en general se puede encontrar, por ejemplo, en el Cap. 12 de [ 1976 Ashcroft y Mermin ].
La evolución de la posición x y el momentum cristalino k está dada por las ecuaciones de Hamilton:
![]()
donde la energía total E es igual al valor de la función hamiltoniana H(x,k) que se construye como
![]()
a partir de la estructura de banda ε(k)=2A(1–cosak) correspondiente al Hamiltoniano libre H0 en (1) con Vn=0, i.e., ![]() , siendo lk⟩ los estados de Bloch. Siguiendo a [1976 Ashcroft y Mermin ] en la descripción semiclásica de la dinámica electrónica, la velocidad v(k) y la masa efectiva m(k) están dadas en función a la energía de la banda ε(k) como
, siendo lk⟩ los estados de Bloch. Siguiendo a [1976 Ashcroft y Mermin ] en la descripción semiclásica de la dinámica electrónica, la velocidad v(k) y la masa efectiva m(k) están dadas en función a la energía de la banda ε(k) como
![]()
Así, para la partícula que está inicialmente en reposo, ![]() . Luego, se define el potencial efectivo Vef(x) y la masa efectiva m en la red por
. Luego, se define el potencial efectivo Vef(x) y la masa efectiva m en la red por
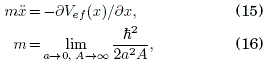
de donde se obtiene ([ 2014 Martínez et al. ])
![]()
Así, para el caso del potencial coulombiano V(x)=–V0/ l x l considerado en este trabajo, donde la partícula se encuentra inicialmente en reposo en la posición x0, la ec. (15) se puede integrar para obtener la ecuación de la trayectoria en el espacio ![]() :
:
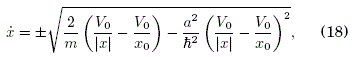
donde la función par x(x) está definida en el dominio ![]() . Para x > 0 se obtienen los intervalos (xr,x0) para la posición y (–vm,vm) para la velocidad, donde
. Para x > 0 se obtienen los intervalos (xr,x0) para la posición y (–vm,vm) para la velocidad, donde
![]()
El periodo τ de una órbita de la trayectoria en el espacio ![]() se calcula de (18) como
se calcula de (18) como
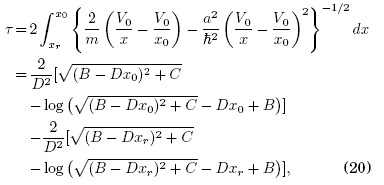
con coeficientes B,C,D que dependen de los parámetros a,m,x0,V0.
3 Casos de estudio
Se muestran a continuación los resultados de dos casos de estudio. El primero se elegió de tal forma que el movimiento de la partícula se realice "lejos" de la impureza comenzando en el sitio n=x0/a=2500 y con una relación de cargas Q/q = 120000. El segundo caso se elegió de tal forma que el movimiento se realice "cerca" de la impureza comenzando en el sitio n=x0/a=50 y con una relación de cargas Q/q = 100. En todos los casos el paquete de ondas inicial es gaussiano:
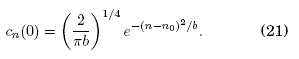
3.1 Caso de la dinámica "lejana"
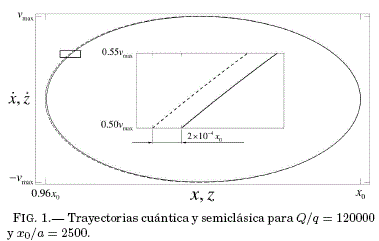
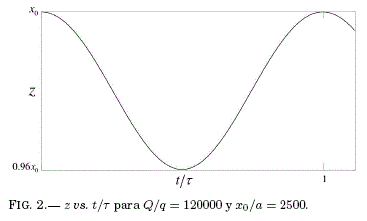
En la Fig. 1 se muestra las trayectorias superpuestas en los espacios (z, ·z) y ![]() . Puede verse que las trayectorias cuántica y semiclásica prácticamente coinciden. En la Fig. 2 se muestra la gráfica de z(t). A fin de cuantificar dicha coincidencia se definen las siguientes cantidades:
. Puede verse que las trayectorias cuántica y semiclásica prácticamente coinciden. En la Fig. 2 se muestra la gráfica de z(t). A fin de cuantificar dicha coincidencia se definen las siguientes cantidades:
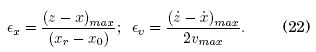
Los valores que se obtiene son εx = 0.40 % y εv = 0.22 %, lo que confirma la buena coincidencia de los resultados cuántico y semiclásico.
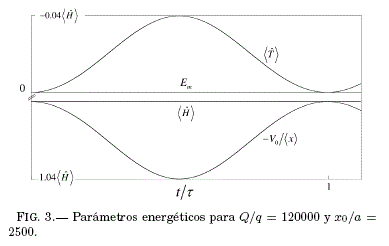
Para estudiar los parámetros energéticos desde el modelo cuántico, se realiza la gráfica de la evolución temporal de ![]() y Em. En la Fig. 3 puede verse que el valor de Em es muy pequeño y por lo tanto no tiene efecto sobre la dinámica de la partícula; los términos de energía
y Em. En la Fig. 3 puede verse que el valor de Em es muy pequeño y por lo tanto no tiene efecto sobre la dinámica de la partícula; los términos de energía ![]() tienen un comportamiento análogo al predicho mediante el modelo semiclásico. Dado que el aporte de Em es casi nulo, se puede decir que durante el movimiento la energía total se distribuye entre los términos
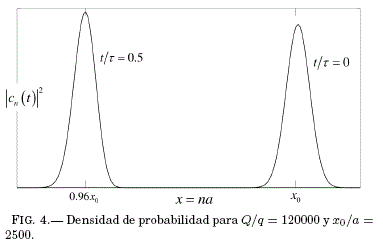
tienen un comportamiento análogo al predicho mediante el modelo semiclásico. Dado que el aporte de Em es casi nulo, se puede decir que durante el movimiento la energía total se distribuye entre los términos ![]() . La Fig. 4 muestra la evolución del paquete de ondas a través de l cn(t)2 l. Puede verse que el paquete mantiene su forma gaussiana y se va deformando muy poco. Así, el valor del sesgo a lo largo del tiempo es muy pequeño mientras el valor cuadrático medio y la curtosis varían muy poco, como debe ser si el valor de Em es muy pequeño. Este caso corresponde al fenómeno conocido de la oscilación de Bloch ([ 2004 Hartmann et al. ]) y es el resultado de la evolución de un paquete de ondas en presencia de un campo externo homogéneo, lo que se cumple aproximadamente para el campo Coulombiano de la impureza en la región "lejana".
. La Fig. 4 muestra la evolución del paquete de ondas a través de l cn(t)2 l. Puede verse que el paquete mantiene su forma gaussiana y se va deformando muy poco. Así, el valor del sesgo a lo largo del tiempo es muy pequeño mientras el valor cuadrático medio y la curtosis varían muy poco, como debe ser si el valor de Em es muy pequeño. Este caso corresponde al fenómeno conocido de la oscilación de Bloch ([ 2004 Hartmann et al. ]) y es el resultado de la evolución de un paquete de ondas en presencia de un campo externo homogéneo, lo que se cumple aproximadamente para el campo Coulombiano de la impureza en la región "lejana".
3.2 Caso de la dinámica "cercana"
En la Fig. 5 se muestra una comparación entre la trayectoria cuántica (línea sólida) en el espacio (z,·z) y la trayectoria semiclásica (línea segmentada) en el espacio ![]() . Los valores εx = 9.20 % y εvel = 8.20 % indican la discrepancia entre ambas trayectorias lo que se aprecia en el hecho de que la trayectoria cuántica no se cierre.
. Los valores εx = 9.20 % y εvel = 8.20 % indican la discrepancia entre ambas trayectorias lo que se aprecia en el hecho de que la trayectoria cuántica no se cierre.
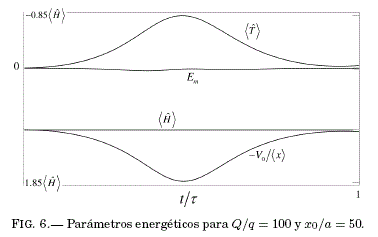
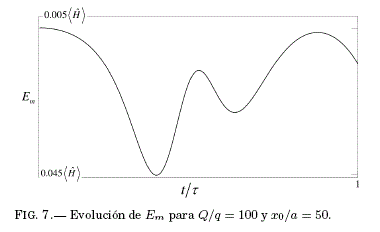
El origen de esta discrepancia numérica se halla en las ecs. (9) y (10) para ![]() , respectivamente. Durante el ciclo de la Fig. 5 los valores de z se encuentran cerca del sitio x = 0 de la impureza, donde el valor de Em se vuelve relevante (Fig. 7) y la energía total se distribuye entre los términos
, respectivamente. Durante el ciclo de la Fig. 5 los valores de z se encuentran cerca del sitio x = 0 de la impureza, donde el valor de Em se vuelve relevante (Fig. 7) y la energía total se distribuye entre los términos ![]() y Em. Como consecuencia de la relevancia del término Em, el valor de la energía total se mantiene constante en cualquier instante pues los otros dos términos adoptan valores menores a sus correspondientes semiclásicos (Fig. 6), lo cual explica que los valores de z y · z sean menores que x y ·x.
y Em. Como consecuencia de la relevancia del término Em, el valor de la energía total se mantiene constante en cualquier instante pues los otros dos términos adoptan valores menores a sus correspondientes semiclásicos (Fig. 6), lo cual explica que los valores de z y · z sean menores que x y ·x.
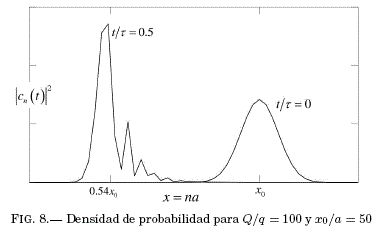
Así, cuando el paquete de ondas se mueve cerca de la impureza, los términos de la energía asociados a los momentos estadísticos son significativos y se ven "revelados" debido a la extensión del paquete en presencia del campo coulombiano inhomogéneo. En la Fig. 8 se muestra la evolución de la densidad de pro-babilidad del paquete de ondas para t = 0 y t = τ/2. De nuevo, la deformación del paquete está asociada al aumento del valor de los momentos estadísticos con energía Em.
4 Transición al régimen del continuo
La transición al régimen del continuo se realiza mediante los límites ![]() considerados en la ec. (16) donde se definió la masa efectiva. En la Tabla 1 se muestran las variables relevantes en dicho régimen.
considerados en la ec. (16) donde se definió la masa efectiva. En la Tabla 1 se muestran las variables relevantes en dicho régimen.
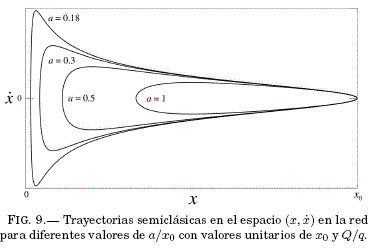
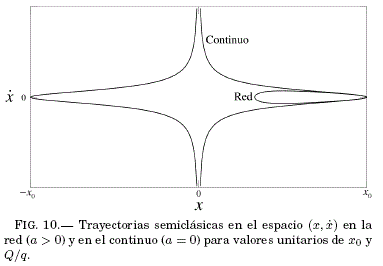
En la Fig. 9 se muestra las trayectorias en el espacio ![]() correspondientes a diferentes valores de a/x0 de tal forma que en todos los casos el sitio inicial de la red es el mismo. Puede verse que a medida que
correspondientes a diferentes valores de a/x0 de tal forma que en todos los casos el sitio inicial de la red es el mismo. Puede verse que a medida que ![]() , el valor de la velocidad máxima es cada vez mayor mientras el punto de retorno se aproxima cada vez más al origen. En la Fig. 10 se muestran las trayectorias semiclásicas para el caso de la red (a > 0) y del continuo (a = 0). Ya que la velocidad semiclásica
, el valor de la velocidad máxima es cada vez mayor mientras el punto de retorno se aproxima cada vez más al origen. En la Fig. 10 se muestran las trayectorias semiclásicas para el caso de la red (a > 0) y del continuo (a = 0). Ya que la velocidad semiclásica ![]() en (18) diverge en x = 0, y dado que las ecs. de Hamilton (11) son compatibles con la ec. de Schrödinger no-relativista, invocaremos un mecanismo cuántico para justificar el "salto" de la partícula a través de la discontinuidad de
en (18) diverge en x = 0, y dado que las ecs. de Hamilton (11) son compatibles con la ec. de Schrödinger no-relativista, invocaremos un mecanismo cuántico para justificar el "salto" de la partícula a través de la discontinuidad de ![]() en x = 0, de tal forma que la velocidad se mantenga constante y dentro del límite no-relativista durante dicho "salto", esto es,
en x = 0, de tal forma que la velocidad se mantenga constante y dentro del límite no-relativista durante dicho "salto", esto es, ![]() . Así, por dicho mecanismo, la posición de la partícula oscilaría periódicamente en el intervalo (– l x0 l , l x0 l) trasmitiéndose a través de la impureza localizada en x=0.
. Así, por dicho mecanismo, la posición de la partícula oscilaría periódicamente en el intervalo (– l x0 l , l x0 l) trasmitiéndose a través de la impureza localizada en x=0.

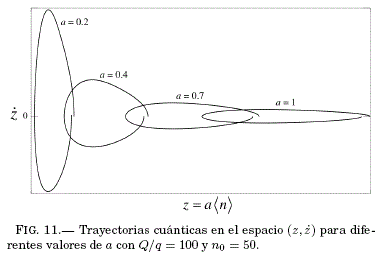
La Fig. 11 muestra las trayectorias cuánticas en el espacio ![]() correspondientes a las de la Fig. 9 para diferentes valores de a; en todos los casos la partícula es liberada desde el mismo sitio n0 = 50. A medida que
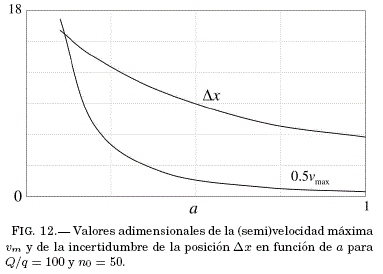
correspondientes a las de la Fig. 9 para diferentes valores de a; en todos los casos la partícula es liberada desde el mismo sitio n0 = 50. A medida que ![]() , el valor de la velocidad máxima aumenta mientras la partícula se acerca a la impureza. En la Fig. 12 se muestran los valores adimensionales de la (semi)velocidad máxima y la incertidumbre en la posición
, el valor de la velocidad máxima aumenta mientras la partícula se acerca a la impureza. En la Fig. 12 se muestran los valores adimensionales de la (semi)velocidad máxima y la incertidumbre en la posición ![]() en el sitio donde ocurre esa velocidad máxima.
en el sitio donde ocurre esa velocidad máxima.
Estos resultados sugieren invocar un principio de incertidumbre en la red expresado por ![]() (con
(con ![]() ), como el referido mecanismo de "salto" de la partícula. Esto es, a medida que
), como el referido mecanismo de "salto" de la partícula. Esto es, a medida que ![]() , el valor de Δx aumenta, así que necesariamente el valor de Δk debe disminuir. Luego, el paquete de ondas se transmite a través de la impureza en x=0, manteniendo aproximadamente el mismo valor de la velocidad
, el valor de Δx aumenta, así que necesariamente el valor de Δk debe disminuir. Luego, el paquete de ondas se transmite a través de la impureza en x=0, manteniendo aproximadamente el mismo valor de la velocidad ![]() . Este salto no ocurre entre las posiciones x y –x lejos de la impureza ya que el valor de Δx no es suficientemente grande como para satisfacer la condición
. Este salto no ocurre entre las posiciones x y –x lejos de la impureza ya que el valor de Δx no es suficientemente grande como para satisfacer la condición ![]() de manera consistente con el mecanismo de salto sugerido por la trayectoria en el continuo en la Fig. 10. El "rebote" de la partícula descrito por la transición
de manera consistente con el mecanismo de salto sugerido por la trayectoria en el continuo en la Fig. 10. El "rebote" de la partícula descrito por la transición ![]() en el sitio x=0+ (Figs. 9 y 11) correspondería a la expresión
en el sitio x=0+ (Figs. 9 y 11) correspondería a la expresión ![]() dada la gran aceleración que experimentaría la partícula en comparación a la de su transmisión a través de la impureza. Este caso no se puede describir con el modelo físico supuesto en este trabajo dado por el hamiltoniano conservativo H en la ec. (1).
dada la gran aceleración que experimentaría la partícula en comparación a la de su transmisión a través de la impureza. Este caso no se puede describir con el modelo físico supuesto en este trabajo dado por el hamiltoniano conservativo H en la ec. (1).
Así, y dentro de los límites de validez de dicho modelo físico, el referido principio de incertidumbre en la red que justifica la transmisión de la partícula a través de la impureza (![]() ) cuando la partícula está cerca y lejos de la impureza, respectivamente), no supone una transición abrupta entre las probabilidades de transmisión a medida que la partícula se acerca a la impureza.
) cuando la partícula está cerca y lejos de la impureza, respectivamente), no supone una transición abrupta entre las probabilidades de transmisión a medida que la partícula se acerca a la impureza.
5 Conclusiones, interpretación y perspectivas
En este trabajo se estudió el problema de Coulomb en una red (unidimensional) referido a la dinámica de una partícula cargada en presencia del campo eléctrico provocado por otra partícula (impureza) que se encuentra fija en la red. Invocamos el modelo de enlace fuerte (tight-binding) para describir el movimiento de la primera partícula por el mecanismo de hopping. La integración temporal de la ecuación de Schrödinger se realizó por el método pseudo-espectral adaptado al caso del hamiltoniano de enlace fuerte con una energía potencial coulombiana y un paquete de ondas inicial gaussiano. Por otra parte, se aplicó asimismo la apro-ximación semiclásica por medio de las ecuaciones de movimiento de Hamilton a una función hamiltoniana construida a partir del espectro cuántico de la partícula libre para estados de Bloch y la e-nergía potencial coulombiana; se invocó la definición de la masa efectiva en términos de la 2da ley de Newton para deducir parámetros de las trayectorias semiclásicas a partir de un potencial efectivo. En el problema considerado en este trabajo la coincidencia entre los resultados cuánticos y semiclásicos es razonablemente buena y permite dilucidar aspectos relevantes de la dinámica del paquete de ondas.
Esos resultados referidos corresponden a dos casos: la dinámica "lejana" y la dinámica "cercana", especificadas así dependiendo de la separación entre la posición de la impureza y la posición inicial de la partícula. En el primer caso se verificó que la partícula efectúa aproximadamente oscilaciones de Bloch, como era de esperar en vista de la cuasi-homogeneidad del campo coulombiano en esa región "lejana" (Figs. 1-4). En el segundo caso los términos de la energía total correspondientes a los momentos estadísticos son relevantes y la deformación del paquete de ondas es significativa cerca de la impureza, lo que está asociado a la inhomogeneidad del campo coulombiano es esa región (Figs. 5-8).
A fin de contrastar aún los resultados cuánticos y semiclásicos, se invocó el límite del contínuo de manera consistente con la aproximación de masa efectiva definida en la ec. (16). La solución semiclásica no es contínua en dicho límite dada la divergencia de ![]() lo que supone la transición abrupta de la velocidad
lo que supone la transición abrupta de la velocidad ![]() en un intervalo espacial muy pequeño, es decir, la partícula "rebota" en la impureza. Pero este escenario físico es improbable bajo el modelo físico dado por el hamiltoniano conservativo H en la ec. (1) pues la aceleración de la partícula es muy grande como para ignorar la e-nergía del pulso electromagnético generado en tal "rebote". Así, la otra posible solución continua de la ec. (18) para (x,· x) en la región x < 0 se puede entender como una consecuencia semiclásica del principio de incertidumbre en la red, esto es, vm se mantiene aproximadamente constante
en un intervalo espacial muy pequeño, es decir, la partícula "rebota" en la impureza. Pero este escenario físico es improbable bajo el modelo físico dado por el hamiltoniano conservativo H en la ec. (1) pues la aceleración de la partícula es muy grande como para ignorar la e-nergía del pulso electromagnético generado en tal "rebote". Así, la otra posible solución continua de la ec. (18) para (x,· x) en la región x < 0 se puede entender como una consecuencia semiclásica del principio de incertidumbre en la red, esto es, vm se mantiene aproximadamente constante ![]() cuando el paquete está muy deformado cerca de la impureza, de tal forma que
cuando el paquete está muy deformado cerca de la impureza, de tal forma que ![]() . Luego, la transmisión de la partícula a través de la impureza y su posterior movimiento en la región x < 0 no involucra grandes valores de la aceleración, pero ya que el movimiento es periódico entre los extremos ±x0 entonces habrá una radiación de dipolo de baja energía que podría detectarse por las técnicas convecionales que se usan para observar la oscilación de Bloch.
. Luego, la transmisión de la partícula a través de la impureza y su posterior movimiento en la región x < 0 no involucra grandes valores de la aceleración, pero ya que el movimiento es periódico entre los extremos ±x0 entonces habrá una radiación de dipolo de baja energía que podría detectarse por las técnicas convecionales que se usan para observar la oscilación de Bloch.
Los casos estudiados en este trabajo pueden ser relevantes, por ejemplo, para estudiar la dinámica de un electrón en un sistema electrón-hueco (excitón) en una red, donde el hueco (impureza) se encuentra aproximadamente fijo debido a su mayor masa efectiva. El periodo de la oscilación para el caso del "rebote" del electrón (región 0 < x < x0) calculado en la ec. (20) es del orden del periodo de la oscilación de Bloch, ![]() s, mientras que el periodo en el caso de la transmisión a través del hueco es 2 τ. Por otra parte, el tiempo de recombinación típico de un excitón en cristales moleculares es del orden de 10–9 s, por lo que se producen unas 104 oscilaciones del electrón durante un régimen transitorio antes de la recombinación, lo que podría permitir hacer observaciones (a través de la radiación de dipolo) para dilucidar si el electrón rebota, o se transmite, o acaso rebota y se transmite, lo que seguramente arrojará resultados interesantes sobre la física de este tipo de fenómenos.
s, mientras que el periodo en el caso de la transmisión a través del hueco es 2 τ. Por otra parte, el tiempo de recombinación típico de un excitón en cristales moleculares es del orden de 10–9 s, por lo que se producen unas 104 oscilaciones del electrón durante un régimen transitorio antes de la recombinación, lo que podría permitir hacer observaciones (a través de la radiación de dipolo) para dilucidar si el electrón rebota, o se transmite, o acaso rebota y se transmite, lo que seguramente arrojará resultados interesantes sobre la física de este tipo de fenómenos.
Conflicto de intereses
Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.
References
Ashcroft N. & Mermin N. D. (1976) Solid State Physics (Saunders College, Philadelphia). [ Links ]
Burgess C. (2016) Coulomb potential on a lattice using graph theory, Tesis de Maestría en Física, Universidad de California, Santa Bárbara, USA. [ Links ]
Gallinar J.-P. (1979) "Quasi one dimensional conductors II", p. 105, Springer Lecture Notes in Physics, vol. 96, Springer, Berlin. [ Links ]
Gallinar J.-P. (1984) Phys. Lett. A, 103, 72. [ Links ]
Hartmann T., Keck F., Korsch H. J. & Mossmann S. (2004) New J. Phys. 6, 2. [ Links ]
Hubbard J. (1978) Phys. Rev. B 47, 494. [ Links ]
Kvitsinsky A. (1992) J. of Phys. A 25, 65. [ Links ]
Martínez L. A., Sanjinés D. & Gallinar J.-P. (2014) Int. J. Mod. Phys. B 28, 1450173. [ Links ]
Merrifield R. (1961) J. of Chem. Phys. 34: 1835-1839. [ Links ]
Nakajima S., Toyozawa Y. & Abe R. (1980) "The Physics of Elementary Excitations", Springer Series in Solid State Sciences, vol. 12, Springer, Berlin. [ Links ]
Petrova O. & Moesnner R. (2016) Phys. Rev. E 93, 012115. [ Links ]
Sanjines D. & Gallinar J.-P. (1999) J. Phys. Cond. Matter 11, 3729-3742. (2001) Phys. Rev. B 64, 054301. [ Links ]
Wang J., Van Pottelberge R., Zhao W. & Peeters F. (2021) arXiv e-prints, 2021, p. arXiv: 2105.05065. [ Links ]