Services on Demand
Journal
Article
Indicators
-
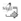 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
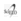 Similars in
SciELO
Similars in
SciELO
Share
Revista Boliviana de Física
On-line version ISSN 1562-3823
Revista Boliviana de Física vol.38 no.38 La Paz Nov. 2021
A. ARTÍCULOS
Effective Hamiltonian for a tight-binding square lattice and its relation
to a two-mesh LC circuit with discrete charge
Hamiltoniano efectivo de una red cuadrada de enlace fuerte y su relación con un
circuito LC de dos mallas con carga discreta
Evaristo Mamani C.![]() , Marcelo Calcina-Nogales
, Marcelo Calcina-Nogales ![]() , Diego Sanjinés Castedo
, Diego Sanjinés Castedo![]() †
†
Instituto de Investigaciones Físicas, Universidad Mayor de San Andrés
Campus Universitario, c. 27 Cota-Cota, Casilla de Correos 8635
La Paz - Bolivia
†diegosanjinescastedo@gmail.com
Recibido 2 de septiembre de 2021; aceptado 18 de noviembre de 2021
Resumen
En este trabajo consideramos una función hamiltoniana de enlace fuerte extendida a primeros y segundos vecinos para una partícula cargada que se transporta por saltos (hopping) en una red cuadrada en presencia de un campo estático arbitrario y un campo uniforme rápidamente oscilante con frecuencia ω. La aplicación del método semiclásico y el método de Kapitza de promediación temporal hasta O(ω-2) conduce a una función hamiltoniana efectiva (independiente del tiempo) con elementos de salto que dependen de los parámetros de los campos externos. Controlando dichos parámetros podemos manipular las interacciones de tal forma de emular un sistema físico diferente, en este caso, un circuito LC de dos mallas con carga discreta.
Descriptores: Método de enlace fuerte - modelo semiclásico - sistemas mesoscópicos.
Código(s) PACS: 31.15.aq, 03.65.Sq , 73.23.-b
Abstract
We consider an extended tight-binding Hamiltonian function comprising nearest and next-to-nearest neighbor interactions for a charged particle hopping in a square lattice in the presence of a static arbitrary field and a rapidly oscillating uniform field with frequency ω. The application of the semiclassical method and the Kapitza's method for time-averaging up to O(ω-2) yields an effective (time independent) Hamiltonian function with long range hopping elements that depend on the parameters of the external fields. By controlling these parameters we can engineer the interactions in such a way as to emulate a different physical system, namely, a two-mesh LC circuit with discrete charge.
Subject headings: Tight-binding method - semiclassical model - mesoscopic systems.
1. Introduction
The study of effective Hamiltonians in solid state physics, derived with time-averaging procedures (originally due to P. L. Kapitza for the study of the inverted pendulum Kapitza, [1965,Landau, [1985] applied to tight-binding lattices, has recently acquired interest given the feasibility of managing (engineering) the hopping elements when the lattice is subject to external and rapidly oscillating driving fields. Some of the effects relevant for transport phenomena include, for example: dynamic localization, coherent control of tunneling, metal-insulator transitions, atomic motion in atom traps, effective next-to-nearest neighbor interactions and effective Bloch oscillation Dunlap, [1986,Rahav, [2003,Bandyopadhyay, [2008,Itin, [2014,Itin, [2015,Mamani, [2017]. The idea of using an extended tight-binding Hamiltonian with a kinetic energy of the form ![]() can be traced back to the work of Dunlap and Kenkre, Dunlap, [1986] where their results concerning dynamic localization are extended to long-range interactions in a 1D lattice with hopping elements An and lattice constant a. The case where all the interactions are considered led to the new concept of exact dynamic localization in the presence of an AC electric field Dignam, [2002]. Such a concept of "band engineering" with long-range interactions has been also investigated (theoretically and experimentally1 in optical lattices; Longhi, [2010,Madison et al., [1998] reported the first observation of dynamical suppression of the band due to an external AC field in an optical lattice whereby the bandwidth shrinks to zero and the Bloch states become localized when the field amplitude meets a condition that was also derived in Mamani et al. Mamani, [2017] using the semiclassical method.2 More recent investigations in layered graphene systems show that the effects derived from an extended tight-binding Hamiltonian can be considered as improvements to the usual nearest neighbor model results Reich, [2002,Kundu, [2011,Wright, [2009,Kadirko, [2013].
can be traced back to the work of Dunlap and Kenkre, Dunlap, [1986] where their results concerning dynamic localization are extended to long-range interactions in a 1D lattice with hopping elements An and lattice constant a. The case where all the interactions are considered led to the new concept of exact dynamic localization in the presence of an AC electric field Dignam, [2002]. Such a concept of "band engineering" with long-range interactions has been also investigated (theoretically and experimentally1 in optical lattices; Longhi, [2010,Madison et al., [1998] reported the first observation of dynamical suppression of the band due to an external AC field in an optical lattice whereby the bandwidth shrinks to zero and the Bloch states become localized when the field amplitude meets a condition that was also derived in Mamani et al. Mamani, [2017] using the semiclassical method.2 More recent investigations in layered graphene systems show that the effects derived from an extended tight-binding Hamiltonian can be considered as improvements to the usual nearest neighbor model results Reich, [2002,Kundu, [2011,Wright, [2009,Kadirko, [2013].
In this work we use an extended tight-binding Hamiltonian where the long-range interactions correspond to a bidimensional system, namely, an square lattice; then, we set about establishing a formal equivalence between that lattice and a two-mesh LC circuit with discrete charge by means of deriving and comparing their corresponding effective Hamiltonians (the case of a 1D lattice and its relation to the single-mesh LC circuit with discrete charge has been already studied by Mamani et al. Mamani, [2018]. We show that such an equivalence is possible by managing the parameters of the driving oscillating field (with frequency ω) acting upon the square lattice such that the nearest neighbor interactions become effectively suppressed leaving the remanent next-to-nearest neighbor (2nd neighbor) interactions as the dominant ones at order ω0 plus the 3rd neighbor interactions at order ω-2. The theoretical framework for the study of quantum circuits with discrete charge is referred to Chen and Li, [1996] wherein the fundamental commutator ![]() is defined: nqe are the discrete eigenvalues of the electric charge operator
is defined: nqe are the discrete eigenvalues of the electric charge operator ![]() (n is an integer and qe is the elementary electronic charge), the flux operator
(n is an integer and qe is the elementary electronic charge), the flux operator ![]() is the conjugate of
is the conjugate of ![]() and the substitution
and the substitution ![]() takes into account the discrete nature of the electric charge Flores, [2005,Calcina-Nogales, [2013,Flores, [2002]. The physical phenomena associated to these kind of systems have been reported: persistent currents, Bloch oscillations in quantum circuits, Coulomb blockade, current magnification, voltage and current engineering Chen and Li, [1996,Flores, [2005,Flores, [2002,Chen, [2005,Calcina-Nogales, [2020], etc. These cases demonstrate the feasibility of modeling the physics of mesoscopic devices within the conceptual framework referred to above.
takes into account the discrete nature of the electric charge Flores, [2005,Calcina-Nogales, [2013,Flores, [2002]. The physical phenomena associated to these kind of systems have been reported: persistent currents, Bloch oscillations in quantum circuits, Coulomb blockade, current magnification, voltage and current engineering Chen and Li, [1996,Flores, [2005,Flores, [2002,Chen, [2005,Calcina-Nogales, [2020], etc. These cases demonstrate the feasibility of modeling the physics of mesoscopic devices within the conceptual framework referred to above.
Although the one-dimensional and the square tight-binding lattices do not exist as such (to our knowledge), it seems that the reported discrete-charge mesoscopic systems would be soon technicaly feasible, thus, permitting the posibility of testing the predictions deduced from comparing both systems. In this sense, the semiclassical method together with the time-averaging techniques provide an easier and more straightforward way of deriving an effective Hamiltonian, as we could in fact verify in the derivation of the quantum effective Hamiltonian of the two-mesh LC circuit Calcina-Nogales, [2020]. Besides, the semiclassical method also provides a bifurcation condition already studied in the one-dimensional lattice Mamani, [2018] and suggested in the two-dimensional case (in this work) that could be useful for predicting the transition between different electronic dynamical regimes.
The organization of our work is the following: in Section 2 we derive the effective Hamiltonian for a square lattice using the time-averaging technique and extending the procedures we have already used for the one-dimensional lattice Mamani, [2017]; in Section 3 we apply the results of the previous section to the managing of the effective Hamiltonian hopping elements so as to emulate case of the two-mesh LC circuit with discrete charge; finally, in Section 4 we present the most important concluding remarks and point out some directions for future research.
2. Derivation of the effective Hamiltonian for the square lattice
Consider the extended tight-binding Hamiltonian function with nearest-neighbor and next-to-nearest neighbor interactions for an independent test particle with charge qe (i.e., we do not consider any possible interaction with like particles whatsoever neither the particle affects the distribution of the external electric fields acting upon it) which hops in a square lattice with cells of side a under the action of external electric fields,
![]()
The tight-binding band in the Hamiltonian (1) has the standard form ![]() where k=(kx,ky) and Rm,n=a(m,n); the hopping elements are A = γ0,±1= γ±1,0 for the nearest neighbors and C =
where k=(kx,ky) and Rm,n=a(m,n); the hopping elements are A = γ0,±1= γ±1,0 for the nearest neighbors and C = ![]() for the next-to-nearest neighbors. In the following derivation, and in order to deal with a more compact notation, we take unitary numerical values for the lattice constant a and for the physical constants qe, ħ. V(r) is an external arbitrary static potencial energy at r=(x,y) and f(ωt)=(fx,fy) is the rapidly oscillating external driving field with frequency ω >> 1/T, where T is the particle's characteristic period of oscillation in the absence of the driving field. Without loss of generality and for the sake of simplicity, we will suppose that the external electric field f(ωt) is an even function of t.
for the next-to-nearest neighbors. In the following derivation, and in order to deal with a more compact notation, we take unitary numerical values for the lattice constant a and for the physical constants qe, ħ. V(r) is an external arbitrary static potencial energy at r=(x,y) and f(ωt)=(fx,fy) is the rapidly oscillating external driving field with frequency ω >> 1/T, where T is the particle's characteristic period of oscillation in the absence of the driving field. Without loss of generality and for the sake of simplicity, we will suppose that the external electric field f(ωt) is an even function of t.
Although the quantum Hamiltonian corresponding to with V(r)=0 has the spatial divergent potential r ·f(ωt), the problem of finding its eigenfunctions has been already widely treated in terms of the vector potential representation Houston, [1940,Krieger, [1986,Kittel, [1987,Rossi, [1997] whereby the electric field is f(ωt)= ∂g/∂t, such that the momentum operator is shifted as p → p+ g within the kinetic energy operator. As a consequence, the "acceleration theorem" ∂k/∂t=f(ωt) is derived strictly quantum-mechanically in agreement with the semiclassical approach considered in our work.3 For the case of V(r) ≠ 0 in , the gauge substitution g → g+ ∇V(r)t is made and the resulting acceleration theorem becomes ∂k/∂t=f(ωt)-∇V(r).
We use now the Hamilton's equations which yield the time derivatives of the position and the momentum:
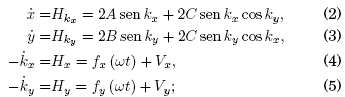
we set the notation Vx, Vy, Vxx, Vyy, Vxy=Vyx and Hkx, Hky, Hx, Hy for the derivatives of V(r) and H(r,k;t) respectively; this notation will apply only to the Hamiltonian and potential energy functions hereafter. It will be convenient also to use the generic symbol z for either of the coordinates x,y where a simplified expression could be written. Let us now apply the canonical transformations between the momenta: (z,kz)→(z,k’z) given by k’z ≡ kz+gz, whereby the "displaced momentum" k’z is defined along with the time integral of the external field, ![]() ; this is the realization of the vector potential representation that yielded k → k+ g as projected onto the square lattice and which was already referred to. The substitution of these transformations in (2)-(5) yields:
; this is the realization of the vector potential representation that yielded k → k+ g as projected onto the square lattice and which was already referred to. The substitution of these transformations in (2)-(5) yields:
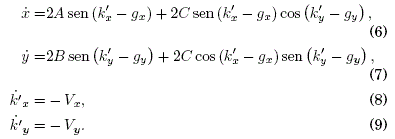
Due to the action of the combined static and oscillating fields, -∇V(x,y) and f(ωt), the particle will move with small oscillations around a slow varying trajectory. Thus, we introduce the "slow" Z(t), Kz(t) coordinates and the "fast" ξz(τ), ηz(τ) coordinates in the direct and reciprocal spaces respectively; the fast coordinates are considered perturbations of the slow coordinates:
![]()
where τ ≡ ωt is such that the time-average of ξz(τ), ηz(τ), vanish in the time interval with period T=2π/ω while Z(t), Kz(t), remain almost constant in the same interval, i.e., ⟨ ξz ⟩ = ⟨ ηz ⟩ =0, and ⟨ Z ⟩ =Z(t), ⟨ Kz ⟩ =Kz(t). We have used the definition of the time-average as ![]()
The set of transformations
![]()
is canonical since the structure of Hamilton's equations is preserved Landau, [1985]:
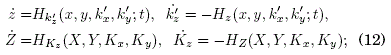
this is so as a consequence of the invariance of the Poisson brackets: [kz,z]=[k’z,z]=[Kz,Z]=1 which yields H(x,y,k’x,k’y;t)=H(x,y,kx,ky;t)+∂F(x,y,k’x,k’y;t)/∂t for some generating function F(x,y,k’x,k’y;t) that can be readily calculated, and the time-averaging which gets us from H(x,y,k’x,k’y;t) to H(X,Y,Kx,Ky). The resulting shift of the time dependence from the r ·f(τ) term in H(x,y,kx,ky;t) into the arguments of the kinetic energy operators in H(x,y,k’x,k’y;t) is not only a convenient transformation (in order to get time-averages efficiently) but it is also a necessary one to render k=(kx,ky) as a "good quantum number" Kittel, [1987]. Now, H(X,Y,Kx,Ky) ≡ Heff is the form of the effective Hamiltonian that, as a result of the Hamilton's equations, represents a constant of motion and whose explicit construction will be possible giving the resulting Eq.(7) at the end of this section. In this work we will restrict the potential energy to the quadratic form of the position coordinates V(x,y)=c1 x2+c2 y2+c3 xy since it is this kind of function that yields the correct physical interpretation for Heff as a tight-binding Hamiltonian (the physical realization of such V(x,y) onto the square lattice plane would be achieved -in principle- by placing the plane inside a dielectric cylinder shell with an specific surface charge distribution); otherwise, if V(x,y) had the form of a higher degree polynomial function, Heff could still be a valid Hamiltonian but not with the form of a tight-binding one Mamani, [2017].
By replacing the time-derivatives of the terms in (12) into the system (6)-(9) we obtain the system (B1)-(B4) in Appendix B wherein we applied the time-average techniques that yield the system for the effective dynamical coordinates:
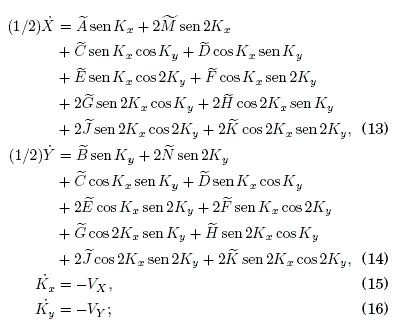
the list of the "tilde" symbols used in (13) and (14) is defined in the Appendix A. We now set up about constructing the effective Hamiltonian Heff ≡ H(X,Y,Kx,Ky) from the system -. The Hamilton equations in the space of the effective coordinates Z, Kz must be satisfied:
![]()
the expression for ![]() in (17) is substituted from (13), (14) and combined together with (15), (16) to give
in (17) is substituted from (13), (14) and combined together with (15), (16) to give
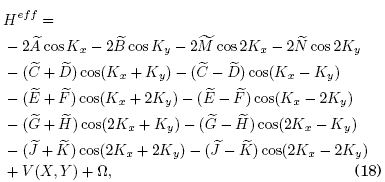
where Ω is a constant term independent of the dynamical coordinates Z, Kz. It is now clear that the "tilde" symbols referred to in (13) and (14) constitute the effective hopping elements characteristic of the effective tight-binding Hamiltonian Heff in (18).
As a first crosscheck calculation of (18) we can test it for the case of the null electric field f=0 and a linear static potential V(X,Y)=αX+βY (dropping the constant term Ω):
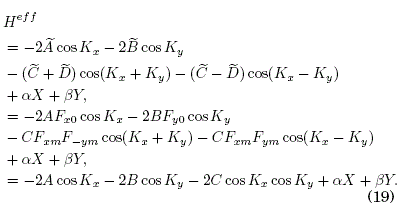
By using Hamilton's equations ![]() in (17) for Z=X,Y, we obtain
in (17) for Z=X,Y, we obtain
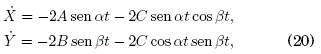
which describe, as expected, a 2D Bloch oscillation with period T=2pπ/α (p=min(n,m)) for the rational quotient α/β = n/m.
3. Interactions engineering and relation to an LC circuit
With the explicit form of the effective Hamiltonian Heff in (18) in terms of the Fourier components fzn of the electric field via (B31), we may ask now which components will yield specific values of the effective hopping elements in Heff that determine thus the transport properties of the particle in a square lattice when acted upon by the external fields. This is the "interactions engineering" scheme considered in this paper, particularly, as an extension of the one-dimensional case investigated by Mamani et al. Mamani, [2017]. For the purpose of illustrating such interactions engineering, we choose as a case study the emulation of an LC circuit with discrete charge that has an effective Hamiltonian of the form (as we will see later in this section)
![]()
where the static potential is the quadratic form V(X,Y) ∞ X2+Y2+(X-Y)2 such that its second derivatives are VXX=VYY=-2 VXY. In this case, and for the square lattice with A=B, the effective hopping elements become (Appendix A):
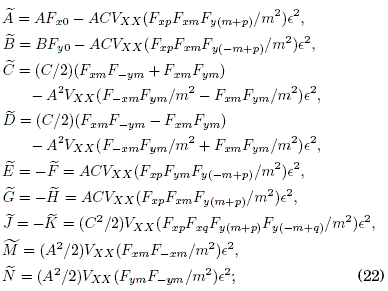
sums are performed on the terms with the repeated indices m, p, q and the variable m. Since our perturbative calculations were performed consistently up to second order in ∈ ≡ 1/ω, the effective hopping elements in (22) can be expressed as combinations of the zeroth (dominant) and 2nd order terms: ![]()
![]()
![]() .
.
Now, the Fzm terms in (22) depend on the specific oscillating electric field f=(fx,fy) through its Fourier components. For the purpose sought in this work, we find that those components should be
![]()
Then, the expression for Fzm in (B31) readily becomes
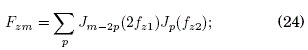
notice the property F(-z)m= Fz(-m) ≡ F-zm. In order to solve the infinite sum in (24) and verify its convergence, we use the integral representation for Jn(z):
![]()
Replacing this Jn(z) in Fzm and using ![]() we obtain
we obtain
![]()
Now, we set fx2= fy1= 0 in (23) as the condition to find the required form of HLC (![]() in this case) with the parameters fx1, fy2 such that:
in this case) with the parameters fx1, fy2 such that:
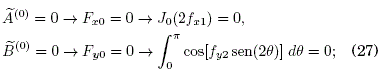
then, we chose from the set of solutions {fx1,fy2} of those which satisfy the condition that ![]() should be negligible as compared to
should be negligible as compared to ![]() and
and ![]() . One way of doing this is to calculate the euclidian norm
. One way of doing this is to calculate the euclidian norm
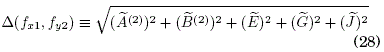
such that ![]() attains a minimum value for negative values of
attains a minimum value for negative values of ![]() Thus, with this condition and those of (27) fulfilled, the effective Hamiltonian in (18) becomes
Thus, with this condition and those of (27) fulfilled, the effective Hamiltonian in (18) becomes
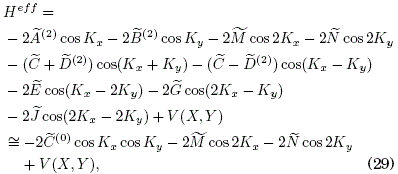
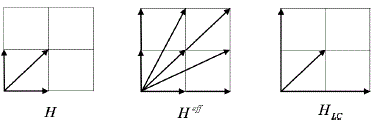
thus attaining the required approximation ![]() . Fig. 1 shows an schematic representation of the interactions in the square lattice (from left to right): the time-dependent Hamiltonian H in (1) is transformed into the effective Hamiltonian in Heff (18) (with all the reparametrized and induced interactions) by the action of the external oscillating and static fields and, finaly, by choosing specific values of the those fields ("interactions engineering"), the Hamiltonian HLC in (29) is obtained.
. Fig. 1 shows an schematic representation of the interactions in the square lattice (from left to right): the time-dependent Hamiltonian H in (1) is transformed into the effective Hamiltonian in Heff (18) (with all the reparametrized and induced interactions) by the action of the external oscillating and static fields and, finaly, by choosing specific values of the those fields ("interactions engineering"), the Hamiltonian HLC in (29) is obtained.
Figure 1: Representations of the interactions in the square lattice (from left to right): the time-dependent
Hamiltonian H in , the effective Hamiltonian Heff in , the Hamiltonian HLC in obtained by choosing specific
values of the external fields (interactions engineering).
The numerical results found from (27) and (28) within the interval 0 < fx1,fy2 < 100 (with physical units restored) are
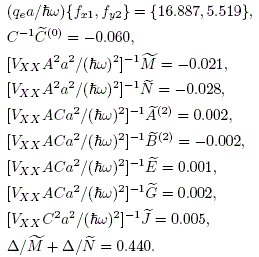
We expect that VXX A2a2/(ħ ω)2 has an upper bound in order to have consistent results, i.e., ![]() dominant with respect to
dominant with respect to ![]() and
and ![]() . This is of course the case when
. This is of course the case when ![]() but, as we will see at the end of this section, ω must also have an upper bound if an analogy between the square lattice and the LC circuit is to be achieved. We think that values of the physical parameters can be found that meet reasonably such a requirement.
but, as we will see at the end of this section, ω must also have an upper bound if an analogy between the square lattice and the LC circuit is to be achieved. We think that values of the physical parameters can be found that meet reasonably such a requirement.
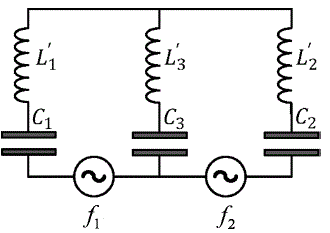
Figure 2: Two-mesh LC circuit.
We now set up about describing the LC circuit depicted in Fig. 2. Following the construction of the quantum Hamiltonian operator for a two-ring system Flores, [2002], we can construct the Hamiltonian function of a two-mesh LC circuit with discrete charge qe as
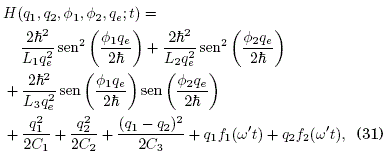
which follows from the replacement of the magnetic flux as ![]() in the corresponding continuous-charge Hamiltonian function
in the corresponding continuous-charge Hamiltonian function
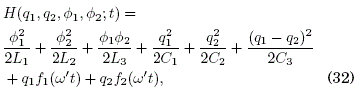
where we have defined: 1/L1 ≡ (L2’+L3’)/Υ, 1/L2 ≡ (L1’+L3’)/Υ and 1/L3 ≡ 2 L3’/Υ, with Υ ≡ (1/2)∑i ≠ j Li’Lj’; as can be readily checked the flux φi remains invariant in the limit qe → 0 yielding, as required, H(q1,q2,φ1,φ2,qe;t) → H(q1,q2,φ1,φ2;t). In this case, the term φ1 φ2/(2 L3) in (32) is derived from the energy term (1/2)L’3(·q1-·q2)2 according to the Kirchhoff's laws. The mutual inductance terms corresponding to this circuit are φ1 φ2/M12, φ1 φ3/M13 and φ2 φ3/M23 but we have not considered them in (32) since we did not specify the form of the couplings among L’1, L’2 and L’3. In fact, the "mesoscopic" character of this circuit lies upon the discrete nature and small quantity (about 10) of the elementary electric charges being allocated in the capacitors and not necessarily upon the small size of the circuit which would imply couplings among the inductors.4
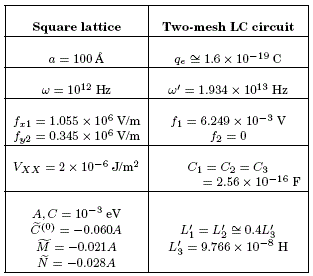
Table 1: Numerical values of the physical parameters. The values of a, ω, A, C were chosen so as to
resemble typical values in a GaAs-type semiconductor superlattice; f2=0 was suggested so as to
facilitate the calculations. The other values result from comparing the terms and arguments of the
effective Hamiltonians and , and from the corresponding algebraic and numerical manipulations.
Following the standard quantum time-average techniques Rahav, [2003,Calcina-Nogales, [2020] and setting the canonical transformations φ1=Φ1+πħ/qe and φ2=Φ2+πħ/qe, we obtain from (32) the effective Hamiltonian function5
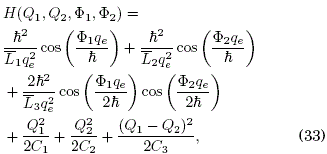
where, for the case of the AC source voltages f1(ω’t)=2 f1 cos(ω’t) and f2(ω’t)=2 f2 cos(2 ω’t), we obtain
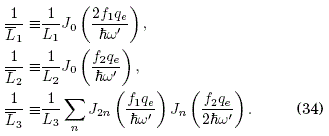
By comparing the terms and arguments of H(Q1,Q2,Φ1,Φ2) in with those of HLC(X,Y,Kx,Ky) in we can verify, as expected, that the required form of HLC is attained for static potential energies V(Q1,Q2) and V(X,Y) whose second derivatives are related as VQ1 Q1/VXX=VQ2 Q2/VYY=VQ1 Q2/VXY=(a/qe)2 . Specifically, by choosing equal capacitances in , we should have that VXX=2(qe/a)2/C1.
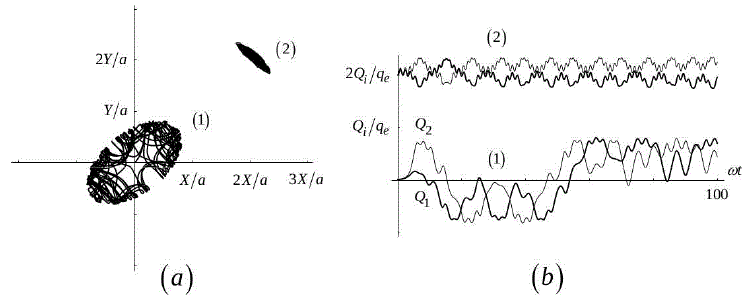
Figure 3: Cases of electronic motion in: (a) the effective position XY plane, and (b) the two-mesh LC circuit. In case
(a) the displacements are measured in units of the lattice constant a=100 A; in case (b) the capacitors' electric charges are
measured in units of the electron's charge qe, the time is measured in units of the frequency inverse 1/ω = 10-12 s.
Cases (1) and (2) in both (a) and (b) correspond to oscillations with zero and positive time-averages, respectively. Cases (1)
and (2) in (b) resemble very much the AC and DC regimes, respectively, deduced in the one-mesh LC circuit Mamani, [2018]
as a consequence of a bifurcation condition.
From the numerical values of fx1, fy2, ![]() ,
, ![]() and
and ![]() found in , we may now express the equivalence among the coefficients of H(Q1,Q2,Φ1,Φ2) and HLC(X,Y,Kx,Ky) in the compact notation that comprises the three equations
found in , we may now express the equivalence among the coefficients of H(Q1,Q2,Φ1,Φ2) and HLC(X,Y,Kx,Ky) in the compact notation that comprises the three equations
![]()
whence the the source voltage amplitudes f1, f2 and the inductances can be found. We may take L’1=L’2 for simplicity, thus, from ![]() in , we have that
in , we have that ![]() which is satisfied for an infinte set of solutions, for example, (qe/ħω’) f1=0.517 and (qe/ħω’) f2=0 (although f2=0 was so chosen just to facilitate the calculations, such a value still deserves a further phyisical interpretation). For these values, and by setting
which is satisfied for an infinte set of solutions, for example, (qe/ħω’) f1=0.517 and (qe/ħω’) f2=0 (although f2=0 was so chosen just to facilitate the calculations, such a value still deserves a further phyisical interpretation). For these values, and by setting ![]() ,
, ![]() in the Hamiltonians (21), (33), respetively, we find
in the Hamiltonians (21), (33), respetively, we find
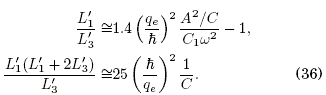
As we can see, the term (qe/ħ)2 (A2/C)/(C1 ω2) has to have a lower bound to yield positive inductances; such a bound will be determined by the characteristics of the square lattice which, in this work, can be thought of as a 2D semiconductor superlattice of the GaAs type (and whose 1D version was where Bloch oscillations were first observed). Thus, we may take as typical values:
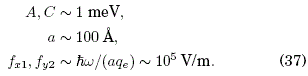
From the latter we have an estimation of ω ![]() 1012 Hz. Since VXX (Aa/ħ ω)2=(A qe/ħ)2/(C1 ω2)
1012 Hz. Since VXX (Aa/ħ ω)2=(A qe/ħ)2/(C1 ω2) ![]() 10-22 J should hold in (30), we have then the estimation of C1
10-22 J should hold in (30), we have then the estimation of C1![]() 10-16 F. With these values, we have therefore from (36) that
10-16 F. With these values, we have therefore from (36) that ![]() H. Finally, an estimation of the sources frequency ω’ can be made by assuming that a maximum of just few electrons is to be alloted in a (small) mesoscopic capacitor, which is other way for interpreting the meaning of "discrete charge" LC circuit. We may take then Q1,max=10 qe, which, together with
H. Finally, an estimation of the sources frequency ω’ can be made by assuming that a maximum of just few electrons is to be alloted in a (small) mesoscopic capacitor, which is other way for interpreting the meaning of "discrete charge" LC circuit. We may take then Q1,max=10 qe, which, together with ![]() V and ω’
V and ω’ ![]() 1013 Hz. More precise values for the results of our numerical simulations and from comparing the terms and arguments of the effective Hamiltonians (33) and (21) are summarized in Table 1 .
1013 Hz. More precise values for the results of our numerical simulations and from comparing the terms and arguments of the effective Hamiltonians (33) and (21) are summarized in Table 1 .
We may now validate the consistency of the semiclassical model invoked in our work: the value of the frequency ω = 1012 Hz corresponds to an external field wavelength λ ![]() 10-3 m, while the lattice constant is a=100 A. The quantum wavepacket size can be taken from Mamani et al. Mamani, [2017], where the semiclassical method has proved to be consistent with the formal quantum approach for a wavepacket initial width Δx=10 a. We have therefore that λ >> Δx >> a, as required for the validity of the semiclassical method (see, for example Ashcroft and Mermin, [1976]), and which in turn implies that the intensity of the external electric field |f|
10-3 m, while the lattice constant is a=100 A. The quantum wavepacket size can be taken from Mamani et al. Mamani, [2017], where the semiclassical method has proved to be consistent with the formal quantum approach for a wavepacket initial width Δx=10 a. We have therefore that λ >> Δx >> a, as required for the validity of the semiclassical method (see, for example Ashcroft and Mermin, [1976]), and which in turn implies that the intensity of the external electric field |f| ![]() 106 V/m is low enough for a single-band tight-binding model Hamiltonian to hold.
106 V/m is low enough for a single-band tight-binding model Hamiltonian to hold.
By solving numerically the system of equations (17) for X(t), Y(t), Q1(t), Q2(t), with the values reported in Table 1, we may relate the electronic dynamics in both equivalent systems, the square lattice and the two-mesh LC circuit. Since we have managed the electric fields and the voltage sources in the former and latter systems, respectively, so as to have HLC(X,Y,Kx,Ky) ≅ HLC(Q1,Q2,Φ1,Φ2), then their common energies are 0.218 meV, corresponding to the initial values X(0)=Y(0)=0.02 a of the effective position coordinates. We observe in Fig. 3(a(1)) a predominately diagonal oscillating motion -although not a simple one- of the particle's position about the origin of the effective position XY plane of the square lattice, which corresponds also to a predominately symmetric distribution of oscillating charges in the two-mesh LC circuit, as seen in Fig. 3(b(1)), in accordance with the diagram for HLC in Fig. 1, where the diagonal hopping element is the dominant one. Such a behavior, however, may change abruptly -as a function of the total energy, for example- giving rise to a DC regime or a supression of the mesh currents, as it does in the one-dimensional case of the one-mesh LC circuit Mamani, [2018], where we have showed that a bifurcation condition on the · Q-Q phase diagram can be associated to such an abrupt change. Figs. 3(a(2)) and 3(b(2)) show position and charge oscillations with positive time-averages corresponding to an energy of 2.707 meV, contrasting with those of Figs. 3(a(1)) and 3(b(1)). The extension of the one-dimensional bifurcation condition to the two-dimensional case of the two-mesh circuit and its relation to the particle's propagation in the square lattice is an interesting issue worth to be treated elsewhere.
4. Conclusions
We have established the formal equivalence between two physical systems by means of the interactions engineering scheme developed in this paper. Those systems are: (i) a square lattice wherein an tight-binding electron propagates under the combined action of an external high-frequency and homogeneous electric field and a quadratic static potential, and (ii) a two-mesh LC circuit with discrete charge. Such formal equivalence is attained by describing both systems by effective Hamiltonian functions having the same form and whose parameters can be numerically calculated when the Hamiltonian terms are correspondingly compared among them; for deriving such effective Hamiltonians we have used perturbative expansions up to ω-2 when ![]() . Interestingly, we have found that the sought equivalence between the square lattice and the LC circuit is achieved when we choose specific values of the oscillating electric field acting upon the lattice so that the 1st neighbor interactions (
. Interestingly, we have found that the sought equivalence between the square lattice and the LC circuit is achieved when we choose specific values of the oscillating electric field acting upon the lattice so that the 1st neighbor interactions (![]() ) are suppressed and the remaining 2nd neighbor interactions (
) are suppressed and the remaining 2nd neighbor interactions (![]() ) and 3rd neighbor interactions (
) and 3rd neighbor interactions (![]() ,
,![]() , order ω-2) become comparable (see Table 1).
, order ω-2) become comparable (see Table 1).
We now suggest some interesting issues that could be worth exploring further: (a) In a previous work we have investigated the relation between a single-mesh LC circuit (with discrete charge) and a charged particle hopping in a one-dimensional lattice Mamani, [2018]; in the present work we have extended such an analogy to a two-mesh LC circuit and a square lattice. Thus, it seems natural to inquire whether the extension to a three-mesh LC circuit and a cubic lattice would be valid, mainly, because the one-dimensional and the square lattices do not exist as such (to our knowledge), but the three dimensional cubic lattice does exist (although not with the superlattice parameters specified in Table 1). (b) Another natural extension of our work would be considering a rectangular lattice where, for example, the sides have an incommensurate ratio of ![]() In fact, this latter case would be the best suited for simulating the dynamics of a hopping electron in graphene. (c) Finally, and motivated by the results in Fig. 3(a) for the square lattice, we may suggest that the "AC regime" would indicate a quantum regime where the electronic probability densities corresponding to neighbor lattice sites overlap, which indicates in turn a higher electric conductivity, as compared to the "DC regime". Thus, a higher and a lower conducting regimes could be separated by a semiclassical bifurcation condition.
In fact, this latter case would be the best suited for simulating the dynamics of a hopping electron in graphene. (c) Finally, and motivated by the results in Fig. 3(a) for the square lattice, we may suggest that the "AC regime" would indicate a quantum regime where the electronic probability densities corresponding to neighbor lattice sites overlap, which indicates in turn a higher electric conductivity, as compared to the "DC regime". Thus, a higher and a lower conducting regimes could be separated by a semiclassical bifurcation condition.
Footnotes:
1Many of the current theoretical models do not take into account some real physical effects (for simplicity), such as interband transitions, dispersion of the hopping particle by thermal collisions and phononic interactions, loss of crystal periodicity, etc., due which the particle's wavepacket usually decoheres rapidly and the observation -for example- of Bloch oscillations is restricted to a few complete periods (c.f.: Lyssenko et al., [1997,Madison et al., [1998]). In the absence of such effects, the wavepacket's width may oscillate and eventually be restored to its initial value, as shown, e. g., by Dignam and de Sterke in the exact dynamic localization effect Dignam, [2002].
2A concise and pedagogical justification of the semiclassical method for a general periodic potential can be found, for example, in Ch. 12 of Ashcroft and Mermin, [1976]
3In this sense, the semiclassical method provides exact results that coincide with the quantum ones, as we could verify in the above mentioned references and also in Dignam and de Sterke,Dignam, [2002] wherein a study of exact dynamical localization is carried on (we have work in progress in this direction).
4Interestingly, the phenomenon of current magnification referred to by Flores and Utreras Flores, [2002] for two coupled inductances would also occur in the two-mesh circuit with three inductances studied in our work; progress is being carried on by us in that direction.
5The resulting Hamiltonian operator corresponds to the Hamiltonian function obtained with the semiclassical scheme, as was already done in the case of the single-mesh LC circuit Mamani, [2018].
References
Ashcroft N. & Mermin N. D. 1976, Solid State Physics (Saunders College, Philadelphia). [ Links ]
Bandyopadhyay M. & Dattagupta S. 2008, Pramana J. Phys. 70, 381. [ Links ]
Calcina-Nogales M. 2003, Mod. Phys. Lett. B 27, 1350138. [ Links ]
Calcina-Nogales M., Mamani E. & Sanjinés D. 2020, preprint. [ Links ]
Chen B. & Li Y. Q 1996, Phys. Rev. B 53, 4027. [ Links ]
Chen B. 2005, Phys. Lett. A 335, 103. [ Links ]
Dignam M. M. & de Sterke C. M. 2002, Phys. Rev. Lett. 88, 4, 046806. [ Links ]
Dunlap D. H. & Kenkre V. M. 1986, Phys. Rev. B 34, 3625-3633. [ Links ]
Flores J. C. & Utreras-Díaz C. A. 2002, Phys. Rev. B 66, 153410. [ Links ]
Flores J. C. & Lazo E. 2005, IEEE 4, 688. [ Links ]
Houston W. V. 1940, Phys. Rev. 57, 184. [ Links ]
Itin A. P. & Neishtadt A. 2014, Phys. Lett. A 378, 822. [ Links ]
Itin A. P. & Katsnelson M. I. 2015, Phys. Rev. Lett. 115, 075301. [ Links ]
Kadirko V., Ziegler K. & Kogan E. 2013, Graphene 2, 97. [ Links ]
Kapitza P. L. 1965, in Collected Papers of P. L. Kapitza, edited by ter Haar D. (Pergamon Press, Oxford); Kapitza P. L. 1951, Zh. Eksp. Teor. Fiz. 21, 588. [ Links ]
Kittel C. 1987, Quantum Theory of Solids (John Wiley and Sons, New York). [ Links ]
Krieger J. B. & Iafrate G. J. 1986, Phys. Rev. B 33, 5494. [ Links ]
Kundu R. 2011, Mod. Phys. Lett. B 25, 163. [ Links ]
Landau L. D. & Lifschitz E. M. 1985, Mecánica (Reverté, Barcelona). [ Links ]
Longhi S., Dreisow F., Heinrich M., Pertsch T., Tünnermann A., Nolte S. & Szameit A. 2010, Phys. Rev. A 82, 053813. [ Links ]
Lyssenko V., Valusis G. & Löser F. 1997, Phys. Rev. Lett. 79, 301. [ Links ]
Madison K. W., Fischer M. C., Diener R. B., Niu Q. & Raizen M. G. 1998, Phys. Rev. Lett. 81, 23, 5093. [ Links ]
Mamani E., Calcina-Nogales M. & Sanjinés D. 2017, Int. J. Mod. Phys. B 31, 1750116. [ Links ]
Mamani E., Calcina-Nogales M. & Sanjinés D. 2018, Rev. Mex. Fis. 64, 456-463. [ Links ]
Rahav S., Gilary I. & Fishman S. 2003, Phys. Rev. A 68, 013820. [ Links ]
Reich S., Maultzsch J., Thomsen C. & Ordejón P. 2002, Phys. Rev. B 66, 035412. [ Links ]
Rossi F. 1997, Bloch oscillations and Wannier-Stark localization in semiconductor superlattices (Theory of transport properties of semiconductor nanostructures, ed. E. Schoell, Chapman and Hall, London). [ Links ]
Wright A. R., Liu F. & Zhang C. 2009, Nanotechnology 20, No. 40. [ Links ]
Appendix
A Definitions of the effective hopping elements
The "tilde" symbols used in (13) and (14) that constitute the effective hopping elements of Heff in (18) are defined as:
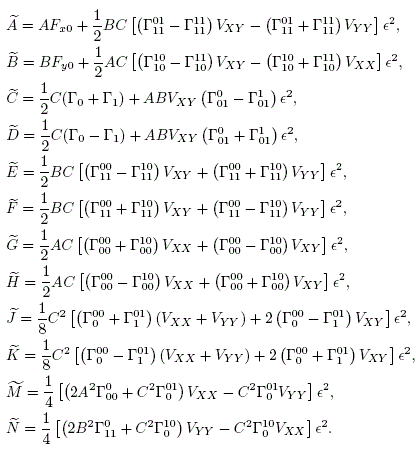
The definitions of the "Γ" symbols used above are:
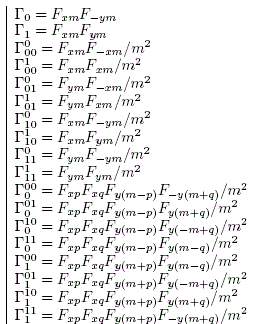
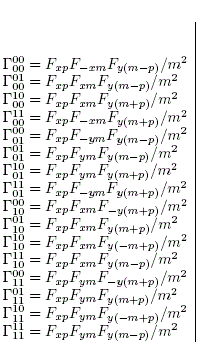
Sums are performed on the terms with the repeated indices m, p, q and the variable m.
B Time-average derivation of the effective dynamical coordinates
In this Appendix we apply the time-average techniques that yield the system for the effective dynamical coordinates (13)-(16). This is done by replacing the time-derivatives of the terms in (10) into the system (6)-(9) yielding:
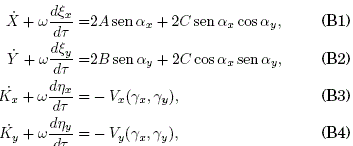
where we have defined αz ≡ Kz+ηz-gz, γz ≡ Z+ξz. We will use later αz0 ≡ Kz+ηz0-gz which results from evaluating αz for ∈ = 0, and αz00 ≡ Kz-gz which results from evaluating αz0 for ηz0=0. The application of the time-average properties to the system (B1)-(B4) yields:
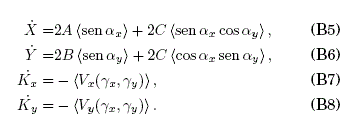
Combining (B5)-(B8) and (B1)-(B4) one obtains a system for the fast coordinates:
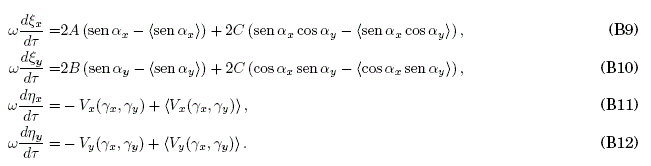
The solutions of (B9)-(B12) are to be substituted in (B5)-(B8) in order to have a system of differential equations for the slow coordinates Z, Kz. To achieve that, and since the frequency ω is large, we expand the fast coordinates ξz, ηz as power series of the small parameter ∈ ≡ t/τ = 1/ω up to the order of ∈2 with coeficients ξzi, ηzi. The substitution of these series in two of the trigonometric functions and in the derivatives Vx, Vy in (B5)-(B8) leads to
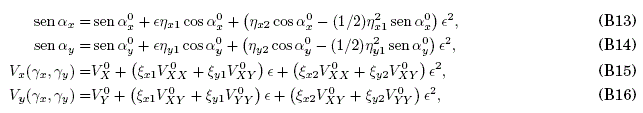
where γz0 ≡ Z+ξz0; the superscript "0" in the derivatives of the potential energy means that its argument is γz0 and the abscence of a superscript means that the argument is Z. Substituting (B13)-(B16) in (B9)-(B12), and comparing the terms in the same powers of ∈, one obtains:
(i) For ∈0,
![]()
(ii) For ∈1,
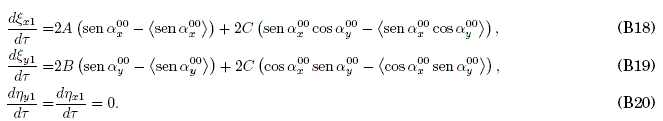
(iii) For ∈2,
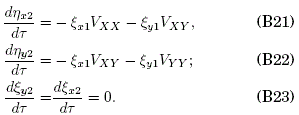
The convenient solutions for (B17), (B20) and (B23) are chosen as ξx0=ηx0=ξy0=ηy0=0, ηz1=0 and ξz2=0, respectively. The resulting right-hand side of the system (B5)-(B8) stands now as:
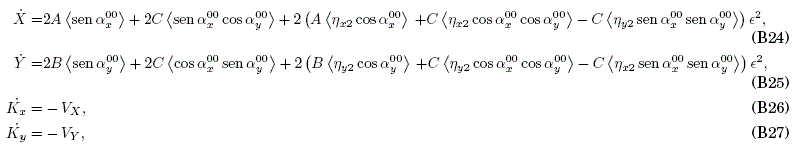
where αz00 depends on Kz and on the external fields, while ηz2 is to be found by solving (B18), (B19), (B21) and (B22). The result will be the sought system of differential equations for the slow coordinates Z, Kz whose solution will permit us to deduce the effective Hamiltonian function H(X,Y,Kx,Ky).
Let us express the trigonometric functions in (B24), (B25) in complex form:
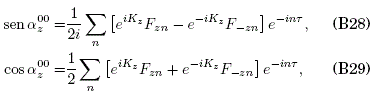
where we have used the following Fourier expansion given that gz(τ) is a periodic real and odd function of t, corresponding to the real and even function fz(τ):
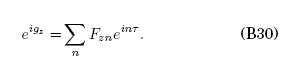
For the external field ![]() the coefficients Fzn are
the coefficients Fzn are
![]()
Substituting now (B28), (B29) in (B18), (B19), and solving these along with (B21), (B22) for ηz2 we find:
![]()
where
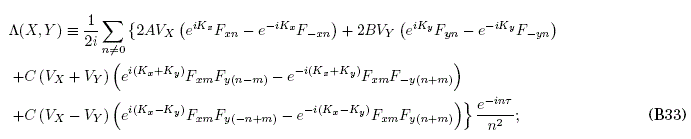
a sum in Λ is performed on the terms with the repeated index m. Substituting now (B32), (B28) and (B29) in (B24) and (B25), and performing the time-average operations with ![]() , we obtain the system for the effective dynamical coordinates X, Y, Kx, Ky given in (B13)-(B16)
, we obtain the system for the effective dynamical coordinates X, Y, Kx, Ky given in (B13)-(B16)