Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.36 n.36 La Paz nov. 2020
A. ARTICLES
Condiciones extendidas de sincronización de dos mapas logísticos acoplados
Synchronization extended conditions of two coupled logistic maps
R. O. E. Bustos Espinoza, G. M. Ramírez Ávila
http://www.fiumsa.edu.bo/docentes/rbustos/
http://www.fiumsa.edu.bo/docentes/mramirez/
Instituto de Investigaciones Físicas, Universidad Mayor de San Andrés, Campus Universitario, c. 27 Cota-Cota, Casilla de Correos 8635, La Paz - Bolivia
(Recibido 10 de agosto de 2020; aceptado 15 de septiembre de 2020)
Resumen
Se analizan las regiones de sincronización de dos mapas logísticos acoplados difusivamente en un amplio plano de parámetros. Se encontraron nuevas estructuras bien definidas que amplifican la caracterización de dos osciladores móviles. Debido a su simplicidad y a su rico comportamiento dinámico, los mapas logísticos acoplados nos permiten estudiar diferentes tipos de sincronización. Nos enfocamos específicamente en la sincronización en fase caracterizándola mediante periodicidades que se presentan simétricamente en el plano de parámetros. Lo anterior, nos permite distinguir claramente entre regiones con comportamiento regular o caótico. finalmente, se indican posibles aplicaciones de este tipo de sistemas.
Código(s) PACS: 05.45.Xt, 05.45.Pq,05.45.-a
Descriptores: Sincronización, caos - sistemas caóticos - dinámica no lineal.
Abstract
We analyze the synchronization regions of two difusively coupled logistic maps in an ample parameter plane where we found new and well-defined structures of synchrony that allow us to amplify the characterization of two motile oscillators. Due to their simplicity and rich dynamical behavior, the coupled logistic maps enable us to study dierent kinds of synchronization. We focus specifically on phase synchronization characterizing it by periodicities that symmetrically pervades the parameter plane. A clear distinction is ound between the above mentioned synchronous regions from those exhibiting chaotic behavior. finally, we point out some possible applications of this kind of system.
Subject headings: Synchronization, chaos - chaotic systems - nonlinear dynamics.
1 Introduction
The synchronization phenomena, so abundant in nature, and extensively studied in a wide variety of systems, from physics to social sciences, is defined by [232001Pikovsky et al.Pikovsky, Rosenblum, & Kurths] as an adjustment of rhythms o sel-sustained oscillators due to their interactions. Several works have been devoted to study synchronous behavior in dierent kind of oscillators, or instance, in electronically-implemented systems, such as the paradigmatic chaotic circuit proposed by Chua and introduced by [211984Matsumoto]. Coupled Chua's circuits give rise to chaotic synchronization firstly formulated intuitively by [301983Tang et al.Tang, Mees, & Chua], and demonstrated aterwards by [71993Chua]. Other interesting circuits exhibiting synchronization are the light controlled oscillators introduced by [242003Ramírez-Ávila et al.], and characterized by their pulsatile coupling; and also that conceived by [152016L'Her et al.L'Her, Amil, Rubido, & Martí] or studying coupled logistic maps. It is worthy to mention the oscillators introduced by [121987Kuramoto & NishikawaKuramoto, & Nishikawa] which became an example or excellence or studying synchronization in dierent network conFigurations in many contexts, including power-grids described by [272014Schultz et al.Schultz, Heitzig, & Kurths], and in mobile agents studied by [92011ujiwara et al.ujiwara, Kurths, & Díaz-Guilera]. The omnipresence of synchronization in nature makes that this phenomenon acquires an essential role in science due to their universal feature that is understood within the nonlinear dynamics conceptual framework as expounded by [81983Fujisaka & Yamada]. The study of synchronization using maps was started with the work of [321983Yamada & Fujisaka]. Some other interesting systems described by maps exhibit synchronization such as in neurons described by [292016Sun & CaoSun, & Cao], [52017Calderón de la Barca, & Ramírez-Ávila] and [102019Iglesias & Ramírez-Ávila], and even in social systems which are studied through the relationship between synchronization and consensus as stated in the edited book of [132013KocarevKocarev], and analyzed in terms of discrete models by [282017Subieta-ríos & Ramírez-Ávila]. Transients or synchronization time, plays also an important role in the description of synchronization as pointed out by [252006Ramírez-Ávila et al.Ramírez, Guisset, & Deneubourg], where they study synchronization regions and transients in locally coupled oscillators in linear and ring conFigurations.
In this work, we describe a huge region o the parameter plane of a systems composed of two coupled logistic maps, where the dynamical behavior allowed us to describe the synchronous behavior of the system according to the coupling strength, and the diference between the oscillators. The description in terms of periodicities gives an insight of the dynamical behavior of such a system. This paper is organized as follows: the logistic map and its features are set forth in Sect. 2, the model or two coupled maps is presented in Sect. 3, where we focus on the types of coupling, the definition o the synchronizability actor, the synchonization regions and some other important remarks. The results are presented in Sect. 4 emphasizing in the aspects related to periodicities and the possibility of varying coupling in relationship with mobile oscillators. finally, in Sect. 5, we give conclusions and some perspectives.
2 The logistic map and its features
The logistic map is represented by a recurrent equation based on a model proposed by [311838Verhulst]. This model describes population dynamics taking into account aspects like birth and death rate.
This map was formulated by [221976May] who realized about the complicated dynamics exhibited by this very simple system including chaotic behavior.
This map has been used in many dierent disciplines and situations going from studies on competitive models, developed by [22001Burgoa & Nogales] to the emergence of coherent motion as studied by [142011Garcóa-Cantú et al.Garcóa-Cantú, Antonopoulos, & Basios], and the spatiotemporal intermittency in coupled maps lattices described by [111985KanekoKaneko], and [61988Chaté & Manneville]. On the other hand, due to their simplicity and robustness as chaos generator, coupled logistic maps have been extensively used to describe synchronization in dierent scenarios as or instance with delayed coupling as studied by [192001Masoller et al.Masoller, Cavalcante, & Rios Leite]. or the above-mentioned reasons, we chose as a model or the dynamics of each of the oscillators a logistic map given by:
Dn+1 = μDn (1−Dn) , (1)
where Dn is a number between zero and one that represents the dynamics of the oscillator. D0 represents the initial condition; μ is the control parameter, a positive number whose value determines the dynamical behavior of the map, and n plays the role of time, as explained in [42012Bustos-Espinoza & Ramírez-Ávila].
2.1 Main hypothesis
We work with two coupled oscillators, considering the following simplifing assumptions concerning their dynamics:
-
The coupled oscillators constitute an isolated system.
-
Each oscillator follows a logistic map dynamics.
-
The oscillators cannot collide.
-
We assume that the oscillators interact in two modes: maintaining a fixed distance between them or not (see Sect. 3)
3 Model
Intending to study the synchronization of two motile or static oscillators, we consider the instantaneous coupling between two logistic maps whose dynamical equations are:
D(1)n+1=μ(1) D(1)n(1−D(1)n)+β12(D(2)n−D(1)n),
D(2)n+1=μ(2) D(2)n(1−D(2)n)+β21(D(1)n−D(2)n) ,(2)
where superscripts identify the oscillators and subscripts represent the temporal evolution, and β represents the coupling strength between oscillators. Assuming the coupling symmetry: β12=β21=β. We consider the followingcases:
-
Constant coupling (β = const):
β constant means that oscillators do not move and the coupling strength does not change.β = β12 = β21 = constant (3)
- Distance dependent coupling (β ≠ const):
β ≠ const, means that oscillators can move. We proposed that the coupling strength varies with the inverse of the square of the Euclidean distance ρ, between their spatial positions, (x(i)n,y(i)n,z(i)n), of the oscillators:
β ∝ ρ−2
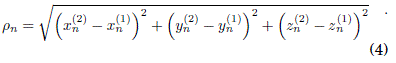
3.1 Existence Conditions
Taking into account that Dn must be defined in the interval [0, 1], and in order to avoid values out of range, we need to impose the conditions:
if Dn ≥ 1 ⇒ Dn=1
if Dn ≤ 0 ⇒ Dn=0
3.2 Abstract VectorIn order to study the oscillators' dynamics, we define the followingn-dimensional abstract vector, →V,
→
V(i) =f (D(i)n,ρn) , i=1,2 ,(5)
where D(i)n represents the i-th oscillator dynamics and ρn the Euclidean distance with respect to other oscillator. In this manner, we consider that each oscillator will be described by this new mathematical definition.
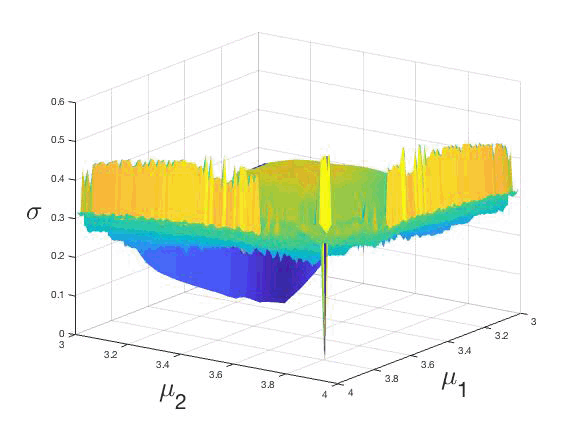
Figure 1: (Color online) Synchronizabilty actor σn in terms of the parameters μ1 and μ2, after n=106 time steps, or two coupled logistic maps defined in the interval [3,4] and being β = 0.0029.
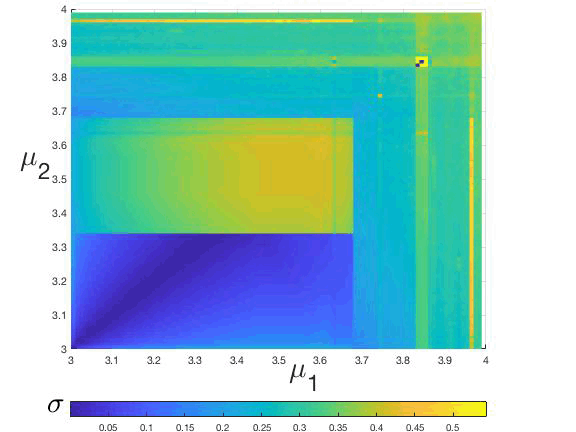
Figure 2: (Color online) Parameter plane (μ1, μ2), in terms of the synchrony actor σn whose values are related to the color bar.
3.3 Synchronizability actor
In order to quantify the general synchronization between two or more oscillators we define the synchronizability actor as:
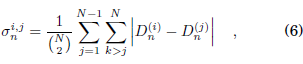
where in the case of two oscillators, as used by [42012Bustos-Espinoza & Ramírez-Ávila]:
![]()
There are many works dedicated to synchronization on coupled maps that use a synchronization actor as the indicator to characterize synchronization, e.g., several authors used the variance as such an indicator, i.e., ![]() to analyze coupled chaotic maps. Thus, [162004Lind et al.Lind, Corte-Real, & Gallas] adopt this indicator to study the coherence in scale-ree networks; [202005Masoller & MartíMasoller, & Martí] employ the variance to characterize the synchronous behavior of an array with random delays in the maps’ dynamics; [182006Lind et al.Lind, Nunes, & Gallas] use this indicator in networks with dierent topologies and considering delayed couplings. In this work, we characterize synchronization using Eq. (7) when σn → 0 or describing complete synchronization, in the same line of the usage of the variance as an indicator. Besides, we also consider the periodical oscillating behavior of σn as a manner to characterize phase-synchronization.
to analyze coupled chaotic maps. Thus, [162004Lind et al.Lind, Corte-Real, & Gallas] adopt this indicator to study the coherence in scale-ree networks; [202005Masoller & MartíMasoller, & Martí] employ the variance to characterize the synchronous behavior of an array with random delays in the maps’ dynamics; [182006Lind et al.Lind, Nunes, & Gallas] use this indicator in networks with dierent topologies and considering delayed couplings. In this work, we characterize synchronization using Eq. (7) when σn → 0 or describing complete synchronization, in the same line of the usage of the variance as an indicator. Besides, we also consider the periodical oscillating behavior of σn as a manner to characterize phase-synchronization.
3.4 Cases Studied
We considered three synchronous situations: complete synchronization and antisynchronization means a synchronization in phase and amplitude, while phase synchronization means a periodicity value or each synchrony actor considered. Thus, we define each case as a behavior of the synchronizability factor,
-
Complete synchronization: (σn → 0)
-
Complete Antisynchronization: (σn → 1)
-
Phase synchronization: (σn → oscillant)
3.5 Spatial Positions and Synchronization
followingour model, each oscillator can keep a fixed distance as long as we get a synchronization actor threshold, σnthreshold, indicating that the system tends toward complete synchronization; in that case, the oscillators turn on synchronized. We can express that act with the followingexpression:
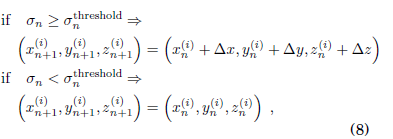
where ∆x, ∆y and ∆z, are small random displacements in the x, y and z directions respectively, followinga Gaussian distribution.
3.6 Noncollisional Condition
In order to avoid collisions between oscillators once we randomly generate their initial positions, we introduce the condition:
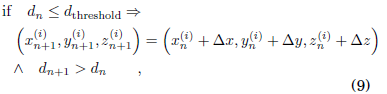
where dthreshold, is a threshold distance that ensures non-collision between oscillators, thus avoiding an infinite coupling strength.
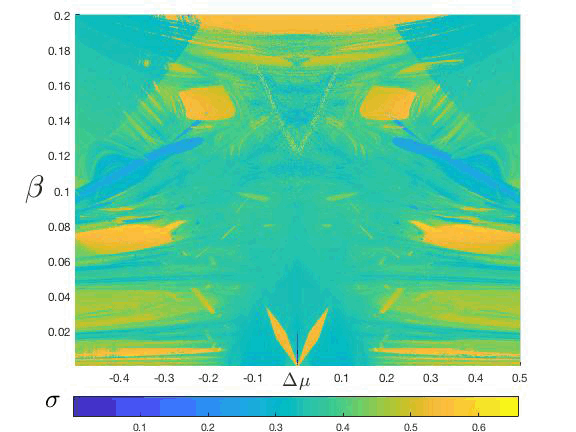
Figure 3: (Color online) Synchronization regions, obtained with μ(1)=μ(2)=3.83, in the plane coupling strength (β) vs. parameter mismatch (∆μ) and described in terms of the synchronizability, σ whose values are represented in the color bar, similar to that used in fig. 2. The central down part was reported by [32016Bustos-Espinoza & Ramírez-Ávila].
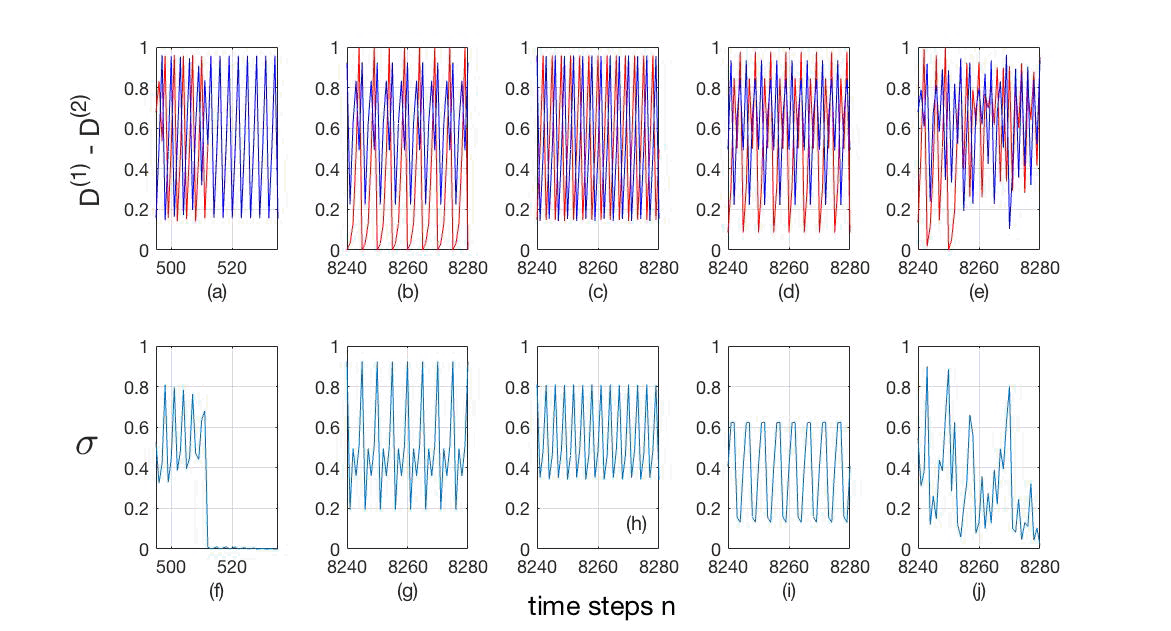
Figure 4: (Color online) (a)-(e) Time series of variables D(1) (blue) and D(2) (red), and ()-(j) synchronizability, σ: (a) and (): ∆μ = 0.0000, β = 0.0064, complete synchronization (σ→ 0); (b) and (g): ∆μ = 0.2045, β = 0.0342, phase synchronization (σP = 5); (c) and (h): ∆μ = 0.0220, β = 0.0128, phase synchronization (σP = 6); (d) and (i): ∆μ = 0.0695, β = 0.0128, phase synchronization (σP = 10); (e) and (j): ∆μ = 0.0685, β = 0.0545, chaos (σP → ∞).
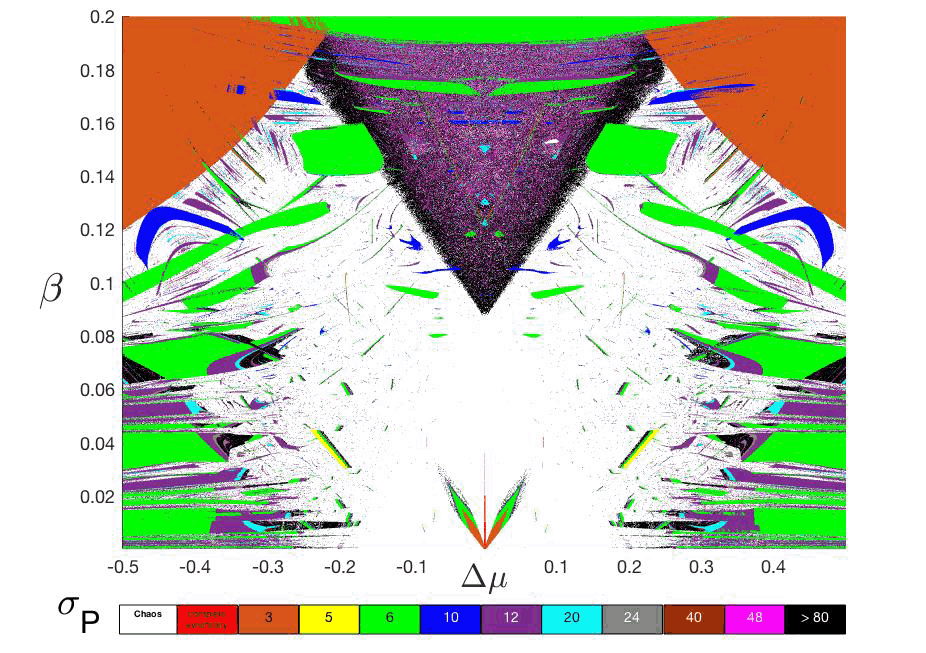
Figure 5: (Color online) Phase diagram: ∆μ vs. β in terms of σP. The horizontal color bar represents the main periodicities appearing in the synchronization regions and also the situation o non-synchronization (white=chaos). The darkness regions (black color) means periods greater than 80. It is important to underline a integer sequence of periods ound: 3, 5, 6, 10, 12, 20, 24, 40, 48, 80,... [32016Bustos-Espinoza & Ramírez-Ávila] reported the central down part.
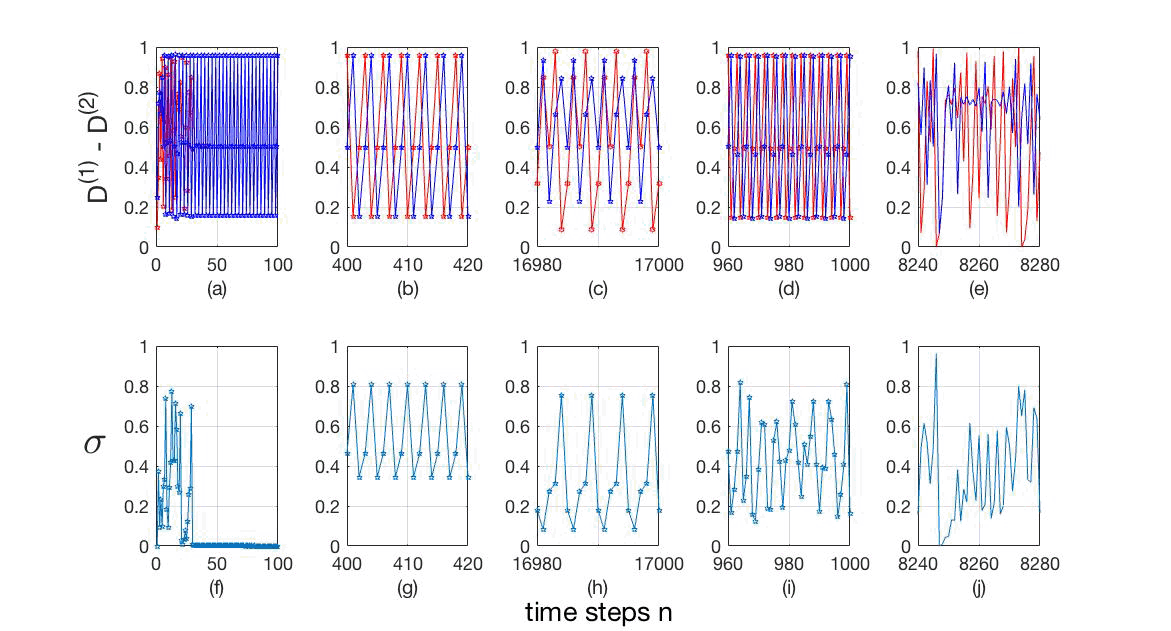
Figure 6: (Color online) Time series of (a)-(e) variables D(1) (blue) and D(2) (red), and ()-(j) synchronizability, σ: (a) and (): ∆μ = 0.0000, β = 0.0070, complete synchronization (σ→ 0); (b) and (g): ∆μ = 0.0100, β = 0.0050, phase synchronization (σP = 3); (c) and (h): ∆μ = 0.0855, β = 0.0085, phase synchronization (σP = 5); (d) and (i): ∆μ = 0.0260, β = 0.0154, phase synchronization (σP = 6); (e) and (j): ∆μ = 0.0770, β = 0.0565, chaos (σP → ∞).
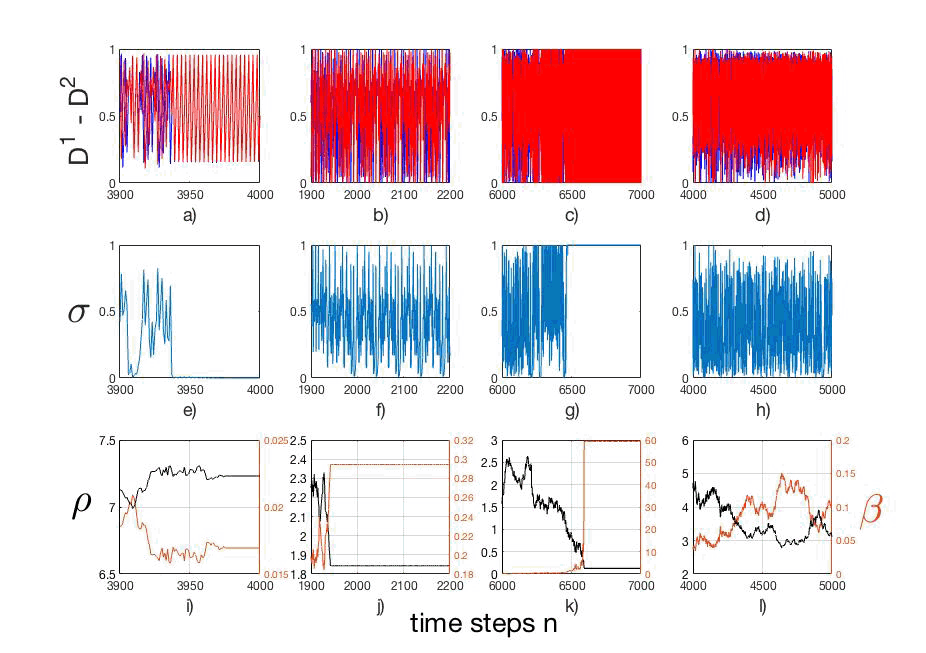
Figure 7: (Color online) Time series of, (a)-(d), the dynamical variables D(1) (blue) and D(2) (red); (e)-(h) thr synchronizability actor σ; (i)-(l) the relative distance ρ (black) and coupling strength, β (brown). The column (a), (e) and (i) illustrates complete synchronization, with initial conditions (i.c.): →V (1)0=(D(1)0,x(1)0,y(1)0,z(1)0) = (0.150,5.250,8.000,5.250); →V (2)0=(D(2)0,x(2)0,y(2)0,z(2)0) = (0.250,8.000,5.250,8.000); ρ = 1.900; (b), () and (j) show a phase synchrony, with i.c.: →V (1)0=(D(1)0,x(1)0,y(1)0,z(1)0) = (0.10,8.25,5.00,8.25); →V (2)0=(D(2)0,x(2)0,y(2)0,z(2)0) = (0.250,5.000,8.250,5.000); ρ = 1.900, with a period σP=48; (c), (g) and (k) show a anti-synchrony, with i.c.: →V (1)0=(D(1)0,x(1)0,y(1)0,z(1)0) = (0.100,5.000,5.000,5.000); →V (2)0=(D(2)0,x(2)0,y(2)0,z(2)0) = (0.250,8.300,8.756,8.000); ρ = 0.2, with a period σP=2; (d), (h) and (l) show a chaotic situation, with i.c.: →V (1)0=(D(1)0,x(1)0,y(1)0,z(1)0) = (0.150,5.250,8.000,5.250); →V (2)0=(D(2)0,x(2)0,y(2)0,z(2)0) = (0.250,8.000,5.250,8.000); ρ = 1.900, with a period σP → ∞. All pics with μ1=μ2=3.830.
3.7 Synchronization Regions
Our system is composed of two coupled logistic maps. To study the synchronization regions in the parameter plane, we determine a correlation between, coupling strength β, parameter mismatch ∆μ and σn. And the most important and "new" approach: β vs. parameter mismatch ∆μ, and the σ-periodicities.
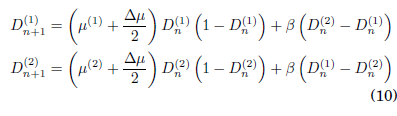
4 RESULTS
We can characterize the synchronization of the system followingthe model described in Sect. 3, revealing the synchronizability or synchronization actor σ in terms of the parameters, i.e., μ(1)−μ(2), where σ, has been computed taking the mean over the last 700 values. The parameters μ(i), (i=1,2) where or simplicity, we adopt the notation μ(i)=μi, are defined in the interval [3,4], regions where the logistic coupled maps can exhibit regular or chaotic behavior, as was reported by [42012Bustos-Espinoza & Ramírez-Ávila]. In fig. 1, we show a three-dimensional insight μ1 − μ2 − σ that represents the surface generated after n = 106 time steps, and considering a coupling strength, β = 0.0029. The projection of fig. 1 onto the plane μ1 − μ2 (the parameter plane) is shown in fig. 2, where the color code is related to the value of σ. Both from igs. 1 and 2, it is easy to identify a remarkable point or which σ plummets to zero. This point corresponds to μ1=μ2=3.83. In what it follows, we will consider these values of μi as referential ones to describe the dynamical behavior of the coupled maps when the parameter mismatch (∆μ) is increased. The computation of the σ values when varying the coupling strength (β) and ∆μ results in constructing the phase diagram of the system after an extensive analysis of the periodicities.
4.1 Constant Coupling
In order to find the synchronization regions or the system of two coupled logistic map, we follow the model explained in Sect. 3, i.e., β = const or nonmoving oscillators. We recompute the synchronizability σ using Eq. (10) and introducing the parameter mismatch ∆μ = μ1−μ2, i.e., when both oscillators are identical ∆μ = 0 or they are nonidentical ∆μ ≠ 0. We chose an ample interval of coupling strength values, β, obtaining a new parameter plane given by β vs. ∆μ and depicted in terms of the σ-values shown in fig. 3, where it is notable the symmetry manifested or the quadratic form of the logistic maps.
To know more about the dynamics of the system, we choose some points inside some regions of fig. 3 or obtaining the evolution of the dynamical variables, D(i), (i=1, 2), and their corresponding σn time series shown in fig. 4(a)-(e) and fig. 4()-(j) respectively.
From fig. 4(a) we observe that the signals are completely synchronized, i.e. our quantifier of the phenomenon, σ, goes to zero (σ→ 0) as it is shown in fig. 4(). In igs. 4(b)-(d), we can see that the time series are in phase synchronization, whose synchronizability actor oscillates with a well defined period, shown in igs. 4(g)-(i). finally, in igs. 4(e) and (j) the time series exhibit a chaotic behavior and their synchronizability σ oscillates without any specific period. Time series of (a)-(e) variables D(1) (blue) and D(2) (red), and ()-(j) synchronizability, σ, are: (a) and (): ∆μ = 0.0000, β = 0.0064, complete synchronization (σ→ 0); (b) and (g): ∆μ = 0.2045, β = 0.0342, phase synchronization (σP = 5); (c) and (h): ∆μ = 0.0220, β = 0.0128, phase synchronization (σP = 6); (d) and (i): ∆μ = 0.0695, β = 0.0128, phase synchronization (σP = 10); (e) and (j): ∆μ = 0.0685, β = 0.0545, chaos (σP → ∞).
4.2 Periodicities
To have a deeper insight of the system's dynamical properties, we analyze the parameter plane by measuring the periods of the synchronizability, σP taking the mean over the last 500 values of each σ. With this technique we obtain a new extended parameter plane, β vs. ∆μ described in terms of the periodicities σP, shown in fig. 5, where the horizontal color bar represents the main periodicities appearing in the synchronization regions. The extreme cases, complete synchrony and chaos, are defined as that they do not have any periodicity because the synchronizability in these cases remains stable or oscillates chaotically, respectively. Note that the symmetry and the relevant regions of apparent same σ values in fig. 5. Another interesting issue ound in the upper part of fig. 5, below the orange region with periodicity 3, is the presence of regions with similar shapes to those ound by [262011Ramírez-Ávila & GallasRamírez,& Gallas] in the parameter space of the Tinkerbell map.
To test the system we choose some points inside specific regions or evaluating the dynamic variables, D(i), and their corresponding synchronizability σ, as we can see in fig. 6(a)-(e) and fig. 6()-(j) respectively. The time series of the variables D(1) and D(2) are represented in blue and red respectively. The chosen points (∆μ,σ) were: (0.0000, 0.0070), showing complete synchronization, i.e. σ→ 0; (b) and (g): (0.0100,0.0050), exhibiting phase synchronization, with σP = 3; (c) and (h): (0.0855, 0.0085), also displaying phase synchronization, with σP = 5; (d) and (i): (0.0260, 0.0154), also showing phase synchronization, with σP = 6; and finally (e) and (j): (0.0770, 0.0565), illustrating chaotic behavior, without any specfiic periodicity. Note the integer sequence of periods: 3, 5, 6, 10, 12, 20, 24, 40, 48, 80, 96,...
4.3 Integer Sequence of Periods
We ound the integer sequence of periods: 3, 5, 6, 10, 12, 20, 24, 40, 48, 80, 96, ..., might be described by the recurrent integer sequence relation given by Eq. (11), with a new seed, i.e., P(1)=3 and P(2)=5, dierent of what was ound by [12009Brockhaus]. We do not include the extreme cases of complete synchronization and chaos.
P (n) = 2 P(n−2) (n > 2); P(1)=3, P(2)=5 (20)
4.4 Distance dependence
As we proposed in Sect. 3, synchronization depends on the magnitude of the coupling strength, β, i.e., we can consider a system where the oscillators can move according to Eqs. (8) and (9); that means a permanent change in the spatial positions before they can synchronize. In several cases, movement tends to facilitate synchronization, as was pointed out by [42012Bustos-Espinoza & Ramírez-Ávila].
In this work, we study an amplified parameter plane in order to confirm i the movement enhances or not the synchronization. To this end, we study the abstract vector →V, defined in Eq. (5), i.e., the dynamical variables, D(i), (i=1,2), the relative distance between oscillators, ρ, altogether with their correspondent coupling strength, β ∝ ρ−2 and the synchronizability actor, σ, the whole as a unction of time n. The results are shown in a matrix of graphs shown in fig. 7, where we can check the time series of the dynamical variables D(1) (blue) and D(2) (red), in fig. 7(a)-(d); the synchronizability σ in fig. 7(e)-(h), and the relative distance, ρ (black) and the coupling strength, β (brown) in fig. 7(i)-(l). Drawing attention to the columns, the one igs. 7(a), (e) and (i) describing the situation of complete synchronization, with the initial conditions (i.c.): →V (1)0=(D(1)0,x(1)0,y(1)0,z(1)0) = (0.15,5.250,8.000,5.250); →V (2)0=(D(2)0,x(2)0,y(2)0,z(2)0) = (0.250,8.000,5.250,8.000); a threshold distance, dthreshold=ρ = 1.900; (b), () and (j) shown a phase synchrony, with i.c.: →V (1)0=(D(1)0,x(1)0,y(1)0,z(1)0) = (0.10,8.250,5.000,8.250); →V (2)0=(D(2)0,x(2)0,y(2)0,z(2)0) = (0.25,5.000,8.250,5.00); with a threshold distance, ρ = 1.900, and a periodicity value, σP=48. In the situation shown in (c), (g) and (k) we decrease the threshold distance, ρ = 0.2 in order to get an anti-synchronization, i.e., Dn(1)+Dn(2)=1, with i.c.: →V (1)0=(D(1)0,x(1)0,y(1)0,z(1)0) = (0.10,5.000,5.000,5.00); →V (2)0=(D(2)0,x(2)0,y(2)0,z(2)0) = (0.25,8.300,8.756,8.00). In this column the dynamic oscillation goes from 0 to 1 repeating a ew times (n=118); and finally, (d), (h) and (l), shown a chaos situation, with i.c.: →V (1)0=(D(1)0,x(1)0,y(1)0,z(1)0) = (0.15,5.250,8.000,5.25); →V (2)0=(D(2)0,x(2)0,y(2)0,z(2)0) = (0.25,8.000,5.250,8.000); a threshold distance, ρ = 1.900, with a periodicity σP → ∞. All pics were calculated with μ1=μ2=3.830
5 Conclusions and perspectives
Using the proposed model and the extended domain of our parameters we get an amplified new synchronization region, where we apply the periodicity technique, reported by [32016Bustos-Espinoza & Ramírez-Ávila], in order to get a new phase diagram. It was possible to identify a natural sequence of integers (periods) that appear on our map, this sequence comes from a bifurcation cascade into the parameter plane, exiting a chaotic window and going to another chaotic region in a system of two coupled logistic maps whose dynamical behavior in terms of their integer periodicities, follows a recurrence relation with a new seed, a dierent to that ound by [12009Brockhaus], who combine the series, P(n)=3 ×2n and P(n)=5 ×2n, but without initial term 3 in the one.
In our study of static and dynamic situations, we find in both cases other types of synchronization besides the complete one, i.e. phase and anti synchronization. The abstract vector, which includes dynamics and spatial positions, enables us to understand in a deeper way the dynamical aspects related to synchronization in this type of system. Another important result is the confirmation that movement tends to enhance synchronization.
Our comprehensive study on the synchronization of coupled logistic maps using periodicities, allowed us to find synchronization regions with shapes very dierent to the typical Arnold tongues and with the feature that due to the knowledge of periods, the determination of the so-called winding numbers is done. The huge interval of coupling strength values considered in this work might be essential information in the situation in which the oscillators are moving. This knowledge permits us to know instantaneously whether the oscillators are located in positions allowing synchronization. The method to detect synchronization developed here might be extended to systems with many coupled maps and organized under dierent topologies similar to those studied by [172004aLind et al.Lind, Gallas & Herrmann,182006Lind et al.Lind, Nunes, & Gallas]. Moreover, our method might also be used or detecting synchronization in other kinds of maps, or instance, in cubic maps exhibiting bistability as those studied by [162004Lind et al.Lind, Corte-Real, & Gallas] or multistability as in the case o coupled trios o Rulkov maps considered by [102019Iglesias & Ramírez-Ávila]. finally, it is possible to use other potentials according to the type of movement and interaction between the oscillators, as the Lennard-Jones potential that models sot attractive, and repulsive interactions.
Conflict of interests Authors declare that there is no conlict of interest with respect to the publication of this document.
References
Brockhaus, K. 2009 in The On-Line Encyclopedia of Integer Sequences (A164095), available in https://oeis.org/A164095
Burgoa, K. L., & Nogales, J. A. C. 2001, Revista Boliviana de Física, 7, 51 [ Links ]
[32016Bustos-Espinoza & Ramírez-Ávila]
Bustos-Espinoza, R. O. E., & Ramírez-Ávila, G. M. 2016, The European Physical Journal Special Topics, 225, 2697 [ Links ]
[42012Bustos-Espinoza & Ramírez-Ávila]
Bustos-Espinoza, R. O. E., & Ramírez-Ávila, G. M. 2012, Revista Boliviana de Física, 22, 1 [ Links ]
[52017Calderón de la Barca, & Ramírez-Ávila]
Calderón de la Barca, I., & Ramírez-Ávila, G. M. 2017, Revista Boliviana de Física, 30, 1 [ Links ]
Chaté, H., & Manneville, P. 1988, Physica D, 32, 409 [ Links ]
Chua, L. 1993, Journal of Circuits, Systems and Computers, 3, 93
Fujisaka, H., & Yamada, T. 1983, Progress of Theoretical Physics, 69, 32
[92011ujiwara et al.ujiwara, Kurths, & Díaz-Guilera]
ujiwara, N., Kurths, J., & Díaz-Guilera, A. 2011, Physical Review E, 83, 025101
[102019Iglesias & Ramírez-Ávila]
Iglesias, K., & Ramírez-Ávila, G. M. 2019, Revista Boliviana de Física, 34, 3 [ Links ]
Kaneko, K. 1985, Progress of Theoretical Physics, 74, 1033
[121987Kuramoto & NishikawaKuramoto, & Nishikawa]
Kuramoto, Y., & Nishikawa, I. 1987, Journal of Statistical Physics, 49, 569
Kocarev, L. (Ed.) 2013, Consensus and Synchronization in Complex Networks (Berlin: Springer) [ Links ]
[142011Garcóa-Cantú et al.Garcóa-Cantú, Antonopoulos, & Basios]
Garcóa-Cantú, A., Antonopoulos, Ch G., & Basios, V. 2011, Chaos, Solitons & ractals, 44, 574
[152016L'Her et al.L'Her, Amil, Rubido, & Martí]
L'Her, A., Amil, P., Rubido, N., Martí, A. C., & Cabeza, C. 2016, The European Physical Journal B, 89, 81 [ Links ]
[162004Lind et al.Lind, Corte-Real, & Gallas]
Lind, P. G., Corte-Real, J., & Gallas, J. A. C. 2004, Physical Review E, 69, 026209 [ Links ]
[172004aLind et al.Lind, Gallas & Herrmann]
Lind, P. G., Gallas, J. A. C., & Herrmann, H. J. 2004, Physical Review E, 70, 056207 [ Links ]
[182006Lind et al.Lind, Nunes, & Gallas]
Lind, P. G., Nunes, A., & Gallas, J. A. C. 2004, Physica A, 371, 100 [ Links ]
[192001Masoller et al.Masoller, Cavalcante, & Rios Leite]
Masoller, C., Cavalcante, H. L. D., & Rios Leite, J. 2001, Physical Review E, 64, 037202 [ Links ]
[202005Masoller & MartíMasoller, & Martí]
Masoller, C., & Martí, A. C. 2001, Physical Review Letters, 94, 134102-4 [ Links ]
Matsumoto, T. 1984, IEEE Transactions on Circuits and Systems, 31, 1055 [ Links ]
May, R. 1976, Nature, 261, 459 [ Links ]
[232001Pikovsky et al.Pikovsky, Rosenblum, & Kurths]
Pikovsky, A., Rosenblum, M., & Kurths, J. 2001, Synchronization, A Universal Concept in Nonlinear Sciences (Cambridge: Cambridge University Press) [ Links ]
Ramírez-Ávila, G. M., Guisset, J. L., & Deneubourg, J. L. 2003, Phyisca D: Nonlinear Phenomena, 182, 254 [ Links ]
[252006Ramírez-Ávila et al.Ramírez, Guisset, & Deneubourg]
Ramírez-Ávila, G. M., Guisset, J. L., & Deneubourg, J. L. 2006, Revista Boliviana de Física, 12, 1 [ Links ]
[262011Ramírez-Ávila & GallasRamírez,& Gallas]
Ramírez-Ávila, G. M.,& Gallas, J. A. C. 2011, Revista Boliviana de Física, 19, 1 [ Links ]
[272014Schultz et al.Schultz, Heitzig, & Kurths]
Schultz, P., Heitzig, J., & Kurths, J. 2014, New Journal of Physics, 16, 125001
[282017Subieta-ríos & Ramírez-Ávila]
Subieta-ríos, V. & Ramírez-Ávila, G. M. 2017, Revista Boliviana de Física, 31, 3
Sun, H., & Cao, H. 2016, Communications in Nonlinear Science and Numerical Simulation, 40, 15 [ Links ]
[301983Tang et al.Tang, Mees, & Chua]
Tang, Y., Mees, A., & Chua, L. 1983, IEEE Transactions on Circuits and Systems, 30, 620 [ Links ]
Verhulst, P. 1838, Correspondance Mathématique et Physique, 10, 113 [ Links ]
Yamada, T., & Fujisaka, H. 1983, Progress of Theoretical Physics, 70, 1240