ARTÍCULOS

 

DINAMICA SEMICLÁSICA DE ENLACE FUERTE EN CAMPOS RAPIDAMENTE OSCILANTES MÁS UN POTENCIAL ESTÁTICO ARBITRARIO*

SEMICLASSICAL TIGHT-BINDING DYNAMICS IN RAPIDLY OSCILLATING FIELDS PLUS A STATIC ARBITRARY POTENTIAL

 

 

L. A. Martínez', D. Sanjinés'', & J. P. Gallinar^'
' Departamento de Física, Universidad Simon Bolívar Apartado 89000, Caracas 1080A
Venezuela &
^'' Instituto de Investigaciones Físicas, Carrera de Física
Universidad Mayor de San Andres
c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8635 La Paz - Bolivia
^*Traduccion autorizada de "Semiclassical tight-binding dynamics in rapidly oscillating fields plus a static arbitrary potential", Martínez L. A., Sanjines D. and Gallinar J.-R, International Journal ofModern Physics B 28 (2014) 1450173.

 

 

---

Investigamos la dinamica semiclásica inducida en una red unidimensional de enlace fuerte por un campo electrico inhomogéneo de alta frecuencia ω, mas un potencial estático arbitrario. Encontramos, -de manera analoga al caso del péndulo de Kapitza- un potencial efectivo independiente del tiempo que describe el movimiento electronico promedio hasta un orden de ω^-2. Este potencial efectivo depende de: el potencial estatico externo, la constante de red y el campo electrico aplicado de alta frecuencia. Encontramos, notablemente, que la correccion dinámica debida al campo rápidamente oscilante es formalmente idéntica a aquella asociada al pendulo de Kapitza en el régimen del continuo. Finalmente, los resultados de este trabajo se aplican a: el oscilador armonico en la red, el efecto de la oscilación Bloch y fenomenos de "localización dinámica" en arreglos de fibras ópticas (donde hacemos una prediccion experimental).

Codigo(s) PACS: 42.50.Ct — 42.50.Hz — 03.65.Sq

Descriptores: Hamiltoniano efectivo — Modelo semiclasico — Modelo de enlace fuerte

---

Abstract

We investigate a semiclassical dynamics driven by a high-frequency ω inhomogeneous field, plus a static arbitrary potential on a one-dimensional tight-binding lattice. We find -in the approach of Kapitza's pendulum- an effective, time independent potential that describes the average of the electronic motion to order ω^-2. This effective potential depends on the static external potential, on the lattice constant and on the applied high frequency field. Remarkably, we find that the dynamic correction of rapidly oscillating fields is formally identical to that associated to Kapitza's usual continuum result. Finally, applications are made to: the harmonic oscillator on the lattice, the Bloch oscillation effect and "dynamical localization" in arrays of optical waveguides (wherein an experimental prediction is made).

Subject headings: Effective Hamiltonian — Semiclassical model — Tight-binding model

---

 

 

1. INTRODUCCIÓN

El estudio del movimiento electronico y de los estados electronicos definidos en espacios discretos o en redes es un asunto de considerable importancia dadas sus aplicaciones en física (Papp & Micu 2007; Mattis 1986; Itin & Neishtadt 2014). Como tales, fenomenos reticulares típicos como las oscilaciones de Bloch (Bloch 1928; Hartmann et al. 2004), localización dinámica (Dunlap & Kenkre 1986; Holthaus & Hone 1996), efectos de estrechamiento de banda (Papp & Micu 2007), localización asintótica (Sanjines & Gallinar 2001), aumento de la masa ex-citonica (Mattis 1986; Mattis & Gallinar 1984), y otros, han sido exhaustivamente estudiados tanto cuanticamente como semiclásicamente (Ashcroft & Mermin 1976), donde este ltimo modelo permite tratar de manera mas sencilla los efectos combinados en el movimiento electronico de campos eléctricos aplicados inhomogeneos y campos dependientes del tiempo. En los dispositivos nanoscopicos (Papp & Micu 2007), tanto la naturaleza de enlace fuerte de las bandas (Gallinar & Mattis 1985) como la in-homogeneidad de los campos puede ser importante para simular el confinamiento cuantico de los estados electronicos. Además, a fin de aumentar el interes en estos fenómenos, se sabe que un paquete de ondas fotonico en un arreglo de guías de onda (Dreisow et al. 2011; Longhi 2007) puede simular el comportamiento de un electron de Bloch moviéndose en una banda de enlace fuerte bajo la influencia de campos electromagneticos adecuados (Longhi 2007). Ello es una consecuencia de la "ecuación óptica de Schrodinger" (Marte & Stenholm 1997), donde se da una analogıa formal entre la variable temporal en la ecuación de Schrodinger dependiente del tiempo (para el electron de Bloch en la red) y la variable espacial en la "ecuación óptica de Schrodinger" a lo largo del eje longitudinal del arreglo optico (para el paquete de ondas fotonico). De esta forma, los fenomenos dinámicos cuánticos de la partícula en una red son "mapeados" a lo largo del eje de un arreglo de fibras opticas donde se observa una distribucion estática de intensidad luminosa. Así, los fenomenos oscilación de Bloch (Lenz 1999) y localización dinámica (Longhi et al. 2006) han sido observados; recientemente, el fenomeno de localización asintotica (Sanjinés & Gallinar 2001) fue asimismo confirmado experimentalmente (Dreisow et al. 2011) en un arreglo de fibras opticas con un perfil de curvatura cubico. Recientemente se han logrado avances importantes (tanto teoricos como experimentales) en la fısica de los arreglos de fibras ópticas (Garanovich et al. 2012); dichos arreglos opticos surgen pues como simuladores cuanticos "bona fide" en el sentido referido en revisiones recientes (Buluta & Nori 2009; Georgescu et al. 2014). Existen entonces algunos escenarios específicos donde es posible buscar aplicaciones experimentales para los resultados teoricos que se presentan en este trabajo, por ejemplo, el que se propone en la seccion 4.

Así, despues de revisar brevemente algunos de los fenomenos más interesantes que surgen en el contexto del modelo de enlace fuerte, describiremos a continuacion el plan a ser desarrollado en este trabajo. Nos proponemos generalizar el tratamiento conocido que hace Kapitza del pendulo invertido (Kapitza 1951) al caso de los campos inhomogeneos (Longhi 2007) en la aproximacion semiclásica de enlace fuerte (Ashcroft & Mermin 1976). Se sabe que para una ley de dispersion cuadrática, el método de Kapitza se suele emplear (en el límite de altas frecuencias ω → ∞) (Bandyopadhyay & Dattagupta 2008) para estudiar, por ejemplo, el confinamiento de "atomos frios" (entre otros) en un potencial efectivo independiente del tiempo. Adaptaremos entonces el metodo de Kapitza a una banda de enlace fuerte con interaccion a primeros vecinos, y de esta forma ser capaces de contrastar nuestros resultados con aquellos que surgen usualmente bajo el modelo de una banda cuadratica. En particular, hallamos que debido a la presencia de la red el potencial efectivo U_eff(X) (Cf. Ec. 26) depende cuadraticamente del potencial estatico U(X), en contraste con la dependencia lineal que se halla usualmente (Bandyopadhyay & Dattagupta 2008; Rahav et al. 2003). Hallamos ademas que la corrección dinámica (que varía como ω⁻² para ω → ∞) es formalmente similar a la que se obtiene por el metodo de Kapitza en el regimen del continuo. Y aún más, el potencial efectivo U_eff(X) depende también de la posición y el pseudo-momentum iniciales, en contraste con los resultados equivalentes que se halla con el metodo de Kapitza.

En resumen, y a fin de contrastar los procedimientos, en la seccin II presentamos la deduccion de la formula para el potencial efectivo (Cf. Ec. 26), donde los detalles de esta deduccion se completan en los apendices A y B. En el apéndice C se invoca el teorema de Kroopnick (Kroopnick 1972) para establecer la condicion suficiente para que la magnitud de X(t) permanezca acotada cuando t → ∞. En el apendice D se hace una aplicación al caso del "oscilador armonico" en la red, caso que fue tratado previamente en la literatura (Longhi 2007; Gallinar & Chalbaud 1991). Finalmente, en el apendice E se presentan formulas para obtener las frecuencias de pequeñas oscilaciones en torno a los mínimos del potencial efectivo U_eff(X).

 

2. DEDUCCION DE LA FÓRMULA PARA EL POTENCIAL EFECTIVO

Las ecuaciónes semiclasicas canónicas de movimiento (Ashcroft & Mermin 1976) para un electron de enlace fuerte moviéndose en una dimension bajo la influencia de un potencial estático U(x) y de un campo electrico rápidamente oscilante f(x, t), estan dadas por

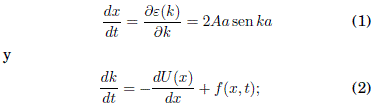
donde A es el elemento de matriz de "salto" (hopping) proporcional al ancho de banda, a es la constante de red, k es el pseudo-momento critalino (tomaremos ~ = 1 en este trabajo) y, finalmente, ε (k) = 2A(1 - cos ka) es la ley de dispersion de enlace fuerte. El campo rapidamente oscilante f(x,t) se puede expresar como una serie de Fourier:

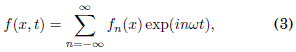
donde f_n(x) es la n-esima componente de Fourier del campo electrico f(x, t) de alta frecuencia ω. Por simplicidad suponemos f_n(x) = f_-n(x), de tal forma que f(x,t) es una funcion real y par con respecto al tiempo t. En nuestro sistema, la frecuencia lo se supone mucho mayor que cualquiera de las frecuencias asociadas a la naturaleza del potencial estatico U(x). Es mas: el promedio temporal sobre el periodo T = de f(x,t) se toma igual a cero, i.e., hf(x,t)i = f0(x) = 0. Siguiendo el formalismo de Kapitza (Kapitza 1951), escribimos x(t) y k(t) como

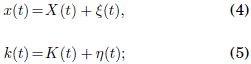
donde y representan las partes pequeñas y rapidamente oscilantes de la posición x(t) y del pseudo-momentum k(t) respectivamente, con promedios temporales () = () = 0. Sustituyendo las Ecs. (4) y (5) en las Ecs. (1) y (2) respectivamente, se tiene que:

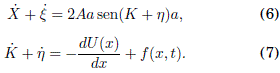
Si se expande dU/dx y f(x,t) en terminos del parametro pequeño , se obtiene a primer orden en que

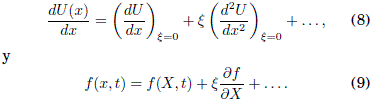
La sustitucion de las Ecs. (8) y (9) en la Ec. (7) resulta en

hasta primer orden en . En la Ec. (10) aparecen dos grupos de terminos con características diferentes: terminos rápidamente oscilantes y términos que no estan perturbados; ambos grupos deben entonces ser iguales por separado. Para los terminos oscilatorios podemos escribir

pues los terminos en la Ec. (10) que contienen son pequenos comparados con el que aparece en la Ec. (11). Promediando los terminos restantes en la Ec. (10) sobre un periodo, obtenemos

Donde

Procedemos ahora con la Ec. (6); expandiendola obtenemos

de donde se separa (como en la Ec. (10)) los terminos rapidos y lentos; para la parte rápida se obtiene

y promediando la parte lenta sobre un periodo resulta

donde A continuacion integramos la Ec. (11) y la Ec. (14) (considerando a X(t) y a K(t) como "constants" sobre la escala temporal de T), obteniendo de que

Para integrar la Ec. (14) aproximamos a primer orden , y de la Ec. (14) obtenemos

Se puede mostrar que las Ecs. (12) y (15) son de la forma hamiltoniana con respecto a las variables lentas X(t) y K(t), con un hamiltoniano efectivo

donde son las ecuaciónes canonicas de movimiento. Estas ecuaciónes se deducen a partir de las relaciones que se muestran en los apendices A y B:

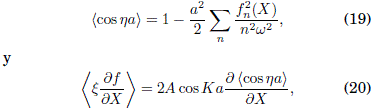
respectivamente. Ya que H(X, K) no depende explícitamente del tiempo entonces es una constante de movimiento que representa a la "energía" efectiva de la partcula correspondiente a su movimiento promedio evaluado en las condiciones iniciales X₀ y K₀.

A continuacion calculamos el potencial efectivo U_eff(X) a traves de la definición

donde m es la masa efectiva de enlace fuerte dada por m = 1/(2Aa²). Ya que de acuerdo a la Ec.(15) se tiene , entonces

Sustituyendo en la Ec. (22) los valores de y dados por las Ecs. (12) y (15) respectivamente, obtenemos

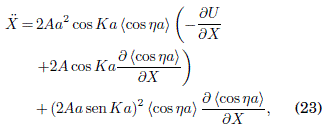
de donde sigue una notable simplificacion debida a la identidad cos² Ka + sen² Ka = 1. El resultado es

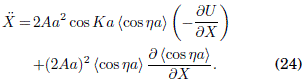
Expresando en la Ec. (24) el termino que contiene a a traves de la ley de conservación de la energía efectiva E (Cf. Ec. (B4)), obtenemos ; despreciando en la Ec. (24) los terminos del orden de O(ω^-4), obtenemos finalmente para la aceleracion

la integral con respecto a X da

que es la expresion final que obtenemos para el potencial efectivo.

Aunque los resultados centrales de este trabajo (Ecs. (25) y (26)) se dedujeron para un hamiltoniano de enlace fuerte con interacciones a primeros vecinos solamente, la extension del método que presentamos aquí para incluir interacciones a segundos vecinos se puede realizar de manera directa al sustituir la Ec. (1) por , donde B es el elemento de matriz de "salto" correspondiente a las interacciones a segundos vecinos. La consecuencia de este calculo en el potencial efectivo debe llevar a las mismas conclusiones que las anunciadas por Itin y Neishtadt (Itin & Neishtadt 2014) acerca del efecto combinado debido a campos externos oscilatorios y campos no-uniformes.

 

3. APLICACION AL OSCILADOR ARMÓNICO FORZADO EN LA RED

Consideremos el movimiento del oscilador armonico en la red (Longhi 2007; Gallinar & Chalbaud 1991) sujeto ademas aun campo armónico de alta frecuencia. Tomemos U(x) = kx²/2 en la Ec.(26) y f(x,t) = -kxcosωt, por simplicidad, a fin de obtener el potencial efectivo U_eff(X) dado por

donde n es la constante elastica del oscilador. Adoptamos la unidades físicas en las que ka²/8 = 1 es la energa y el inverso del tiempo, y a es la longitud y el inverso del momentum; tomamos como condiciones iniciales X = X₀ y K = 0. En dichas unidades fısicas especiales, la Ec. (27) se convierte en

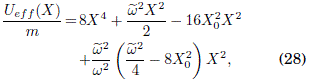
donde . Así, el potencial efectivo U_eff(X) depende, entre otros, de la posicion inicial X_o y de la frecuencia ω. Para X₀ < , U_eff(X) tiene un mınimo en X = 0; para X₀ > , U_eff(X) tiene dos mínimos en

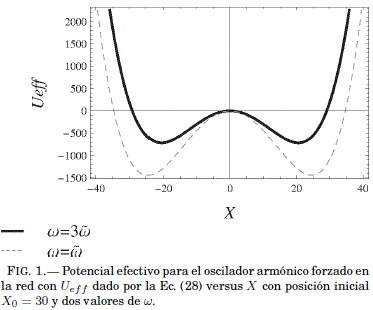
Como se puede ver en la Fig. 1, la distancia entre estos mínimos aumenta al disminuir ω, tal como lo predice la Ec. (29). Debido a la estructura matematica de U_eff(X) en la Ec. (28), la partıcula puede oscilar en dos regímenes diferentes: "el regimen de Bloch" (Gallinar & Chalbaud 1991) donde U_eff(X) tiene dos mınimos y la partcula oscila en alguno de ellos, y "el regimen del continuo" (Longhi 2007; Gallinar & Chalbaud 1991) donde la partícula o bien visita ambos mínimos, o bien oscila en torno a un mínimo en X = 0 cuando X₀ < . Estos regímenes estan separados por la condición de bifurcacion dada por

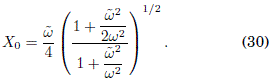
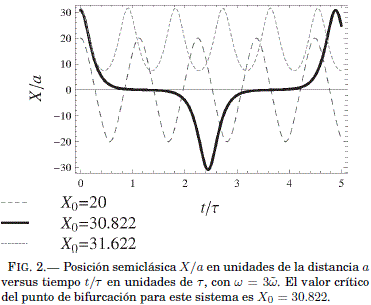
Para ω → ∞, la Ec. (30) lleva a X₀ = como condicion de bifurcación en ausencia del campo forzador armonico de alta frecuencia. En la Fig. 2 se muestra las soluciones numericas de la Ec. (25), donde se puede distinguir ambos regímenes con X₀ = = 30.822... como el punto de bifurcacion entre ellos.

Finalmente, obtenemos la expresion para la frecuencia de la partícula cuando oscila en el regimen de Bloch en torno a los mínimos de U_eff(X); usamos para ello , obteniendose

donde la frecuencia efectiva aumenta en presencia

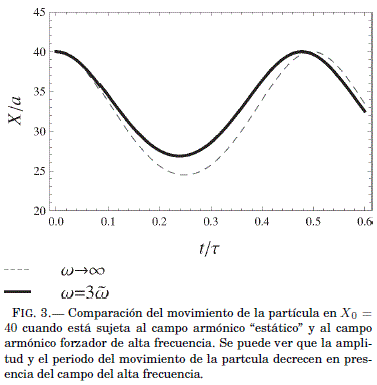
del campo rapidamente oscilante. Este incremento en la frecuencia efectiva se verifica al comparar numericamente la solución X(t) del caso estatico con la solucion respectiva para el caso , X₀ = 40, que se muestra en la Fig. 3.

 

4. APLICACION A FENÓMENOS DE LOCALIZACIÓN PREDICCION EXPERIMENTAL DE "LOCALIZACIÓN DINAMICA" EN ARREGLOS DE FIBRAS ÓPTICAS

Considerese el hamiltoniano de enlace fuerte H(x,p) = -2A cos ap + U(x,t) (con p = ) cuyos eigenvalores ε(k) constituyen la ley de dispersion para la velocidad semiclásica dada en la Ec. (1); el potencial dependiente del tiempo U(x,t) = U(x) - ya contiene al potencial estatico U(x) y al campo oscilante f(x,t) que aparecen en la "fuerza" semiclasica en la Ec. (1). En este escenario físico ocurren los fenomenos de "localización" de un electron en una red unidimensional tal como lo refirieron Dunlap y Kenkre (Dunlap & Kenkre

1986): si la proyeccion del desplazamiento cuadrático medio en la red permanece acotado cuando t → ∞, entonces la partícula estara localizada (esta condición implica asimismo que el valor medio de la posición también permanece acotado). En las expresiones anteriores es la funcion de onda que resuelve la ecuación de Schrödinger; son las funciones de Wannier que estan localizadas en torno a los sitios de la red con posiciones x = na (para n entero). Los casos relevantes de localización que fueron reportados en la literatura corresponden a los siguientes potenciales: (i) oscilacion de Bloch (Bloch 1928; Hartmann et al. 2004) cuando U(x,t) = x; (ii) localización dinámica AC (Dunlap & Kenkre 1986; Holthaus & Hone 1996) cuando U(x,t) = x cos ωt (J₀(/ω) = 0) y localización dinámica AC+DC (Holthaus & Hone 1996; Zhao 1991) cuando ; localización asintótica (Sanjinés & Gallinar 2001) cuando U(x, t) = xt. Las condiciones de localización en el caso (ii) se hallan entre parentesis.

La definicion de localización puede relacionarse con la definicion de "acotamiento" de una función y(t) que resuelve la ecuacin diferencial ordinaria, autonoma y -en general- no-lineal = g(y), i.e., no debe diverger. Ya que esta ecuación se puede escribir como , entonces la condicion de acotamiento para y(t) esta dada por el teorema de Kroopnick (apendice C), donde y(t) se identifico al describir el esquema de Kapitza (seccion 2) con nuestra posición media X(t) que varía lentamente en . Esto su vez nos permite realizar la conjetura de que la posicion semiclasica X(t) se puede relacionar físicamente con z(t), la posicion media del paquete de ondas cuántico definida arriba, i.e., cuando X(t) este acotada¹ en la Ec. (25), entonces la correspondiente z(t) también estara acotada² (al menos, como una condicion suficiente). Entonces, el criterio de Kroopnick toma la forma para n entero, donde U(X) es la parte estatica del potencial cuantico U(X, t) y f_n(X) son los coeficientes de Fourier de la fuerza periodica f(X,t+T) = f(X,t).

A continuacion dirigimos la atención hacia los casos de localización AC y AC+DC referidos arriba en el inciso (ii), que son los casos especiales del potencial lineal correspondiente a una fuerza periodica y homogénea f(X,t + T) = f(X,t) (en este caso, los coeficientes de Fourier f_n(X) = f_n también son independientes de X). Queremos verificar si sus correspondientes condiciones de localización cuántica conocidas para valores grandes de ω son consistentes con la condicion de Kroopnick. En el caso AC, U(X) = 0, entonces , por lo que la condicion de Kroopnick no se verifica (no hay localización); en el caso AC+DC, U(X) = , entonces , así que la condicion de Kroopnick se verifica (hay localización). Las correspondientes condiciones cuanticas de localización son las mismas cuando w es grande: en el caso AC, J₀(/ω) = 0 no se cumple y por lo tanto no hay localización; en el caso AC+DC, se cumple y por lo tanto hay localización. En vista de lo anterior, podríamos elaborar un argumento físico acerca de la transicion del régimen AC (con potencial U(X,t) = X cos ωt) al regimen AC+DC (con potencial U(X,t) = + X cos ωt) en terminos de una transición de un régimen de deslocalización a un régimen de localización. Podemos observar que dicha transicion consiste solamente de anadir el potencial al potencial AC. Sin embargo, tal adicion puede ser un asunto complicado en una red de estado solido. Veremos a continuación que en el dominio optico de un arreglo de guías de onda, dicha adicion se transforma en un procedimiento bastante practico.

De manera interesante, los resultados teoricos descritos arriba pueden encontrar un escenario experimental donde las predicciones serían confirmadas (o refutadas). Como se menciono al principio de este trabajo (seccion 1), existe una analogía formal entre el comportamiento de un electron moviéndose en una red de enlace fuerte bajo el efecto de campos electromagneticos especficos, y un paquete de ondas fotonico propagándose a lo largo de un arreglo de fibras opticas con perfiles de curvatura específicos. Así, los fenomenos dinámicos cuánticos para el electron en la red (en el dominio temporal) son "mapeados" a lo largo del eje del arreglo de fibras opticas (en el dominio espacial). Esto es posible despues de aplicar la transformación de Kramers-Henneberger a la "ecuación óptica de Schródinger" (Longhi et al. 2006), de lo que resulta

donde: z es la coordenada axial del arreglo optico, = x — x₀(z) es la coordenada transversal transformada, x es la coordenada transversal del arreglo donde las fibras opticas están distribuidas periodicamente con distancia de separación a, U_opt(x) = n_s — n(x), n(x) = n(x + a) es el índice de refraccion efectivo del arreglo óptico, n_s es el ındice de refracción del sustrato material que conforma cada fibra optica, x(0) describe el perfil de curvatura periodica del arreglo con periodo . Podemos reconocer en la Ec. (32) una ecuación tipo Schrödinger para una partícula de "masa" n_s moviendose en una red con "potencial periodico" U_opt () y sujeta a una "fuerza" externa equivale a la constante cuantica h. Ya que el "potencial" externo en la Ec. (32) es lineal en y ya que la coordenada espacial óptica z se relaciona con la variable temporal cuantica t, entonces los casos (i)-(iii) de localización descritos al inicio de esta sección se describen de manera equivalente por la Ec. (32) en el dominio espacial optico. Así, para un perfil de curvatura parabolico x₀ z² se obtuvo el efecto analogo a la oscilacion de Bloch (Lenz 1999); para un perfil de curvatura periodico se observo experimentalmente el efecto analogo a la localización dinamica AC (Longhi et al. 2006); y para un perfil de curvatura cúbico x₀ z³ el efecto analogo a la localización asintótica fue asimismo observado experimentalmente (Dreisow et al. 2011). 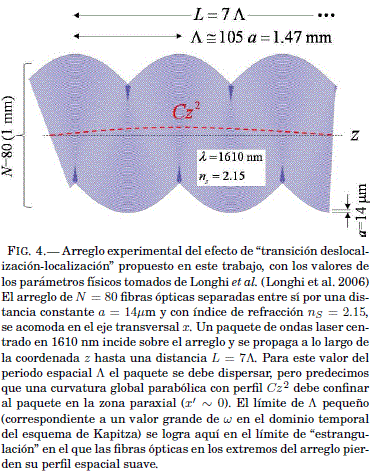Para el caso AC, esta claro que para un valor mayor de ω (i.e., un menor valor de ) la condicion de localización J₀(/ω) = 0 no se verifica y por lo tanto ocurre deslocalización, lo que a su vez implica que el paquete optico se dispersa a lo largo del eje transversal x. Sin embargo, si este arreglo optico se somete a una curvatura parabolica global, entonces se logra en el dominio optico el equivalente al caso de localización AC+DC pues la condición se verifica, así que el paquete optico no se dispersa y permanace acotado o confinado en torno a la regin paraxial del eje z. Este interesante efecto debería observarse como se indica en la Fig. 4, donde los valores de los parametros físicos se tomaron de Longhi et al. (Longhi et al. 2006). El procedimiento experimental sería entonces sencillo: el arreglo con un perfil periodico de curvatura donde no hay localización, se dobla con un perfil parabólico global Cz² (cualquier valor real de C sería, en principio, suficiente). El resultado entonces es que un paquete optico inicialmente disperso se localizaría en torno al eje z, logrando así la transicion de un régimen de deslocalización a uno de localización.

 

5. CONCLUSIONES

Aplicamos un metodo similar al de Kapitza (Kapitza 1951) que permitio obtener una expresión novedosa para la aceleracion efectiva independiente del tiempo de un electron en una red de enlace fuerte (Cf. Ec. (25)); sobre este electron actúan un campo electrico armónico rápidamente oscilante (ω → ∞) y un potencial estatico arbitrario. Los resultados que obtuvimos se pueden expresar en los terminos de un potencial efectivo simple (Cf. Ec. (26)) vía la introduccion de una masa efectiva de enlace fuerte m (Cf. Ec. (21)). En el límite del continuo definido por a → 0 y A → ∞, donde , el potencial efectivo U_eff(X) resulta ser (m* es la masa en el continuo)

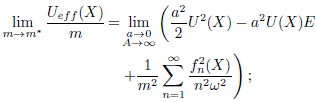
pero

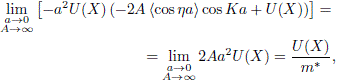
de tal forma que finalmente

que es el mismo resultado ya conocido en el continuo para el potencial efectivo U_eff(X) (Kapitza 1951; Bandyopadhyay & Dattagupta 2008; Rahav et al. 2003). Notablemente, la correccion dinámica de alta frecuencia del orden de O(ω^-2) en la Ec. (26) es formalmente similar a aquella asociada al límite del continuo, lo que se aplica asimismo a las aceleraciones respectivas. Podramos conjeturar si acaso esta similitud se mantiene (cuando ω → ∞) hasta el siguiente orden O(ω^-4) entre el resultado en el continuo y el resultado (aun desconocido) en la red. Finalmente, resulta interesante señalar que de la Ec. (17) para se puede demostrar la formula

ası, para a → 0 (en el continuo) la correccion de alta frecuencia para el potencial efectivo (para ω → ∞) es igual al valor medio de la energía cinetica del movimiento oscilatorio dado por . En resumen, la nueva formula dada en la Ec. (26) generaliza el celebre resultado de Kapitza para el pendulo invertido (Kapitza 1951) al caso de un electron de enlace fuerte. De esta forma, surgen aplicaciones interesantes (entre otras) al caso del oscilador armonico en la red (Longhi 2007; Gallinar & Chalbaud 1991) y al efecto de la oscilacion de Bloch (Bloch 1928), y asimismo se puede considerar como un primer paso conceptual importante en el estudio mas profundo (hasta el orden de O(ω^-4) de los efectos debidos a un campo forzador de alta frecuencia en la red. En particular, y motivados por la evidencia experimental reciente de localizacin dinamica y localización asintótica en arreglos de fibras ópticas, propusimos en la Sec. 4 un bosquejo de experimento que podría servir para verificar la prediccion teórica de que en un arreglo tal con un perfil de curvatura periodico (de periodo pequeño), un paquete de ondas fotonico se debería dispersar, pero si además se aplica a todo al arreglo una curvatura global parabolica, entonces se debería inhibir la dispersión del paquete y este permanecería confinado en la region paraxial del arreglo. Este experimento propuesto podría permitir ampliar el rango de aplicaciones de los resultados presentados aquı.

 

APENDICE

A. DEDUCCION DEL VALOR DEL TÉRMINO

Expandiendo hasta el orden de ω^-2 y promediando, se obtiene

donde esta dada por la Ec. (16). Así,

donde

lo que da

ya que f_n(X) = f_-n(X). Finalmente, la Ec. (A1) resulta en

 

B. DEDUCCION DEL VALOR DEL TÉRMINO

Sustituyendo por su valor dado en la Ec. (17) y f(X,t) dado en la Ec. (3), se obtiene

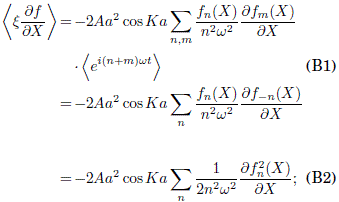
de lo que finalmente resulta (usando la Ec. (A3)):

Es conveniente señalar que la relación

se puede obtener asimismo de las Ecs. (12) y (15), las que al dividirse dan

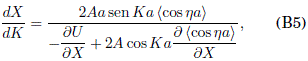
lo que conduce a la diferencial exacta d, y de aquí se tiene la Ec.(B4). Es interesante notar que en la Ec. (B4) el factor de estrechamiento de la banda coincide con la suma de los primeros dos terminos de la expansion de J₀(eεa/ω), donde J₀ es la funcion de Bessel de primer tipo y orden cero, i.e,

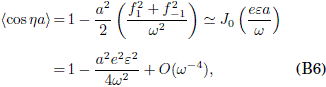
con f1(X) = f_-1(X) = -eε/2. Este resultado coincide hasta el orden de O(ω^-4), como debe ser, con el resultado exacto para la condicion de localización dinamica, i.e., J₀ (eεa/ω) = 0, lo que equivale a la anulacion del ancho de banda efectivo para el electrón de carga electrica (—e) en presencia de un campo electrico oscilante y homogéneo ε cos ωt.

 

C. CRITERIO DE KROOPNICK PARA MOVIMIENTO CONFINADO

En este apendice mostramos que, de acuerdo al teorema de Kroopnick (Kroopnick 1972), una condicion suficiente para que las soluciones X(t) de la Ec. (25) esten confinadas (o acotadas) en el límite t → ∞ , esta dada por para algun entero n. El referido teorema de Kroopnick establece que: para la ecuación

donde a(t) > 0 y b(X) son funciones continuas en los intervalos R⁺ = [0,∞) y R respectivamente, si a(t)≤ 0 (con t ≥ T) y , entonces todas las soluciones X(t) de la Ec. (C1) estan confinadas en el lımite t → ∞. En efecto, comparando la Ec. (25) con la Ec. (C1) se puede establecer a(t) = 1 y elegir

integrando b(X) resulta entonces

Así, la condicion de Kroopnick se cumple si para algun entero n. Para que este resultado corresponda a la aplicación del teorema de Kroopnick es necesario que: (para algun T tal que t ≥ T, por ejemplo, T = 0), donde a(t) es una funcion continua en R⁺ = [0,∞) y que b(X) en (C.2) sea continua en R. Ya que todas estas condiciones se cumplen, entonces la aplicación del teorema de Kroopnick es valida.

 

D. FRECUENCIAS CUASI-ARMONICAS DE OSCILACIONES PEQUEÑAS

Aplicamos la formula

donde es la frecuencia angular de las pequeñas oscilaciones cuasi-armonicas en torno al mínimo X₀ del potencial efectivo U_eff(X), a fin de obtener expresiones apropiadas para con las condiciones f_n(X) = 0 para todo entero n. En efecto, tenemos entonces que (Cf. Ec. (26)):

derivando la Ec. (D2) obtenemos

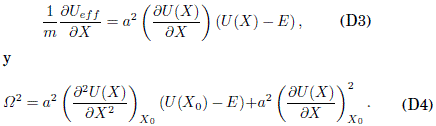
Si X₀ es un mínimo de U_eff(X), entonces obtenemos de las Ecs. (D3) y (D4) para :

cuando U(X₀) = E, o bien,

cuando . Para ilustrar la aplicación de las Ecs. (D5) y (D6) a un caso sencillo, consideremos la oscilacion de Bloch. En este caso U(X) = eε₀X para un electron de carga eletrica (—e) sujeto a un campo electrico estático y homogéneo ε₀. Ya que , entonces solo existe una frecuencia de la forma ₁ dada por la Ec. (D5). Luego, U_eff(X)/m esta dado por

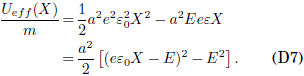
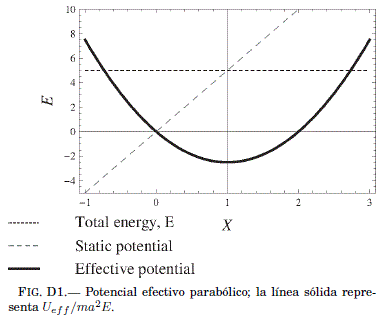
La Ec. (D7) corresponde a un pozo parabolico desplazado como se muestra en la Fig. D1. Obtenemos así la expresion independiente de la energa ₁ = aeε₀, que es la solucion exacta conocida para la oscilacion de Bloch, que en este caso es equivalente a un oscilador armonico simple.

 

NOTAS

¹ Se puede demostrar que si X(t) esta acotada, también lo está X(t), de tal forma que la region en el espacio fase para la evolución del sistema es finita.

² Notese que el valor cuadrático medio no tiene un equivalente semiclasico, lo que no impide formular la conjetura "acotamiento implica localización".

 

REFERENCIAS

Ashcroft N. & Mermin N. (1976), Solid State Physics (Holt, Rinehart Winston)         [ Links ]

Bandyopadhyay M. & Dattagupta S. (2008), Pramana J. Phys, 70, 381        [ Links ]

Bloch F. (1928), Z. Phys., 52, 555         [ Links ]

Buluta I. & Nori F. (2009), Science, 326, 108         [ Links ]

Dreisow F., Bahat-Treidel O., Welt D. & Szameit A. (2011), Opt. Lett., 36, 2065        [ Links ]

Dunlap D. H. & Kenkre V. M. (1986), Phys. Rev. B, 34, 3625         [ Links ]

Gallinar J. P. & Chalbaud E. (1991), Phys. Rev. B, 43, 2322         [ Links ]

Gallinar J. P. & Mattis D. C. (1985), J. Phys. A: Math. Gen., 18, 2583         [ Links ]

Garanovich I. L., Longhi S., Sukhorukova A. & Kivshar Y. (2012), Phys. Rep., 518, 1        [ Links ]

Georgescu I., Ashhab, S. & Nori F (2014), Rev. Mod. Phys., 86, 153         [ Links ]

Hartmann T., Keck F., Korsch H. J. & Mossmann S. (2004), New J. Phys., 6, 2         [ Links ]

Holthaus M. & Hone D. (1996), Phil. Mag. B, 74, 105        [ Links ]

Itin A. & Neishtadt A. (2014), Phys. Lett. A, 378, 822        [ Links ]

Kapitza R L. (1951), Collected papers of P. L. Kapitza (Pergamon Press, Oxford)        [ Links ]

Kroopnick A. (1972), Proc. Amer. Math. Soc., 34, 319         [ Links ]

Lenz G. (1999), Phys. Rev. Lett., 83, 963         [ Links ]

Longhi S. (2007), Phys. Rev. B, 76, 195119         [ Links ]

Longhi S., Marangoni M., Lobino M., Ramponi R. & Laporta R (2006) arXiv: quant-ph/0511132v2         [ Links ]

Marte M. & Stenholm S. (1997), Phys. Rev. A, 56, 2940         [ Links ]

Mattis D. C. (1986), Rev. Mod. Phys., 58, 361         [ Links ]

Mattis D. C. & Gallinar J. R (1984), Phys. Rev. Lett., 53, 1391         [ Links ]

Papp E. & Micu C. (2007), Low-dimensional nanoscale systems on discrete spaces (World Scientific Publishing Co. Pte. Ltd.)         [ Links ]

Rahav S., Gilary I. & Fishman S. (2003), Phys. Rev. A, 68, 013820         [ Links ]

Sanjines D. & Gallinar J. R (2001), Phys. Rev. B, 64, 054301         [ Links ]

Zhao X. G. (1991), Phys. Lett. A, 155, 299        [ Links ]