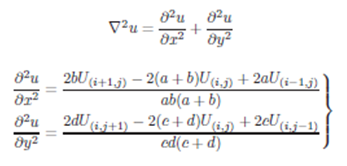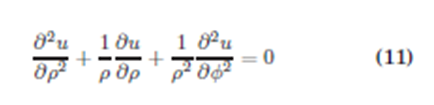Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.19 n.19 La Paz 2011
SOLUCIÓN DE ECUACIONES DIFERENCIALES PARCIALES
POR EL MÉTODO MONTE CARLO
SOLUTION OF PARTIAL DIFFERENTIAL EQUATIONS
BY THE MONTECARLO METHOD
Franz Suxo Mamanif
Instituto de Investigaciones Físicas, Carrera de Física
Universidad Mayor de San Andrés
c. 27 Cota-Cota, Campus Universitario, Casilla de Correos 8639
La Paz - Bolivia
Resumen
Se obtiene soluciones de ecuaciones diferenciales parciales (EDP) como ser la ecuación de Laplace para una región plana irregular y la ecuación del calor para una región plana circular y regular. Para ello se utiliza el método Monte Carlo a fin de simular paseos aleatorios que se realizan en regiones discretizadas que resultan de las EDP desarrolladas en diferencias finitas. La forma de discretización limita las direcciones de paso entre los nodos de la región y a la vez asigna probabilidades de transición entre dichos nodos. La idea de la metodología es que para determinar el valor de un nodo (i.e., la solución de un punto de la región discretizada) se lanza varias partículas desde el nodo y se las hace evolucionar de acuerdo a las probabilidades de transición hasta que choquen con el borde de la región discretizada, terminando así el paseo aleatorio; este borde constituye la condición de contorno de las EDP. Se presentan los resultados para la ecuación del calor en una placa delgada para seis instantes; los resultados de la ecuación de Laplace se presentan mediante dos situaciones físicas distintas: una membrana elástica delgada estacionaria y la distribución estacionaria de temperatura en una placa delgada.
Descriptores: técnicas computacionales y simulaciones - métodos de diferencias finitas - aplicaciones de métodos de Monte Carlo
Código(s) PACS: 02.70.-c, 02.70.Bf, 02.70.Uu
Abstract
We use the Monte Carlo method to obtain solutions of partial differential equations (PDE) such as the Laplace equation for a flat irregular region and the heat equation for a flat circular and regular region. With this method we simulate random walks in the discrete regions that result from the PDE developed as finite differences. The discretization process limits the possible directions between the region nodes and assigns them transition probabilities. To determine the value of the node (i.e., the solution for a point in the discretized region) we launch from the node several particles and let them evolve according to their probabilities until they reach the boundary region, which is the boundary condition for the PDE. We present the results of this method for the heat equation in a thin board for six different instants. For the Laplace equation the results correspond to two different physical systems: a stationary and elastic thin membrane and the stationary temperature distribution of a thin board.
Subject headings: computational techniques and simulations - finite-difference methods - applications of Monte Carlo methods
1 INTRODUCCIÓN
Problemas físicos de estado estacionario o problemas de evolución temporal son modelados a través de EDP's elípticas y parabólicas respectivamente, estas ecuaciones tienen una difícil solución por métodos exclusivamente analíticos cuando las condiciones de contorno e inicial no son sencillas, y en muchos casos no es posible encontrar una solución analítica, en especial problemas físicos reales que tienen regiones con una geometría no muy regular.
Existen varios métodos numéricos, como por ejemplo el Método ADI ([31995Press]) y el Método de Crank-Nicholson ([12000Kreyszig]) que son bastante flexibles para las condiciones iniciales y condiciones de contorno del problema, estos métodos consisten en desarrollar las EDP's en diferencias finitas y mediante operaciones matriciales obtener la solución. Y en relación a problemas que tienen regiones no tan regulares está el método de elementos finitos, en el que intervienen matrices y ecuaciones integrales 1.
La importancia de la aplicación del método Monte Carlo para resolver EDP's elípticas y parabólicas, radica en que se pueden asociar a un modelo probabilístico artificial de factores aleatorios, transformando el proceso de la solución del problema a simples conteos y promedios.
Un ejemplo sencillo para resolver la Ecuación de Laplace de una región plana cuadrada asociando un modelo probabilístico 2 se realiza con la siguiente analogía ([41972Sheid]). Un perro que está perdido en un laberinto cuadrado que tiene corredores interiores, en cada intersección escoge una dirección al azar y sigue hasta la siguiente intersección donde escoge de nuevo al azar y así sucesivamente, Cuál es la probabilidad que un perro que parta de una determinada intersección emerja eventualmente por el lado sur?. Según las condiciones de contorno el lado sur tiene el valor de 1 y los restantes lados el valor de 0, y estas intersecciones o probabilidades son la solución del problema.
Entonces, el propósito del presente trabajo es, mostrar una metodología para resolver EDP's a través de dos problemas específicos; la Ecuación de Laplace para una región plana irregular y la Ecuación del Calor para una región plana circular regular.
2 DISCRETIZACIÓN DE REGIONES
Al igual que los métodos númericos mencionados, la metodología a seguir se basa también en desarrollar las EDP's en Diferencias Finitas, con la finalidad de Discretizar la Región.
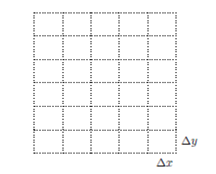
Si se considera el Laplaciano ∇2 u de una EDP para una Región Plana, su desarrollo en diferencias finitas debe tomar en cuenta la Geometría de la Región (forma de la Frontera).
2.1 Región Rectangular
El Laplaciano de una geometría rectangular se debe discretizar en Coordenadas Rectangulares. Entonces el desarrollo del Laplaciano ∇2 u en coordenadas rectangulares es:
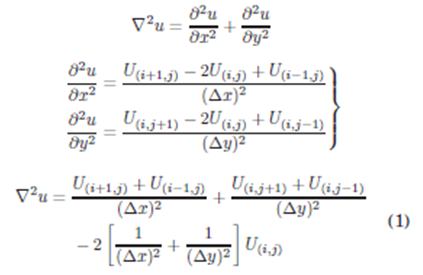
El Laplaciano de una geometría circular se debe discretizar en Coordenadas Polares.
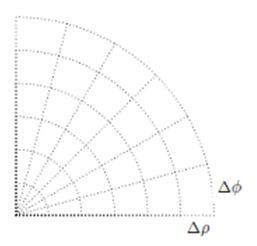
Si tenemos ρ = i∆ρ y ϕ = j∆ϕ entonces el desarrollo del Laplaciano ∇2 u en coordenadas polares es:

2.2 Región Circular
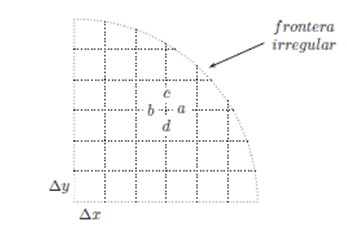
2.3 Región Irregular
Una geometría se dice que es irregular cuando las divisiones (∆'s) no son constantes. Este tipo de geometrías por simplicidad se deberían discretizan en Coordenadas Rectangulares (Si una región circular se desarrolla en coordenadas rectangulares, está región llega a ser una región irregular).
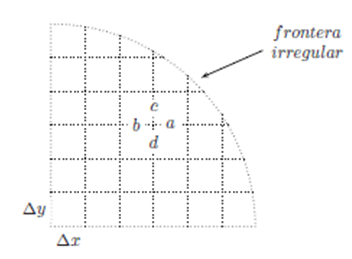
Las distancias a,b y c,d son constantes e iguales a ∆x y ∆y respectivamente, excepto cerca a la frontera irregular en el cual a < ∆x y c < ∆y. Por tanto, de manera general tenemos: a,b \leqslant ∆x y c,d \leqslant ∆y, entonces el desarrollo del Laplaciano ∇2 u de una geometría irregular es:
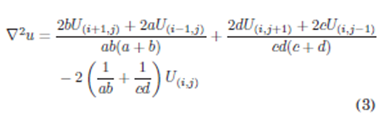
Para cualquier región en dos dimensiones sea irregular o no pero que esté desarrollada en coordenadas rectangulares, se utiliza la Ec. (3) de manera general (Véase que la Ec. (1) es un caso especial de la Ec. (3)).
3 PROBABLIDADES DE TRANSICIÓN
Al desarrollar las EDP's en Diferencias Finitas, además de Discretizar la Región, también se pueden obtener Probabilidades de Transición que se tienen entre los nodos de la región.
Para tal objetivo, partimos de la Ec. (4) que es una EDP homogénea que no contiene el término de la función sin derivar f(x,y,z,...), sin embargo aún esta ecuación es bastante general al cual se aplica el siguiente teorema que se propone en el presente trabajo.
En el desarrollo en diferencias finitas de cualquier ecuación diferencial parcial donde todos los términos poseen derivadas de primer orden o mayor, puede afirmarse que, el coeficiente del término en el cual se desarrolla la serie es igual al negativo de la suma de coeficientes que ocupan los términos vecinos. Entonces, despejando el término en el que se desarrolla la serie, los coeficientes resultantes de los términos vecinos pueden ser tratables como probabilidades.
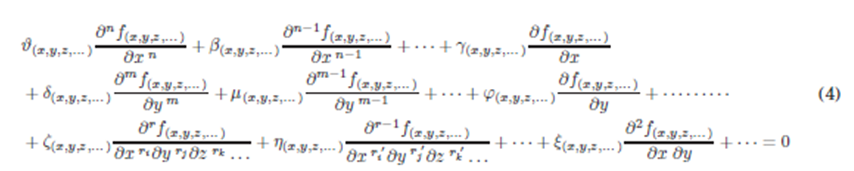
[Demostración.] De la fórmula de interpolación con diferencias hacia adelante de Gregory-Newton ([12000Kreyszig]):
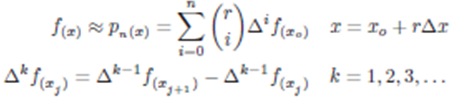
Se obtienen las Ecs. (5) que son las derivadas n-ésimas de la función f(x,y,z,...), donde estas ecuaciones llevan una sumatoria de coeficientes binomiales por cada variable que es derivado.
Estas derivadas n-ésimas pueden descomponerse aislando un término determinado de la(s) sumatoria(s), en este caso; cuando (i=a) en la primera y cuando (i=a ∧ j=b ∧ k=c ∧ ) en la segunda. Resultando de esta manera las Ecs. (6).
Entonces, al desarrollar alrededor de (xa,yb, ) la Ec. (4) en Diferencias Finitas utilizando las Ecs. (6) se obtiene la Ec. (7), donde la función en el punto de desarrollo está despejada (a modo de ilustración solo se reemplazaron dos términos representativos pero generales; la derivada n-ésima de una variable y la derivada r-ésima cruzada).
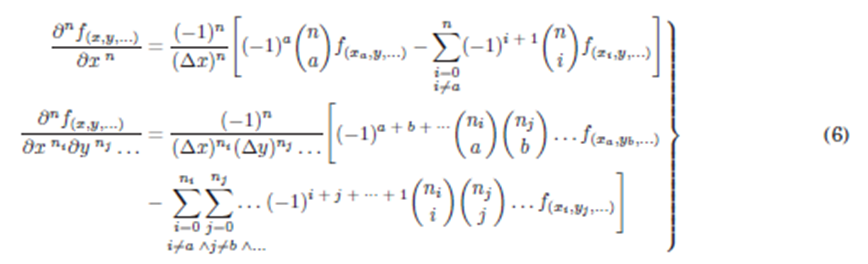
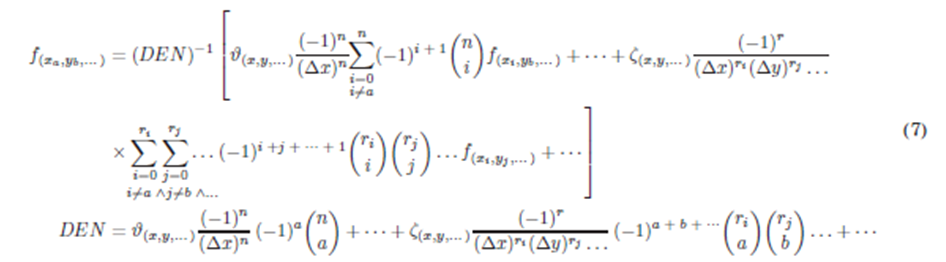
Por tanto, haciendo uso de la siguiente propiedad de coeficientes binomiales ([51986Spiegel]):
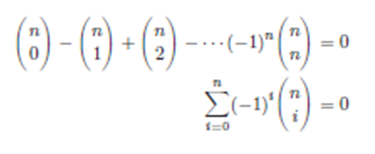
Se puede aislar y despejar el coeficiente cuando (i=a), y de manera semejante cuando existe una composición de coeficientes binomiales, es decir cuando (i=a ∧ j=b ∧ k=c ∧
). Entonces:
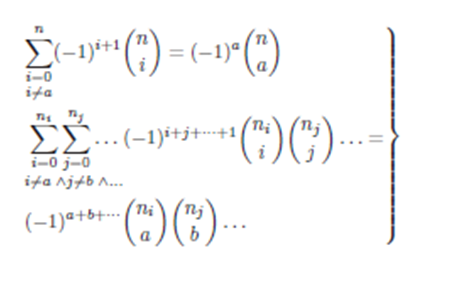
Finalmente, utilizando estas dos últimas igualdades al sumar todos los coeficientes de los términos f(xi,yj, ) del numerador (términos vecinos) de la Ec. (7), resulta que, la sumatoria es igual al denominador del mismo 3.
Entonces, al ser distribuido el denominador a todos los términos f(xi,yj, ), la sumatoria de los coeficientes resultantes es igual a la unidad. Con tal resultado queda demostrado el Teorema propuesto aplicado a la Ec. (4).
3.1 Normalización de Coeficientes
Los coeficientes de la Ec. (7) cuando se reparte el denominador pueden tener valores; positivos, negativos ó ceros. Pero la sumatoria de dichos coeficientes es igual a la unidad. Véase el siguiente esquema.
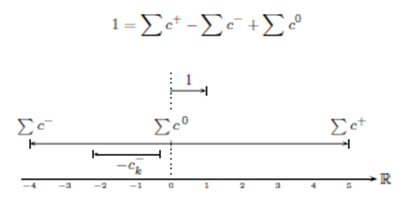
Pero al cambiar el signo de los coeficientes negativos a positivo se obtiene el siguiente esquema.

En el cual la longitud de un determinado coeficiente ck (sea positivo, negativo o cero) y la longitud total no cambia. Por tanto, se puede normalizar 4 los coeficientes cambiándole el signo a los negativos y dividiendo a cada coeficiente por la longitud total. Entonces, estos coeficientes resultantes de la normalización pueden ser tratables como Probabilidades.
4 EL MÉTODO MONTE CARLO
La Región Discretizada más las Direcciones y Probabilidades de Transición obtenidas mediante el desarrollo por Diferencias Finitas, nos permite realizar Paseos Aleatorios en dicha región. Además es necesario la generación de Numeros Aleatorios en toda la trayectoria del paseo aleatorio, siendo este el fundamento del método Monte Carlo.
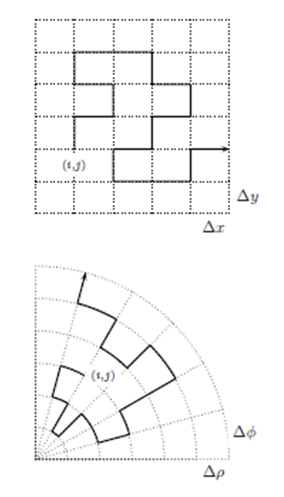
El algoritmo del método Monte Carlo para aproximar u consiste en lo siguiente: Para conocer el valor de solución u en un nodo (i,j) de la región, se larga una partícula desde ese nodo y se la hace evolucionar de acuerdo a las direcciones y probabilidades de transición calculadas, hasta que choca con la frontera de la región 5, almacenándose el valor del dato de frontera en ese punto. Se repite este procedimiento para una gran cantidad de partículas, y se estima el valor de u(i,j) como el promedio de esos valores. Graficamente se muestra a continuación paseos aleatorios en regiones rectangulares y circulares respectivamente.
4.1 Condiciones de Frontera
Si una partícula simulada llega a una frontera que tiene Condiciones de Contorno de Dirichlet o Condiciones Iniciales, termina el paseo aleatorio de la misma. Pero no sucede lo mismo cuando la partícula llega a una frontera que tiene Condiciones de Contorno de Neumann, en este caso se debe desarrollar el gradiente en diferencias finitas centrada en la frontera.
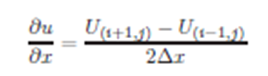
Donde U(i+1,j) está fuera de la región. Si el gradiente es igual a cero entonces se tiene U(i+1,j)=U(i−1,j) que puede ser reemplazado en la ecuación que lleva las probabilidades de transición para generar una nueva ecuación, que se utiliza cuando la partícula llega a esta frontera.
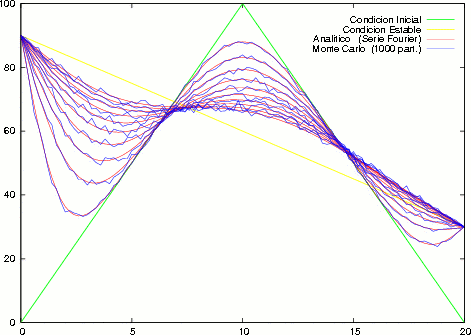
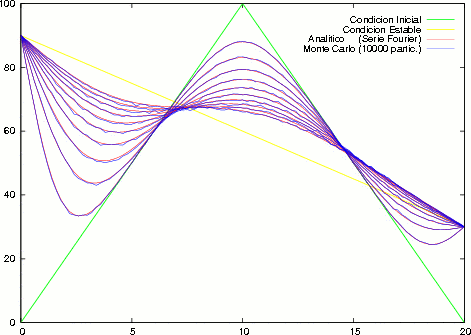
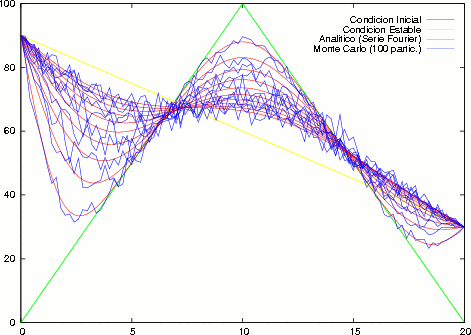
Figure 1: Solución de la Ecuación del Calor Analítica y por Monte Carlo
Se compara soluciones obtenidas por este método con soluciones analíticas de problemas que tienen condiciones de Dirichlet, Neumann e Iniciales.
-
En la Fig. (1) se muestra la solución de la Ecuación del Calor unidimensional para diez instantes de tiempo.
-
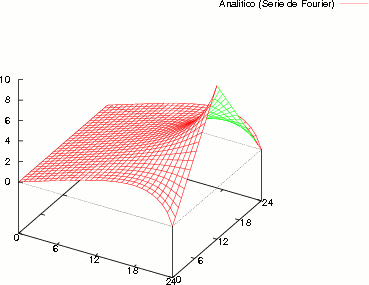
En la Fig. (2) se muestra la solución de la Ecuación de Laplace bidimensional.
Comparando la solución Analítica con el Método de Montecarlo para 100, 1000 y 10000 particulas en ambos casos.
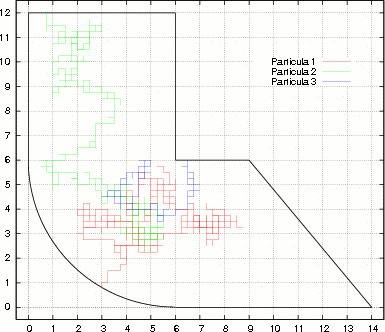
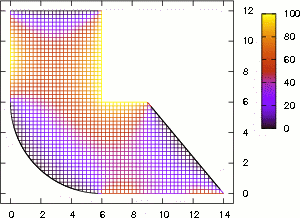
Se resuelve la Ecuación de Laplace, Ec. (8), en coordenadas rectangulares para una región irregular en el plano, ver Fig. (3).
![]()
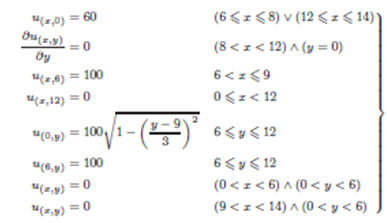
Para desarrollar la Ecuación de Laplace en diferencias finitas, se reemplaza el Laplaciano en coordenadas rectangulares para una región irregular, que es la Ec. (3), en la Ec. (8).
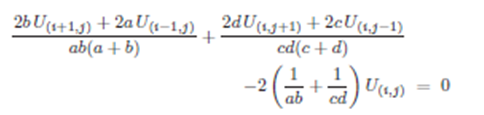
Luego, según la definición se procede a despejar el término central U(i,j).
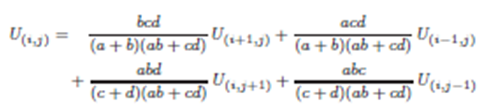
En el cual se tiene, cuatro direcciones de transición: U(i+1,j), U(i−1,j), U(i,j+1) y U(i,j−1), entonces el paseo aleatorio se realiza en el plano, donde las condiciones de contorno son los bordes de la región plana, ver Fig. (3). Y las probabilidades de transición a esas direcciones son los valores de sus respectivos coeficientes.
Los resultados obtenidos se presentan gráficamente para dos situaciones físicas distintas:
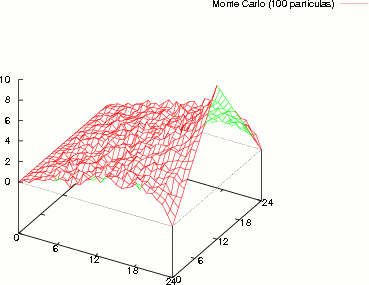
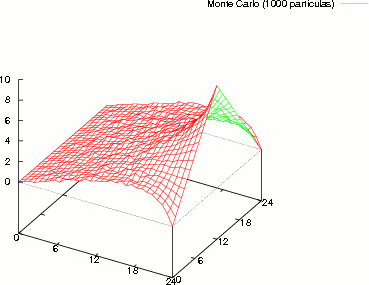
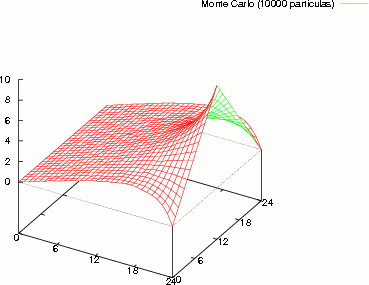
Figure 2: Solución de la Ecuación de Laplace Analítica y por Monte Carlo
Figure 3: Dimensiones espaciales de la región plana irregular. También se muestran tres paseos aleatorios
Figure 4: Se muestra la solución de la Ecuación de Laplace para una Membrana elástica delgada estacionaria
Figure 5: Se muestra la solución de la Ecuación de Laplace para la Temperatura estacionaria en una placa delgada
-
Una membrana elástica delgada estacionaria. Que es deformada en los bordes según las condiciones de contorno dadas, ver Fig. (4).
-
La temperatura estacionaria en una placa delgada. Los bordes están a temperaturas según las condiciones de contorno, ver Fig. (5).
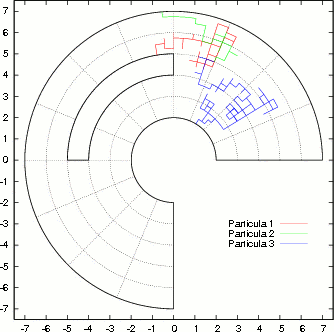
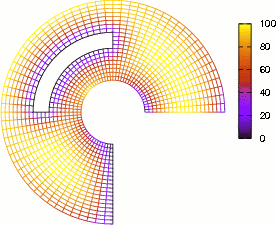
4. Figure 6: Dimensiones espaciales de la región plana circular regular. También se muestran tres paseos aleatorios
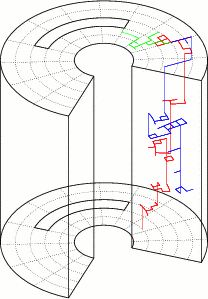
6. Figure 7: Se muestran tres paseos aleatorios realizados en la región discretizada del problema (volumen cilíndrico).
6 LA ECUACIÓN DEL CALOR
Se resuelve la Ecuación del Calor, Ec. (9), en coordenadas polares para una región circular regular en el plano, ver Fig. (6).
Entonces u=u(ρ,ϕ,t). La condición Inicial más las condiciones de contorno de Dirichlet y Neumann que tiene el problema se listan a continuación.
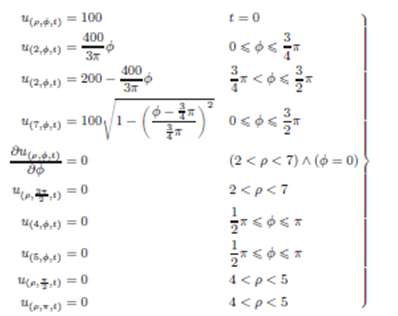
La Ec. (2) es el desarrollo de la parte espacial de la Ecuación del Calor, y de la parte temporal, es la Ec.(10).
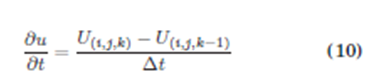
Por tanto, reemplazando la Ec. (2) y Ec.(10) en la Ec.(9), se obtiene el desarrollo en diferencias finitas de la Ecuación del Calor.
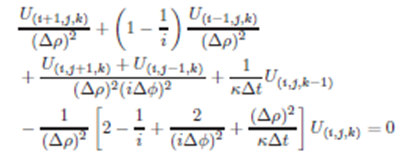
Realizando los siguientes cambios de variable para una mejor manipulación:
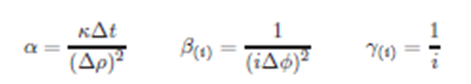
Se procede a despejar el término central U(i,j,k) según la definición.
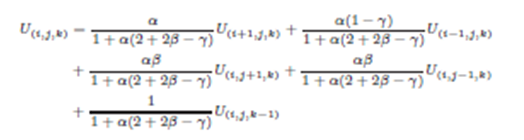
a)
b)
c)
d)
e)
f)
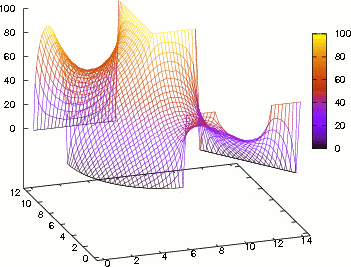
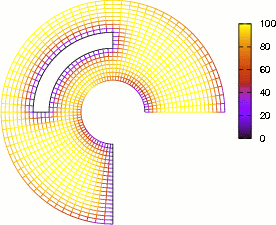
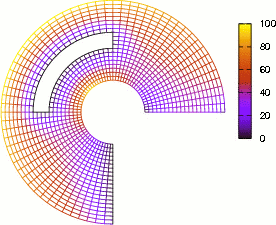
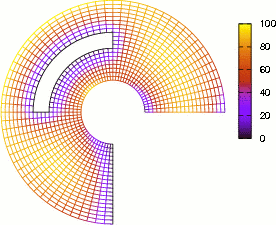
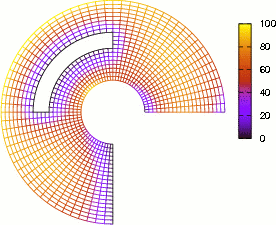
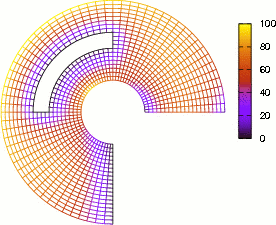
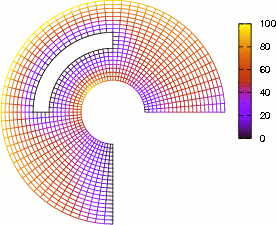
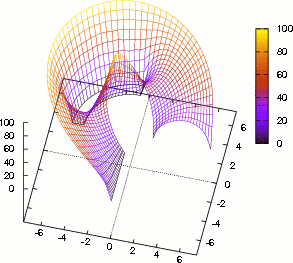
Figure 8: Se muestra la solución de la Ecuación del Calor de una región plana circular regular para seis instantes de tiempo consecutivamente, posteriores a la condición inicial. La paleta de colores muestra el rango de temperatura de 0 a 100.
a)
b)
Figure 9: Solución de la Ecuación de Laplace en coordenadas polares para una región plana circular regular. El inciso a) muestra la temperatura estacionaria en una placa delgada. El inciso b) muestra a una membrana elástica delgada estacionaria.
En el cual se tiene, cinco direcciones de transición, cuatro espaciales: U(i+1,j,k), U(i−1,j,k), U(i,j+1,k), U(i,j−1,k) y una temporal U(i,j,k−1). La dirección temporal hace que el paseo aleatorio se realice en un volumen cilíndrico, ver Fig. (7), donde las superficies laterales son las condiciones de contorno y la superficie inferior es la condición inicial.Y las probabilidades de transición a esas direcciones son los valores de sus respectivos coeficientes.
6.1 Resultados
Los resultados obtenidos son presentados gráficamente mediante seis instantes de tiempo consecutivos, posteriores a la condición inicial, ver Fig. (8). El primer inciso de la gráfica muestra que predominan las Condiciones Iniciales en un comienzo, mientras que el último inciso, muestra a las Condiciones de Contorno como predominantes.
Finalmente, en un tiempo relativamente largo, solo sobrevive la información de las condiciones de contorno y la información de las condiciones iniciales desaparece totalmente. Entonces los resultados de la Ecuación del Calor deben desembocar en los resultados de la Ecuación de Laplace al transcurrir el tiempo.
Entonces para fines comparativos, se obtiene la solución de la Ec. (11), que es la Ecuación de Laplace para este problema, cuyos resultados se muestran en la Fig. (9).
Observando la Fig. (8) y la Fig. (9), se puede comprobar, que en un tiempo relativamente largo, el proceso de difusión del calor se detiene llegando a un estado estacionario.
7 CONCLUSIONES
El método Monte Carlo aplicado para resolver EDP's es destinado especialmente para las ecuaciones Elípticas y Parabólicas, porque estas modelan fenómenos que inducen un proceso de achatamiento o promediado, donde las ecuaciones de Laplace y del Calor abordados en este trabajo son un buen ejemplo de este tipo de EDP's.
La eficacia del método se comprueba al comparar resultados en problemas que tienen soluciones analíticas, obteniéndose buena aproximación a medida que se aumenta el numero de partículas en las simulaciones. Por tanto se aplica el método con la seguridad de obtener buenos resultados en problemas que tienen regiones no muy simétricas los cuales no tienen una solución analítica.
Por otra parte, en este trabajo se resolvieron problemas que tienen dos dimensiones espaciales, tanto en la Ecuación de Laplace como en la Ecuación del Calor. Pero el método se puede extender a tres dimensiones espaciales sin ninguna dificultad en ambos casos, porque lo único que cambia es, el aumento en una dimensión de la región discretizada en el cual se realiza el paseo aleatorio.
References
1.- Kreyszig, E. 2000, Matemáticas Avanzadas para Ingeniería, Vol. II, Métodos Numéricos para Ecuaciones Diferenciales Parciales, 551,427 [ Links ]
2.- Perez, V. 2008, Métodos Matemáticos, Diferencias Finitas para Ecuaciones de Evolución, 147, 148, 160 [ Links ]
3.- Press, R. 1995, Numerical Recipes in C, Partial Differential Equations, 831, 832 [ Links ]
4.- Sheid, F. 1972, Análisis Numérico, Sistemas Lineales, La Iteración de Gauss-Seidel y la Super-Relajación, Los Métodos de Monte Carlo, 340, 404 [ Links ]
5.- Spiegel, M. 1986, Manual de Fórmulas y Tablas Matemáticas, La Fórmula del Binomio y Coeficientes Binomiales, 4 [ Links ]
Recibido 26 de agosto de 2011; aceptado 5 de septiembre de 2011