Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Revista Boliviana de Física
versión On-line ISSN 1562-3823
Revista Boliviana de Física v.13 n.13 La Paz 2007
ARTÍCULO ORIGINAL
ESTUDIO DE DOS CIRCUITOS CAÓTICOS
G. Conde S., G. M. Ramírez A.
Carrera de FísicaU.M.S.A.
RESUMEN
Se describe el proceso para caracterizar numéricamente un circuito autónomo tipo Chua (compuesto por dos capacitores, una bobina, una resistencia y el diodo de Chua), seguido de una verificación experimental y una comparación cualitativa con un circuito no autónomo R-L-diodo. Manteniendo el parámetro de control = C2/C1 fijo y aumentando los valores β= R2C2/L y γ= RroC2/L, según el modelo de Chua, el sistema presenta estados en el siguiente orden: divergencia (inestabilidad), caos (con ventanas periódicas) y finalmente periodicidad con tendencia a un punto fijo. En el laboratorio, el comportamiento es similar, sólo que en vez de divergencia se tiene un ciclo límite de primer orden, luego la región caótica a veces contiene ventanas periódicas y finalmente se presentan ciclos límite de segundo y primer orden terminando en un punto fijo. Experimentalmente, el parámetro de control fue la resistencia y los componentes más importantes para obtener caos fueron: C1 = 10 pF y L=1 mH (ro = 21.4 9); C2 podía tomar valores desde 1.5 nF hasta 47 nF, y R desde O Sl hasta 2 1(
Descriptores: Circuitos Electrónicos, Caos, Atractores Extraños.
1. INTRODUCCIÓN
El estudio de los fenómenos no lineales en nuestro medio ha tornado un aspecto teórico en su mayoría, y poco a poco ha crecido el interés por servirse de sus herramientas y aplicarlas en una variedad de áreas. En especial, los atractores extraños son considerados como abstracciones que solamente se observan en libros o en simulaciones y el caos, da la impresión de presentarse solamente en sistemas muy grandes corno los sociales o biológicos. Sin embargo, estos fenómenos pueden observarse en sistemas de fácil construcción y manejo. Una forma de llegar a este propósito es mediante la electrónica, que desde principios del siglo pasado, ha reportado circuitos con comportamientos "inusuales" y desde entonces se han realizado varios estudios rigurosos e investigaciones, desarrollándose aplicaciones en la tecnología de comunicaciones y proponiéndose nuevas aplicaciones incluso en la medicina. Existen varios circuitos electrónicos que al contener un elemento no lineal presentan comportamientos irregulares, uno de ellos es el circuito autónomo tipo Chua, planteado por el ingeniero electrónico chino León Chua en 1971. Si bien fue planteado en ese año, la primera evidencia de caos en este circuito fue en 1983 por simulación, realizado por T. Matsumoto [ 1] y la primera evidencia experimental de caos fue realizado por Zhong y Ayron en 1984 [2], posteriormente, se presentó un trabajo con pruebas rigurosas de la familia entera de atractores caóticos de este circuito [3]. Finalmente, el circuito ha formado parte de la base para investigaciones en sincronización caótica y otras variedades incluyendo aplicaciones en la encriptación de señales [4], [5], [6].
Por otra parte, un circuito RLC con un capacitor variable como elemento no lineal y una fuente de voltaje sinusoidal fue descrito por Paul Linsay en 1981, encontrando que el sistema experimental daba resultados concordantes con la teoría de sistemas no lineales [7].
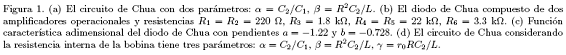
Desde entonces se realizaron modificaciones y estudios de este sistema, buscando las verdaderas causas de la no linealidaid, mas aplicaciones específicas aún no se han encontrando.
Debido al interés por estudiar y observar fenómenos no lineales como el caos y la ruta que nos lleva hacia él, se pretende caracterizar numéricamente el circuito tipo Chua y realizar observaciones en el osciloscopio a manera de una verificación experimental. Por otro lado, se pretende realizar una comparación cualitativa, con un circuito no autónomo compuesto por una fuente de voltaje alterna, una resistencia, una bobina y un diodo normal.
2. EL CIRCUITO TIPO CHUA
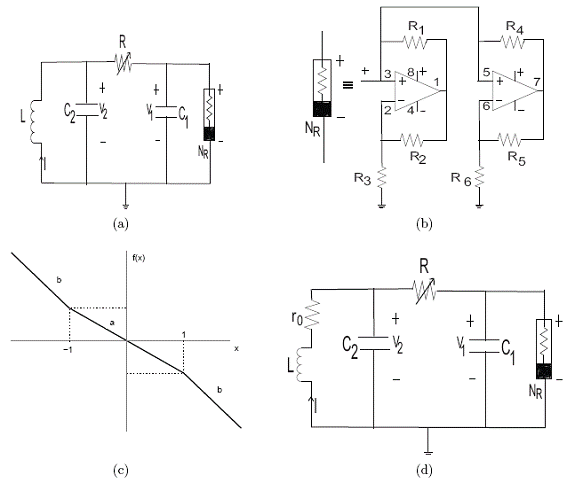
Este circuito se caracteriza principalmente por dos aspectos: primero, es autónomo, es decir, no está alimentado por fuentes de corriente alterna y segundo, está compuesto por dos partes: una parte que presenta un comportamiento típico de un oscilador amortiguado(dos condensadores, una resistencia y una bobina) y la otra parte que constituye el único elemento no lineal denominado diodo de Chua. Este elemento causante de la no linealidad actúa como la fuente de energía de todo el circuito, se ocupa de retroalimentarlo y lo mantiene oscilando (ver figura la).
El circuito tipo Chua se describe mediante el siguiente sistema de ecuaciones diferenciales:
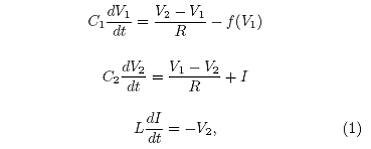
donde la función del diodo de Chua:
f (V1 ) = mbV1 + ½(ma mь)[|V1 +B|- |V1 -B|] tiene pendientes negativas ma, mb y un punto de ruptura dependiente del voltaje de saturación del amplificador operacional B. Estas expresiones están en función de los valores de componentes en el circuito del modo siguiente:
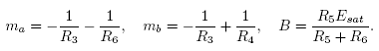
El diodo de Chua, básicamente, contiene dos amplificadores operacionales con un juego de seis resistencias, el
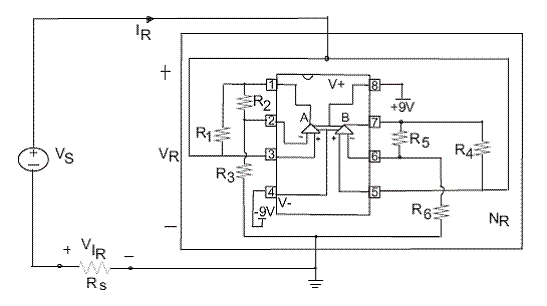
Figura 2. Arreglo experimental para medir la curva característica del diodo de Chua. Se aplica un voltaje Vs de una función sinusoidal al circuito en serie compuesto por la resistencia sensible R, y el diodo NR. El TL082 fue alimentado por ± 15 V.
arreglo se observa en la figura lb. Los valores adecuados para presentar no linealida..d fueron determinados en [8] y son una variación de los valores propuestos inicialmente por J. M. Kennedy [9]. La función f(V1) de este diodo se caracteriza por una curva V-I no lineal compuesta por tres rectas con pendiente negativa y un arreglo experimental para su obtención se sugiere en [10].
El modelo de Chua se presenta en forma adimensional introduciendo los términos siguientes:
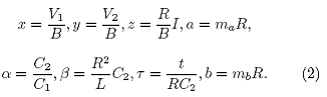
Entonces, se tiene un sistema de tres ecuaciones diferenciales que en principio depende de dos parámetros y β. Pero, considerando la resistencia intrínseca ro de la bobina (ver figura 1d), se introduce un tercer parámetro ![]() al sistema de ecuaciones (3).
al sistema de ecuaciones (3).
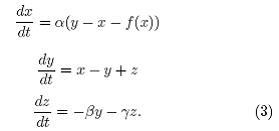
La forma adimensional de la función del diodo de Chua es f (x) = bx + ½(a – b)(|x + 1|– |x –1|), la cual se muestra en la figura lc. Se utilizaron los valores sugeridos para a = –1,22 y b = –0,728 [8].
2.1. Obtención Experimental de
Se construyó el arreglo experimental que se observa en
La resistencia sensible Rs fue utilizada para medir la corriente IR que fluye por el diodo cuando se aplica un voltaje VR a sus terminales. Por comodidad se escogió el valor de Rs = 1 k9 pues VIs = –IR e IR está dado en [mA].
Se obtuvo la curva característica del diodo aplicando el voltaje de fuente Vs, conectando Vi al canal Y del osciloscopio y VR al canal X y observando en el modo X-Y. Como sabemos que ![]() , entonces, para obtener la curva exacta:
, entonces, para obtener la curva exacta: ![]() , se invirtió la entrada de Y.
, se invirtió la entrada de Y.
Los resultados obtenidos se muestran en
3. ESTUDIO CUALITATIVO DEL CIRCUITO
3.1. Atractores periódicos y caóticos
El sistema no lineal de Chua, presenta cambios de estado según varíe el conjunto de parámetros {, β, γ} y las condiciones iniciales {xo, Yo, zo}. A las representaciones gráficas de estos resultados en el espacio de fases las llamamos trayectorias y se pueden tener los siguientes casos:

Figura 3. Curvas características I vs. V del diodo de Chua. Se observa que la fuente de 10 V es muy ruidosa.
· Puntos fijos. Es el caso más sencillo que representa un estado estacionario del sistema. En la serie temporal se presenta una función continua.
· Ciclos límite. O puntos periódicos representan un estado oscilatorio del sistema y todas las trayectorias pasan una y otra vez por su propio valor inicial trazando una curva cerrada. En la serie temporal se observa una función periódica.
· Casi-periodicidades. Representan la superposición de estados oscilatorios con periodos distintos y el espacio más apropiado para trazar estas trayectorias es el toroide. En la serie temporal se presenta como una función modulada.
Hasta este punto los casos vistos se denominan periodicidades.
A tractores Extraños. Este es otro caso posible que corresponde a estados aperiódicos. Una de las características de un atractor extraño es que en el espacio de fases existe un proceso llamado "stretching and folding" (estirar y doblar), lo que significa que en las trayectorias se produce una especie de estiramiento y luego un plegado sin que ellas se intersecten. Los atractores extraños son las representaciones en el espacio de fases de sistemas caóticos.
De este modo, un sistema podría sufrir cambios de acuerdo a los parámetros que se utilicen. Estos cambios cualitativos se denominan bifurcaciones y los puntos donde ocurren estos cambios se denominan puntos de bifurcación. Estas bifurcaciones podrían desembocar en comportamientos caóticos, los cuales se definen como comportamientos irregulares de un sistema determinista muy sensible a las condiciones iniciales [11].
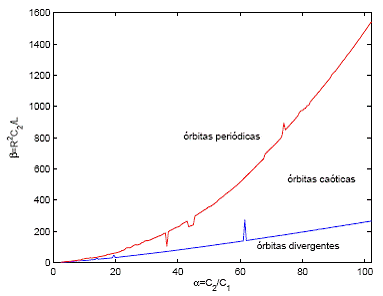
Figura 4. Caracterización del circuito tipo Chua con dos parámetros.
3.2. Metodología y Resultados para
Se comenzó resolviendo numéricamente el sistema de Chua mediante un programa en Matlab, en el cual los valores a ser introducidos fueron las condiciones iniciales: [xo, yo, zo] = [0.1, 0.15, 0.01], el tiempo de integración: t = 1500, los valores de las pendientes: a = 1,22, b = 0,728 y en principio, los parámetros: y β, los cuales son variados.
Se realizó un estudio cualitativo del sistema, esto significa que se observaron las trayectorias en el espacio de fases. Lo primero que se hizo fue elegir un valor de y variar el valor de β. De este modo se encontraron los límites de β, observando si la representación en el espacio de fases era un atractor extraño para el a elegido. Luego,
TABLA 1
Límites caóticos para la caracterización del sistema de Chua con dos parámetros
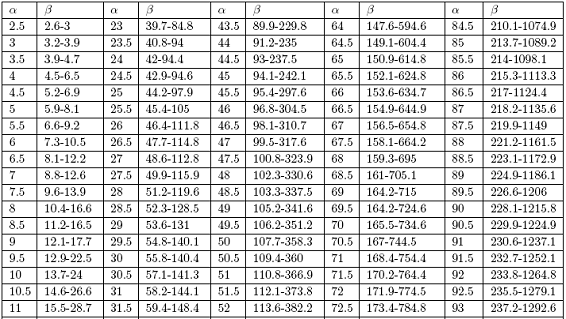
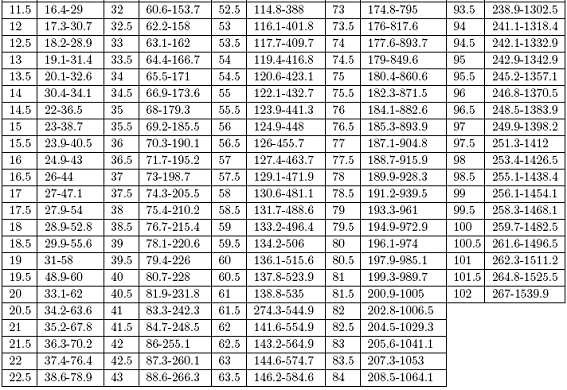
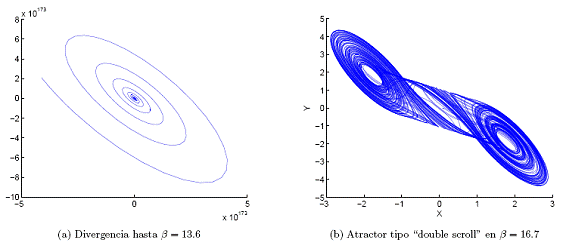
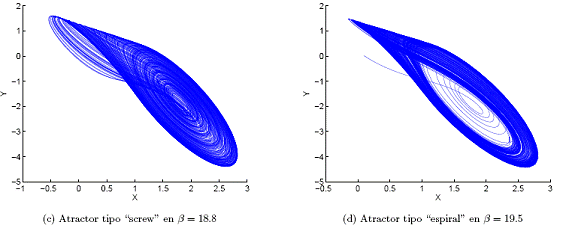
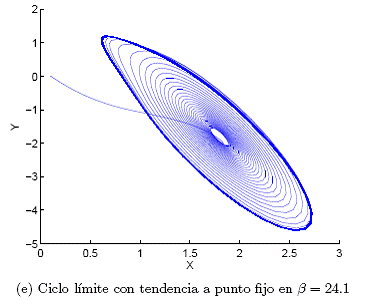
Figura 5. Para a = .10, se tiene la bifurcación según el parámetro /3. Dentro la región caótica j.3 E [13.7, 24] se encuentran variedades de atractores extraños.
TABLA 2
Límites caóticos para la caracterización del sistema de Chua con tres parámetros.
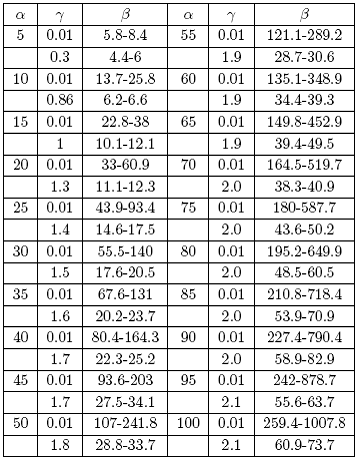
se cambió el valor de a y se encontró su correspondiente intervalo de 0. Para todas las ejecuciones se utilizó el mismo tiempo de integración y las mismas condiciones iniciales.
Con los datos de la tabla 1 se obtuvieron las regiones de caos y periodicidades representadas en
Se observó que a partir de = 2.5, se encuentran atractores caóticos en un amplio rango de β. Cuando este parámetro aumenta de valor, el sistema en general presenta atractores en el orden siguiente: divergencia en el modelo, lo que implica un estado inestable. Luego, el sistema presenta atractores caóticos, y finalmente atractores periódicos (con tendencia a un punto fijo).
Ha sido interesante notar que también existe un rango de condiciones iniciales para el cual se tiene un atractor. Este rango va creciendo a medida que a aumenta. La condición inicial para xo es la que tenía el rango más amplio, luego yo y finalmente zo tiene un rango más restringido. Por ejemplo, para = 10 y β = 13.7, se obtiene un atractor extraño y su rango de condiciones iniciales va desde [0.1, 0.15, 0.011 hasta [1.3, 0.19, 0.01]. Quizás esto no es tan sorprendente debido a que es la característica principal de un sistema caótico.
Posteriormente, se observó que la región de caos va creciendo con y β. En la tabla 1 se presentan datos hasta = 102, esto no significa que ahí termina la región, de hecho el rango continúa creciendo. Sin embargo determinar los límites hasta este valor fue suficiente para los propósitos de este trabajo.
Es importante mencionar que cada valor límite de β para todo , ha sido verificado con el exponente de Lyapunov. Como se verá más adelante, el exponente de Lyapunov es una herramienta cuantitativa que ayuda a verificar la presencia de caos en un sistema.
Dentro de la región caótica, existe una variedad de formas de atractores extraños que, en estudios previos, cada uno de ellos ha sido bautizado con algún nombre, como por ejemplo: "double scroll" (Fig. 5(b)), "screw type" (Fig. 5(c)), "spiral" (Fig. 5(d)). Como ya se había mencionado, cuando fi aumenta, antes de ingresar a la región caótica, se tiene una divergencia y luego una tendencia a un ciclo límite y finalmente a un punto fijo (ver Figs. 5(a) y (e)). Estas regiones no están determinadas en detalle, esto significa que dentro de la región caótica es posible encontrar ventanas periódicas y dentro de la regi´on peri´odica es posible encontrar atractores casiperiódicos.
3.3. Metodología y Resultados para
Hasta cierto punto los pasos fueron los mismos que en la anterior caracterización.
Se empezó resolviendo numéricamente el sistema de Chua mediante el mismo programa en Matlab, excepto que esta vez se consideró un tercer parámetro γ.
Al principio, el estudio realizado fue cualitativo. Primero, se eligió un para que quede fijo, luego se buscó el rango de β para un γ mínimo y lo mismo se buscó para un γ máximo. Luego, se escogió otro valor de a y se encontraron sus correspondientes intervalos de β y γ. En todos los casos se utilizó el mismo tiempo de integración t, las mismas condiciones iniciales (xo, yo, zo) al igual que las pendientes a y b.
La caracterización de la región caótica, se presenta en la tabla 2, en el cual se observan los valores límites de β para el máximo y mínimo valor de γ correspondiente a cada valor de . La región caótica delimitada por los tres parámetros se muestra en
4. ESTUDIO CUANTITATIVO DEL CIRCUITO
4.1. El Exponente de Lyapunov
El exponente de Lyapunov es una herramienta muy útil para determinar si un sistema dinámico es o no caótico.
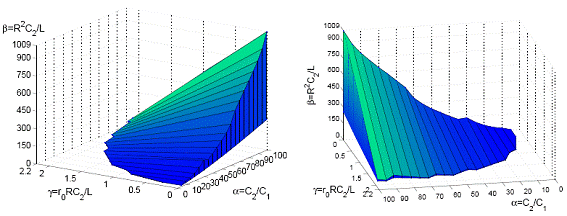
Figura 6. Caracterización del circuito tipo Chua con tres parámetros. Se muestran dos vistas de la región caótica. Esta región podría contener huecos debido a las ventanas periódicas.
Si al sistema de Chua se le asigna una condición inicial [x(0), y(0), z(0)], la integración numérica proporciona una serie temporal para cada una de las coordenadas. Si la misma condición inicial es modificada ligeramente, entonces se tiene una serie temporal que al principio recorre la misma trayectoria anterior pero después de un tiempo ésta se va separando exponencialmente. Este fenómeno es una característica de un sistema caótico ya que el comportamiento de las trayectorias depende de las condiciones iniciales y precisamente explica porqué estos sistemas son difíciles de predecir a largo plazo (ver Fig. 7).
El exponente de Lyapunov se representa por λ y es una cuantificación del crecimiento exponencial de la distancia entre dos puntos de dos series temporales con condiciones iniciales ligeramente distintas de un sistema dinámico determinista. El número de exponentes de Lyapunov depende del número de variables de estado que tiene el sistema. Pero basta con determinar uno de ellos.
Observando la figura 7, se considera un punto cualquiera xt en el momento t, el cual es perturbado una distancia Et y se obtiene otro punto xt E t. En los sistemas caóticos la perturbación crece exponencialmente ![]() lo que es equivalente a
lo que es equivalente a ![]() y la perturbación en el instante t =0 es siempre muy pequeña. Finalmente, el exponente de Lyapunov está definido por:
y la perturbación en el instante t =0 es siempre muy pequeña. Finalmente, el exponente de Lyapunov está definido por:

Como las trayectorias van separándose con el tiempo, el exponente de Lyapunov debe cumplir con la condición de ser positivo λ > 0. Además, si se grafica:
![]()
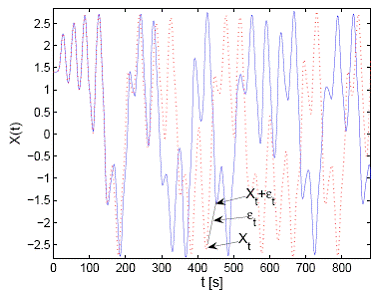
Figura 7. Sensibilidad a las condiciones iniciales en el sistema de Chua con = 100, β = 418. La serie temporal sólida tiene una condición inicial (1.4,0.19,0.01) y la punteada (1.41,0.19,0.01).
considerando el tiempo t y el ![]() se tiene una curva cuya pendiente es positiva.
se tiene una curva cuya pendiente es positiva.
En general, el exponente de Lyapunov puede calcularse numéricamente con la rutina computacional Lyapuk que corresponde al software TISEAN [14 El resultado de esta rutina es un conjunto de datos que vienen a ser los logaritmos naturales, por lo tanto, estos deben ser graficados y ajustados a una recta para obtener la pendiente λ.
Como el sistema tiene tres variables, existen también tres exponentes, pero sólo basta con que un de ellos sea positivo para considerar una región como caótica. Sin embargo, para tener una información más completa sobre las periodicidades, es importante tener en cuenta el resto de los exponentes.
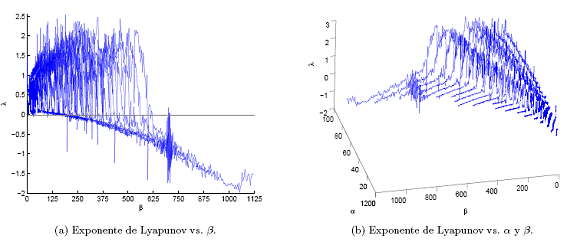
Figura 8. Espectros de Lyapunov para -y mínimo, la región caótica es amplia. Caos se encuentra cuando λ > 0.
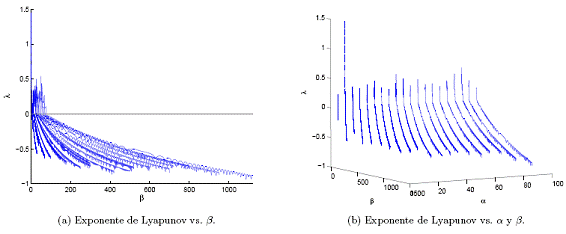
Figura 9. Espectros de Lyapunov para -y máximo, la región caótica es angosta.
4.2. Metodología y Resultados Para Obtener el Exponente y el Espectro de Lyapunov
Para comprobar las regiones caóticas del sistema de Chua considerando dos parámetros, se guardaron los datos proporcionados por la integración numérica para un a y un a (ya sea el mínimo o el máximo) en un archivo *.dat y se consideró solamente el 80 % de estos datos con el fin de descartar los transientes.
A continuación, se introdujo el archivo *.dat en la rutina (Lyap-k) del software TISEAN y se hizo correr según las instrucciones que se indican en la bibliografía [12].
Se graficó el nuevo archivo de datos que proporciona Lyap-k, se obtuvo la pendiente de la curva y se verificó que los exponentes eran positivos.
Considerando el tercer parámetro, se prosiguió de la misma manera que en la anterior caracterización y se comprobó que el exponente era positivo en cada límite.
Además, se obtuvo el espectro de Lyapunov, esta vez se utilizó una rutina que proporcionaba todos los exponentes de Lyapunov para varios valores de β Es decir, para un y un γ (ya sea mínimo o máximo), se hizo correr el valor de β en pasos pequeños, luego se tomó cada serie temporal de la variable X y para cada una de ellas se calculó el exponente de Lyapunov utilizando la ecuación (4).
Este procedimiento se ha realizado para todos los valores de a que varía en pasos de
Estos espectros dan una idea más general de la región caótica y sirven para corroborar los resultados de la caracterización con dos parámetros.
Se encontró el espectro de Lyapunov respecto de y β para el γ mínimo y para el γ máximo. Se observa que para el γ mínimo, el espectro informa que existen regiones caóticas para todo valor de a y una amplia región de β
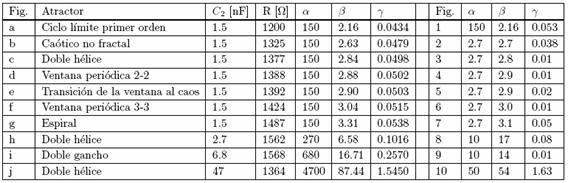
TABLA 3
Para las figuras (a)-(j) se tienen los datos de los componentes con los cuales se obtuvieron los atra.ctores en laboratorio y los correspondientes valores de parámetros para el modelo. Para las figuras (1)-(10) se tienen los valores de los parámetros más adecuados para obtener los mismos atractores con el modelo.
con varias ventanas periódicas. Para este 'y, se tiene el espectro de Lyapunov con respecto a β (ver Fig. 8(a)), en él se observa una región caótica para ![]() , con ventanas periódicas en varios puntos, y el paso a la periodicidad a partir de β = 726. Luego, el espectro de Lyapunov con respecto a los dos parámetros y β se presenta en la figura 8(b), en la cual se tiene una región caótica ya a partir de = 0, y lo mismo para β = 0, posteriormente, cuando = 30, comienzan a aparecer las ventanas periódicas y a partir de β= 200, sucede lo mismo. La región caótica va creciendo a medida que y β aumentan. Este resultado va en aceptable concordancia con las regiones de la figura 6 y de igual modo con la figura 4.
, con ventanas periódicas en varios puntos, y el paso a la periodicidad a partir de β = 726. Luego, el espectro de Lyapunov con respecto a los dos parámetros y β se presenta en la figura 8(b), en la cual se tiene una región caótica ya a partir de = 0, y lo mismo para β = 0, posteriormente, cuando = 30, comienzan a aparecer las ventanas periódicas y a partir de β= 200, sucede lo mismo. La región caótica va creciendo a medida que y β aumentan. Este resultado va en aceptable concordancia con las regiones de la figura 6 y de igual modo con la figura 4.
En cambio, para el γ máximo, el espectro indica que las regiones caóticas se tienen para todo valor de pero con regiones muy angostas de β (ver Fig. 9(a)). Esto implica que cuando γ va llegando a su máximo valor y toma valores grandes, entonces la tendencia del sistema es hacia la periodicidad. Una vista global se observa en
Estos espectros ayudan a completar la información obtenida para el sistema con dos parámetros, además el espectro del exponente de Lyapunov nos da una información global del comportamiento del sistema cuando sus parámetros varían.
Experimentalmente, se observó que cuando = 150 se formaban variedades de atractores con una región caótica amplia y con ventanas periódicas, en cambio para = 4700 se obtuvo menor variedad de atractores y no fue posible observar ventanas periódicas. Al aumentar el valor del potenciómetro, γ y β también aumentan, por lo tanto, sí fue posible observar que el sistema tendía a ciclos límite y puntos fijos cuando la resistencia llegaba a los 2 k9, tal cual describe el espectro de Lyapunov para el γ máximo.
5. ALGUNAS OBSERVACIONES EXPERIMENTALES
Experimentalmente, los siguientes componentes:
C1 = 10 pF y L=1 mH (ro = 24.1 1-2) fueron las piezas clave para encontrar caos. C2 pudo adquirir valores desde los 1.5 nF hasta los 47 nF y R desde O Ç hasta los
γ = 0.01. Mayor concordancia se obtuvo en los valores experimentales y numéricos de γ, un tanto de ,β y mayores problemas se obtuvieron en los valores de . A pesar de no haber obtenido la correspondencia esperada entre resultados experimentales con la tabla de caracterización numérica, se obtuvieron los atractores característicos del sistema, entre los cuales están el atractor de doble hélice, el atractor espiral, el atractor de doble gancho, ventanas periódicas 2-2, 3-3 y ciclos límite de primer y segundo orden (ver Figs. 10-13). Es importante mencionar que en el modelo, se mantuvieron constantes a y b, las cuales dependen de la resistencia. Por lo tanto, según el modelo lo que variaba al cambiar β γ era en realidad la inductancia. Sin embargo, en el experimento, el componente variable fue la resistencia puesto que una inductancia variable es más difícil de conseguir. Al parecer, este detalle influye en la concordancia entre resultados experimentales y numéricos.
6. ESTUDIO DEL CIRCUITO RL-DIODO
En general, se dice que para observar comportamientos caóticos, es necesario que el sistema sea de tercer
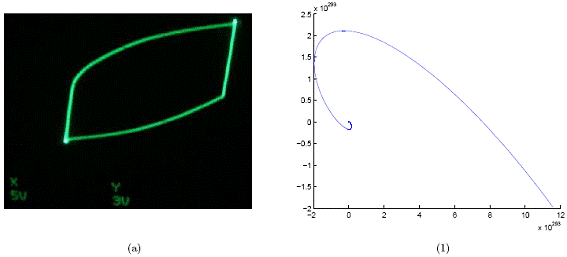
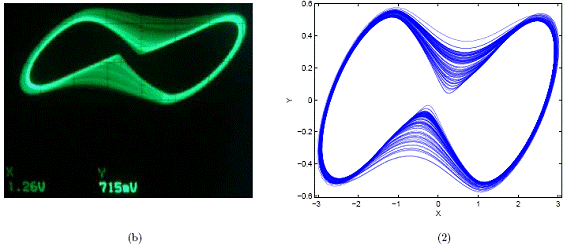

Figura 10. Las imágenes (a)-(c) corresponden a los atractores obtenidos en laboratorio y las imágenes (1)-(3) corresponden a los obtenidos con el modelo. X y Y se miden en voltios en laboratorio.
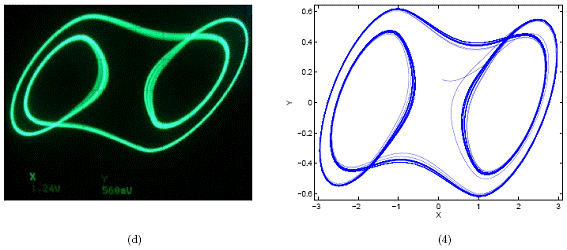
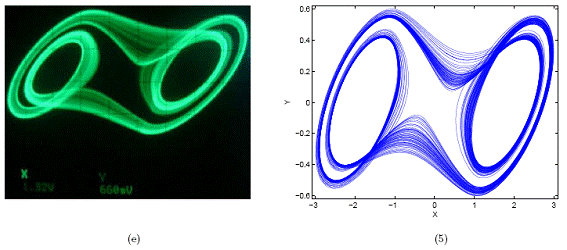
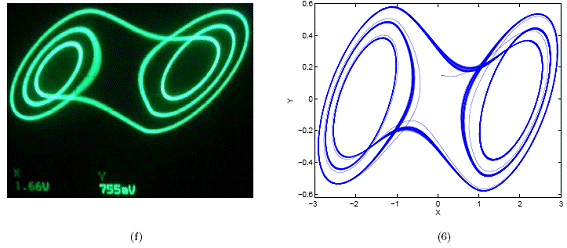
Figura 11. Las imágenes (d)-(f) corresponden a los atractores obtenidos en laboratorio y las imágenes (4)-(6) corresponden a los obtenidos con el modelo. X y Y se miden en voltios en laboratorio.
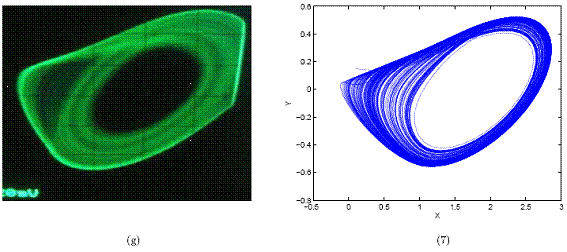

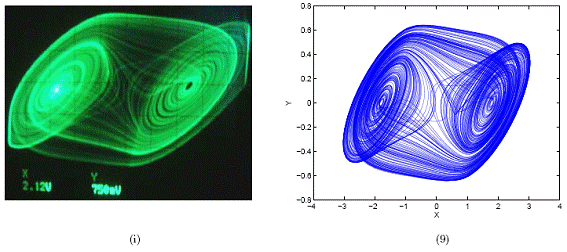
Figura 12. Las imágenes (g)-(i) corresponden a los atractores obtenidos en laboratorio y las imágenes (7)-(9) corresponden a los obtenidos con el modelo. X y Y se miden en voltios en laboratorio.
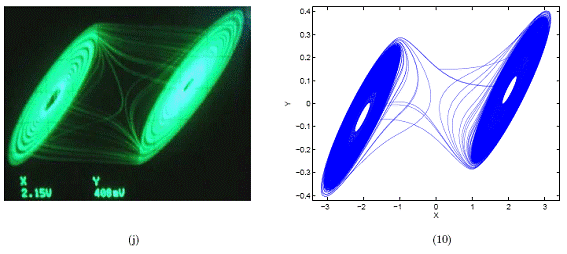
Figura 13. La imagen (j) corresponde al atractor obtenido en laboratorio y la imagen (10) corresponde al obtenido con el modelo. X y Y se miden en voltios en laboratorio.
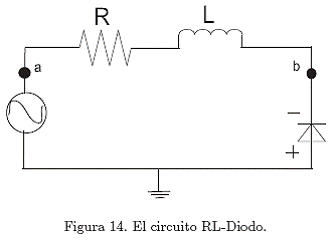
orden o mayor. En el caso de los circuitos autónomos, se necesita que el sistema se componga de un elemento no lineal y por lo menos tres elementos lineales que almacenen energía (inductor, resistencia, capacitor), como se ha visto con el circuito de Chua, es autónomo porque no necesita de fuentes de energía alterna ya que es el mismo circuito el que transforma la señal continua proveniente del diodo en alterna, además el diodo de Chua es la pieza clave para el comportamiento no lineal de todo el circuito. No obstante, ésta regla no es definitiva puesto que puede existir caos en un sistema más sencillo compuesto por una resistencia lineal, un inductor lineal, un diodo normal y una fuente de voltaje. El circuito RL-Diodo, al contrario tiene una fuente de energía alterna, por lo que se lo denomina no autónomo, y tres elementos que bajo ciertos parámetros de frecuencia y amplitud, se generan señales aperiódicas mediante el desdoblamiento de periodo de la tensión en el diodo.
Entonces, a un circuito RLC se reemplaza el condensador por un diodo normal (ver Fig. 14), el cual al ser un elemento no lineal, es el causante de las aperiodicidades. En este circuito se asume que el voltaje de la fuente tiene la forma Va, = Vo cos wt y cuando el voltaje es positivo, el diodo conduce y se produce una caída de voltaje Vb = -Vf. En el estado no conductor, el diodo se comporta como un capacitor, el cual presenta una corriente de carga y el voltaje sigue la frecuencia de la fuente.
La amplitud del voltaje de fuente λ = Vo es el parámetro de control. Esta amplitud no necesariamente es igual para cada ciclo porque cuando la corriente llega a cero, el diodo continúa conduciendo con un tiempo ![]() , donde |Іm| es la corriente máxima durante ese ciclo,
, donde |Іm| es la corriente máxima durante ese ciclo, ![]() el tiempo máximo constante,
el tiempo máximo constante, ![]() el tiempo de recuperación e Ic es constante. Por lo tanto, dependiendo del parámetro Vo, el voltaje en el diodo Vb se repite con un periodo y se va desdoblando hasta llegar
el tiempo de recuperación e Ic es constante. Por lo tanto, dependiendo del parámetro Vo, el voltaje en el diodo Vb se repite con un periodo y se va desdoblando hasta llegar
al caos. Como el voltaje en el diodo depende del voltaje de la fuente y éste depende también de la frecuencia f = w/27r, se espera un comportamiento similar con su variación [13].
Uno de los caminos más comunes para llegar a un comportamiento caótico es el desdoblamiento de periodo en el que las bifurcaciones mediante éste fenómeno ocurren solamente con soluciones periódicas o trayectorias que bajo un punto de bifurcación tienen periodo T y bajo otro punto de bifurcación sufren un cambio ligero presentando un periodo 2T. En el espacio de fases se observaría un ciclo límite (un lazo) que bajo cierto parámetro se convertiría en un ciclo límite de segundo orden (dos lazos) y así sucesivamente los lazos continuarían desdoblándose al igual que las soluciones con un periodo Tk = 2kT0 donde k = 0, n. Si se observa este proceso es muy probable que el sistema llegue a ser caótico [14].
Una característica del desdoblamiento de periodo es que los puntos de bifurcación (parámetros de control) k convergen geométricamente al llegar a la región caótica. Este valor llegó a ser universal por presentarse en varios sistemas caóticos y se denomina la primera constante de Feigenbaum:
![]()
Existe también otro comportamiento universal en las soluciones X(t) de un sistema, o Vb en este caso, definido por:
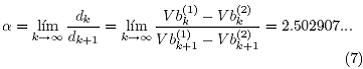
Siendo ![]() dos soluciones de una ramificación en un punto de bifurcación
dos soluciones de una ramificación en un punto de bifurcación
6.1. Metodología y Resultados Para Estudiar el Circuito R-L-Diodo
Primero, se armó el sistema según el diagrama de
Luego, se encontró la frecuencia en la cual al variar la amplitud, el sistema presentaba bifurcaciones y caos. A esta frecuencia, se hizo variar la amplitud del voltaje de fuente y se observó el cambio de periodo en la serial del diodo hasta encontrar el valor de voltaje de fuente en el que ocurren los comportamientos caóticos. Se anotaron los valores Vo y se procedió a calcular la primera constante de Feigenbaum á. Además se hizo el intento de medir los valores de voltaje en el diodo correspondientes a cada punto de bifurcación y calcular la segunda constante a. Posteriormente, estos puntos fueron graficados.
Por otra parte, se observó el comportamiento del sistema cuando el voltaje queda fijo y la frecuencia varía.
El comportamiento del diodo se ve afectado sobretodo a frecuencias altas (1 MHz-3 MHz) y/o a amplitudes altas. Se encontró que a partir de f=195.3 kHz se observan bifurcaciones que llegan a regiones caóticas cuando el valor del voltaje de fuente Vo cambia. Esta frecuencia no es la misma para todos los diodos, a pesar de que todos sean de la misma serie 1N4007.
Este sistema permite apreciar con claridad el proceso de bifurcación, en el que la ruta hacia el caos es el desdoblamiento de periodo de la tensión en el diodo. Al principio, se presentan ciclos límite de primer orden, luego el orden aumenta y se ingresa a una región caótica bastante angosta, a continuación el sistema pasa a una ventana periódica. Posteriormente, ingresa otra vez a otra región caótica, luego se presenta otra ventana periódica más angosta que la primera y finalmente el sistema permanece en una región caótica. Fotografías de los estados de este proceso se observan en Fig. 15.
A continuación, se calcula la constante de Feigenbaum para la primera región caótica. Los valores que dan el mejor valor de la constante son: 1315 mV, 1415 mV, 1540 mV, 1610 mV y 1630 mV.
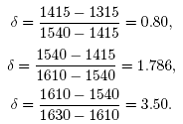
Para la segunda región caótica, se consideran los siguientes valores: 10850 mV, 11750 mV, 12550 mV, 13300 mV, 14400 mV, 14750 mV, 14830 mV. La constante da:
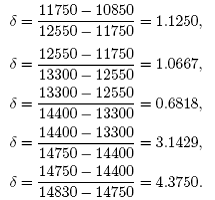
Para la segunda constante de Feigenbaum, se obtiene una aproximación con los valores:
![]()
Las constantes obtenidas cerca de las regiones caóticas no concuerdan con los valores teóricos porque Vb debe ser medido con mayor precisión y además debe ser elegido adecuadamente.
Por otro lado, se estudió el comportamiento del sistema manteniendo fijo el valor de la amplitud y variando la frecuencia. Se encontró que el comportamiento caótico ocurre a partir de Vo = 3.700 V. Se observan similares bifurcaciones en las siguientes frecuencias: 477.8 kHz, 482.2 kHz, 573.4 kHz, 585.9 kHz, 609.6 kHz, 619.8 kHz, 622.3 kHz)y en 677.7 kHz el sistema ingresa a la región caótica (ver Fig. 16), manteniéndose en ese estado hasta que en la frecuencia máxima de 1003.8 kHz el sistema pasa a una ventana periódica y permanece en esa situación. El atractor en esta región es un ciclo límite, el cual luego sufre un desdoblamiento. La frecuencia máxima a la cual se pudo llegar fue 2044.5 kHz, por lo que se ha visto, a frecuencias altas el diodo se comporta de forma totalmente distinta a la conocida.
Con estos resultados se obtuvo la constante de Feigenbaum:
![]()
Estos resultados llevan a pensar que el sistema se encuentra en una región caótica, de todos modos, es necesario mayor precisión en las medidas. Debe tenerse en cuenta que tanto la frecuencia como el voltaje eran variables durante el experimento, lo que también puede introducir error en los datos. Utilizando una interfase experimentocomputadora y analizando el espectro de potencias de las seriales se obtendrían resultados con menor error.
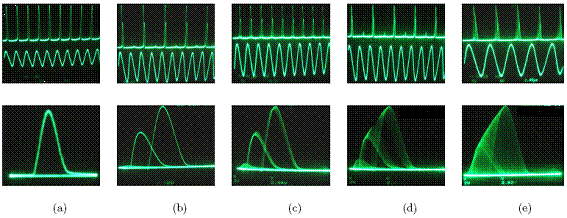
Figura 15. La ruta hacia el caos en el sistema es el desdoblamiento de periodo. (a) Primera bifurcación en Vo = 10850 mV, (b) Segunda bifurcación en 1/0 = 11750 mV, (c) Tercera bifurcación en Vo = 13300 mV, (d) Una cuarta bifurcación de orden difícil de distinguir en Vo = 14400 mV, (e) Finalmente el sistema permanece en la región caótica a partir de Vo = 15200 niV.
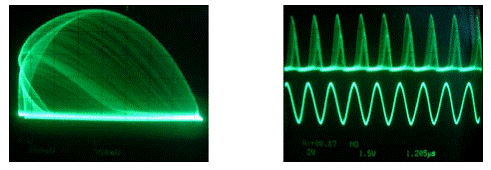
Figura 16. El sistema funcionó a la amplitud Vo = 3.700 V. Izquierda: El atractor caótico en f=677.7 kHz en modo XY. Derecha: La correspondiente serie temporal.
7. CONCLUSIONES Y PERSPECTIVAS
La caracterización numérica del circuito tipo Chua dió corno resultado una región caótica bastante amplia que crece proporcionalmente con los parámetros a y f3, además queda mejor definida si se toma en cuenta el tercer parámetro -y. Todos los límites caóticos fueron comprobados mediante el exponente de Lyapunov. Con el tercer parámetro, fue posible construir el espectro de Lyapunov, el cual mostró que la región caótica contiene varias ventanas periódicas. Se observó que para los valores mínimos de -y en especial, las regiones caóticas son más amplias y con varias ventanas periódicas. Los estados característicos del sistema al aumentar ,3 y -y para un a fijo en el modelo, se presentan en el orden siguiente: divergencia, que indica un estado inestable, una amplia región de caos y finalmente, periodicidad con tendencia a un punto fijo. Los parámetros adimensionales del modelo están relacionados con los valores de los componentes del circuito, entonces, escogiendo adecuadamente estos valores, se dejó un solo componente como el parámetro de control. En este caso, el parámetro experimental fue el potenciómetro que al alimentar de valor, el circuito presenta, a grandes rasgos, los siguientes estados: perio dicidad (ciclo límite de primer orden), caos (con algunas ventanas periódicas) y nuevamente periodicidad (ciclos límite y punto fijo), muy similar a lo que se obtuvo con el modelo. A pesar de que los valores experimentales de los parámetros a, 0, -y no concuerdan exactamente con los resultados numéricos, se satisfacen las expectativas pues los comportamientos y los atractores característicos del sistema obtenidos en laboratorio y con el modelo, son bastante similares. Posibles causas de esta discordancia podrían ser el hecho de que en el modelo, el componente que realmente variaba era la inductancia, en cambio en el experimento lo que variaba era la resistencia; además de la precisión en la medición y errores de redondeo en el modelo.
El estudio cualitativo del circuito RL-Diodo ha permitido observar satisfactoriamente y con detalle uno de los caminos más comunes hacia el caos: el desdoblamiento de periodo. El parámetro de control fue la amplitud del voltaje de fuente a una frecuencia crítica, pero también se observó lo que ocurría cuando el parámetro de control era la frecuencia a una amplitud crítica. Al aumentar el valor de parámetro, en ambos casos, el comportamiento del sistema es el siguiente: un estado periódico
seguido de un amplio estado caótico con varias ventanas periódicas. Midiendo los puntos de bifurcación en la amplitud y la frecuencia, se calcularon las respectivas constantes de Feigenbaum. Los valores de a presentaron mayor discordancia por la falta de precisión y la dificultad de elegir los valores más adecuados para calcularla.
Se observó que la forma de los atractores dependen de la forma de la curva característica. Por ejemplo, la función del diodo de Chua está compuesta por tres regiones y los atractores se forman sobre ellas para la mayoría de los valores de parámetros, excepto en ciertos casos en los que los atractores se forman sobre una de las regiones (e.g. el atractor "espiral"). En un diodo normal, se tiene una parte de conducción y una parte de no conducción, que conforman dos regiones asimétricas, de modo que el atractor queda delimitado por esta forma. Otro aspecto interesante fue que en el circuito tipo Chua, el cambio de la resistencia causa cambios en la amplitud de las oscilaciones llegando a ser irregulares y terminando en un punto fijo a valores altos de resistencia. De modo similar, en el circuito RL-Diodo los cambios en la amplitud del voltaje de fuente causan cambios en el comportamiento del sistema conduciéndolo a un estado caótico, pero el hecho de terminar en un estado caótico o un estado periódico a amplitudes altas, dependía de la frecuencia del voltaje de entrada. De modo que existe un valor crítico para la frecuencia a partir del cual el sistema termina siempre en una región caótica. Es muy posible que esto haya ocurrido en el circuito tipo Chua, al cambiar los componentes de 10 pF y 1 mH, seguramente se llegó a la frecuencia crítica en la cual el sistema comenzaba a tener comportamientos irregulares. Sin embargo, en este circuito, no ha sido posible observar en detalle el camino hacia el caos, los cambios eran bruscos debido a la resistencia variable. Queda pendiente mejorar la forma de adquisición de datos, por ejemplo, sería recomendable analizar el espectro de potencias de ambos circuitos, además de implementar un modelo teórico para el circuito RL-Diodo. Finalmente, se podría dar inicio a trabajos de investigación sobre otros circuitos no lineales y buscar aplicaciones.
REFERENCIAS
1.T. Matsumoto. A Chaotic Attractor from Chua's Circuit, IEEE Trans. Circuits Syst, vol. CAS-31. No. 12, (1984), 1055-1058. [ Links ]
2.L. O. Chua, Chai Wah Wii, A. Huang, and Gtio-Qun Zliong. A Universal Circuit for Studying and Generating Chaos-Part I: Routes to Citaos, IEEE Trans. Circuits Syst, vol. 40. No. 10, (1993), 732-744. [ Links ]
3.L. O. Chua, M. Komuro and T. Matsumoto. The Double Scroll Family, Parts I and II, IEEE Trans. Circuits Syst, vol. CAS-33, No. 11, (1986), 1072-1119. [ Links ]
4.E. Günay, M. AlÇi and R. KiliÇ. A Chaos Synchronization Study: Continuous Implusive Synchronization Between SC-CNN-Based and Chua's Circuit, NDES. (2003), 97- 100. [ Links ]
5.P. Kumar. Roy, S. Chakraborty and S. Kumar Dana. Transition From Complete to Phase Synchronization in Coupled Nonidentical Chua's Oscillators, NDES, (2003), 209-210. [ Links ]
6.K. Murali, K. Thamilmaran and M. Lakshmanan. Rich Variety of Bifurcations and Chaos in a Variant of MuraliLakshmanan-Chua Circuit, (2000). [ Links ]
7. Paul S. Linsay. Period Doubling and Chaotic Behavior in a Driven Anharmonic Oscillator, Physical Review Letters. 47. No. 19 (1981), 1349-1352. [ Links ]
8.J. H. Rivera, E. Duque C., L. E. Avendaño. Síntesis de Redes No Lineales: El Oscilador de Chua, Scientia et Tecnica 24 (2004), 103-106. [ Links ]
9.Michael Peter Kennedy. Experimental Chaos from Autonomous Electronic Circuits., Phil. Trans. R. Soc. Lond. A. 353. No. 1701 (1995), 13-32. [ Links ]
10. Michael Peter Kennedy. Three Steps to Chaos - Part A Chua's Circuit Primer., IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications. 40. No. 10 (1993), 657-673. [ Links ]
11. S. H. Strogatz. Nonlinear Dynamics wid Chaos. AddisonWesley, 1994. [ Links ]
12. R. Hegger, H. Kantz, and T. Schreiber. Practical Implementation of Nonlinear Time Series Methods: The TISEAN Package, Chaos, 9, (1999), 413. [ Links ]














