Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Acta Nova
versión On-line ISSN 1683-0789
RevActaNova. vol.9 no.2 Cochabamba jul. 2019
Artículo Científico
Tiempos necesarios para el establecimiento de equilibrio térmico en el procesamiento de castaña
Una Aplicación de Análisis de Fourier y Problemas de Contorno
Ronanth Zavaleta Mercado, PhD, PE
Profesor Emérito Universidad Católica Boliviana "San Pablo"
ronanth.zavaleta@gmail.com
Recibido: 15 de junio 2019
Aceptado: 10 de julio 2019
Resumen: El tratamiento industrial de castaña requiere de una forma práctica y rápida de poder determinar el tiempo requerido para que el centro de la castaña alcance la temperatura de la superficie, es decir el tiempo requerido para el establecimiento del equilibrio térmico en el procesamiento. A este efecto se realiza la simulación del proceso de calentamiento adoptando una simetría esférica y radios equivalentes. Las soluciones de las ecuaciones diferenciales en derivadas parciales (EDP) que describen el proceso son evaluadas en el centro de la castaña e impuesta la condición correspondiente al equilibrio térmico. Las ecuaciones trascendentes resultantes son evaluadas mediante técnicas numéricas obteniéndose valores del grupo adimensional (Foeq) que cumplen las condiciones impuestas y permiten determinar el tiempo requerido para el establecimiento del equilibrio para diferentes tamaños de castaña.
Dos escenarios fueron estudiados, el primero, despreciando la resistencia externa a la transferencia de calor, mientras que el segundo la incluye. En el primer caso se hace necesario conocer la conductividad térmica efectiva de la castaña y la conductividad térmica efectiva y el coeficiente pelicular en fase gaseosa para el segundo. A pesar de conocerse la solución analítica del problema se requiere de aplicaciones de técnicas de análisis numérico reiteradas habida cuenta de la naturaleza de las soluciones y los requisitos impuestos.
El modelo derivado y resuelto analíticamente puede ser validado experimentalmente por experimentación sencilla en laboratorio.
Palabras clave: castaña, equilibrio térmico
1 Introducción
Se establece un modelo simple no segregado exento de transferencia de masa, de transporte conductivo/convectivo de calor que describe el calentamiento de la castaña sujeta a un ambiente de calefacción en fase gaseosa. Se acepta que una simetría esférica puede en principio adaptarse al tratamiento matemático de la castaña, considerando el radio equivalente como longitud característica. Los problemas de contorno descritos por ecuaciones diferenciales parciales (EDP) lineales y condiciones inicial y límite homogéneas son resueltas en base a aplicaciones de análisis de Fourier, separación de variables o transformadas de Laplace. Las ecuaciones parciales, expresadas en términos de variables adimensionales, son resueltas y evaluadas en el centro de la esfera donde además se impone la condición de equilibrio térmico, es decir la uniformidad de distribución de temperaturas dentro el dominio del problema. Las ecuaciones implícitas y consistentes de series infinitas son resueltas mediante algoritmos numéricos para determinar el grupo adimensional de equilibrio de Fourier (Foeq), que es aquel para el cual se establece el equilibrio térmico (Principio Cero de la Termodinámica). A partir del de este valor se puede determinar los tiempos requeridos para alcanzar el equilibrio para diferentes tamaños de castañas, a condición de que se conozcan algunas propiedades físico-químicas del material, entre ellas la conductividad térmica efectiva, el calor específico y la densidad, y en algunos casos, además de las anteriores, el coeficiente de transmisión de calor por convección.
2 El Modelo
Para la conducción de calor en sólidos la ecuación de conservación de energía en régimen transitorio, al ser combinada con la Ley de Fourier, resulta en1
![]()
donde T es la temperatura, t el tiempo, k la conductividad térmica, ρ la densidad y c la capacidad calorífica especifica. Si se supone que la conductividad térmica k corresponde a un valor medio de temperatura y por lo tanto es independiente de la misma, la Ecuación [1] deviene en
![]()
en la cual ![]() es el coeficiente de difusión térmico. La forma expandida de la Ecuación [2] es
es el coeficiente de difusión térmico. La forma expandida de la Ecuación [2] es
![]()
Si se admite que los gradientes en θ y Φ son nulos y se acepta por lo tanto un modelo conductivo enteramente radial, se obtiene la siguiente EDP lineal, donde T=T(t, r), siendo r la coordenada espacial radial
![]()
La consideración de diferentes interacciones con el entorno da lugar a condiciones límite e inicial que definen diversos problemas de contorno, de los cuales dos son estudiados en el presente trabajo.
3 Resistencia Externa Nula a la Transferencia de Calor
Si se considera despreciable la resistencia a la transferencia de calor en la fase gaseosa, es decir aquella correspondiente a la fase gaseosa de calefacción en sí, entonces la temperatura de la capa exterior de la castaña tiende a la temperatura del medio calefactor, y puede entonces considerarse constante. Si se acepta además que la temperatura externa de la castaña se mantiene constante en un valor To, el problema de contorno queda definido por la Ecuación [4] y las siguientes condiciones límite e inicial
![]()
donde a es el radio equivalente externo, T0 la temperatura externa impuesta, T1 la distribución inicial de temperaturas en la castaña, supuesta constante. Debe cumplirse por supuesto la condición T0 > T1.
La solución analítica del problema transitorio de contorno definido por las ecuaciones [4] y [5] se obtiene de una manera sencilla mediante separación de variables2,3,5,4:
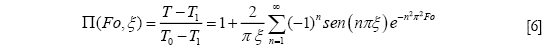
donde ![]() y
y ![]() son respectivamente, la coordenada espacial adimensional normalizada (0 ≤ ξ ≤ 1) y el grupo adimensional de Fourier, mientras que es la temperatura adimensional normalizada, y que comprende, por lo tanto, un dominio 0 ≤ Π ≤ 1. La solución formal de problema (Ecuación [6]) es convergente y uniformemente convergente con respecto a Fo y ξ de acuerdo al criterio de Weierstrass, y satisface la EDP de partida y sus condiciones inicial y límite. Se puede demostrar, además, la convergencia uniforme de la solución mediante el Criterio de Cauchy y la unicidad de esta solución por aplicación del criterio de Abel.5,7
son respectivamente, la coordenada espacial adimensional normalizada (0 ≤ ξ ≤ 1) y el grupo adimensional de Fourier, mientras que es la temperatura adimensional normalizada, y que comprende, por lo tanto, un dominio 0 ≤ Π ≤ 1. La solución formal de problema (Ecuación [6]) es convergente y uniformemente convergente con respecto a Fo y ξ de acuerdo al criterio de Weierstrass, y satisface la EDP de partida y sus condiciones inicial y límite. Se puede demostrar, además, la convergencia uniforme de la solución mediante el Criterio de Cauchy y la unicidad de esta solución por aplicación del criterio de Abel.5,7
La temperatura en el centro de la castaña se determina tomando el límite cuándo r ![]() 0 y por consiguiente ξ
0 y por consiguiente ξ ![]() 0 en la Ecuación [6], levantándose la indeterminación resultante por aplicación de la Regla de L'Hôpital
0 en la Ecuación [6], levantándose la indeterminación resultante por aplicación de la Regla de L'Hôpital
![]()
Cuando se alcanza el equilibrio térmico, definido por la Ley Cero de la termodinámica, debe cumplirse que T ![]() T0 correspondiente a Π
T0 correspondiente a Π ![]() 1 y por lo tanto debe satisfacerse la siguiente ecuación
1 y por lo tanto debe satisfacerse la siguiente ecuación
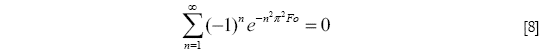
Esta ecuación implícita trascendente puede resolverse para obtener un Foeq asociado con el tiempo para el establecimiento del equilibrio térmico en la castaña, y por lo tanto proporciona el tiempo requerido para que el centro alcance la misma temperatura que la superficie:
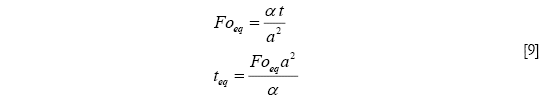
Al sustituir ![]() , donde ke es la conductividad térmica efectiva, ρ la densidad y c la capacidad calorífica específica en la Ecuación [9], se tiene en definitiva que
, donde ke es la conductividad térmica efectiva, ρ la densidad y c la capacidad calorífica específica en la Ecuación [9], se tiene en definitiva que
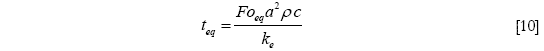
Alternativamente, si se determina experimentalmente el tiempo requerido para alcanzar el equilibrio, la conductividad efectiva puede determinarse a partir de la Ecuación [10].
4 Resistencia Externa Finita a la Transferencia de Calor
En este caso la resistencia a la transferencia de calor correspondiente al medio calefactor no puede ser despreciada y debe ser incorporada en el análisis. Como la interfase sólido-gas puede considerarse de capacidad calorífica nula y no puede en consecuencia almacenar energía, el principio de conservación de energía conduce a que la interacción de calor predominante en el medio gaseoso anexo a la interfase, que corresponde a un mecanismo combinado convectivo-difusivo, debe ser igual en magnitud a aquella interacción del medio sólido, donde predomina un mecanismo conductivo descrito por la Ley de Fourier. Esta aproximación da lugar al siguiente conjunto de condiciones límite e inicial
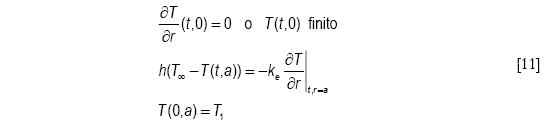
donde h es el coeficiente pelicular de transferencia de calor. Al intentar la solución por separación de variables, estas condiciones conjuntamente a la Ecuación [4] conforman el nuevo problema transitorio de contorno, estrictamente uno de Sturm - Liouville de condiciones homogéneas de contorno tipo Neumann. La solución analítica es2,3,4
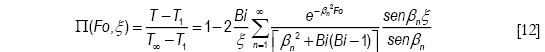
en la que ![]() es el grupo adimensional de Biot, que es el cociente de los dos mecanismos combinados de transporte de calor, convectivo y conductivo, y cuya magnitud indica la predominancia relativa de uno de estos mecanismos, T∞ es la temperatura del medio calefactor, T1 la temperatura inicial supuesta constante, y βn es el vector infinito de autovalores resultante de la solución de la ecuación cuyo parámetro es Bi
es el grupo adimensional de Biot, que es el cociente de los dos mecanismos combinados de transporte de calor, convectivo y conductivo, y cuya magnitud indica la predominancia relativa de uno de estos mecanismos, T∞ es la temperatura del medio calefactor, T1 la temperatura inicial supuesta constante, y βn es el vector infinito de autovalores resultante de la solución de la ecuación cuyo parámetro es Bi
![]()
La solución formal de problema (ecuaciones [12] y [13]), al igual que en el caso anterior, es convergente y uniformemente convergente con respecto a Fo y ξ de acuerdo al criterio de Weierstrass, y satisface la EDP de partida, así como su condición inicial y límite. Se puede demostrar, además, la unicidad de esta solución.6,7
La solución obtenida puede ser evaluada en el centro de la esfera, es decir cuándo ξ ![]() 0. La indeterminación se levanta mediante la Regla de L'Hôpital obteniéndose
0. La indeterminación se levanta mediante la Regla de L'Hôpital obteniéndose
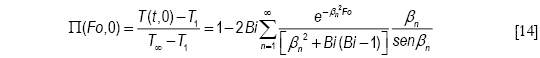
que es la distribución de temperaturas en el centro de la esfera. Cuando se alcanza el equilibrio térmico T(Fo,0) ![]() T∞ y por consiguiente Π(Fo,0)
T∞ y por consiguiente Π(Fo,0) ![]() 1, quedando la Ecuación [14] en
1, quedando la Ecuación [14] en
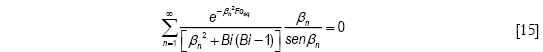
El sistema de ecuaciones [13] y [15] proporcionan un Foeq para cada valor de Bi (ya que Foeq = f (Bi). Por lo tanto, como en el caso anterior, se puede determinar el tiempo para alcanzar el equilibrio, o alternativamente la conductividad efectiva a partir de

a condición de que se determine Foeq = f(Bi).
5 Resultados y Discusión
5.1 Resistencia Externa Nula a la Transferencia de Calor
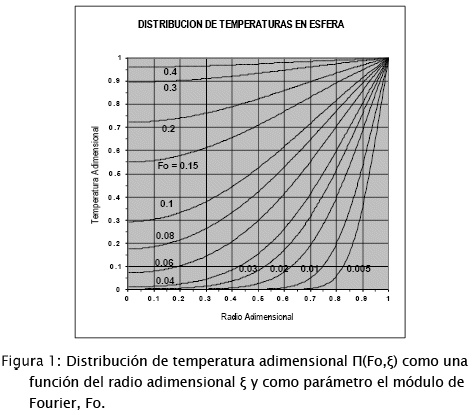
La Ecuación [6] establece la variación de los perfiles de temperatura con el tiempo al interior de la castaña, tal como se ve en la Figura 1:. La temperatura tiende al equilibrio al aumentar el tiempo (incrementándose Fo paralelamente).
El tiempo requerido para alcanzar el equilibrio es tanto mayor cuanto más interno es el punto a considerarse. En procesos de calentamiento el centro de la esfera será el último en alcanzar el equilibrio.
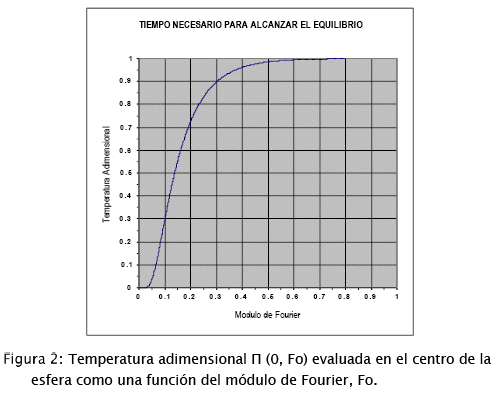
Tal como se puede apreciar en la Figura 2:, existe un tiempo finito (Fo finito) para el cual se alcanza el equilibrio Esta figura es una representación de la Ecuación [7] descriptiva de la dinámica de la temperatura en el centro de la esfera.
Se podría anticipar que debería existir un valor de Fo < ∞ para el cual se cumpla la condición de equilibrio, es decir un Foeq tal que Π![]() 1 cuando Fo
1 cuando Fo![]() Foeq. Este criterio impuesto en la Ecuación [7] permite deducir la Ec. [8], que puede ser resuelta numéricamente para obtener Foeq. Este valor resulta ser igual a 0.802 (valor obtenido utilizando subprogramas de Mathcad 15® de la firma Mathsoft Engineering & Education, Inc).
Foeq. Este criterio impuesto en la Ecuación [7] permite deducir la Ec. [8], que puede ser resuelta numéricamente para obtener Foeq. Este valor resulta ser igual a 0.802 (valor obtenido utilizando subprogramas de Mathcad 15® de la firma Mathsoft Engineering & Education, Inc).
Consecuentemente, la Ecuación [10] se reduce a
![]()
Si se define como V el volumen de la castaña, entonces el radio equivalente a, que es aquel que corresponde a la esfera de igual volumen, está dado por,
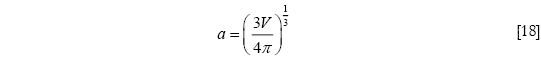
Por lo tanto, de conocerse V, ρ, c y ke es posible determinar el tiempo requerido para que el centro de la castaña alcance la temperatura de la superficie, o alternativamente si se determina experimentalmente teq, puede obtenerse ke.
5.2 Resistencia Externa Finita a la Transferencia de Calor
La solución analítica que comprende las ecuaciones [12] a [16] tiene como parámetro a Bi, y por lo tanto puede anticiparse una solución para cada valor del mismo. Si se decide un valor de Bi puede obtenerse el vector que contenga los autovalores de la solución y por lo tanto evaluarse ésta. Comentarios similares se aplican a las soluciones para el centro de la castaña y para el tiempo requerido para el establecimiento del equilibrio.
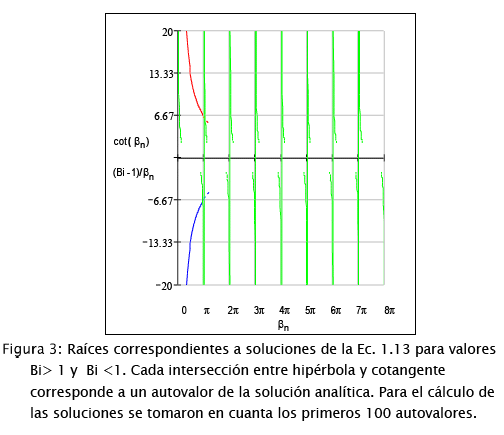
El cálculo de la solución analítica puede volverse engorroso y requiere de aplicaciones reiteradas de algoritmos numéricos y la utilización de computadores digitales. La determinación de un número suficiente de autovalores como para permitir la convergencia de la solución resulta en la determinación de un conjunto importante de raíces (las 100 primeras para el presente trabajo), resultantes de intersecciones de funciones hiperbólicas y cotangentes, como puede apreciarse en la Figura 3:. Cada valor de Bi da lugar a un vector diferente de autovalores, y por lo tanto a soluciones diferentes, para cualquier punto del dominio del problema, así como a un valor nuevo de Foeq.
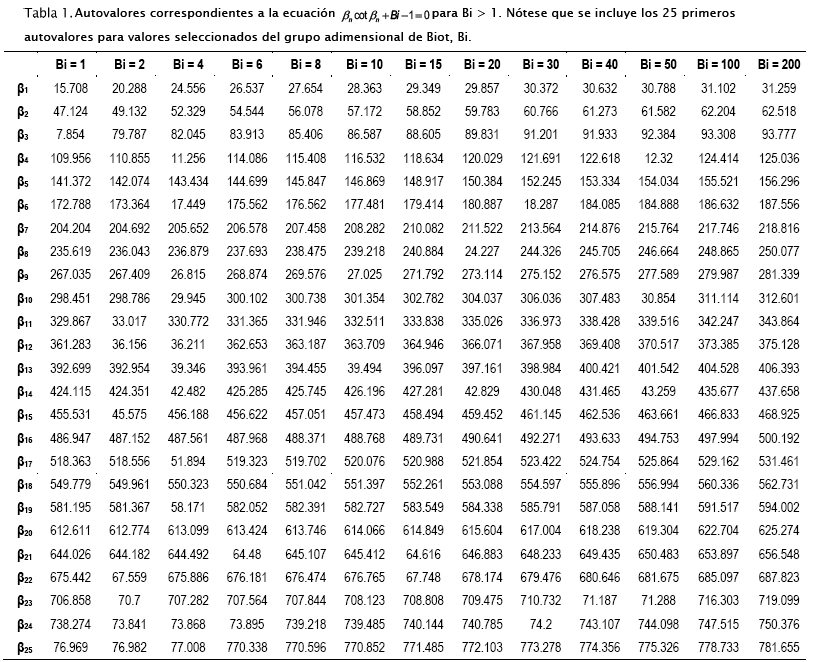
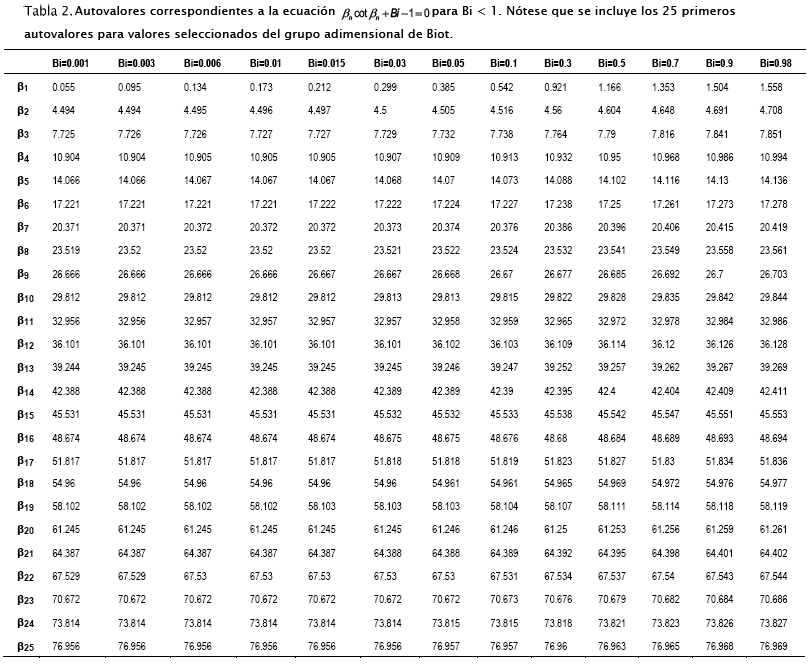
En las tablas 1 y 2 se incluyen los primeros 25 autovalores de la Ecuación [13] calculados para varios valores de Bi, tanto mayores como menores a 1, mediante los subprogramas 1 a 4 escritos en MathCad 15 y que utilizan recurrentemente algoritmos numéricos correspondientes a los métodos de Ridder y alternativamente, el de Brent contenidos en la función root®.
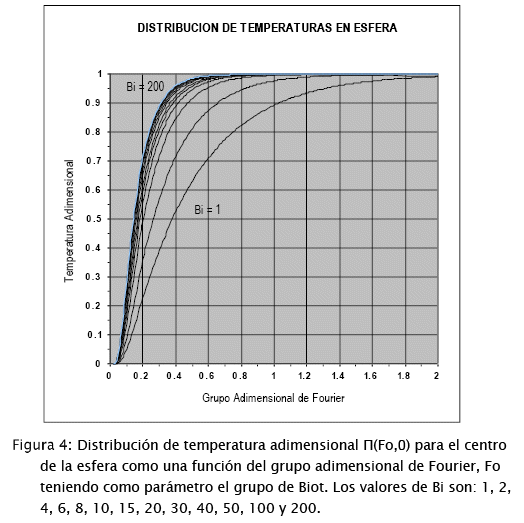
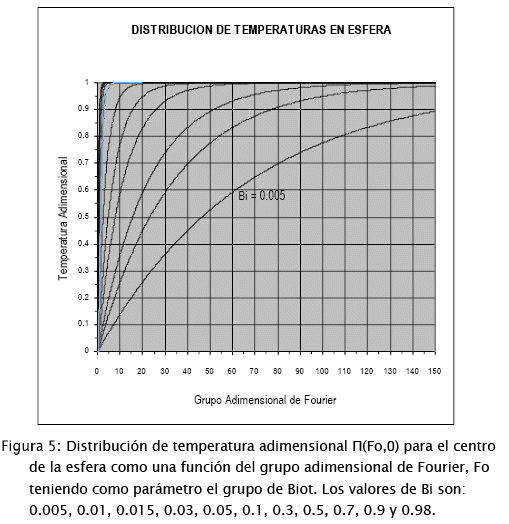
En las figuras 4 y 5 se ha graneado las funciones de la temperatura en el centro de la castaña como una función de Fo teniendo como parámetro a Bi. La Figura 4: corresponde a valores de Bi > 1 y la Figura 5: a valores de Bi < 1. De un modo similar pueden calcularse perfiles para cualquier valor del radio adimensional por aplicación de la solución formal (ecuaciones [12] y [13]).
Los subprogramas 5 a 7 permiten el cálculo de la solución formal, para el centro de la esfera, para varios valores del parámetro Bi, tanto menores a 1 como mayores o iguales a uno, en función de Fo, los mismos que fueron utilizados para la elaboración de las figuras 4 y 5.
Por otra parte, las soluciones de las ecuaciones [13] y [15] obtenidas por aplicaciones reiteradas del subprograma root® de Mathcad 11, utilizando el algoritmo de Müller, y con base a los subprogramas 8, 9 10 y 11, permiten obtener valores de Foeq para arreglos de grupos adimensionales de Bi, tal como se muestra en la Tabla 3, para los casos de Bi < 1 y Bi ≥ 1. Estos valores han sido correlacionados mediante análisis de regresión empleando algoritmos de optimización no lineales.
Las ecuaciones de ajuste para Foeq = Foeq(Bi) son respectivamente para Bi < 1 y para Bi ≥ 1
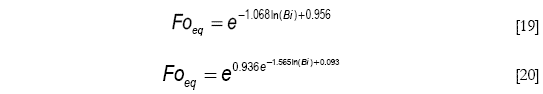
que corresponden respectivamente a las ecuaciones de ajuste siguientes
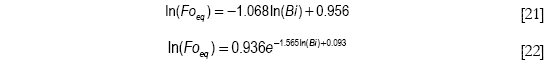
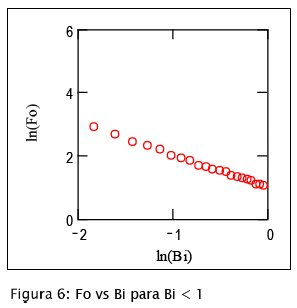
La calidad del ajuste puede apreciarse en las figuras 6 y 7, con coeficientes de correlación de Pearson superiores a 0.98. Por lo tanto, la Ecuación [16] queda ahora totalmente definida y se tienen las siguientes expresiones para los tiempos requeridos para alcanzar el equilibrio en el caso de resistencia externa finita a la transferencia de calor.
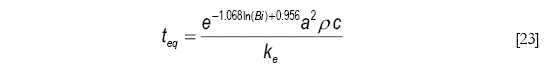
para Bi < 1 y
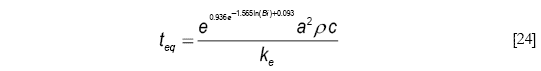
para Bi ≥ 1.
Estas ecuaciones pueden ser utilizadas a condición de que se pueda determinar el coeficiente de transferencia de calor por convección y la conductividad térmica efectiva y de esta manera obtener el Bi correspondiente. Para el primero la literatura es amplia y el segundo puede determinarse experimentalmente.
Se puede diseñar experimentos sencillos conducentes a la determinación de la variación de la temperatura con el tiempo en el centro de las castañas, registrando los tiempos en los que se alcanza la temperatura de equilibrio, y con esta información y la relativa a la geometría de los frutos validar el modelo obteniendo el grupo adimensional de Bi que ajuste los datos. Para hacerlo, los requerimientos computacionales son modestos y requieren cuando más de algoritmos numéricos heurísticos de optimización. El modelo validado entonces podría en principio aplicarse de una manera rutinaria, ajustándolo periódicamente para tomar en cuenta las variaciones naturales en la castaña recolectada, y de esta manera determinar esquemas adecuados de tratamiento, especialmente en lo relativo al secado.

Subprograma 1: Evalúa los primeros n autovalores asociados con la Ecuación [13] para un valor de Bi = α > 1.
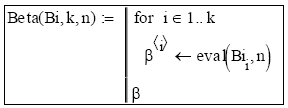
Subprograma 2: Evalúa los primeros n autovalores asociados con la Ecuación [13] para un vector que contiene k valores de Bi > 1 contenidos en el vector columna Bi, que debe definirse previamente.
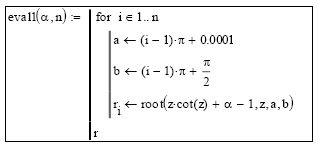
Subprograma 3: Evalúa los primeros n autovalores asociados con la Ecuación [13] para un valor de Bi = α < 1
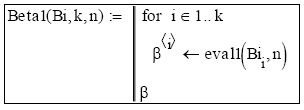
Subprograma 4: Evalúa los primeros n autovalores asociados con la Ecuación [13] para un vector que contiene k valores de Bi > 1 contenidos en el vector columna Bi, que debe definirse previamente.
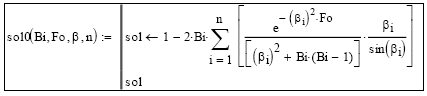
Subprograma 5: Evalúa la temperatura en el centro de la esfera Π(Fo,0) dados Bi, Fo, el vector de n filas β que contiene los n primeros autovalores correspondientes a la Ecuación [13].
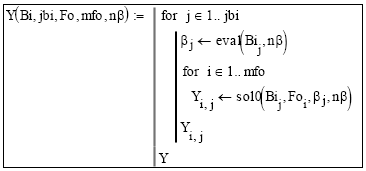
Subprograma 6: Evalúa la temperatura en el centro de la esfera Π(Fo,0) (Ecuación [14]) para todas las combinaciones de valores de Bi. Contenidos en el vector Bi de jbi filas, y los valores de Fo, contenidos en el vector Fo de mfo filas considerando los primeros nβ autovalores correspondientes a la Ecuación [13]. En este caso Bi > 1.
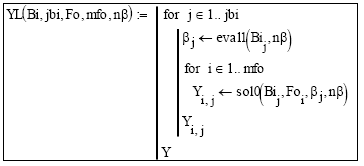
Subprograma 7: Evalúa la temperatura en el centro de la esfera Π(Fo,0) (Ecuación [14]) para todas las combinaciones de valores de Bi contenidos en el vector Bi de jbi filas, y los valores de Fo, contenidos en el vector Fo de mfo filas, considerando los primeros nβ autovalores de la Ecuación [13]. En este caso Bi < 1.
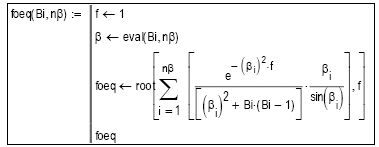
Subprograma 8: Evalúa el valor del módulo de Fourier crítico, Foeq para el cual se establece el equilibrio térmico. Bi es el grupo adimensional de Biot y nβ es el número de autovalores β correspondientes a soluciones de la Ecuación [13] a considerarse en la solución analítica. Soluciones para Bi > 1.
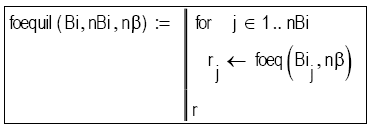
Subprograma 9: Evalúa el valor de los módulos de Fourier crítico, Foeq para todos los valores del vector Bi de valores del grupo de Biot (nBi componentes), tomando en cuenta los primeros nβ autovalores del arreglo β de las soluciones de la Ecuación [13] a considerarse en la solución analítica. Soluciones para Bi > 1.
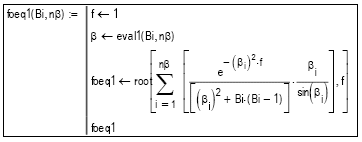
Subprograma 10: Evalúa el valor del módulo de Fourier crítico, Foeq para el cual se establece el equilibrio térmico. Bi es el grupo adimensional de Biot y nβ es el número de autovalores β correspondientes a soluciones de la Ecuación [13] a considerarse en la solución analítica. Soluciones para Bi < 1.
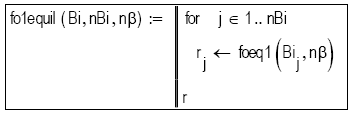
Subprograma 11: Evalúa el valor de los módulos de Fourier crítico, Foeq para todos los valores del vector Bi de valores del grupo de Biot (nBi componentes), tomando en cuenta los primeros nβ autovalores del arreglo β correspondientes a soluciones de la Ecuación [13] a considerarse en la solución analítica. Soluciones para Bi < 1.
Referencias Bibliográficas
[1] Bird R.B., W.E. Stewart y E.N. Lightfoot, “Transport Phenomena”, John Wiley & Sons, Inc 2nd Ed. (2002)
[2] Crank J., “The Mathematics of Diffusion”, Oxford University Press, (1970)
[3] Carlslaw H.S. y J. C. Jaeger, “Conduction of Heat in Solids”, 2nd Ed., Oxford University Press, (1959)
[4] Churchill, R.V., “Operational Mathematics”, 2nd Ed., McGraw-Hill Book Company, (1958)
[5] Churchill, R.V., “Fourier Series and Boundary Value Problems”, 2nd Ed., McGraw-Hill Book Company, (1963)
[6] Lamb, G.L., Jr, “Introductory Applications of Partial Differential Equations”. John Wiley & Sons, Inc. (1995)
[7] Moon, P. y D.E. Spencer, “Partial Differential Equations”, D.C. Heath and Company, (1969)