ARTÍCULOS

 

Interacciones efectivas de largo alcance en una red en la aproximación semiclásica

 

Long-range effective interactions in a lattice in the semiclassical approximation

 

 

Evaristo Mamani†, M. Calcina-Nogales, Diego Sanjinés
Carrera de Física Universidad Mayor de San Andres c. 27 Cota-Cota, Casilla de Correos 8635, La Paz, Bolivia
†Traducción autorizada de "Long-range effective interactions in a lattice in the semiclassical approximation",
E. Mamani, M. Calcina-Nogales and D. Sanjinés, International Journal of Modern Physics B 31 (2017) 1750116.
(Recibido 31 de agosto de 2016; aceptado 13 de enero de 2017)

 

 

---

Resumen

Consideramos el modelo semiclasico de enlace fuerte extendido con un hamiltoniano que comprende interacciones a primeros y a segundo vecinos para una partıcula cargada que se traslada en una red (por el mecanismo de hopping) en presencia de un campo estático arbitrario y un campo uniforme rapidamente oscilante. La aplicación del método de Kapitza permite obtener un hamiltoniano efectivo independiente del tiempo con elementos de salto (hopping) que dependen de los campos externos estatico y oscilante. Nuestros cálculos muestran que la aproximacion semiclásica es bastante buena pues se obtiene, para un campo oscilante homogeneo, los mismos elementos de salto que se derivan del formalismo cuantico. Ademas, controlando el campo oscilante, podemos manipular las interacciones de tal forma de suprimir lo que serían las interacciones dominantes (a primeros vecinos) y dejar así como efectos observables aquellos debidos a lo que de otra manera serían las interacciones remanentes (con vecinos distantes).

Codigo(s) PACS: 42.50.Ct — 03.65.Sq — 72.10.Bg

Descriptores: Hamiltoniano efectivo — aproximacion semiclásica — modelo de enlace fuerte

---

Abstract

We consider the semiclassical model of an extended tight-binding Hamiltonian comprising nearest- and next-to-nearest neighbor interactions for a charged particle hopping in a lattice in the presence of a static arbitrary field and a rapidly oscillating uniform field. The appli-cation of Kapitza's method yields a time independent effective Hamiltonian with long range hopping elements that depend on the external static and oscillating fields. Our calculations show that the semiclassical approximation is quite reliable as it yields, for a homogeneous oscillating field, the same effective hopping elements as those derived within the quantum approach. Furthermore, by controlling the oscillating field, we can engineer the interactions so as to suppress the otherwise dominant interactions (nearest neighbors) and leave as observable effects those due to the otherwise remanent interactions (distant neighbors).

Subject headings: Effective Hamiltonian — semiclassical approximation — tight-binding model

---

 

 

1. INTRODUCCIÓN

El estudio de la dinámica electrónica en redes cristalinas de estado solido adquirió recientemente un renovado interes en vista de la factibilidad de tecnicas experimentales y la posibilidad de imitar (emular) dichos fenomenos dinámicos, por ejemplo, en arreglos de guías de onda opticas (Dreisow et al. 2011, Marte 1997, Lenz 1999, Longhi 2006, Longhi 2007, Longhi 2009, Longhi 2010). De estos efectos, aquellos que resultan de la aplicación de un campo eléctrico externo AC homogeneo son relevantes para dilucidar fenomenos de transporte como, por ejemplo, localización dinámica, control coherente de tunelamiento, transiciones metal-aislante y dinámica de átomos en trampas (Dunlap 1986, Rahav 2003, Bandyopadhyay 2008). Si, además, los campos AC se consideran como perturbaciones de alta frecuencia, es posible entonces aplicar un método de promediación temporal (debido originalmente a P. L. Kapitza para el estudio del pendulo invertido (Kapitza 1965, Landau 1985)) a fin de obtener un hamiltoniano efectivo independiente del tiempo para una red de enlace fuerte. Nuestros resultados permiten manipular las constantes efectivas de tunelamiento en la red, lo que puede ser util para imitar ciertos fenómenos del estado sólido (Itin 2014, Itin 2015). De hecho, fue en estos trabajos donde encontramos el efecto interesante de una interacción a segundos vecinos que surge por la acción conjunta de un campo uniforme rápidamente oscilante y un potencial estático cuadrático. Este resultado, que fue deducido en (Itin 2014) y (Itin 2015) aplicando la técnica de promediación temporal de Kapitza a un hamiltoniano de enlace fuerte, tambien se puede obtener de manera exacta usando el modelo semiclásico1 (lo que hacemos, como un resultado colateral, en este trabajo), llegando así, de una forma mas simple y expedita, a las mismas conclusiones que aquellas que se deducen estrictamente con el formalismo cuantico, específicamente, en el tratamiento de los efectos dinámicos combinados sobre una partícula cargada (electrón) por la acción de campos eléctricos externos arbitrarios dependientes del tiempo y de la posición.

El propósito de nuestro trabajo es aplicar el modelo semiclásico a una red extendida de enlace fuerte y, además de confirmar fenómenos conocidos, deducir nuevos efectos que sugieren la posibilidad de obtener ("diseñar") hamiltonianos efectivos usando campos perturbativos de alta frecuencia. A fin de contrastar y verificar nuestros resultados nos referiremos a Martínez et al. (2014) donde el metodo de Kapitza se usa para calcular un potencial efectivo independiente del tiempo debido a un campo rapidamente oscilante y a un campo estático arbitrario (en Martínez et al. (2014) se puede asimismo encontrar algunas referencias acerca de la aplicacion del modelo semiclásico a redes de enlace fuerte). La idea de usar un hamiltoniano extendido de enlace fuerte que incorpore una interaccion a segundos vecinos (o vecinos mas distantes) se puede rastrear, por ejemplo, hasta el trabajo de Dunlap & Kenkre (1986), donde sus resultados acerca de la localizacion dinámica se extienden a interacciones de largo alcance a traves de una energía cinetica de la forma 2 Pn An cos nap, generalizando así la interaccion usual a primeros vecinos dada por 2Acosap. El concepto de "diseno de la banda" (band engineering) con interacciones de largo alcance fue investigado (de manera teorica y experimental) en redes fotonicas, por ejemplo en Dunlap & Kenkre (1986), donde se suprime aproximadamente la difraccion de banda ancha en un haz de luz. Investigaciones recientes en sistemas laminados de grafeno muestran que los efectos correspondientes a los terminos adicionales de un hamil toniano extendido se pueden considerar como mejoras a los resultados sin tales terminos (Reich et al. 2002; Kundu 2011; Wright et al. 2009; Kadirko et al. 2013), aunque esas mejoras son pequenas debido a la menor magnitud relativa de la interaccion a segundos vecinos comparada con la interaccion a primeros vecinos. Para obtener uno de los nuevos resultados de nuestro trabajo controlamos los parametros del campo externo oscilante del tal forma que la interaccion a primeros vecinos se suprime de manera efectiva dejando como interaccion dominante la de segundos vecinos; el efecto observable es una "oscilacion efectiva de Bloch". De la misma forma, la interaccion a terceros vecinos se vuelve dominante cuando las interacciones a primeros y a segundos vecinos se suprimen. Aunque estos resultados se restringen al caso en una dimension, pensamos que su generalizacion a dos y tres dimensiones es posible, de tal forma de poderse aplicar en sistemas reales como por ejemplo el grafeno. De hecho, en Madison et al. (1998) se reporto la primera observación de supresion dinámica de la banda debida a un campo externo AC en una red optica (en lugar de una red de estado solido) donde el ancho de banda se reduce a cero y los estados de Bloch se localizan cuando la amplitud del campo obedece la misma condicion que reportamos en este trabajo, aunque el colapso completo de la banda reportado en Madison et al. (1998) no fue posible en ese experimento debido a acoplamientos con vecinos distantes y la presencia de otras bandas.

Así, podemos resumir la metodología de nuestro trabajo como la aplicacion de un procedimiento a dos modelos: el metodo de promediación temporal de Kapitza aplicado a un modelo de enlace fuerte extendido bajo la aproximacion semiclásica. Organizamos nuestro trabajo de la siguiente manera: en la seccion 2 deducimos la fórmula para el hamiltoniano efectivo aproximado hasta terminos del orden w ^-2 de la frecuencia del campo externo; en la seccion 3 proponemos un modelo de escenario para la ingeniería de interacciones con base en los resultados de la seccion 2; en la sección 4 aplicamos el metodo pseudoespectral para resolver numericamente la ecuación de Schródinger y luego poder comparar los resultados semiclasicos con los cuanticos en el límite w -> ∞; en la seccion 5 discutimos las principales conclusiones que se obtienen de la expresion para el hamiltoniano efectivo y de su aplicacion a la ingeniería de interacciones; en la seccion 6 mencionamos los aspectos concluyentes mas relevantes y algunas perspectivas interesantes para eventuales trabajos futuros.

 

2. DEDUCCIÓN DEL HAMILTONIANO EFECTIVO

Consideremos el hamiltoniano extendido de enlace fuerte con interacciones a primeros y a segundos vecinos,

donde a es la constante de red; por simplicidad tomemos los valores numericos de las constantes físicas e y h iguales a 1, asimismo supondremos que a = 1 de aquí en adelante; U(x) es el potencial que corresponde a un campo externo estatico arbitrario y f(wt) es un campo rapidamente oscilante con frecuencia w>> 1/T, donde T es el periodo característico de oscilacion de la partícula en ausencia del campo forzador f(wt). A continuacion usamos las ecuaciones de movimiento de Hamilton de las que se obtiene las derivadas temporales de la posicion y del momentum:

Usaremos la notación: U'(x),U''(x),U⁽ⁿ⁾(x), para las derivadas espaciales de U(x). Apliquemos a continuacion la transformación canónica entre los momentos, (x,p) -->(x,y):

donde se definio el "momentum desplazado" y(t) junto con la derivada temporal g(t) = f(wt). Esta transformacion será conveniente para los propósitos que se explican despues de (9). La sustitución de (4) en (2) y en (3) conduce al sistema de ecuaciones:

Debido a la accion combinada de los campos estático y oscilatorio, la partícula realizara un movimiento rapido con pequeñas oscilaciones en torno a una trayectoria que varıa lentamente. Se definen pues las coordenadas "lentas" X(t), Y(t) y las coordenadas "rapidas" éstas últimas se consideran perturbaciones de las primeras:

donde de tal forma que el promedio temporal de se anula en el intervalo temporal con periodo , mientras X(t) y Y(t) permanecen casi constantes en ese mismo intervalo, i.e., = 0, (X) = X(t), (Y) = Y(t).

El conjunto de las transformaciones (x,p) -> (x, y) ->(X, Y) dadas en (4), (7) y (8) es canonico ya que la estructura de las ecuaciones de Hamilton se preserva (Landau & Lifschitz 1985):

esto es así como una consecuencia de la invariancia de los corchetes de Poisson: [p, x] = [y, x] = [Y, X] = 1, lo que conduce a H (x,y;t) = H(x,p;t) + dF (x,y;t)/dt, y la promediacion temporal que se usa como (X) = X(t), (Y) = Y(t), lo que nos lleva de H(x,y;t) a H(X, Y). La forma necesaria de la funcion generatriz es F(x,y;t) = x(y-g) tal que H(x,y;t) = -2Acos(y-g) - 2Bcos2(y - g) + U(x) junto con las condiciones dF/dx = p = y - g y dF/dy = x. El resultado es el desplazamiento de la dependencia temporal del término xf(wt) en H(x,p;t) hacia los argumentos de los operadores de energía cinetica en H(x,y;t), lo que resulta en una transformacion conveniente a fin de obtener promedios temporales de manera eficiente. H(X, Y) tiene ahora la forma de un hamilto-niano explıcitamente independiente del tiempo que representa a una constante de movimiento y cuya construccion conducirá a la Eq. (42), que es el resultado central de este trabajo.

Comenzamos ahora el procedimiento de promediacion temporal reemplazando (7) en (5), y (8) en (6):

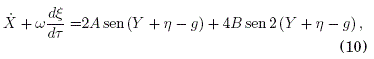
donde d/dt = wd/dt. Luego obtenemos el promedio temporal de (10) y (11):

Las ecuaciones (12) y (13) son las ecuaciones de movimiento efectivas que corresponden a las partes lentas de las coodenadas x(t), y(t), respectivamente. De manera similar, las ecuaciones de movimiento efectivas que corresponden a las partes rapidas de las coordenadas x(t), y(t), se obtienen restando (12) de (10), y restando (13) de (11):

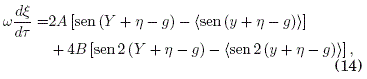
Para resolver el sistema (14)-(15) para las coordenadas rapidas definimos: t como el "tiempo lento", t = wt como el "tiempo rpido" y E= t/r = 1/w como el parametro de pequenez tal que E -> 0 cuando w->∞. Ahora realizamos la expansion de en potencias de E:

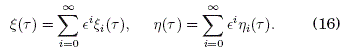
Sustituyendo (16) en (14) y en (15) hasta E², obtenemos:

 

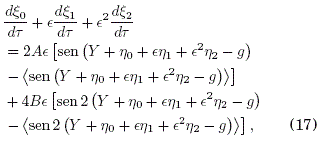
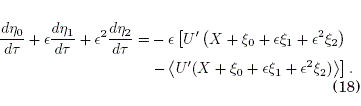
Expandimos tambien hasta E² las funciones sen(•) y U'(•) en el lado derecho de (17) y (18):

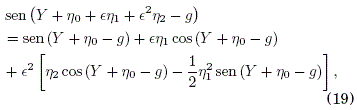
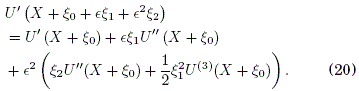
La sustitucion de (19) en (17) y de (20) en (18), y la comparacion de los términos en los mismos órdenes de potencias de E, conducen a la siguientes relaciones: para E⁰,

con la solución E₀ = N₀ = 0 elegida de tal forma que los promedios temporales de se eliminen. Para E¹ tenemos:

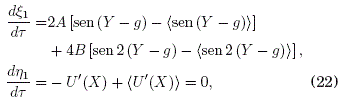
con la solucion N₁ = 0 para la ultima ecuación. Para E² tenemos:

 

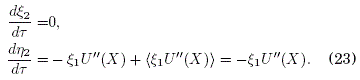
con la solución E₂ = 0 para la primera ecuacion. Notese que para dadas en (16) a fin de obtener un promedio temporal nulo es necesario que (E_i) = 0 y (N_i) = 0 para todos los enteros positivos i.

Con estos resultados y aquellos de las ecuaciones (12), (13), (19) y (20), las ecuaciones de movimiento "efectivas" para las coordenadas lentas de posicion X(t) y del momentum desplazado Y(t) son:

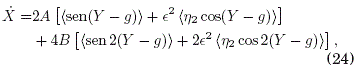
Ya que debemos integrar las ecuaciones para X(t) y Y(t) a fin de calcular el hamiltoniano efectivo H(X,Y), necesitamos entonces calcular las expresiones para los promedios temporales en X(t). Para ese propsito expresemos las siguientes funciones en forma de variable compleja:

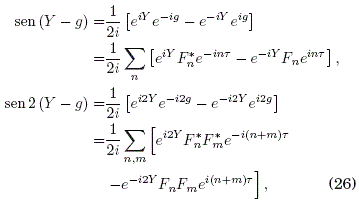
donde definimos

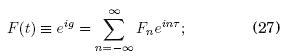
la expansión de Fourier de F(t) es posible ya que g(t) = es periódica para el campo real y periodico f(wt) = (con f^*_n = f_-n = f_n y f₀ = 0 ), así que F(t) tambien es periódica. Vale la pena dilucidar la relacion entre los coeficientes de Fourier F_n y f_n, ya que se usaran después. De las definiciones dadas anteriormente tenemos que

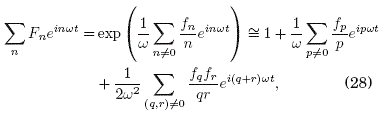
que se aproximo para w -> ∞.Ahora multiplicamos cada termino en (28) por (1/T)exp(-imwt) e integramos en t en el intervalo (0, T), as que se generan los trminos con la forma de

Así resulta que

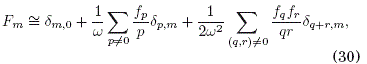
donde F^*_n= Fn. Para m = 0 obtenemos de (30):

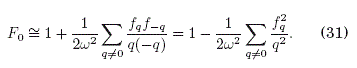
Este resultado ser de utilidad posteriormente.

Ahora continuamos calculando los promedios temporales en (26) para lo que usamos (29):

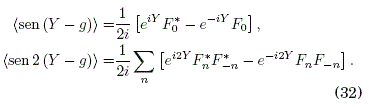
Sustituyendo (26) y (32) en la primera ecuación en (22) se obtiene una expresión para E₁ que está lista para ser integrada:

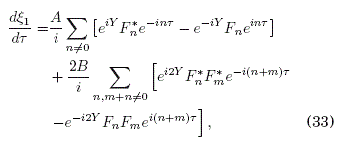
que conduce a

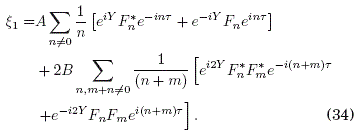
Este valor de E₁ se sustituye ahora en la segunda ecuacion en (23) y luego integramos la ecuación que resulta para N₂:

 

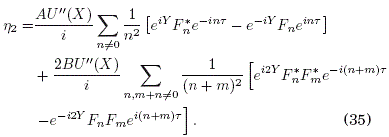
Con esta expresion para N₂, procedemos ahora de manera similar a calcular los demas promedios temporales de X(t) en (24). Los resultados son:

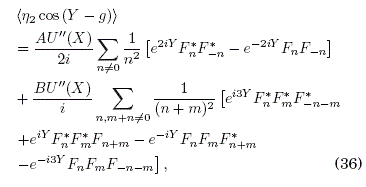
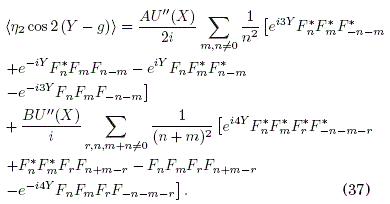
Con estos promedios temporales, y recordando que F_n = F^*_n, la expresión para X en (24) resulta:

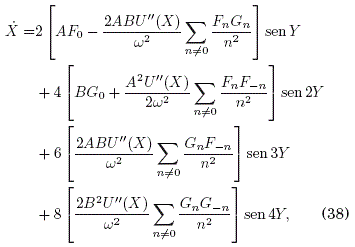
donde definimos Gm = A continuacion calculamos la ecuacion "efectiva" de movimiento (25) para el momento desplazado lento Y(t), donde el unico promedio temporal que se necesita es E₁²

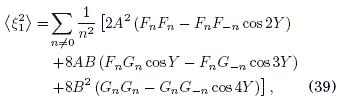
lo que conduce a

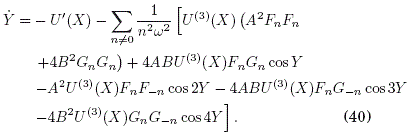
A fin de calcular el hamiltoniano efectivo H(X, Y) que debe representar la conservacion de la energía total, notemos que podemos construir esa funcion constante en las coordenadas lentas X, Y a partir de las relaciones (38) y (40) que calculamos antes: X/Y = dX/dY, de donde se obtiene -YdX + XdY = 0, y que conduce a una ecuacion diferencial exacta si -dY/dY = dX/dX; en efecto, esta condicion se cumple, como se verifica a continuacion:

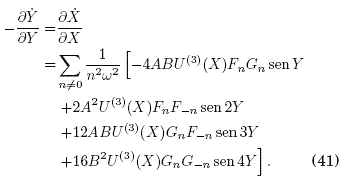
En este caso, dH(X, Y) = 0 para la funcion constante H(X, Y) que se calcula a partir de la teoría de ecuaciones diferenciales como de (38) y (40) este calculo es directo y conduce finalmente al hamiltoniano efectivo:

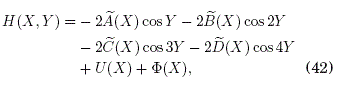
donde:

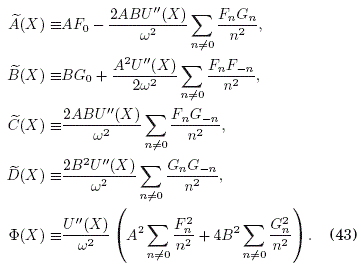
En esta expresion observamos los términos cuya dependencia funcional en X no supone un significado físico particular en la teoría de transporte de enlace fuerte; sin embargo, ya sea para un potencial estatico parabólico (U(X) = kX²/2) o lineal (U(X) = aX), esos terminos son elementos de hopping modificados o "reparametrizados", tales que cuando w->∞, y aparecen nuevos terminos o elementos de hopping "inducidos", , tales que cuando w -> ∞.

Los elementos de hopping efectivos en (43) se pueden reescribir de manera simplificada definiendo las cantidades adimensionales

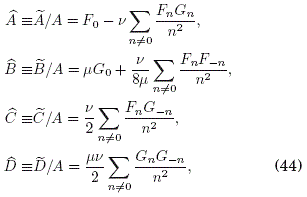
junto con los parametros de pequenez u = B/A (para A > B) y v = 4BU"(X)w^-2 (para w ->∞ ). El termino en (42) es una constante aditiva inmaterial que no conlleva algun efecto físico observable (para los potenciales estaticos parabólico o lineal) y puede ser ignorado de aquí en adelante.

 

3. INGENIERIA DE INTERACCIONES

Consideremos a continuacion el caso de un campo externo oscilante de la forma f(t) = 2f1 cos t + 2f2 cos 2t. Los coeficientes de Fourier correspondientes para la funcion periódica F(t) definida en (27) son Los elementos de hop-ping efectivos adimensionales que resultan son

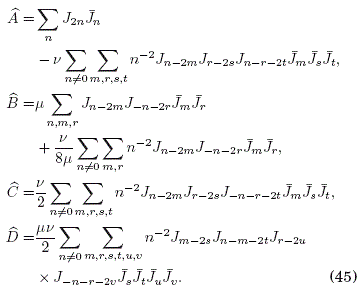
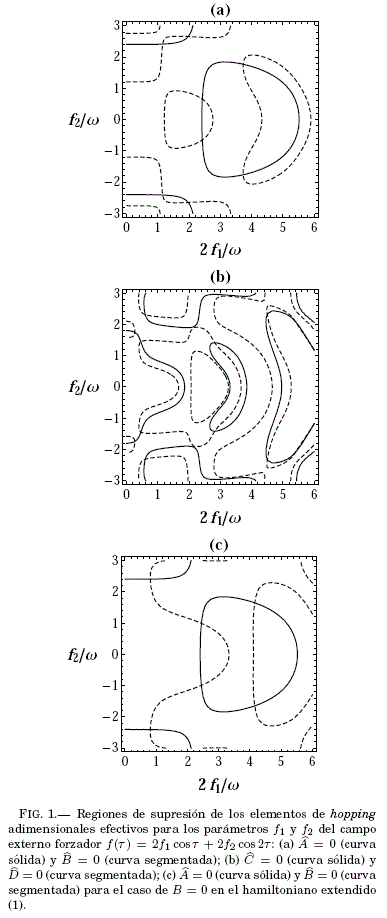
Controlando las intensidades 2f₁ y 2f₂ del campo externo f(t) en las funciones de Bessel en (45) es posible suprimir los valores de (ya sea de manera simultanea o por separado) asícomo . Esto se muestra de manera esquematica en la Fig.1: (a) caso de = 0 (curva solida) y = 0 (curva segmentada), (b) caso de = 0 (curva solida) y = 0 (curva segmentada). Para el caso de = 0 en (45) solo quedan los elementos efectivos adimensionales de hopping reparametrizado e inducido : =

la Fig.1(c) muestra los casos de = 0 (curva solida) y = 0 (curva segmentada). Esta figura coincide exactamente con la que reportan Itin & Katsnelson (2015) que fue obtenida con el formalismo cuantico. Para el caso del campo externo con la forma mas simple f(t) = 2f₁cos t, los elementos de hopping efectivos en (45) se simplifican como:

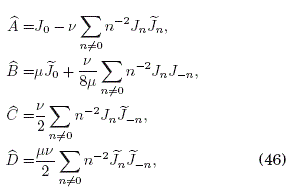
donde las funciones de doble argumento se obtuvieron aplicando la formula de duplicación para funciones de Bessel, a las expresiones en (43).

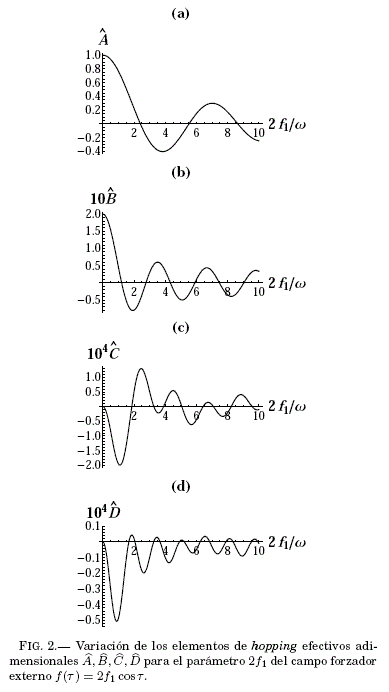
En la Fig.2 observamos la dependencia de los elementos de hopping en (46) en la intensidad 2f₁ del campo; en particular, observamos la supresion de los elementos de hopping, aunque no de manera simultanea, para valores específicos de 2f₁. De hecho, los ceros de en la Fig.2 corresponden a las intersecciones de ambas curvas, solida y segmentada, con la lınea horizontal f₂ = 0 en la Fig.1. Para el caso de B = 0, los unicos elementos de hopping efectivos adimensionales reparametrizados e inducidos son cuya dependencia en 2f₁ se grafica en la Fig.3.

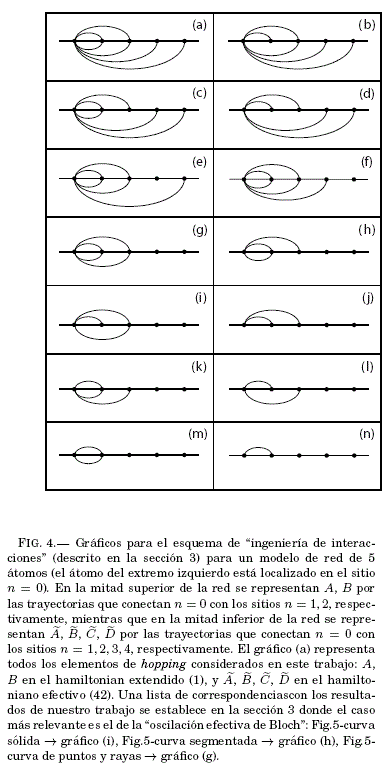
En la Fig.4 diseñamos 14 gráficos que proveen una ayuda visual para la "ingeniería de interacciones" descrita en esta seccion. La Fig.4(a) representa todos los elementos de hopping considerados en nuestro trabajo: A, B en el hamiltonian extendido (1) y en el hamiltonian efectivo (42). El modelo de red de la Fig.4 consiste de 5 atomos donde el átomo del extremo izquierdo esta localizado en el sitio n = 0. En la mitad superior de la red estan representados , por las trayectorias que conectan n = 0 con los sitios n = 1,2, respectivamente, mientras que en la mitad inferior de la red estan representados por las trayectorias que conectan n = 0 con los sitios n = 1,2,3,4, respectivamente. Ası, podemos establecer la siguiente lista de correspondencias:

Fig.1->Fig.4(a),
Fig. 1(a)-curva slida —> Fig.4(b),
Fig. 1(a)-curva segmentada —> Fig.4(c),
Fig.1(a)-puntos de interseccin —> Fig.4(d),
Fig. 1(b)-curva slida ->Fig.4(e),

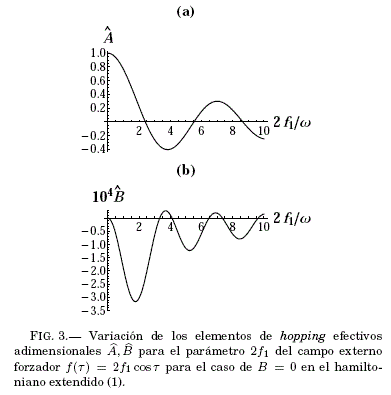
Fig. 1(b)-curva segmentada —> Fig.4(f),
Fig.1(b)-puntos de interseccin —> Fig.4(g),
Fig.1(c) ->Fig.4(k), Fig.1(c)-curva slida -> Fig.4(1),
Fig. 1(c)-curva segmentada —> Fig.4(m),
Fig.2 -> Fig.4(a),
Fig.2-puntos de cruce con el eje horizontal ->Fig.4(b, c, e, f),
Fig.3 -> Fig.4(k),
Fig.3(a)-puntos de cruce con el eje horizontal -> Fig.4(l),
Fig.3(b)-puntos de cruce con el eje horizontal —> Fig.4(m).

El caso mas sencillo y no trivial para el que podemos probar nuestros resultados y que tiene un significado intuitivo para la ingeniería de interacciones es la "oscilacion efectiva de Bloch", que corresponde a la combinacion de un campo externo estático lineal U(X) = aX y un campo forzador F(t) = 2f₁cos(t). En este caso se obtiene los elementos de hopping en (45) (con v = 0), y de aquí el hamiltoniano efectivo en (42). Las ecuaciones de movimiento (38) y (40) para X y Y son

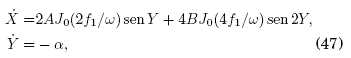
cuya solución es

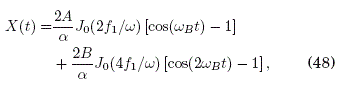
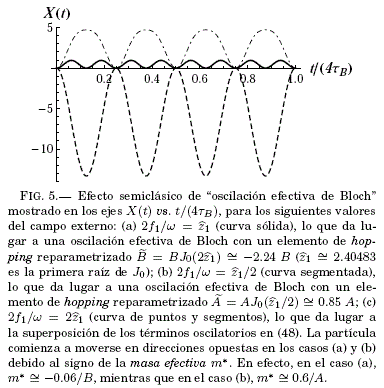
para las condiciones iniciales X(0) = Y (0) = 0 y con ω_B = 2π/τB ≡ |a| la frecuencia usual de la oscilacion de Bloch para el hamiltonian H(X, Y) = —2AcosY + aX. La Fig.5 muestra el grafico de X(t) vs. t/(4t_b) para los valores: (a) 2/f₁/w = (curva solida), (b) 2/f₁/w = /2 (curva segmentada) y (c) 2f₁/w = (curva de rayas y puntos); = 2.40483 es la primera raíz de J₀ En el caso (a) el primer termino de X(t) en (48) se anula y el segundo termino describe una oscilación de Bloch efectiva con un elemento hopping reparametrizado = BJ₀(2) -2.24 B; en el caso (b) el segundo termino de X(t) en (48) se anula y el primer termino describe una oscilacion de Bloch efectiva con un elemento de hopping reparametrizado = AJ₀(/2) = 0.85 A; en el caso (c) el movimiento resultante es una superposicion de los términos oscilatorios de (48). El movimiento en sentidos opuestos de los casos (a) y (b) se puede relacionar con la definicion de masa efectiva como m* = para la energía E(Y) asociada al hamiltoniano efectivo H(X, Y) (Ashcroft & Mermin 1976), que en este caso conduce a para Y = 0. En efecto, en el casa (a), , mientras que en el caso (b), , en consecuencia, la partícula comienza a moverse en direcciones opuestas. Las correspondencias en este caso de la "oscilacion de Bloch efectiva" son:

Fig.5-curva solida —> Fig.4(i),

Fig.5-curva segmentada —> Fig.4(h),

Fig.5-curva de puntos y segmentos —> Fig.4(g).

 

4. SIMULACIÓN NUMÉRICA CUÁNTICA

A continuacion usaremos la fórmula iterativa de evolucion temporal deducida a partir del algoritmo pseudo-espectral (Sanjines & Gallinar 2001)

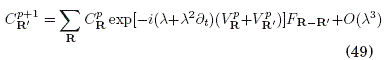
para los coeficientes de la expansion de la función de onda que se expresa en la base de funciones de Wannier de una banda y que estan centradas en torno al sitio de la red R: = Así, la solucion de (49) simula la evolución del paquete de ondas electronico en la red bajo la aproximación de una banda para el hamiltoniano de enlace fuerte H = T(p) + V(r,t), donde el operador de energía cinetica representa el salto (hopping) del electron entre los sitios de la red m y n, con elemento de hopping Amn; la energía potencial V(r, t) corresponde a las fuerzas externas que actuan sobre el electrón y es diferente del potencial periodico cristalino. En (49) usamos las definiciones: donde la integral se evalua en la primera zona de Brillouin (1 — BZ) con volumen v*.

Consideremos a continuacion el caso del hamiltoniano extendido (1) en una red unidimensional (constante de red a = 1) con interacciones a primeros y a segundos vecinos (los elementos de hopping correspondientes son A = A_n±1,n, B = A_n±2,n). A fin de estudiar la "oscilacion de Bloch efectiva" descrita en la Seccion 3, elijamos una energía potencial lineal U(x) = ax y un campo forzador armonico f/(wt) = 2f₁ cos(wt) con ; la integral Fn para el sitio R = n se evalua numéricamente para .

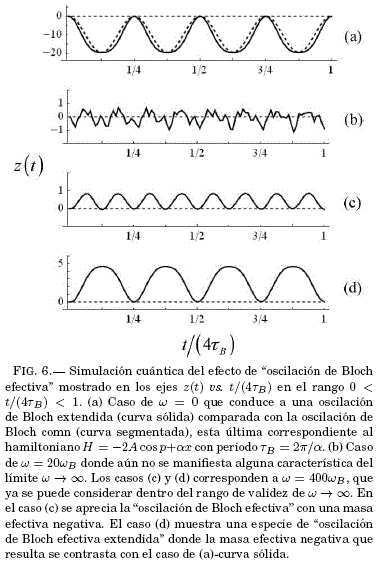
Una vez calculados los coeficientes Cn(t) procedemos a calcular el valor medio de la posicion en unidades de la constante de red: Cuando w = 0 obtenemos una especie de "oscilacion extendida de Bloch" que se muestra en la Fig.6(a)-curva solida y se compara con la oscilación de Bloch mostrada en la Fig.6(a)-curva segmentada (que se obtiene del hamiltoniano H = -2Acosp + ax) con periodo T_B = π/α; en todos los casos de la Fig.6 se muestra z(t) vs. t/(4T_B) de tal forma que 0 < t/(4T_B) < 1. La Fig.6(b) corresponde a w = 20w_B, el comportamiento dinamico de z(t) an no muestra alguna caracterıstica de las predicciones válidas para w->∞. Las Fig.6(c, d) corresponden a w = 400w_By se pueden considerar dentro del rango de validez de w->∞ , permitiendo así la comparacion directa entre el valor medio cuantico de la posición z(t) y la coordenada semiclasica de la posición lenta X(t) en (48); en efecto, en la Fig.6(c) se muestra la "oscilacion de Bloch efectiva" deducida del hamiltoniano efectivo Esto significa que la banda asociada a la interaccion a primeros vecinos se suprimio y sólo queda el efecto debido a la interaccion a segundos vecinos a través del elemento reparametrizado < 0 que corresponde a una masa efectiva negativa, provocando así el movimiento inicial en la direccion opuesta respecto a la oscilación de Bloch de la curva Fig.6(a)-segmentada; la línea horizontal segmentada representa el valor de referencia z(0) = 0. En la Fig.6(d) se tiene una especia de "oscilacion de Bloch efectiva extendida" análoga al caso de la Fig.6(a)-curva solida; los elementos efectivos de hooping reparametrizados son = AJ₀(2) =-0.24A y = BJ₀(4) = -0.21B, donde la masa efectiva negativa que resulta se puede contrastar con el caso de la Fig.6(a)-curva solida.

 

5. RESULTADOS Y DISCUSION

En este trabajo usamos un metodo inspirado en el metodo original desarrollado por Kapitza (1951) para calcular un hamiltoniano independiente del tiempo correspondiente al hamiltoniano extendido dado en (1). Este calculo se realizó usando el modelo semiclasico dado por las ecuaciones de movimiento de Hamilton para las coordenadas de posicion y momento. El resultado central de nuestro trabajo es la deduccion de la expresión (42) para el hamiltoniano efectivo H(X, Y) junto con el escenario para una "ingeniería de interacciones" propuesto en la seccion 3, en particular, para la supresión controlada de la interaccion a primeros vecinos que deja como efecto dominante la interaccion a segundos vecinos (Fig.1a). Proponemos como un efecto observable deducido de tal ingeniería de interacciones una "oscilacion efectiva de Bloch" con una masa efectiva resultante que es negativa para ciertos parametros del campo forzador externo (Fig.5); la validez y consistencia de este fenomeno se confirmó teóricamente usando el formalismo cuantico (sección 4).

La validez del resultado para H(X, Y) se puede comprobar sometiendolo a algunas pruebas;suponemos por simplicidad un campo forzador de la forma f/(T) = 2f₁ cos T pues, ademas, podemos así comparar nuestros resultados con los de otros trabajos. Una prueba trivial consiste de tomar el límite w->∞; en este caso podemos ver que los elementos de hopping y se eliminan, dando así por resultado el hamiltoniano (1) sin campo oscilatorio, como debe ser. Otra prueba consiste de tomar B = 0 en H(X, Y) para obtener

con elementos de hopping adimensionales Este resultado es interesante: el elemento de hopping inducido da cuenta de la interaccion a segundos vecinos que surge por el efecto combinado del campo rapidamente oscilante promediado y un potencial estatico no-uniforme, que en este caso es parabólico: Tal efecto fue reportado recientemente en (Itin & Neishtadt 2014; Itin & Katsnelson 2015) donde los autores usaron la misma tecnica de promediación temporal (como hicimos nosotros) aplicada a un hamiltoniano cuantico. Otra prueba consiste de elegir A = 0 en H(X, Y), lo que conduce a

con elementos de hopping adimensionales La comparacion de los hamiltonianos efectivos dados por (50) y (51) muestra que (51) se puede obtener de (50) duplicando el valor de la constante de red, a -> 2a (que elegimos como a = 1 en (1)); esta es una consecuencia directa de la simetría traslacional de la red infinita.

Para la ultima prueba extendemos el orden de la expansion en serie en (16) de manera consistente hasta E ⁴= w^-4; este es ciertamente un ejercicio algebraico tedioso, aun para el caso particular de B = 0. El resultado es

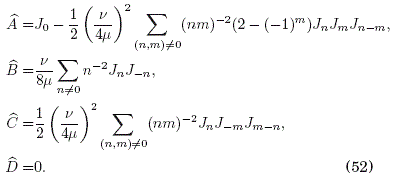
Podemos verificar la consistencia de (46) y (52) haciendo B = 0 en (46) y descartando los terminos del orden de E⁴ en (52); esto conduce a los resultados usuales: Como un resultado colateral para este caso, y a manera de una comprobacion cruzada de nuestros resultados, deducimos de (38) y (40) las ecuaciones de movimiento para X(t) y Y(t):

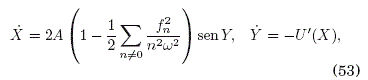
donde usamos el resultado dado en (31). Estas ecuaciones resultan ser iguales a las que reportan en Martínez et al. (2014), aunque sus resultados se obtuvieron sin invocar la transformacion del "momen-tum desplazado" dada por (4).

En este trabajo consideramos expansiones pertur-bativas hasta ordenes de E² y E⁴ a fin de obtener resultados consistentes. Una expansion sólo hasta el orden de E sería insuficiente, por ejemplo, en (31) donde F₀ es el factor responsable del colapso de la banda a primeros vecinos en (43) cuando se cumple la condicion de que 2/f₁/w sea igual a una raíz de J0 (regimen de localización dinámica). Como se puede verificar en (31), la expansion hasta E da F₀ = 1 lo que es incorrecto pues la banda nunca colapsaría, revelando así la necesidad de expandir las series al menos hasta E² para obtener resultados correctos. La insuficiencia de la expansion hasta e tambien esta referida en Longhi (2008) donde el formalismo cuantico también muestra la evidencia de resultados incorrectos para la dinamica de tunelamiento electronico en arreglos de pozos múltiples.

 

6. CONCLUSIONES Y PERSPECTIVAS

En este trabajo se dedujo, dentro de la aproximacion semiclásica, un hamiltoniano efectivo H(X,Y) correspondiente a una partıcula cargada que se mueve a saltos (hopping) en una red en presencia de una campo estatico arbitrario y un campo uniforme rapidamente oscilante. Nuestros resultados comprenden aquellos reportados recientemente por Itin & Neishtadt (2014) y Itin & Katsnelson (2015), que fueron calculados usando el formalismo cuantico; nuestros resultados también comprenden aquellos reportados en Martínez et al. (2014) para las ecuaciones semiclasicas de movimiento que describen el movimiento lento de las coordenadas de posicion y momentum desplazado, X y Y. Propusimos a manera de un resultado novedoso, la observacion de un efecto de "oscilacion efectiva de Bloch" que surge de la supresion controlada de la interacción a primeros vecinos y deja a la interaccion a segundos vecinos como un efecto dominante asociado a una partıcula de masa efectiva negativa para valores específicos del campo forzador. Debe mencionarse que en trabajos recientes (Reich et al. 2002; Kundu 2011; Wright et al. 2009; Kadirko et al. 2013) las interacciones de largo alcance en una red se consideran refinamientos perturbativos a la interaccion dominante a primeros vecinos. De manera notable, y en completo acuerdo con nuestros resultados, en Madison et al. (1998) se reporto la observación de la cuasi supresion de la banda a primeros vecinos en una red optica donde la supresión completa no se logra alcanzar debido a acoplamientos con vecinos distantes y a la presencia de varias bandas.

Como perspectivas interesantes de nuestro trabajo podemos mencionar: (i) La posibilidad de extender nuestros resultados para incluir los de Martınez et al. (2014) hasta el orden de O(w^-4), y así probar las similitudes entre el regimen del continuo y el regimen discreto de la red, que en Martínez et al. (2014) son referidos como un asunto aun desconocido. (ii) Una extension natural de nuestro trabajo es considerar un hamiltoniano extendido generalizado con una relacion de dispersión de la forma , pues se sabe que la incorporacion de interacciones de largo alcance en el hamiltoniano conduce a efectos interesantes como ser la supresion de los elementos efectivos de hop-ping para campos externos forzadores especıficos. (iii) El estudio de la "ingeniería de interacciones" mediante el control de parametros físicos tales como la forma del potencial estatico U(x) o la dependencia temporal del campo uniforme f(wt) en (1); encontramos en nuestro trabajo que dentro de la aproximacion de O(w^-2), la forma relevante del potencial estatico debe ser lineal (U(X) = aX) o parabolica (U(X) = kX²/2); sin embargo, es posible que refinando los resultados hasta el orden de O(w ^-n) para n > 2, el potencial estatico U(X) pueda depender de potencias mayores de X. (iv) Se debe investigar otras formas de campos externos forzadores f(t) con componentes de Fourier arbitrarias, en vista de que el campo con dos componentes f(t) = 2f₁ cos(t) + 2f₂ cos(2t) considerado en este trabajo conduce a efectos fısicos relevantes. (v) Sugerimos que un efecto fısico observable en el contexto de la ingeniería de interacciones es la "oscilacion de Bloch efectiva" (para un potencial estatico lineal) donde el comportamiento dinamico de la posición semiclásica X(t) y del correspondiente valor esperado cuantico hxit son identicos; el grado de coincidencia numérica entre esas dos coordenadas dinamicas para campos estaticos arbitrarios es un tema interesante por investigar.

 

AGRADECIMIENTOS

Agradecemos sinceramente a: Dr. Cesar Flores (IAI-UTA, Chile), Dr. Luis A. Martínez y Dr. Jean-Pierre Gallinar (USB, Venezuela) por las discusiones interesantes y estimulantes.

Conflicto de intereses

Los autores declaran que no hay conflicto de intereses con respecto a la publicación de éste documento.

 

Notas

1 Una justificacion concisa y pedagógica del modelo semiclásico aplicado a un potencial periodico general se puede encontrar, por ejemplo, en el cap. 12 de Ashcroft & Mermin (1976).

 

REFERENCIAS

Ashcroft N & Mermin N (1976), Solid State Physics (Holt, Rinehart and Winston) Bandyopadhyay M.         [ Links ] & Dattagupta S. (2008), Pramana J. Phys., 70:

Bouchard A. M. & Luban M. (1995), Phys. Rev. B, 52: 5105

Dreisow F., Bahat-Treidel O., Welt D. & Szameit A. (2011), Opt. Lett., 36: 2065

Dunlap D. H. & Kenkre V. M. (1986), Phys. Rev. B, 34: 3625

Itin A. P. & Katsnelson M. I. (2015), Phys. Rev. Lett., 115: 075301

Itin A. P. & Neishtadt A. (2014), Phys. Lett. A, 378: 822

Kadirko V., Ziegler K. & Kogan E. (2013), Graphene, 2: 97

Kapitza P. L. (1951), in Collected Papers of P L. Kapitza, ed. D. ter Haar (Zh. Eksp. Teor. Fiz.), 588

Kundu R. (2011), Mod. Phys. Lett. B, 25: 163

Landau L. D. & Lifschitz E. M. (1985), Mecánica (Reverte)

Lenz G. (1999), Phys. Rev. Lett., 83: 963

Longhi S. (2007), Phys. Rev. B, 76: 195119

—. (2008), Phys. Rev. B, 77: 195326

—. (2009), Laser & Photon. Rev., 3, 243

Longhi S., Marangoni M., Lobino M., Ramponi R., Laporta P. Cianci, E. & Foglietti V. (2006), Phys. Rev. Lett., 96: 243901

Longhi S., Dreisow F., Heinrich M., Pertsch T., Tunnermann A., Nolte S. & Szameit A. (2010) Phys. Rev. A, 82: 053813

Madison K. W., Fischer M. C., Diener R. B., Niu Q. & Raizen M. G. (1998), Phys. Rev. Lett., 23: 5093

Marte M. & Stenholm S. (1997), Phys. Rev. A, 56: 2940

Martınez L. A., Sanjinés D. & Gallinar J.-P. (2014), Int. J. Mod. Phys. B, 28: 1450173

Rahav S., Gilary I. & Fishman S. (2003), Phys. Rev. A, 68: 013820

Reich S., Maultzsch J., Thomsen C. & Ordejón R (2002), Phys. Rev. B, 66: 035412

Sanjines D. & Gallinar J.-P. (2001), Phys. Rev. B, 64: 054301

Wright A. R., Liu R & Zhang C. (2009), Nanotechnology, 20(40): 405203