Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de Medio Ambiente y Mineria
versión impresa ISSN 2519-5352
REV. MAMYM vol.8 no.1 Oruro jun. 2023
ARTÍCULOS ORIGINALES
Análise da estabilidade dos túneis com a teoria dos blocos
M.Sc. Ing. Rubén Medinaceli Tórrez
Ingeniero Civil e Ingeniero de Minas Carrera de Ingeniería de Minas, Petróleos y Geotecnia - Universidad Técnica de Oruro – Oruro – Bolivia.
Escola de Engenharia de São Carlos - Departamento de Geotecnia – Universidade de São Paulo - São Carlos – Brasil. ruben.medinaceli@usp.com
RESUMO.
Os túneis rodoviários são, sem dúvida, uma das obras de engenharia mais importantes, e é por isso que a segurança nesse tipo de obra é um tema que sempre deve ser considerado no projeto.
A engenharia de túneis requer um grande número de decisões no local, pois coletar dados para o projeto é muito complicado, uma vez que as características do maciço rochoso só podem ser vistas após o início dos trabalhos.
A direção do túnel é determinada antes de começar, e a teoria dos blocos de Goodman e Shi (1985) pode ser utilizada para identificar e analisar a existência ou não de blocos-chave nessa direção.
As galerias de mineração, ao contrário dos túneis rodoviários, não requerem revestimento como parte de seu reforço. Nesse caso, a teoria dos blocos desempenha um papel muito importante durante todo o processo de extração mineral. No entanto, quando algum tipo de revestimento é colocado por razões de estabilidade,
Nesta pesquisa, foi desenvolvida uma planilha do Excel com o objetivo de determinar quais desses blocos são blocos-chave que podem prejudicar a estabilidade do túnel ou da galeria de mineração.
RESUMEN.
Los túneles viales son sin duda una de las obras de ingeniería más importantes es por esto que la seguridad en este tipo de obras es un tema que siempre debe ser considerado en el diseño.
La ingeniería de túneles requiere un gran número de decisiones in situ, debido a que la toma de datos para el diseño es muy complicada, puesto de que se pueden ver las características del macizo rocoso recién una vez iniciados los trabajos.
La dirección del túnel es determinada antes de empezar el y la teoría de bloques de Goodman y Shi (1985) se puede utilizar para conocer y analizar la existencia o no de bloques clave en esta dirección.
Las galerías mineras a diferencia de los túneles viales no precisan de revestimiento como parte de su refuerzo. En este caso la teoría de bloques cumple un papel muy importante durante todo el proceso de extracción mineral; Sin embargo, cuando se coloca algún tipo de recubrimiento, por razones de estabilidad,
La presente investigación se desarrolla una planilla Excel con la finalidad de determinar cuáles de estos bloques son bloques calve que pueden perjudicar la estabilidad del túnel o galería minera.
1. ESTABILIDADE E CINEMÁTICA DE BLOCOS REMOVÍVEIS.
Alguns dos blocos criados pela interseção de descontinuidades e planos de escavação mostraram-se finitos e não intertravados. Esses blocos foram chamados de removíveis. Os blocos removíveis são divididos em 3 tipos de acordo com a teoria de blocos de Goodman e Shi (1985):
I. BLOCOS CHAVE; que se espera que se movimentem, quando a escavação estiver concluída, a menos que seja fornecido o suporte necessário.
II. BLOCOS CHAVE POTENCIAIS; que estejam em posição adequada para cair ou escorregar no momento da escavação; mas isso não acontecerá devido ao atrito disponível nas faces do bloco, que é suficiente para manter o bloco em estado de equilíbrio.
III. BLOCOS ESTÁVEIS; que não pode deslizar ou cair, mesmo quando o ângulo de atrito nas faces é zero, porque a orientação da força resultante promove a estabilidade.
Do exposto, conclui-se que apenas os blocos removíveis merecem uma análise de estabilidade.
Tendo identificado blocos removíveis como candidatos para análise detalhada, é conveniente classificar sua subdivisão em um dos dois tipos de análise possíveis disponíveis.
A primeira é uma análise de modo, que é realizada para distinguir blocos estáveis (Tipo II) de possíveis blocos chave ou verdadeiros blocos chave (Tipo II e I). A direção da força resultante deve ser especificada, mas não é necessário fornecer ou usar as propriedades das descontinuidades neste ponto da análise.
A segunda é uma análise de estabilidade, onde é necessário fornecer os ângulos de atrito para cada superfície de descontinuidade em contato, a fim de separar os blocos chave potenciais (II) e verdadeiros blocos chave (I). Os resultados da análise de modo orientam a análise de estabilidade.
a. MODOS DE DESLIZAMENTO.
Nesta seção, serão estabelecidas as relações existentes da direção da resultante de uma força sobre um bloco em estado incipiente de deslizamento e a direção de deslizamento. Juntamente com outras constantes cinemáticas e uma direção específica para a força resultante, essas regras nos permitirão estabelecer ¿qual, se houver, modo de escorregamento é aplicável a cada Joint Pyramid (pirâmide de juntas)? Goodman e Shi (1985)
Vamos denotar um bloco removível como Β . Ignorando a rotação, cada parte de Β experimenta um movimento descrito pelo mesmo vetor. O vetor unitário da direção de deslizamento será representado por ŝ . A discussão imaginará um estado de equilíbrio limite, em que o movimento ocorre sem aceleração.
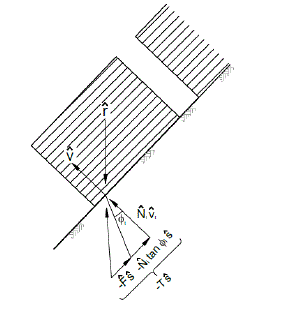
Sob um determinado conjunto de forças, não se pode esperar que Βesteja exatamente em uma condição de equilíbrio limite. Para ter Β em um estado limite, adicionaremos uma força fictícia -Fs, como mostrado na Figura 1. Quando F é positivo, o bloco tenderá a deslizar a menos que seja adicionado suporte artificial. No caso oposto, um valor negativo de F implica que o bloco Β está seguro contra o deslizamento. Portanto, F pode ser usado com um veículo para discutir condições limitantes. Goodman e Shi (1985)
Figura 1. Diagrama da força fictícia F e o valor da direção de deslizamento ![]()
Fonte: Block theory and its application to rock engineering - Goodman e Shi (1985)
Β = bloco removível
![]() = Vetor unitário da direção de deslizamento
= Vetor unitário da direção de deslizamento
F= Força fictícia
Φi =Atrito
r= Resultante de todas as outras forcas forças que atuam no bloco
i. FORÇAS ATUANDO EM B (Bloco removível)
Existem 3 contribuições para as forças que atuam no bloco Β e são elas:
1. A resultante (N) dos componentes normais correspondentes às reações nos planos de deslizamento. Onde ![]() é o vetor unitário normal ao plano de descontinuidade l, direcionado ao bloco Β; então as reações normais são:
é o vetor unitário normal ao plano de descontinuidade l, direcionado ao bloco Β; então as reações normais são:
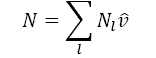
Assume-se que nãohá forças de tração ao longo da descontinuidade, por tanto, N ≥0
2. A resultante T das forças de atrito tangenciais é: Tl= N l tan Φl e a resultante disso e a força fictícia é:
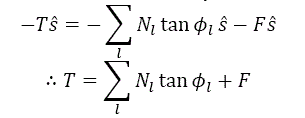
Para um bloco chave potencial ou verdadeiro, por projeto, o deslizamento ocorrerá se Φl = 0, porque um valor positivo de F implica em deslizamento, T ≥ 0
3. A resultante r de todas as outras forças que atuam no bloco Β, incluindo peso, forças de infiltração ou pressão hidráulica externa, forças de inércia e cargas ou forças de suporte. A força r será denominada como: Resultante Ativo.
A condição de equilíbrio para bloco chave potencial ou verdadeiro Β é:
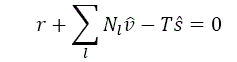
Com
![]() 0
0
Pelo Teorema da Remobilidade Goodman e Shi (1985), a direção de deslizamento ![]() do bloco removível Β pertence ao JP (Pirâmide de junta) do bloco B; quer dizer:
do bloco removível Β pertence ao JP (Pirâmide de junta) do bloco B; quer dizer: ![]()
Os termos usados na teoría de blocos de Goodman e Shi (1985) foram mantidos em inglês
ii. ELEVAÇÃO (Lifting)
A Figura 2 mostra um bloco chave movendo-se livremente de seu local original. Chamaremos esse fenômeno de elevação, porque nenhum plano de descontinuidade permanece em contato, ![]() não pode estar contido em nenhum plano de descontinuidade. Porque nenhuma descontinuidade está em contato,
não pode estar contido em nenhum plano de descontinuidade. Porque nenhuma descontinuidade está em contato, ![]() torna-se:
torna-se: ![]()
Para um bloco chave verdadeiro ou potencial, T ≥ 0, portanto:![]()
Os JP foram definidos como conjuntos fechados, isto significa que o JP inclui não apenas o espaço dentro da pirâmide, mas também as faces laterais e as arestas. A condição para elevação é que ele ![]() deve estar contido dentro do JP, mas não em seus limites.
deve estar contido dentro do JP, mas não em seus limites.
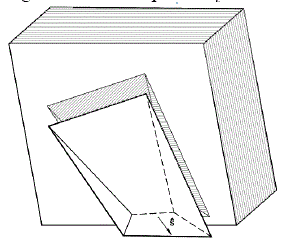
Figura 2. Elevação ou desprendimento de um bloco (lifting)
Fonte: Block theory and its application to rock engineering - Goodman e Shi (1985)
PROPOSIÇÃO DE ELEVAÇÃO. Sim ![]() não é paralelo a nenhum plano do JP, a condição necessária suficiente de Β, para satisfazer a equação de equilíbrio é que:
não é paralelo a nenhum plano do JP, a condição necessária suficiente de Β, para satisfazer a equação de equilíbrio é que: ![]()
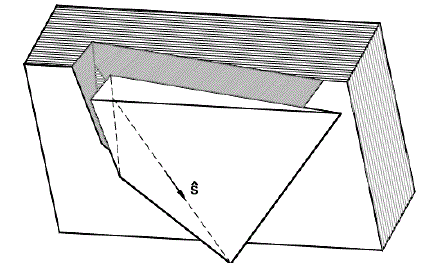
iii. DESLIZAMENTO EM UMA FACE.
A Figura 3 mostra o exemplo de um bloco deslizando ao longo de uma de suas faces, neste caso, ![]() é paralelo a apenas um plano de Β (plano i) e a direção de deslizamento
é paralelo a apenas um plano de Β (plano i) e a direção de deslizamento ![]() é a projeção ortográfica de r sobre o plano i.
é a projeção ortográfica de r sobre o plano i.
![]()
Onde
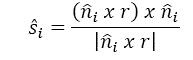
Onde: ![]() é o vetor normal direcionado para cima ao plano i, determinado por:
é o vetor normal direcionado para cima ao plano i, determinado por:
![]() =(A,B,C)=(sin α sin Β, sin α cos Β, cos α) N este caso, todos os planos de descontinuidades, exceto o plano i, abrirão e
=(A,B,C)=(sin α sin Β, sin α cos Β, cos α) N este caso, todos os planos de descontinuidades, exceto o plano i, abrirão e ![]() , onde Pi ;representa o plano i. Goodman e Shi (1985)
, onde Pi ;representa o plano i. Goodman e Shi (1985)
PROPOSIÇÃO DE DESLIZAMENTO EM UMA FACE. Se a direção de deslizamento ![]() encontra-se em um único plano, Pi , a condição suficiente e necessária que o bloco removível Β deve satisfazer a equação de equilíbrio
encontra-se em um único plano, Pi , a condição suficiente e necessária que o bloco removível Β deve satisfazer a equação de equilíbrio
![]() , è
, è ![]() e
e ![]() onde
onde ![]() é a projeção ortográfica de r no plano Pi
é a projeção ortográfica de r no plano Pi
Figura 3. Deslizar em uma face ou superfície deslizante
Fonte: Block theory and its application to rock engineering - Goodman e Shi (1985)
iv. DESLIZAMENTO EM DUAS FACES.
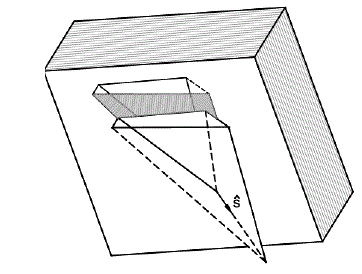
As Figuras 4 e 5 mostram exemplos de blocos deslizando ao longo de dois planos, Pi e Pj (ou ao longo de sua linha de interseção), porque é a única direção comum de ambos os planos. A direção de deslizamento ![]() é a direção ao longo da linha de interseção que faz um ângulo agudo com a direção da resultante ativa (resultante de todas as forças envolvidas).
é a direção ao longo da linha de interseção que faz um ângulo agudo com a direção da resultante ativa (resultante de todas as forças envolvidas).
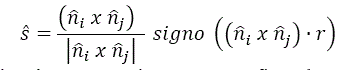
Além disso, a direção de deslizamento é uma aresta do JP formada pela interseção dos planos i e j: Goodman e Shi (1985) ![]()
PROPOSIÇÃO DE DESLIZAMENTO EM DUAS FACES. Se a direção de deslizamento é simultânea em dois planos, Pi e Pj ; as condições suficientes e mínimas para que o bloco Β satisfaça a equação de equilíbrio
![]() são:
são: ![]()
e
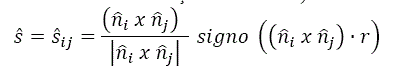
Onde ![]() e
e ![]() são as projeções ortográficas de r sobre os planos Pi e Pj ;, respectivamente, conforme indicado em a equação
são as projeções ortográficas de r sobre os planos Pi e Pj ;, respectivamente, conforme indicado em a equação ![]()
Figura 4. Deslizando em dois planos Fonte: Block theory and its application to rock
engineering - Goodman e Shi (1985)
Figura 5. Deslizando em dois planos Fonte: Block theory and its application to rock
engineering - Goodman e Shi (1985)
b. A FORÇA DE DESLIZAMENTO
As equações de equilíbrio para translação livre, deslizamento em uma ou duas faces, têm dado na seção anterior. Usando essas equações, podemos calcular as equações correspondentes para a força de escorregamento F ![]() .
.
ELEVAÇÃO (Lifting)
Neste caso, ![]() = 0, para todos os planos de descontinuidades e a equação
= 0, para todos os planos de descontinuidades e a equação ![]() , torna-se: F=T e a equação de equilíbrio é:
, torna-se: F=T e a equação de equilíbrio é:![]() e a combinação comF=T, resulta em:
e a combinação comF=T, resulta em: ![]() |
|
Quando a gravidade é o único contribuinte para a resultante ativa, F é simplesmente o peso do bloco. Goodman e Shi (1985)
DESLIZAMENTO EM UMA FACE.
Como há apenas um plano de contato, a equação ![]() se torna
se torna

Substituindo esses dois últimos em ![]() temos:
temos: ![]() Onde
Onde ![]()
Pela declaração de deslizamento unilateral:![]()
Substituindo ![]() em
em ![]() , temos:
, temos:![]()
Esta fórmula é usada para obter a força de deslizamento em uma única face ao longo do plano Pi. Quando a resultante ativa r é dada apenas pela gravidade. r = (0,0,−W) Onde: W > 0 Suponha que a direção de mergulho e mergulho do plano Pi. sejam αi. e Βi. , respectivamente.
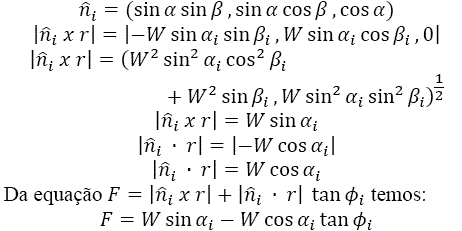
Esta equação expressa a Força de Deslizamento quando a resultante ativa r é devida unicamente à ação da gravidade. Goodman e Shi (1985)
DESLIZAMENTO EM DUAS FACES
Neste caso, o bloco removível Β, desliza ao longo dos planos do conjunto de descontinuidades i e j, os demais planos de descontinuidade são abertos. A força de reação normal ![]() = 0 para todo l ≠ i ou j, e
= 0 para todo l ≠ i ou j, e ![]() , torna-se:
, torna-se:
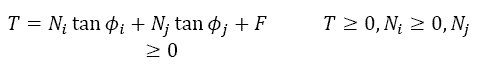
Pelo que:
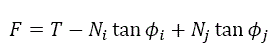
Sim: ![]()
Se obtem: 
Porque N ≥ 0, pode ser escrito como: 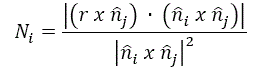
Similarmente 
Da equação a seguir temos: ![]() T=r*
T=r*![]()
Para um bloco chave ou bloco chave potencial, T > 0, então:
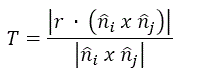
Substituindo:
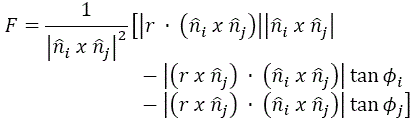
Esta equação fornece a força de deslizamento para um bloco chave ou bloco chave potencial, deslizando nos planos Pi e Pj . Goodman e Shi (1985)
CONDIÇÕES CINEMÁTICAS PARA ELEVAÇÃO E DESLIZAMENTO.
Nesta seção será comprovado que existe um JP correspondente a uma determinada direção de deslizamentoe então serão estabelecidosprocedimentos para identificálo. Uma análise de modo determina uma lista completa de JP's correspondentes a todas as direções de deslizamento. Isso será verificado nas seções subsequentes.
Lista completa de direções de deslizamento, dada uma força resultante r.
· Para elevação:![]()
Para deslizamento em uma face (i), as direções de deslizamento ![]() são determinadas por:
são determinadas por: 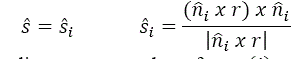
· Para deslizamento em duas faces (i) e (j) , as direções de deslizamento ![]()
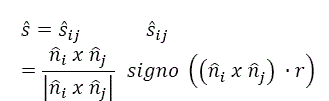
De acordo com a definição de “remobilidade”, cada bloco removível tem uma direção de deslizamento ao longo da qual pode ser movido sem colidir com o maciço rochoso adjacente. Então segue que: Goodman e Shi (1985)![]()
Levantamento
Quando um bloco é levantado, ![]() não é paralelo a nenhum plano P i . Assim, como
não é paralelo a nenhum plano P i . Assim, como ![]() é a normal direcionada ao bloco, para cada plano l do bloco.
é a normal direcionada ao bloco, para cada plano l do bloco. ![]()
Deslizamento em uma face
Para o caso de um deslizamento no plano Pi , ![]() é paralelo a Pi . Portanto, com
é paralelo a Pi . Portanto, com ![]() e a proposição de deslizamento em uma face, obtemos:
e a proposição de deslizamento em uma face, obtemos: 
Deslizamento em duas faces.
Para deslizamento nos planos i e j![]() . é paralelo aos planos i e j. Usando
. é paralelo aos planos i e j. Usando ![]() e a proposição de deslizamento em duas faces, obtemos:
e a proposição de deslizamento em duas faces, obtemos: 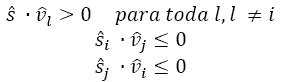
Conhecendo ![]() e r, essas equações fornecem informações suficientes para identificar todas as correspondentes
e r, essas equações fornecem informações suficientes para identificar todas as correspondentes ![]() , portanto, identificar o JP.
, portanto, identificar o JP.
c. ENCONTRAR A DIREÇÃODO DESLIZAMENTO PARAUM DETERMINADO JOIN0T PYRAMID (JP).
Apenas alguns JP 's têm uma direção de deslizamento. Aqueles JP 's que são removíveis, mas não possuem direção de deslizamento, são chamados de blocos estáveis, tipo III. Na próxima seção, será estabelecido um critério para que um bloco removível seja estável.
O vetor mais próximo de um JP em relação a r Dada a força resultante r e um JP (Pirâmide de junta), para qualquer vetor ![]() denotaremos como
denotaremos como ![]() o ângulo entre
o ângulo entre ![]() Se houver um vetor
Se houver um vetor ![]() tal que
tal que ![]() seja menor ou igual ao ângulo entre JP e
seja menor ou igual ao ângulo entre JP e ![]() qualquer vetor JP , então a
qualquer vetor JP , então a ![]() será chamado de "o vetor mais próximo de um JP a
será chamado de "o vetor mais próximo de um JP a ![]() O ângulo será
O ângulo será ![]() então chamado, “o menor ângulo entre JP e
então chamado, “o menor ângulo entre JP e ![]() . Goodman e Shi (1985)
. Goodman e Shi (1985)
As trêsproposiçõesa seguirdeterminamos vetores mais próximos dos JP 's para todos os casos
· Proposição 1:
Se existe um vetor![]() , tal que
, tal que ![]() < 90°, então existe um e somente um vetor mais próximo de JP em relação a r.
< 90°, então existe um e somente um vetor mais próximo de JP em relação a r.
· Proposição 2:
Se 𝑠 é a direção de escorregamento de JP sob a resultante ativa r, então ![]() é o vetor mais próximo de JP em relação a
é o vetor mais próximo de JP em relação a ![]()
· Proposição 3:
Si ![]() é o vetor mais próximo de JP em relação a r, e
é o vetor mais próximo de JP em relação a r, e ![]() ̂ ∙
̂ ∙![]() > 0, portanto,
> 0, portanto, ![]() ̂ é a direção de deslizamento (
̂ é a direção de deslizamento (![]() =
= ![]() ).
).
Critérios para blocos estáveis.
Essas proposições geram critérios para julgar se um JP corresponde ou não a um bloco estável.
Critério 1: Um JP corresponde a um bloco estável se para qualquer ![]()
![]()
Critério 2: Um JP corresponde a um bloco estável se r,![]() e
e ![]() todos não estiverem contidos no JP
todos não estiverem contidos no JP
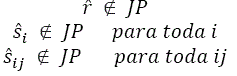 .
.
d. TEOREMA DO EIXO DO TÚNEL.
Um teorema sobre as relações entre o eixo do cilindro do túnel e as pirâmides de juntas ( JP´s) dos blocos removíveis provará ser muito útil, dito teorema diz:
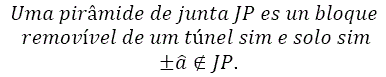
Se o eixo do túnel ![]() um elemento do JP, o teorema dita que o JP não pertence a nenhum bloco removível do tunel. Isso porque o eixo do tunel pertence a cada um dos semiespaços cuja união determina a pirâmide de escavação EP (Excavation Pyramid) e, portanto, EP ∩ JP deve conter
um elemento do JP, o teorema dita que o JP não pertence a nenhum bloco removível do tunel. Isso porque o eixo do tunel pertence a cada um dos semiespaços cuja união determina a pirâmide de escavação EP (Excavation Pyramid) e, portanto, EP ∩ JP deve conter ![]() e de acordo com isso, não está vazio. Cada JP que não contém o eixo do túnel possui um bloco removível correspondente no túnel. Goodman e Shi (1985)
e de acordo com isso, não está vazio. Cada JP que não contém o eixo do túnel possui um bloco removível correspondente no túnel. Goodman e Shi (1985)
2. PROGRAMA EXCEL.
Toda essa metodologia foi inserida em uma planilha do Excel para poder fazer uma análise de estabilidade muito mais rápida, e não ter que realizar cálculos longos.
a. SOBRE A PLANILHA
- A planilha está em espanhol.
- É necessário o conhecimento da teoria de blocos de Goodman e Shi (1985)
- A planilha exige que sejam registrados os dados de mergulho e direção de mergulho de 3 famílias de descontinuidades; se houver 4 ou mais, devem ser feitas combinações de três.
- É necessário anotar a direção do eixo do túnel, por enquanto o mergulho doTúnel permanece em 0°, mas em uma versão futura do programa isso pode mudar.
- Uma vez inseridos esses dados, o programa calcula automaticamente e exibe como resultado e um gráfico dos grandes círculos das famílias de descontinuidades e da superfície de escavação para análise posterior.
- O programa calcula a direção, modo y força de deslizamento de todas as pirâmides de juntas, mas com o método estereográfico é possível analisar a posição de cada bloco em relação ao teto, superfície e piso do túnel.
Na Figura 6 você pode ver o programa com o exemplo visto no estudo de caso.
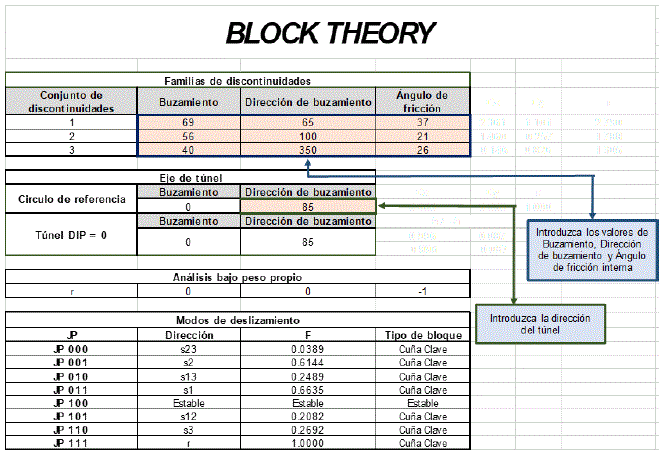
Figura 6. Estudo de caso - 2 - Programa Excel
3. ESTUDO DE CASO
Neste estudo de caso tem os seguintes dados:
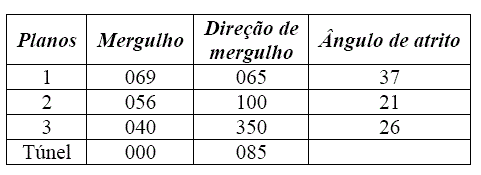
a. ANÁLISE DOS RESULTADOS.
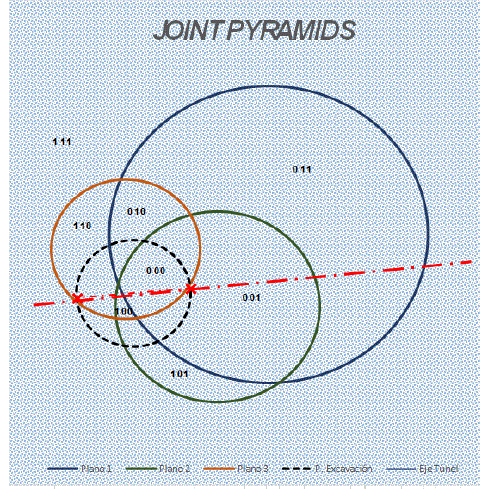
Blocos estáveis: Na figura 6 você pode ver que a pirâmide de junta (JP) 100 é um bloco estável, é um bloco de piso, então ele não pode deslizar sob seu próprio peso, na a tabela reflete essa situação.
Eixo de túnel: Devido ao teorema do eixo do túnel, as pirâmides de juntas (JP) 110 e (JP) 001 são blocos estáveis.
Bloco chave: Os outros blocos são:
- A pirâmide de junta (JP) 110 é um bloco na parede direita.
- As pirâmides de juntas (JP) 011 e (JP) 111 são blocos no teto do túnel.
- A pirâmide de junta (JP) 101 é um bloco na parede esquerda.
Como pode ser visto, este programa nos ajuda a realizar análises de estabilidade com teoria de blocos proposta por Goodman e Shi, muito rapidamente, os blocos chave e sua localização podem ser identificados.
4. CONCLUSÕES
·A teoria dos blocos proposta por Goodman e Shi ajuda a identificar os blocos instáveis no túnel, também ajuda a identificar onde esses blocos se encontram na seção do túnel.
·A partir de uma planilha do Excel, os testes de variação de mergulho e direção de mergulho podem ser realizados e ver se novos blocos chave são criados.
·A implementação desta planilha é uma ferramenta muito útil para o engenheiro responsável pelo projeto do túnel identificar rapidamente os principais blocos chave.
Este modelo também pode ser usado em escavações de mineração.
Bibliografia
Goodman R & Shi G (1985). Block theory and is application to rock engineering. Prentice Hall. Ayes JC (2011). La teoría de bloques aplicada a la mecánica de rocas. Instituto Politécnico Nacional. [ Links ] [ Links ]
Huang T, Chen J, Chang C (2003). Stability analysis of rock slopes using block theory. Journal of the Chinese institute of engineers. [ Links ]
Zheng J, Kulatilake P, Shu B, Sherizadeh T, Deng J (2014). Probabilistic block theory analysis for a rock slope at an open pit mine. Computers and geotecgnics. [ Links ]
T. Liu, J. Deng, J. Zheng, L. Zheng, Z. Zhang, H.Zheng (2016). A new semi-deterministic block theory method with digital photogrammetry for stability analysis of a high rock slope in China. Engineering geology [ Links ]
Javier, A. (s.f.). Problemas de mecánica de rocas. Madrid: Bubok Publishing S.L. [ Links ]
Roberto Tomás Jover (1), I. F. (2002). APLICACIONES DE LA PROYECCIÓN ESTEREOGRÁFICA. XIV Congreso Internacional de Ingeniería Gráfica. [ Links ]
Artículo recibido: 29.04.2023
Artículo aceptado: 28.05.2023