Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de Medio Ambiente y Mineria
versión impresa ISSN 2519-5352
REV. MAMYM v.5 n.2 Oruro dic. 2020
ARTÍCULOS
Optimal recovery of manganese ore in room and pillar mining using
3D numerical analysis
Recuperación óptima de menas de manganeso por cámaras y pilares
usando análisis numérico en 3D
Vidal Felix Navarro Torres
Instituo Tecnológico VALE, Brazil
vidal.torres@itv.org
Artículo recibido en: 30-09-2020 Artículo aceptado: 23-10-2020
Abstract
In the room and pillar method, maximum ore recovery obtained by the acceptable safety factor, compatible of the depth, geometry of the room and pillars, the goemechanical rock mass properties surrounding mining opening and overlying area. Although traditional methods allow some support, but do not allow an exhaustive interpretation and optimum design. For this reason, we have adopted the 3D numerical model and calibrate by in situ database for obtain the optimal geometry that allows to get the maximum ore recovery compatible of acceptable safety factor. The case study corresponds to the manganese room and pillar Brazilian Urucum mine, which allowed for a 44% to 80% o re recovery.
Keywords: room and pillar, maximum ore recovery, acceptable safety factor
Resumen
En el método de cámara y pilares, la máxima recuperación de mineral es obtenida para un factor de seguridad aceptable, compatible con la profundidad, geometría de las cámaras y pilares, las propiedades goemecánicas del macizo rocoso que rodean la zona de explotación minera y el área supra yacente. Aunque los métodos tradicionales permiten cierto apoyo, no permiten una interpretación exhaustiva y un diseño óptimo. Por este motivo, fue adoptado el modelo numérico 3D y calibrado mediante base de datos in situ para obtener la geometría óptima que permita obtener la máxima recuperación de mineral compatible con un factor de seguridad aceptable. El caso de estudio corresponde a la mina brasileña que usa cámaras y pilares de la mina de manganeso de Urucum, que permitió una recuperación de mineral de 88% cuando inicialmente era de 44%.
Palabras clave: Cámaras y pilares, recuperación máxima, factor de seguridad aceptable
1. Introduction
The present article is the result of a study based on the observation of the room and pillar underground mining method atthe Urucum Manganese mine. The room and pillar method at Urucum mine works with rooms of 5 m x 11 m x 3.5 m and pillars of11mx11mx3.5m, allowing an ore recovery of 44% and remaining 56% at the mine site. The high content of non-recovered ore related to the rock mass quality, allows to assume that it is possible to apply an improvement on the pillar cut to maximize the ore recovery, but also assuring the underground mine stability. To achieve that, the following method is considered:
Geomechanic characterization of the rock mass located near the underground mining front areas of Urucum mine;
Geometric parameters characterization from the room and pillar applied at Urucum mine;
3D modeling of the geomechanic behavior from Urucum mine rock mass, for the underground opening stability analysis;
Maximize ore recovery achieving also mine global stability (applying FLAC 3D Security Factor) and roof & floor convergence (maximum displacement).
According to Zipf (2001), if the pressure applied over a pillar exceeds the pillar resistance, the tension over that pillar will be transmitted to the neighbor pillars. The additional tension over the neighbor pillars may overcame on the collapse of those pillars and by that, the collapse of large underground mining areas, becoming the main reason for applying the correct dimension when planning the mine pillars.
One of the most applied dimensioning methods for room and pillar is the influence area method, which considers dimensioning the pillar size due to the vertical applied tension over that pillar area of influence, and then it compare the applied tension to the pillar compression resistance.
Although, the orientation for existing discontinuities are not considered, which can affect the tension distribution.
The pillar resistance is determined by an general expression Equation (1) due to the resistance of the pillar rock mass Rrp, pillar width Sp, pillar height h, and numerical values from the adjustment of empirical data a, b, c, d.

On the other hand, the tension over the squared section pillar is determined by Equation (2), based on the rock mass average specific weight (γ) associated to the litostatic column which correspond to the influence area, mine depth (H) and room width (c).

The safety factor (SF) can be measured based on the pillar resistance, σp, and the tension over the pillar, Pp, which can be expressed by Equation (3) (Navarro Torres VF, et al, 2011).
![]()
For the applied methodology the recomended SF value is of 1.5 for short term pillars and 2.0 for long term pillars (Kuhnhein G, 2004 e Hoch T, 1991).
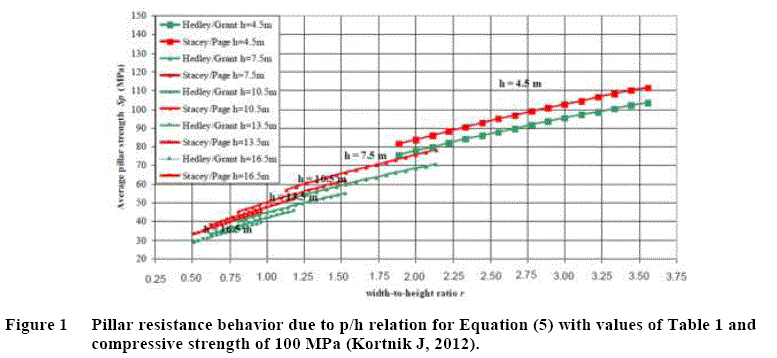
Most of the empirical studies of this area deals with coalmines, like the case of Over & Duvall, 1967, Bieniewaski, 1975, Salomon &Munro, 1967, Sheorey, 1987; para lavra de calcário, Krauland & Soder, 1987, Sjoberg, 1992. Para mármore e quartzito, Hedley & Grant, 1972, e González, 2006 cited by Verma AK, 2014).
For metallic ore mines, there are just a few studies, where the most known is the work of Lunder PJ et al 1994, observed by Equation (4).
![]()
Where: σc is the uniaxial compressive strength of intact rock
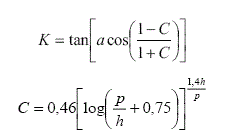
For Sp determination, Equation (5) can be used based on the rock mass simple compressive strength, σc (HoekeBrown, 1997).

Applying Equation (5) on a quartzite pillar in a determined case, c and d values can be resulted as presented at Table 1.
By simulating Equation (5) with Table 1 values (Figure 1), it is possible to observe that the higher is p/h relation, the higher will be the pillar resistance.
At Urucum mine, laboratorial studies made with manganese samples (Ayres da Silva L, 1989) allowed to obtain Equation (6):
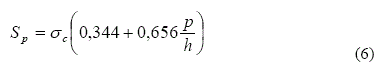
The application of numerical methods for evaluating underground mines is a useful tool, which allows estimating tension field changes, deformations and displacements that can be presented at the rock body due the mining activities. With the estimative is possible to evaluate local mining conditions, allowing increasing the pillar recovery, according to the estimative results.
According to Brandani (2011), the main goals of pillar modeling numerical methods are:
Obtaining an estimative for the loading capacity orthe maximum admissible loading;
Establishing appropriate geometric configuration to the estimated tension field;
Determining breakage module;
Rock mass properties retro-analysis based on the instrument data.
Nevertheless, when applying numerical analysis methods, there is just a few studies for metallic mines and insufficient data for manganese ore, as the available studies are related mostly to coalmines and for some limestone underground mines.
Recently, numerical methods that allows to analyses and optimize ore recovery have been use, as can be quoted Brandani (2011) study, where it compares numerical and traditional methods for determining the ideal size for pillars in an underground gold mine at Crixás/Brazil. Other methods can be seen at the research made on a tungsten mine at Penasqueira/Portugal using the FLAC3D software (Navarro Torres VF, et al, 2011).
The parameters studied at Brandani (2011) work, could prevent the evaluation of different dimensions as the tests conditions for the model to be run:
Pillar dimension 3 mx 3 m, 5 mx 5 m, 7mx 7 m;
Room dimension 6 mx 6 m, 8 mx 8 m, e 10 mx
10 m; Inferior ore body pillars with 4 mx 4 m dimensions and 5 m height (w/h = 0.8).
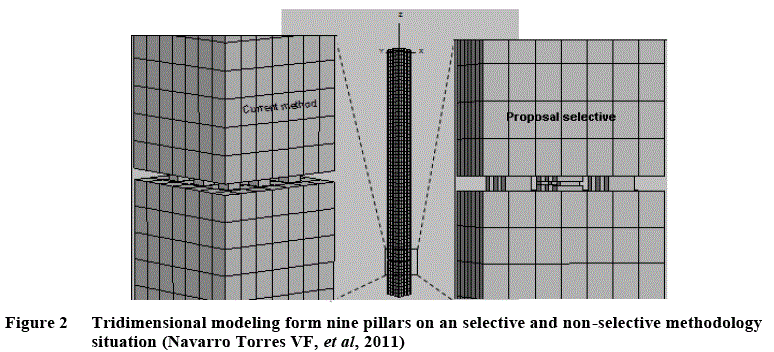
The work done at the Tungsten mine in Penasqueira/Portugal (Navarro Torres VF et al, 2011), analyzed the3mx3mx2m pillars stability with an 5 m room width. Over there was a schist ore body with pillars where it could be found quartz veins of 0.5 m width, disseminated with wolframite, 0.75 m schist layer on the superior and inferior part of the pillars, as also a selective cut on the central part of the quartz veins. Over there was also a 4 m x 4 m pillars with the same selective cut at the quartz veins, but in addition a 0.5 m width and height selective cut on the superior and inferior part of the pillar, as can be seen on Figure 2, which shows a tridimensional model made of 3,448 elements.
By the 3D modeling it was possible to analyze the distribution tension and the vertical and horizontal displacements with a high detail (Figure 3), which allowed to describe the situation over the pillars and rooms.
2 Methodology
2.1 Ore recovery
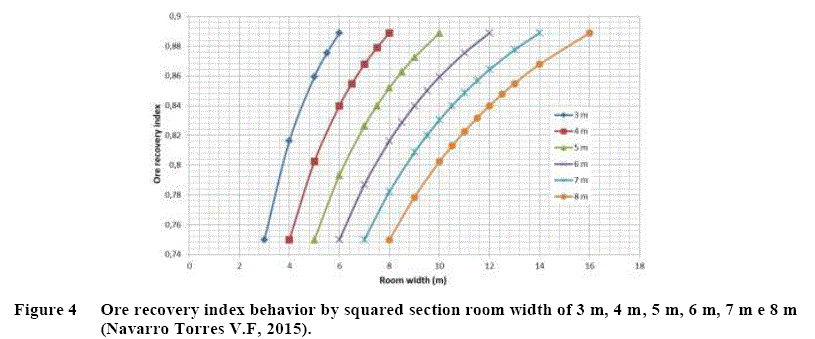
In Room & Pillar mining method when considering a square section pillar and a mining height equivalent to the ore body height, as can be seen at the second Manganese seam at Urucum mine. The ore recovery can be expressed by the recovery index described by Equation (7) (Navarro Torres VF, et al, 2011), considering the pillar and room width, p and c respectively.

Equation (7) is a geometric based method (Navarro Torres V.F, 2015), but it offers an important representation (Figure 4) as it is possible to achieve a recovery index. As for example, an index of 0.86 is possible to achieve with a pillar width of 3 m, 4 m, 5 m, 6 m, 7 m, 8 m and a respectively room width of 5 m, 6.6 m, 8.2 m, 10 m, 11.1 m and 13.2 m.
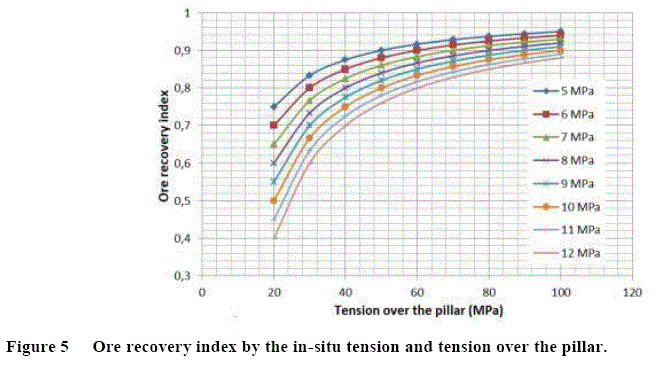
The recovery index can be expressed by Equation (8) due vertical in-situ tension and the tension over the pillar, Pp.

When applying Equation (8) to modeling a in-situ tensions values between 5 to 12 MPa and 20 to 100 MPa for the tension over the pillar, it is possible to observe that for a higher in-situ tension lower is the ore recovery index, and the higher the tension over the pillar, the higher will be the ore recovery (Figure 5).
2.2 Numerical modelling for previous initial situation
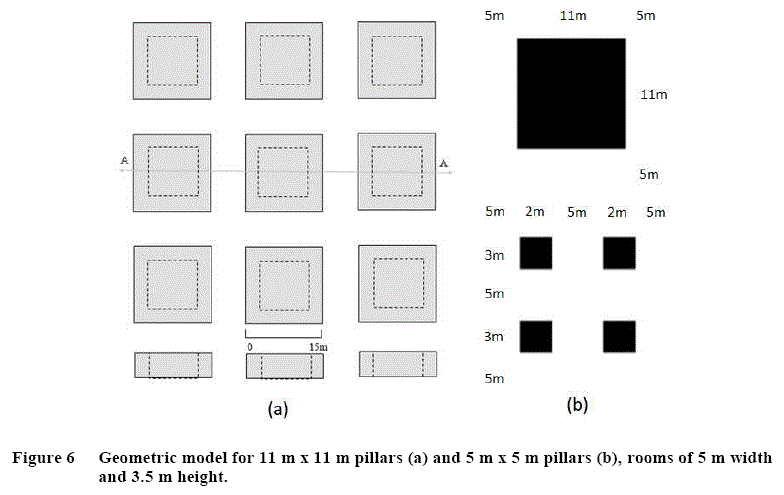
This research project aims to determine the optimum ore recovery for the manganese by applying the numerical model of FLAC3D. For the first phase, a model of MN-2 mining area was elaborated, this model represents the mining areas of Mariza Sul at a 150 m depth from the stope roof, pillars of para 11 m x 11 m and 5 m x 5 m, rooms of 5 m width and 3.5 m height (Figure 6). The Mohr-Coulomb and Hoeak-Brown breakage criteria were applied for this study.
The optimization of the 11 m x 11 m pillar area will be made with a lateral cut at the pillars, avoiding bringing harm to the pillar stability, as also creating a cross-section chamber in the center of the pillar and achieving a SF above 1.5 for both cases.
The FLAC3D routine uses FISH functions and variables that may be able to generate an automatic model for a predetermined number of pillars, with desired room and pillar dimensions. For this case, the rooms are orthogonal and together with the pillars have the same dimensions for each mine location.
The routine description depends on the function sequence and the main routine calls. The main routine (main.dat) execute automatically the full routine.
Sub-routine "functions.dat"
On this file, it can be found functions that are applied in the whole model as the time counting, geometric functions, input and output data.
Sub-routine "set_model.dat"
This file contains the variables declaration that are relevant to the evaluated model and includes rock; geometry; set-rocks; boundary; run in situ; run current state; pillar test.
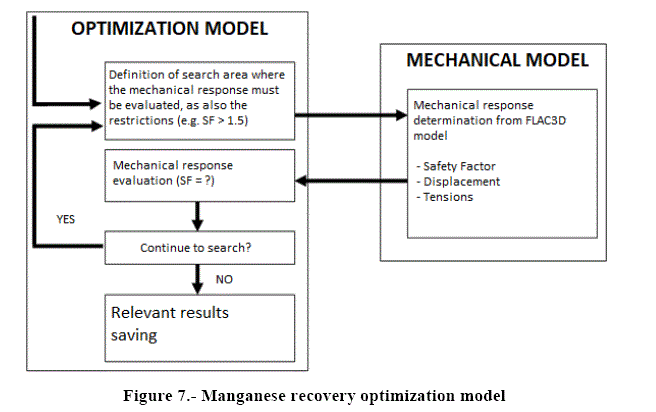
For this project there is a goal of developing a optimization model, where it have a optimization routine based on a numpy library from Python or other app that can perform the same task (Figure 7).
2.3 3D numerical model developing
The computational numerical model was developed for Urucum mine taking into consideration 68 lithological seams, alternating four mainly types corresponding to 270 m depth.
Forthe Mariza Sul mining areathere were implemented two numerical models at FLAC3D, considering 44 lithology with a 150 m height above the mining area and a homogeny rock with a 50 m depth under the mining level (Figure 8). The constitutive considered model was the Mohr-Coulomb and an instantaneous mining process was. On the other hand, the models comprehend of one pillar and other of nine pillars (3 x 3).
3 Results and discussion
Knowing the depth conditions of manganese MN-2 mining level, lithology above the level, rock blasting quality (D=0.8) and intact rock strength, the needed parameters for the numerical model can be estimated by the formula presented by Hoek et al. (Hoek, Carranza-Torres e Corkum, 2002).
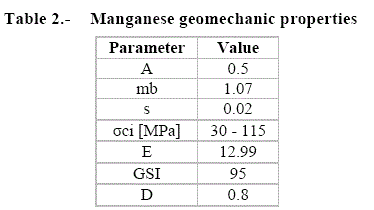
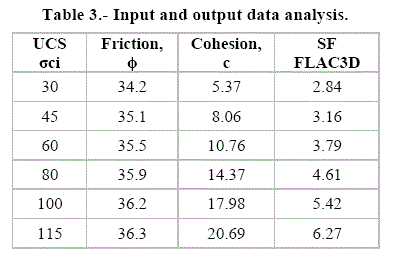
For the ore at MN-2, the following parameters were considered (Table 2) . By the following values, it was expected to see a variation at the input data due to the varying intact rock strength values. Because of that, this part of the Project was based by the intact rock strength variation.
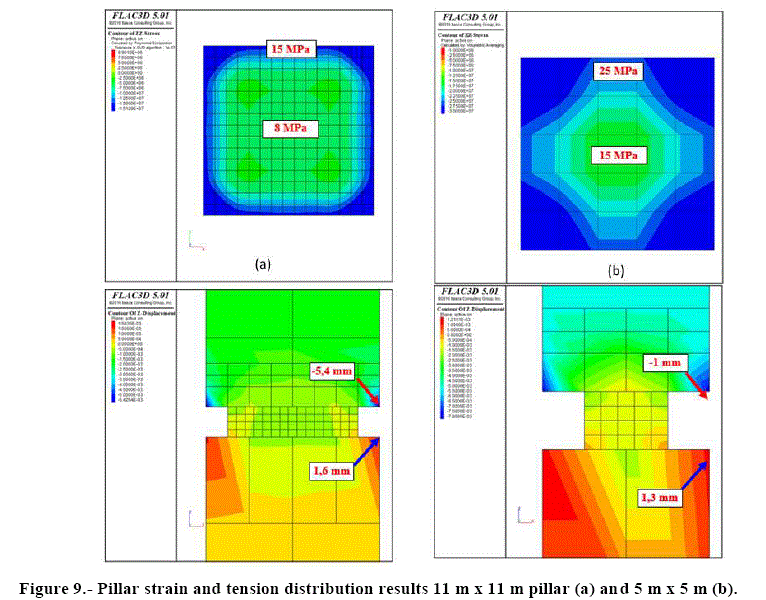
Figure 9 shows the maximum tension and strain limits for the rock, where is possible to observe a great tension increase for the 5 m x 5 m pillars when comparing with 11 m x 11 m pillars and vice-versa for the maximum strain.
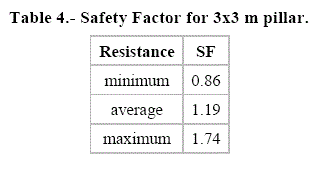
By intending to represent the pillar behavior in diverse conditions, it was selectthree strength levels: minimum of 30 MPa, average of 60 MPa and a maximum of 115 MPa (Table 4). For 11 m x 11 m pillar, the vertical tension results vary from 5 to 15 MPa with a displacement of 0.5 to 5 mm (Appendix A).
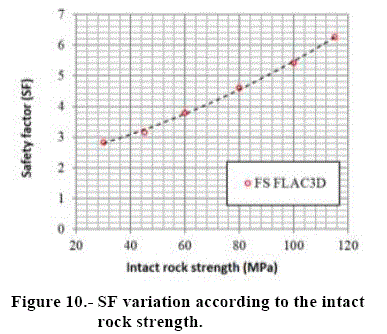
The input data (Table 2) applied fo FLAC3D analysis, determined a safety factor according to the intact rock strength. As can be seen at Table 3 and Figure 10, the obtained safety factor vary from 2.8 to 6.3.
As considering an initial possibility of mining perpendicular rooms of 5 m width (Figure 6.b) for the modeling, the model results can be seen at Figure 9.b. The safety factor was also evaluated for the three level strength, Table 4 shows the obtained SF values by the strength reduction method.
The used SF method (strength reduction method) by the software is compatible with the empirical formulas (Navarro Torres VF et al, 2011).
The variability of the obtained SF for Urucum mine case, when applied a rock strength of 30 to 115 MPa, a w/h = 3.1 and a depth of 150 m, resulted in SF values from 2.84 to 6.27. By this case, it could be well seen the sensibility of SF due to the room and pillar dimensions for both methodologies.
4 Conclusions
The developed 3D model shows an excellent flexibility, geometry and geomechanic adaptability that can be apply for many diverse scenarios, as the operational conditions varies during the mine phase of Urucum mine.
The presented routine was able to incorporate important conditions of the mine rock mass, as the lithology and the rock behavior, been possible to apply for one pillar to an unlimited number of pillars, with the possibility of simulating massive underground mining areas for many scenario cases.
The application of a computational 3D numerical model for 1 to 9 pillars, representing Mariza Sul mining area on a pessimist scenario (low to high compressible ore strength) showed a good compatibility, of a good scenario calibration for the conditions of the ore strength, been an important study tool for similar cases.
Acknowledgement
The author would like to acknowledge to Instituto Tecnologico VALE for sponsoring the present research work and SimWork for you participation as a Service Company.
References
Brandani, DB. (2011) Estudo do comportamento geomecânico de pilares esbeltos modelados em rocha dura na bacia do Corpo I, Mina Nova - Crixás/GO. Dissertação de mestrado professional, UFOP, 187p. [ Links ]
Hedley, DGF & Grant, F. (1972) Stope-and-Pillar Design for the Elliot Lake Uranium Mines. CIM Transaction, 7, pp. 121-128. [ Links ]
Hoek, E., Carranza Torres, E. & Corcum, B. (2002) Hoek-Brown Failure Criterium - 2002 Edition. NARMS, Toronto. [ Links ]
Kuhnhein, G & Ramer, R. (2004). The influence of horizontal stress on pillar design and mine layout at two underground limestone mines, [in] Proceeding of the 23rd International Conference on Ground Control in Mining, Morgantown, p.311. [ Links ]
Navarro Torres, VF & Vinueza, G. (2015) Análise e otimização da recuperação de minério de manganês na lavra por câmaras e pilares - Estudo de caso na mina de Urucum, 1a parte. Research Report of Instituto Tecnológico Vale, Ouro Preto Brazil, 24p. [ Links ]
Navarro Torres, VF, Da Gama C, Silva MC, Falcão P & Xie Q. (2011) Comparative stability analyses of traditional and selective room-and-pillar mining techniques for sub-horizontal tungsten veins. International Journal of Minerals, Metallurgy and Materials Volume 18, Number 1, February 2011, pp 1-8. [ Links ]
Stacey, TR & Page, CH. (1986) Practical Handbook for Underground Rock Mechanics, Series on Rock and Soil Mechanics, Trans Tech Publications, 12, pp. 53-63. [ Links ]
Verma, AK. (2014) A Comparative Study of Various Empirical Methods to Estimate the Factor of Safety of Coal Pillars. American Journal of Mining and Metallurgy, Vol. 2, No. 1, pag. 17-22. [ Links ]
Zipf, RK. (2001) Pillar design to prevent collapse of room and pillar mines. In Underground Mining Methods: Engineering Fundamentals and International Case Studies. Edited by W.A. Hustrulid and R.L. Bullock. Littleton, CO: SME. pp. 493-496. [ Links ]