Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Investigación & Desarrollo
versión impresa ISSN 1814-6333versión On-line ISSN 2518-4431
Inv. y Des. vol.21 no.1 Cochabamba 2021
DOI: 10.23881/idupbo.021.1-6i
ARTÍCULOS - INGENIERÍAS
ESTUDIO COMPARATIVO SOBRE MODELOS DE TURBULENCIA EN FLUJO DE REFRIGERANTES CON BAJO GWP EN EL INTERIOR DE MICROCANALES
RANS TURBULENCE MODELS PERFORMANCE TO PREDICT HEAT TRANSFER CHARACTERISTICS OF LOW GWP FLUIDS FLOW IN MICROCHANNELS
Eduardo Miranda1, Daniel Sempértegui-Tapia2 y Cristian Chávez1
1Departamento de Ingeniería Mecánica
Universidad de La Serena, La Serena, Chile
2Centro de Investigaciones Opticas y Energia (CIOE)
Universidad Privada Boliviana
(Recibido el 12 de junio 2021, aceptado para publicación el 16 de julio 2021)
RESUMEN
Este artículo se trata de una evaluación de modelos de turbulencia para la predicción de la pérdida de presión y el coeficiente de transferencia de calor durante el flujo de refrigerantes con bajo GWP en el interior de microcanales. En este estudio, características de mecánica de fluidos y transferencia de calor se simulan incorporando condiciones de flujo turbulento en un microcanal circular de 1.1 mm de diámetro. Los modelos de turbulencia con las formulaciones k - ε y k - ω son evaluados para números de Reynolds hasta 10000 y son implementados computacionalmente en el software OpenFoam. Los perfiles de velocidad, factores de fricción y números de Nusselt son calculados y analizados en función de variables paramétricas. Los resultados numéricos son validados con métodos de predicción analíticos y con datos experimentales medidos en trabajos previos para flujos de R134a, R1234fy, R1234ze(E) y R600a. La variación de la caída de presión y coeficiente de transferencia de calor convectivo son analizados de acuerdo al efecto al tipo de fluido y al modelo de turbulencia empleado. Los resultados indican que los modelos describen cualitativamente el comportamiento del flujo y la transferencia de calor en condiciones de turbulencia. Cuantitativamente, los modelos Low-Re k - ε, k - ω estándar y k - ω SST presentan mejores predicciones para las variables de interés. Por otro lado, el modelo Low-Re k - ε presenta el menor error medio absoluto.
Palabras Clave: Turbulencia, Microcanales, Numérico, Caída de Presión, Transferencia de Calor.
ABSTRACT
This paper evaluates the capacity of the following turbulence models: standard k - ε, RNG k - ε, k - ω standard, k - ω SST, Realizable k - ε and Low-Re k - ε to predict the fluid mechanics and heat transfer characteristics of low GWP fluid flow in a 1.1 mm ID microchannel. These turbulence models were evaluated for Reynolds Numbers up to 104. The numerical results for velocity profile, friction factors and Nusselt Numbers are validated with analytical and experimental data published in previous works for R134a, R1234yf, R1234ze(E) and R600a. Parametric behaviors of pressure drop and heat transfer coefficient are presented and analyzed. The results indicate that each of the models describes the qualitative behavior of flow and heat transfer processes. On the other hand, the quantitative results indicate that the Low-Re k - ε, k - ω and k - ω SST models demonstrate an acceptable prediction of some variable’s behavior. Numerically, the Low-Re k - ε model presents an accurate prediction with the lowest mean absolute.
Keywords: Turbulence, Microchannels, Numerical, Pressure Drop, Heat Transfer.
1. INTRODUCCIÓN
El desarrollo de dispositivos electrónicos se ha incrementado considerablemente durante la última década, enfocándose en el diseño de componentes a micro-escala. La implementación de microcanales para la remoción de calor es considerada una de las soluciones de mayor factibilidad técnica en dispositivos de alta densidad energética, sin embargo, se deben buscar estrategias para mejorar el desempeño térmico del dispositivo. Una opción para mejorar la transferencia de calor en microcanales es emplear flujos en régimen turbulento. La turbulencia ha demostrado mejorar el coeficiente de transferencia de calor, aumentando la remoción de calor y posibilitando la disminución del área de flujo [1], aminorando considerablemente los costos de fabricación. Sin embargo, el estudio de la turbulencia implica la inclusión de incertezas inherentes a la modelación física y matemática. En el modelaje de la turbulencia, los modelos Reynolds Averaged Navier Stokes (RANS) gozan de cierta popularidad debido a las ventajas de implementación y a las bajas exigencias computacionales que exigen. No obstante, los estudios reportados en la literatura sugieren que los modelos de turbulencia RANS varían su precisión respecto a las condiciones de flujo en microcanales. Diversos autores han reportado estudios de turbulencia en microcanales [2], [3], [4], [5] y [6] para la predicción de las variables de interés en el diseño: factor de fricción, caída de presión, coeficiente de transferencia de calor, fracción de vacío, etc. Sin embargo, los resultados reportados son concluyentes respecto a que, cualitativa y cuantitativamente, los modelos RANS no son precisos y no están claras las condiciones en las que entregan resultados coherentes con lo experimental en flujos monofásicos y bifásicos.
En este sentido, el presente estudio profundiza el análisis de modelos de turbulencia populares, con el fin de determinar los niveles de incerteza que cada uno entrega en simulaciones de flujos turbulentos en microcanales. El estudio se realiza en base al trabajo experimental realizado por Sempertegui-Tapia y Ribatski [7], enfocando el análisis en el flujo monofásico turbulento reportado por los autores. Los modelos de turbulencia estudiados son el modelo k - ε, RNG k - ε, k – ω standard y k – ω SST. El análisis comparativo se realiza en relación a magnitudes físicas relevantes al diseño de microcanales: el factor de fricción, la caída de presión lineal, el esfuerzo de corte en la pared, el coeficiente de transferencia de calor y el número de Nusselt. Las diferencias en la modelación, las diferencias en la predicción de la transferencia de calor para cada refrigerante y la precisión de cada modelo de turbulencia respecto a los resultados reportados por Sempertegui-Tapia y Ribatski [7], son discutidas a lo largo del presente trabajo.
2. MARCO TEORICO
A continuación, son descritos brevemente los modelos de turbulencia RANS que serán simulados en el presente artículo.
2.1 Modelos del grupo k - ε
Este modelo de turbulencia cierra el sistema agregando las ecuaciones del transporte de energía cinética turbulenta y la disipación de energía cinética turbulenta. Ambas magnitudes físicas se relacionan por medio de la viscosidad turbulenta, la que es definida como:
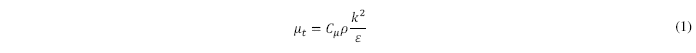
El transporte de las magnitudes físicas relacionadas a la turbulencia viene dado por las siguientes ecuaciones:
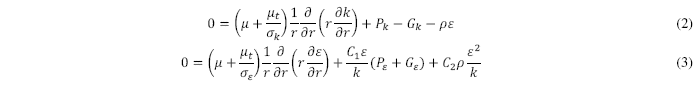
donde Pk y Gk representan la producción/destrucción de energía cinética turbulenta, respectivamente. De forma análoga, los términos Pε y Gε representan la producción/destrucción de disipación de energía cinética turbulenta en el dominio. El modelo k - ε aborda la zona cercana a la pared empleando funciones de pared o bien resolviendo la sub-capa laminar a través de formulaciones especiales para bajos números de Reynolds. El presente trabajo estudia las dos opciones, empleando las funciones de pared standard y la formulación de bajo número de Reynolds propuesta por Lien y Leschziner [8]. Las constantes de cierre del modelo varían según la formulación y pueden ser consultadas en el trabajo de Launder y Spalding [9]. El estudio incluye a los modelos RNG k - ε ([10]) y k - ε realizable ([11]).
2.2 Modelos del grupo k - ω
Este modelo emplea la energía cinética turbulenta y la disipación de energía cinética turbulenta específica (ω) como variables de cierre. La disipación de energía cinética turbulenta es sustituida por ![]() en las ecuaciones (2) y (3), resultando en el siguiente conjunto de ecuaciones:
en las ecuaciones (2) y (3), resultando en el siguiente conjunto de ecuaciones:
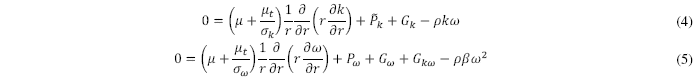
donde ![]() y
y ![]() representan la producción/destrucción de energía cinética turbulenta (análogo para
representan la producción/destrucción de energía cinética turbulenta (análogo para ![]() ). El término
). El término ![]() representa la difusión cruzada en el flujo turbulento ([12]), la que estabiliza la modelación logrando independizar los cálculos respecto a los valores flujo libre (totalmente turbulento). La viscosidad turbulenta es definida mediante la expresión:
representa la difusión cruzada en el flujo turbulento ([12]), la que estabiliza la modelación logrando independizar los cálculos respecto a los valores flujo libre (totalmente turbulento). La viscosidad turbulenta es definida mediante la expresión:
![]()
Los coeficientes usados en el cierre del sistema de ecuaciones son: Cμ = 0.09, α = 0.52, β = 0.072 y αk = αω = 0.5. El estudio incluye el modelo k - ω SST, el cual puede ser consultado en [13].
Las condiciones de borde en la entrada del flujo, asociadas a todos los modelos de turbulencia, son las siguientes:
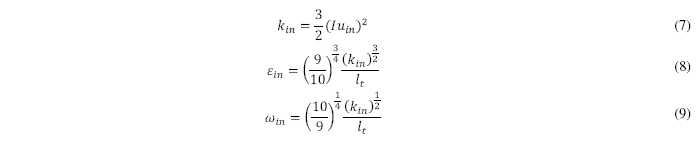
donde lt es la longitud característica de la turbulencia y I es la intensidad de la turbulencia en el microcanal. Dichos valores se definen como lt = 0.07Dflow I = 0.16Re-1/8. En la pared, los valores de las variables son k = 0 (m2/s2), ω = (4000μ/ρRa)(1/s) y ε = ∞(m2/s2) ([14]; [15]), donde Ra es la rugosidad del microcanal. El contorno de salida es modelado aplicando condición de flujo desarrollado en todas las variables.
3. MODELO FÍSICO
La situación física es estudiada con el esquema mostrado en la Figura 1. El dominio es separado en dos zonas: zona de desarrollo hidrodinámico y zona de calentamiento. La zona de calentamiento (diabática) es equivalente a la zona de pre-calentamiento detallada en estudios previos ([16], [17]). La colocación de una zona de desarrollo hidrodinámico asegura que el perfil de velocidades a la entrada de la zona de calentamiento sea completamente desarrollado. Las dimensiones del microcanal son Lh = 0.2 m, Ld= 5Lh y Dflow = 0.0011 m.
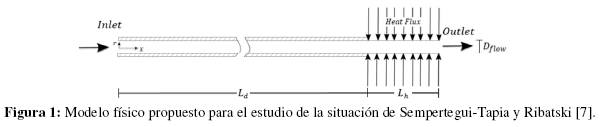
Los refrigerantes estudiados son: R134a, R1234ze(E), R1234yf, R600a. Las características de mecánica de fluidos y transferencia de calor son evaluadas en cada fluido variando el número de Reynolds. Con el objetivo de ver la diferencia entre los fluidos, la Tabla 1 muestra las propiedades termofísicas más relevantes de líquido saturado a una temperatura de saturación de 31°C de los 4 fluidos estudiados.

El modelo matemático se basa en balances locales de cantidad de movimiento y energía. El estudio es realizado partiendo de las siguientes hipótesis: el flujo es permanente e incompresible, es totalmente desarrollado y las propiedades del fluido se mantienen constantes dentro del rango de temperaturas trabajadas. El estudio contempla flujo monofásico turbulento de refrigerante a través del microcanal. La turbulencia es modelada con modelos RANS, utilizando los modelos standard κ - ε, RNG κ - ε, κ – ω standard y κ – ω SST. El sistema de ecuaciones diferenciales parciales queda reducido al análisis del transporte de momentum en la dirección x y al transporte de calor por convección y conducción dentro de microcanal. Empleando la suposición de Boussinesq para los esfuerzos de Reynolds, es posible expresar las ecuaciones de momentum y energía como se muestra a continuación:
![]()
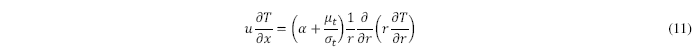
Las condiciones de contorno son: no deslizamiento en las paredes, velocidad uin y temperatura Tin uniformes a la entrada del microcanal. Las paredes de la zona de desarrollo hidrodinámico (0<x<Ld ) son adiabáticas, mientras que en la zona de calentamiento se aplica flujo de calor constante ![]() . La situación física es abordada asumiendo simetría axial en el eje longitudinal, calculando numéricamente la parte media-superior del dominio computacional. El contorno de salida es modelado aplicando condición de flujo desarrollado en todas las variables dependientes
. La situación física es abordada asumiendo simetría axial en el eje longitudinal, calculando numéricamente la parte media-superior del dominio computacional. El contorno de salida es modelado aplicando condición de flujo desarrollado en todas las variables dependientes ![]() .
.
4. VALIDACIÓN
El modelo físico y matemático ha sido implementado en OpenFOAM v19.12. La validación de la implementación computacional es realizada abordando el modelo base conformado por las ecuaciones (10) y (11). El régimen laminar es usado en la comparación de resultados para evitar el sesgo de los modelos de turbulencia y así validar el modelo base. El algoritmo SIMPLE (Versteeg y Malalasekera [18]) es utilizado para la solución del sistema de ecuaciones. Los parámetros considerados en la simulación numérica son Re = 250, malla 360 x 45 refinada en la dirección radial, criterio de convergencia de 10-6 en las variables dependientes, factor de relajación de 0.5 en velocidad y temperatura. La Figura 2 presenta la comparación de los resultados numéricos con respecto a la solución analítica de la ecuación (10) en régimen laminar:
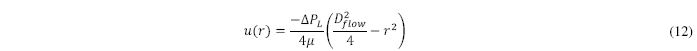
Las distribuciones de velocidad descrita analítica y numéricamente se superponen entre sí, sugiriendo que son idénticas. La desviación máxima de la solución numérica respecto a la analítica es de 0.54%.
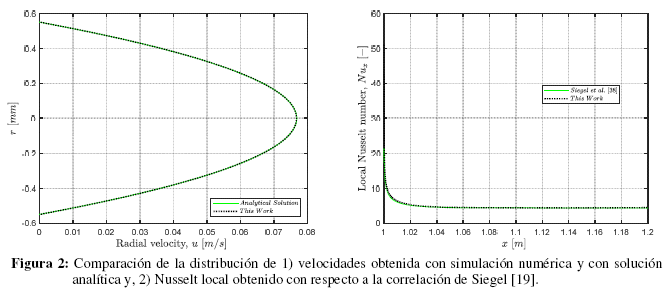
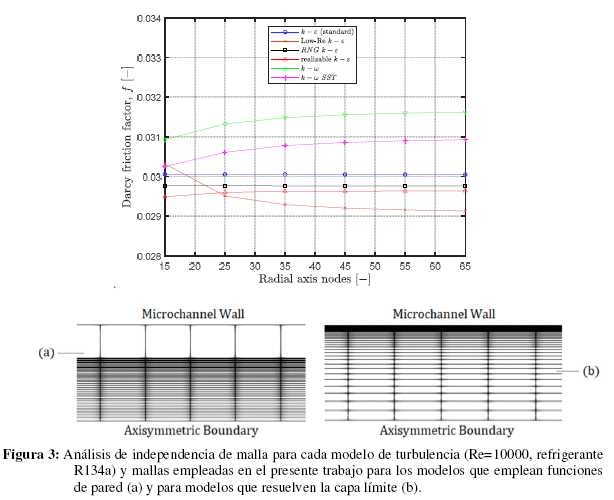
La transferencia de calor es comparada en la Figura 2b, donde la solución numérica para el número de Nusselt en la zona de calentamiento es comparada respecto a la correlación propuesta por Siegel [19]. Esta correlación indica que el número de Nusselt en un ducto de sección circular varía principalmente con respecto al número de Reynolds y la longitud del tramo donde un flujo de calor constante es aplicado. De acuerdo a la figura, la solución numérica presenta una secuencia considerablemente próxima a la correlación de Siegel, con una desviación media de 2.1%. Los resultados mostrados corroboran la validez del modelo base empleado en el presente estudio, permitiendo la incorporación de los efectos de turbulencia a través de los modelos RANS. El estudio inicia con el análisis de convergencia de malla. La cantidad de nodos en la dirección x es fijada en 60 nodos en la zona de desarrollo hidrodinámico y 500 nodos en la zona de calentamiento, valores que previamente se han demostrado como apropiados para la descripción de la situación física. El mallado en la dirección radial se evaluó usando 15, 25, 35, 45, 55 y 65 nodos, tomando la situación Re = 10000 como caso límite. El análisis es realizado considerando un primer nodo grueso para los modelos que emplean funciones de pared (con y+>30 para el caso límite), mientras que en el resto de modelos se emplea una malla refinada hacia la pared del microcanal con el fin de resolver apropiadamente los gradientes de la capa límite. La Fig. 4 muestra la variación del factor de fricción en función del mallado en la dirección radial, sugiriendo que 35 nodos es una cantidad razonable para asegurar convergencia de malla. El error máximo del factor de fricción empleando la malla de 35 nodos es del 0.38% respecto de la malla evaluada más fina. Las mallas utilizadas en el estudio son mostradas en la Fig. 3. Los modelos k - ε (standard), RNG k - ε y realizable k - ε emplean la malla con un nodo grueso en la pared para un uso apropiado de las funciones de pared, mientras que los modelos k - ε de bajo número de Reynolds, k - ω y k - ω SST emplean la malla refinada hacia la pared para resolver los gradientes en la capa límite.
5. RESULTADOS Y DISCUSIÓN
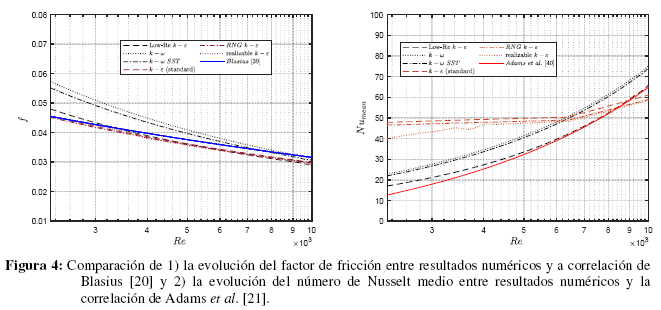
La Figura 4 compara los resultados numéricos del factor de fricción con respecto a la correlación de Blasius [20], ampliamente utilizada en el estudio de flujos turbulentos. El refrigerante R134a es usado en esta comparación. Los resultados numéricos se ajustan considerablemente bien a la correlación. Los modelos que emplean funciones de pared son los que tienen mejor ajuste, indicando que la adición de un nodo grueso es una estrategia que entrega mejores resultados cuando se predicen los gradientes de velocidad, reportando un error medio aproximado del 5%. Los modelos k - ε de bajo número de Reynolds, k - ω y k - ω SST, tienen una mayor desviación la que se acentúa en Reynolds cercanos a 2300 que varía desde un 20 a 0.06% en estos últimos. La Figura 7 muestra la comparación del Nusselt numérico respecto a la correlación propuesta por Adams et al. [21], para el refrigerante R134a. El buen ajuste del modelo k - ε de bajo número de Reynolds es evidente, siendo la que mejor se acerca a la correlación de Adams et al. Por otra parte, los modelos de la familia k - ω reportan la misma evolución del número de Nusselt respecto al aumento del número de Reynolds, aun cuando existe un evidente sobredimensionamiento aproximado del 20% respecto a la correlación. Al contrario, los modelos con funciones de pared no describen apropiadamente la transferencia de calor para Reynolds, reportando resultados no físicos en el rango de número de Reynolds evaluados. La evolución del número de Nusselt descrita por estos modelos se explica por la incapacidad que tienen las funciones de pared (térmicas) en la descripción en la sub-capa laminar y la capa amortiguadora. Empleando las funciones de pared térmicas standard, el valor crítico de y* donde la solución lineal y la solución logarítmica se intersectan es y*=8 para el refrigerante R134a. El valor crítico de y* es alcanzado por los modelos k - ε (standard), RNG k - ε y realizable k - ε alrededor de Re=6365 y en consecuencia, por debajo de este valor los modelos emplean la función lineal T*=y*Pr, describiendo inapropiadamente la transferencia de calor e implicando un sobredimensionamiento del número de Nusselt. La predicción mejora a medida que aumenta el número de Reynolds por sobre Re=6365, no obstante en Re=10000 solo se alcanza un valor de y* cercano a 11 en los modelos evaluados con funciones de pared, siendo una cantidad insuficiente ya que por sobre y*>30 las funciones de pared entregan resultados razonablemente precisos según la literatura. El aumento de y* implica el aumento del tamaño del nodo grueso en la pared, lo que mermaría la predicción de la distribución de velocidades y temperatura en la sección transversal del canal. Esto sugiere que emplear funciones de pared en el rango de velocidades evaluado no es viable en la práctica, especialmente para la predicción térmica. Debido a esta discusión, el trabajo se limita al estudio de los modelos k - ε de bajo número de Reynolds, k - ω y k - ω SST.
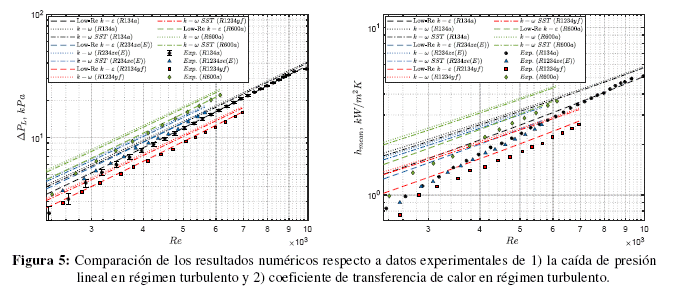
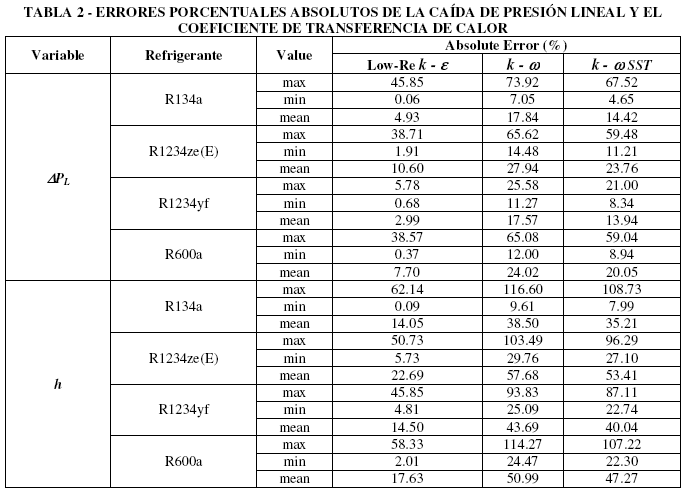
La Fig. 5 muestra la comparación de los resultados numéricos respecto a los datos experimentales del coeficiente de transferencia de calor respecto a los datos de Sempértegui y Ribatski [7]. En este caso, los modelos de turbulencia no describen de forma precisa los datos experimentales en la mayoría de los diferentes Reynolds evaluados. En general, el modelo k - ε de bajo número de Reynolds es el que mejor se aproxima a los valores experimentales, sin embargo los errores medios rondan el 17%. Las predicciones de los modelos para el coeficiente de transferencia de calor en números de Reynolds cercanos a 2300 sobredimensionan completamente los resultados experimentales. No obstante, modelo k - ε de bajo número de Reynolds mejora la descripción al acercarse a Re = 6000, logrando un buen ajuste respecto a los datos experimentales con un error aproximado del 3% en el último tramo. De igual forma, los modelos k - ω y k - ω SST mejoran su predicción en dicho tramo logrando errores mínimos de 9.61 y 7.99%, respectivamente. Los errores obtenidos por debajo de Re = 6000 aumentan considerablemente, sobredimensionando la caída de presión lineal y el coeficiente de calor. Los errores máximos, mínimos y medios de la caída de presión lineal y del coeficiente de transferencia de calor, son listados en la Tabla 2.
Los modelos de turbulencia sobredimensionan considerablemente los valores al comienzo del rango evaluado. Sin embargo, existe una notoria diferencia entre las características de mecánica de fluidos y de transferencia de calor en el número de Reynolds en el que los valores comienzan a tender a los datos experimentales. Esto se explica con la diferencia de las velocidades de difusión inherentes a las propiedades de los refrigerantes evaluados. La mejor precisión es obtenida con el modelo k - ε de bajo número de Reynolds. Existen diversas formulaciones del modelo k - ε para lograr mayor estabilidad en los cálculos en bajo número de Reynolds. Sin embargo, no todas siguen la misma metodología ni formulación (ni constantes de cierre) por lo que los resultados podrían varían sustancialmente. El presente trabajo demuestra que la metodología propuesta por Lien y Leshziner entrega una precisión razonablemente buena en la modelación de turbulencia en microcanales.
6. CONCLUSIONES
El presente trabajo estudia la modelación numérica de la turbulencia en microcanales con refrigerantes de bajo GWP, empleando los modelos de turbulencia k - ε standard y de bajo número de Reynolds, RNG k - ε, realizable k - ε, k - ω y k - ω SST . La resolución de la sub-capa laminar entrega mejores resultados en la predicción de los gradientes de térmicos, comparado con el uso de funciones de pared en la modelación de la turbulencia en microcanales. Sin embargo, la predicción obtenida con esta metodología es fuertemente dependiente del modelo de turbulencia empleado. La velocidad media no es suficientemente alta para desarrollar la turbulencia por sobre el nivel y*>30, implicando dificultades en la descripción de los gradientes térmicos por parte de los modelos con funciones de pared. No obstante, las variables asociadas al gradiente de velocidad se logran predecir aceptablemente. Por otro lado, los modelos son incapaces de predecir con exactitud las características del flujo en Reynolds cercanos a 2300, debido a la fuerte presencia de fuerzas viscosas. La descripción física mejora con el aumento del número de Reynolds. Los modelos k - ε de bajo Reynolds, k - ω y k - ω SST escriben satisfactoriamente las variables asociadas a la mecánica de fluidos. Sin embargo, los modelos k - ω y k - ω SST sobredimensionan el coeficiente de transferencia de calor aproximadamente en un 25%, dentro del rango de Re considerado en el presente trabajo. El modelo k - ε de bajo Reynolds de Lien y Leshziner reporta desviaciones entre 0.1 a 15% dependiendo del número de Reynolds, convirtiéndose en una opción viable para la descripción de la turbulencia en microcanales.
REFERENCIAS
[1] Y. Zhai, G. Xia, Z. Chen, and Z. Li, “Micro-PIV study of flow and the formation of vortex in micro heat sinks with cavities and ribs,” Int. J. Heat Mass Transf., vol. 98, pp. 380–389, 2016, doi: 10.1016/j.ijheatmasstransfer.2016.03.044.
[2] M. Ciofalo, J. Stasiek, and M. W. Collins, “Investigation corrugated of flow and heat transfer Numerical simulations,” Int. J. Heat Mass Transf., vol. 39, no. 1, pp. 165–192, 1996.
[3] D. Xu, T. Y. Ng, L. S. Pan, K. Y. Lam, and H. Li, “Numerical simulations of fully developed turbulent liquid flows in micro tubes,” J. Micromechanics Microengineering, vol. 11, no. 3, pp. 175–180, 2001, doi: 10.1088/0960-1317/11/3/303.
[4] P. Asinari, “Numerical prediction of turbulent convective heat transfer in mini/micro channels for carbon dioxide at supercritical pressure,” Int. J. Heat Mass Transf., vol. 48, no. 18, pp. 3864–3879, 2005, doi: 10.1016/j.ijheatmasstransfer.2005.03.028.
[5] M. K. Sung and I. Mudawar, “Experimental and numerical investigation of single-phase heat transfer using a hybrid jet-impingement/micro-channel cooling scheme,” Int. J. Heat Mass Transf., vol. 49, no. 3–4, pp. 682–694, 2006, doi: 10.1016/j.ijheatmasstransfer.2005.08.021.
[6] S. Blonski, P. M. Korczyk, and T. A. Kowalewski, “Analysis of turbulence in a micro-channel emulsifier,” Int. J. Therm. Sci., vol. 46, no. 11, pp. 1126–1141, 2007, doi: 10.1016/j.ijthermalsci.2007.01.028.
[7] D. F. Sempértegui-Tapia and G. Ribatski, “Flow boiling heat transfer of R134a and low GWP refrigerants in a horizontal micro-scale channel,” Int. J. Heat Mass Transf., vol. 108, pp. 2417–2432, 2017, doi: 10.1016/j.ijheatmasstransfer.2017.01.036.
[8] F. S. Lien and M. A. Leschziner, “A pressure-velocity solution strategy for compressible flow and its application to shock/boundary-layer interaction using second-moment turbulence closure,” J. Fluids Eng. Trans. ASME, vol. 115, no. 4, pp. 717–725, 1993, doi: 10.1115/1.2910204.
[9] B. E. Launder and D. B. Spalding, “The numerical computation of turbulent flows,” Comput. Methods Appl. Mech. Eng., vol. 3, pp. 269–289, 1974, doi: 10.1007/JHEP10(2012)057.
[10] V. Yakhot, S. A. Orszag, S. Thangam, T. B. Gatski, and C. G. Speziale, “Development of turbulence models for shear flows by a double expansion technique,” Phys. Fluids A, vol. 4, no. 7, pp. 1510–1520, 1992, doi: 10.1063/1.858424.
[11] T. H. Shih, W. W. Liou, A. Shabbir, Z. Yang, and J. Zhu, “A new k-ε eddy viscosity model for high Reynolds number turbulent flows,” Comput. Fluids, vol. 24, no. 3, pp. 227–238, 1995, doi: 10.1007/978-3-319-27386-0_7.
[12] D. C. Wilcox, “Formulation of the k-ω turbulence model revisited,” AIAA J., vol. 46, no. 11, pp. 2823–2838, 2008, doi: 10.2514/1.36541.
[13] F. R. Menter, “Two-equation eddy-viscosity turbulence models for engineering applications,” AIAA J., vol. 32, no. 8, pp. 1598–1605, 1994, doi: 10.2514/3.12149.
[14] F. R. Menter and T. Esch, “Elements of industrial heat transfer predictions,” 16th Brazilian Congr. Mech. Eng., 2001.
[15] R. A. W. M. Henkes, F. F. Van Der Vlugt, and C. J. Hoogendoorn, “Natural-convection flow in a square cavity calculated with low-Reynolds-number turbulence models,” Int. J. Heat Mass Transf., vol. 34, no. 2, pp. 377–388, 1991, doi: 10.1016/0017-9310(91)90258-G.
[16] D. F. Sempértegui-Tapia and G. Ribatski, “Two-phase frictional pressure drop in horizontal micro-scale channels : Experimental data analysis and prediction method development,” Int. J. Refrig., vol. 79, pp. 143–163, 2017, doi: 10.1016/j.ijrefrig.2017.03.024.
[17] D. F. Sempértegui-Tapia, J. De Oliveira Alves, and G. Ribatski, “Two-Phase flow characteristics during convective boiling of halocarbon refrigerants inside horizontal small-diameter tubes,” Heat Transf. Eng., vol. 34, no. 13, pp. 1073–1087, Oct. 2013, doi: 10.1080/01457632.2013.763543.
[18] H. K. Versteeg and W. Malalasekera, An Introduction to Computational Fluid Dynamics: The finite VOlume Method, 2nd ed., vol. 2nd Editio. 2007.
[19] R. Siegel, E. M. Sparrow, and T. M. Hallman, “Steady laminar heat transfer in a circular tube with prescribed wall heat flux,” Appl. Sci. Res. Sect. A, vol. 7, no. 5, pp. 386–392, 1958, doi: 10.1007/BF03184999.
[20] H. Blasius, “Das ahnlichkeitsgesetz bei reibungsvorg/ingen in fltissigkeiten,” Forschg. Arb. Ing. Wes., vol. 131, 1913.
[21] T. M. Adams, S. I. Abdel-Khalik, S. M. Jeter, and Z. H. Qureshi, “An experimental investigation of single-phase forced convection in microchannels,” Int. J. Heat Mass Transf., vol. 41, no. 6–7, pp. 851–857, 1998, doi: 10.1016/S0017-9310(97)00180-4.














