DOI: 10.23881/idupbo.020.1-8i

ARTÍCULOS - INGENIERÍAS

 

SLOPE STABILITY ANALYSIS BY FINITE ELEMENTS: A CASE STUDY IN LA PAZ-BOLIVIA

 

ANÁLISIS DE ESTABILIDAD DE TALUDES MEDIANTE EL EMPLEO DE ELEMENTOS FINITOS: UN CASO DE ESTUDIO EN LA PAZ – BOLIVIA

 

 

Daniela Gurruchaga R., Fabiana Viscarra A.

Facultad de Ingenierías y Arquitectura
Universidad Privada Boliviana

fabianaviscarra@upb.edu

(Recibido el 29 de mayo 2020, aceptado para publicación el 25 de junio 2020)

 

 

---

ABSTRACT 

The geomechanically analysis of slopes is one important application within the geotechnical engineering scope; this fact comprehends the evaluation of natural or artificial slope stability conditions. Such evaluation process can be optimized by means of modelling combined with engineer criteria. It is important to apply a mathematical model that focuses in the analysis objective and expected results; stress-strain methods allow determining the resistant and deformational parameters in a slope, being capable to reproduce its natural behavior [1]. The present research applies to a specific sector of La Paz city, named Villa Exaltación. The objective of this study is the performing of slope stability analysis through finite elements, in order to determine the areas that need remediation.  The evaluation of stability alternatives it is also included. These alternatives go from simple remediation techniques (unstable material removal, slope undercut, inclination reduction, toe counterweight) to complex stabilization works such as pile curtains. The results reveal that a head slope undercut technique can bring stable conditions and minimal strain generation, being a satisfactory and feasible answer with low complexity works. Finally, verification was performed by means of limit equilibrium analysis. Both methodologies show satisfactory results, demonstrating that numerical methods are more representative and conservative. The calibration process of soil parameters plays a key role for the generation of a reliable model; critical conditions were simulated in order to determine minimal parameters needed for a stable slope. 

Keywords: Slope stability analysis, slope, finite elements, Factor of Safety, Limit Equilibrium.

---

 RESUMEN

Una aplicación importante de la ingeniería geotécnica es el análisis geomecánico de taludes que comprende el análisis de las condiciones de estabilidad de una ladera o talud artificial; este proceso puede ser optimizado a través de modelaciones, combinadas con el criterio del ingeniero. Dentro de las diferentes metodologías de modelación matemática, es importante emplear aquella que se enfoque en el objetivo del análisis y los resultados esperados, las modelaciones mediante métodos tensión-deformación permiten determinar los parámetros resistentes y deformacionales de una ladera, pudiendo reproducir el comportamiento real observado [1]. La presente investigación aplica a un sector específico de la ciudad de La Paz, denominado Villa Exaltación. El objetivo de este estudio radica en realizar un análisis de estabilidad de taludes mediante el método de elementos finitos para determinar las zonas donde sea necesaria la remediación. En este sentido, el estudio se complementa con análisis de alternativas de estabilización que permitan mejorar la estabilidad en curso de la zona de estudio. Dichas alternativas abarcan desde técnicas simples (remoción total de materiales inestables, corte de cabeza de talud, abatimiento de pendiente, contrapeso) hasta obras complejas de estabilización (cortina de pilotes). Los resultados revelan que, mediante un corte de cabeza de talud, se obtiene un factor de seguridad estable y deformaciones mínimas, demostrando de esta manera que es factible la implementación de obras civiles de baja complejidad, para obtener resultados satisfactorios. Finalmente se realizan verificaciones con métodos de cálculo simples basados en equilibrio límite. Los resultados, satisfactorios por ambas metodologías de cálculo, demuestran que los métodos numéricos son más representativos y además conservadores. Es importante considerar que el proceso de calibración de los parámetros del suelo, en un proceso significativo para generar una modelación numérica fiable; en el presente caso se simularon condiciones críticas para determinar los parámetros mínimos que brindarían sostenimiento al talud.

Palabras Clave: Análisis de Estabilidad, Taludes, Elementos Finitos, Factor de Seguridad, Equilibrio Límite.

---

 

 

1. INTRODUCTION

La Paz is considered as one of the most vulnerable cities in Bolivia, in terms of landslides. Due to its particular topography, unstable geological conditions and frequent human intervention, people´s safety and economy are compromised [2]. Villa Exaltación is a sector of La Paz located in the border region between the southeast area of El Alto city and the upper region of the Alpacoma’s river basin. According to the Risk Map (2011), Villa Exaltación presents a high-risk index, as a result of a moderate vulnerability level and a high hazard range, due to its natural characteristics and surroundings with the population [3].This sector is catalogued as high priority zone for intervention. This paper therefore intends to analyze how critical the stability is and how it can be improved through the modelling of stability alternatives for hazard mitigation.

In order to acquire the most suitable solution, it is important to understand the mechanisms that have generated or may generate potential slope failure. For such purpose, landslide inventory and technical data collection with a chronological sequence are valuable sources. Once slope failure mechanisms are understood, a method of analysis that best fits the situation can be selected. Alternatives evaluation can provide exact numerical values that may arise the solution feasibility. However, it is important to remember that soil materials are highlighted by their degree of complexity, which makes behavior prediction very difficult since these materials are heterogeneous in space and depth. The use of a remediation technique should be accompanied by an instrumentation or monitoring system that shall reduce uncertainty and, finally, validate the adopted solution. Since these kinds of systems are time and cost consuming, they are not often used.

 

2. ANALYSIS METHODS FOR SLOPE STABILITY 

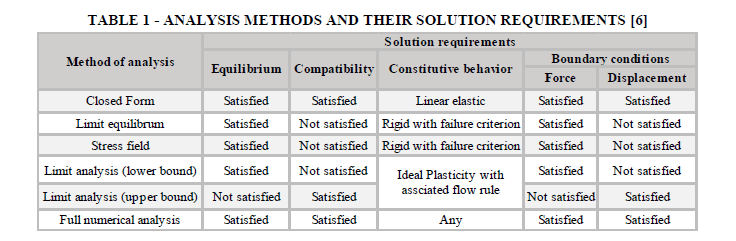
There are different methods of analysis that can be used by geotechnical engineers to determine slope stability conditions. These methods can be divided into three general groups: theoretical (Closed form), simple and numerical analysis [4]. The difference between them relies in the general solution’s requirements that each one meets. It is fundamental to acknowledge which of the four requirements are satisfied before considering a specific method. These requirements are: equilibrium, compatibility, constitutive behavior and boundary conditions [5].

■ Equilibrium has two components: global and internal equilibrium. In the first one, forces and moments are associated throughout the solution of their equations.  In the second one, stresses must be stablished in order to satisfy certain partial differential equations, which are:

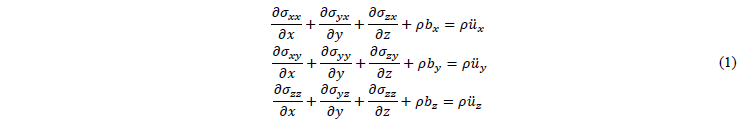
where , , , , , and  are the Cartesian components of total stresses.

Former equation can be expressed as follows:

where  is the transpose of the differential operator defined as:

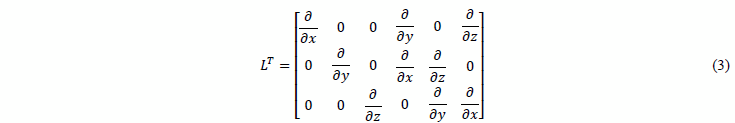
Therefore, equilibrium is related to stresses σ, mass forces ρb and the inertial forces assembled in vector ρ. In addition, density and the displacement vector are expressed as ρ and U respectively.

■ Compatibility is associated with displacements and strains. This requirement determines that holes or overlap between particles of the material must not exist. In cases where strains are small, it is necessary that the change of displacement throughout the body that has been analyzed must satisfy the following condition:

where ε is a vector that assembles strain elements and is related with the displacement’s element assembled in vector U.

■ The Constitutive Behavior of a material provides a correlation between the two requirements mentioned before as a result of the stress-strain behavior of the material. This can be expressed with the following constitutive equation:

where Δσ and Δε represent the increments of stress and strain respectively, and D is the matrix in which the properties of soil are considered. This is how the non-linear soil behavior is achieved, which is not considered in methods of limit equilibrium.

■ Boundary Conditions represent the geotechnical problem in question. The most important conditions are the imposed displacements, static and/or dynamic applied loads, excavation and construction process, as well as change in pore water pressure.

A comparison between analysis methods, and the fundamental theoretical requirements that they satisfy, are presented in Table 1.

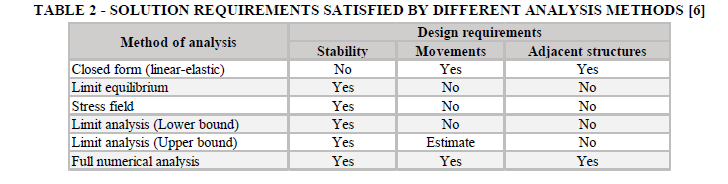
The design requirements depend on the selected method and can vary as shown in Table 2.

 

3. NUMERICAL METHODS 

Numerical methods can be divided in three general groups: Continuum, Discontinuum and Hybrid methods. In the first one, the geometric domain is managed by means of a discretization in a finite number of elements. The solution is then obtained through numerical approximations within differential equations. In discontinuum methods, the geometric domain is managed as a set of interrelated discrete elements. This method is generally used when fractured rock beds are studied. Finally, Hybrid methods are used in rock engineering, where advantages of both methods mentioned before can be applied [7] [5].

Finite elements methods

Finite Element Method (FEM) is part of continuum methods and is used to determine the Factor of Safety (FOS) by two possible procedures [8]: Direct and Improved Limit Analysis methods. In the Direct analysis, slope stability can be evaluated with a shear strength reduction technique or by means of superficial loads increments or mass loads application. For the improved limit analysis, slope stability is determined based on Limit Equilibrium Method (LEM) in addition to the finite element method [9].

This paper emphasizes the shear strength reduction technique. For this purpose, parameters such as the modulus of elasticity, Poisson’s ratio and the dilation angle are needed, besides conventional parameters used in LEM (e.g. internal friction angle and cohesion). These additional parameters can be selected based on existing tables, since the FOS determination is not affected if adopted parameters are within an acceptable range [5]. The direct method offers the following benefits and advantages compared to traditional analysis methods for slope stabilization [9] [6] [10]:

■  Failure mechanism can be found without adopting a failure surface shape or location. Failure mechanism shall develop along zones where the material strength does not withstand the applied stresses.

■  Since the method of slices is not applicable, interslice forces are not necessary.

■  By using real elasto-plastic parameters in the model, FEM provides displacements and deformations values according to real stresses and applied loads through construction process.

■  It is the most appropriate method in terms of modelling progressive failures, for both, initial and final phase.

■  Complex stratigraphy can be easily modeled.

It is possible to consider the soil-structure interaction, in cases where reinforcement structures are required.

 

4. LIMIT EQUILIBRIUM METHODS  

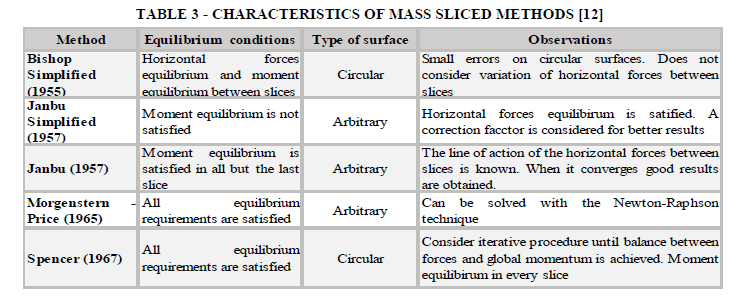
LEM is based on a static analysis between acting and resistant forces acting on a potentially unstable soil mass. Due to their simplicity in comparison to stress-strain based methods, it is known as a low cost and time consuming method, thereby it is widely used. Within this method two categories can be distinguished [11]. The first is used only when the geometry of the slope is simple enough to be considered as planar rupture and wedge rupture. In addition, it provides an exact solution considering the absence of deformations and a constant FOS throughout the entire failure surface. Thus, the global equilibrium is analyzed considering a single sliding mass in homogeneous soils. The second category tends to be hyperstatic due to the complexity of the geometry and requires some simplification to obtain a solution. The second method divides the mass into vertical slices so that each one has its respective two-dimensional equilibrium analysis. This analysis can be performed on complex geometries with different materials, external loads and interstitial pressures [11]. The method of slices can be divided into precise and approximate methods. Approximate methods do not satisfy all equilibrium equations, meanwhile the precise method does. The slice methods used in this paper are presented in Table 3 according to their different characteristics.

 

 

5. FACTOR OF SAFETY 

FOS is used to determine the level of threat for an exposed slope and considers its behavior under unfavorable conditions. FOS is defined in various ways, most of them are based on the equilibrium study of an element and the forces acting on it. Likewise, it is defined as the relationship between the shear resistance of the existing materials in the slope and the critical stresses produced by a potential failure surface. This can be expressed as follows [13]:

When it comes to circular surfaces where resistant and acting moments are involved, the previous equation takes the form of:

Most FOS analysis methods are based on the Coulomb failure criterion, where an equilibrium is satisfied along a given failure surface. This surface can be analyzed as a block or it can be divided into slices, in which case the equation is analyzed for each of the divided parts. As a result, the FOS equation can be expressed as:

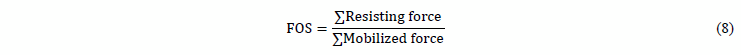
For FOS values less than one, there is a possibility that the slope might collapse. For this reason, it is recommended to adopt safety margins that provide a slope inclination defined by a FOS greater than one.

 

6. CASE OF STUDY

When is about natural phenomena like landslides and floods, La Paz is the most vulnerable city in the country, due to either natural or socio-natural reasons. Its topography and soil composition, as well as the uncontrolled growth of the urban area increases the seriousness of these phenomena and can decrease the period of time between them [14].

The area of the study is within the 41% of urban sprawl, located inside moderate risk areas, which means that abrupt to moderate natural slopes are present. It is also affected by superficial and internal erosion, unstable sectors caused by the saturation and decrease of physical-mechanical characteristics, and the presence of potentially active fault zones [15].

In 2011, the Municipal Autonomous Government of La Paz (GAMLP) presented the Risk Map, determining which geographical areas presented the possibility of adverse events. The Risk Map is based on natural characteristics of the terrain, such as topography, geology, active geological faults and soil geomechanically conditions and takes into account the social, political or economic system that will be affected [15].

According to the Risk Map, the area of Villa Exaltación presents a high geo-hazard level and a moderate level of vulnerability, bearing in mind that the hazard is the combination of external adverse factors caused by natural origins as a result of human intervention for specific places; vulnerability could be considered as the situation in which a population finds itself facing hazards [15].

In June 2014, Antea Belgium Group and Universidad Mayor de San Simón UMSS presented the results of a study called “Gestión Integral de la Cuenca Alpacoma” that was conducted from March to September of 2013. The study comprises different analyses and tests within Alpacoma since it has become a recurrent risk zone for the past 15 years.

Complementary studies were also executed by the National Service of Geology and Mining (Sergeotecmin) in 2005, the Soil Mechanics Laboratory of UMSS in 2013 and Maldonado Exploraciones in 2012.

6.1 Location

The studied natural slope is located in the southeast area of the city El Alto, on the border between the area of Villa Exaltación and the upper sector of Alpacoma’s river basin, covering an approximate extension of 6500 m². The area has a cold climate with temperatures below 0°C and maximum precipitation between the months of October and April, a period in which 90% of precipitation occurs. The average of evaporation reveals that these are dry areas with high values of solar radiation [3].

6.2 Topography and geology 

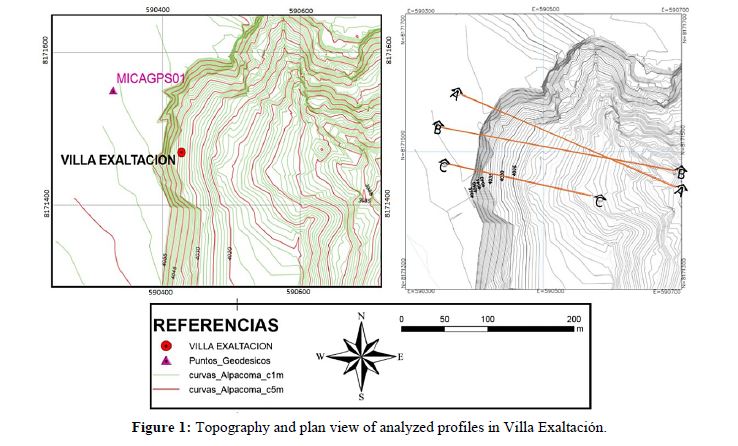
The topography is characterized by the presence of well-defined scarps along the entire analyzed profile in a constant and almost regular manner. For this reason, the decision was made to conduct a representative analysis of three profiles. These profiles are located at the beginning and end of the longitudinal scarp contour, and where the least distance between the scarp and the adjacent avenue prevails.

Regarding the geology of the area, eight types of units can be distinguished. Three of them persist along the profiles: Formación Milluni (Qmi), Formación La Paz (Nlp) and a colluvium material unit defined as Deslizamiento (Qdzl). The first strata is made up of poorly graded or well graded gravel on the slope border; the second, characterized silty sand (SM) material and a combination of silty sand and clayey sand (SM-SC) with sporadic levels of fine gravel and coarse sand. Finally, the presence of colluvial deposits as a result of advanced erosion. In addition, traction cracks were identified, acting as indicators of possible active movements due slope instability.

6.3 Geotechnical studies conducted

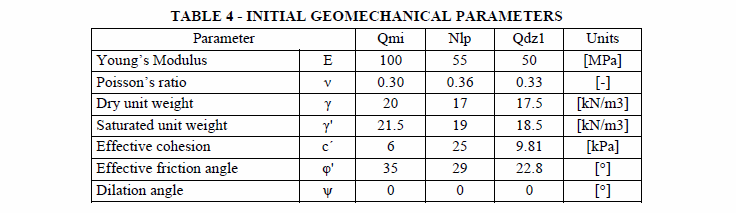
Collected information relevant to the area of study includes sieve granulometry tests, Atterberg limits, hydrometer test and direct shear tests. The tests mentioned were analyzed and supplemented in order to obtain the initial geomechanical parameters needed to start the modeling process in Plaxis. Geomechanical parameters adopted for each stratum are presented in Table 4.

From this information it is determined that Formación Milluni (Qmi) is composed of granular materials, which are fundamentally sandy gravel with bolts, presenting a low level of plasticity. On the other hand, as it is a well-graded soil, it has an acceptable and favorable permeability to carry out a long-term analysis under drained conditions.

Tests reveal that Formación La Paz (Nlp) soil’s composition consists mostly of low to medium plasticity clays, and also lesser clayey and silty sands. According to its classification, this type of soil has a regular permeability and workability. Additionally, information has been collected from direct shear tests to obtain residual parameters since it is close to Alpacoma River where traction cracks have been identified.

Material Deslizado (Qzdl) consists of granular materials like sandy gravel with pebbles and boulders. Moreover, their characteristics and properties are similar to Qmi, therefore it can be deduced that this material formed part of the mentioned unit before the material motion.

 

 

7. CALIBRATION OF GEOMECHANICAL PARAMETERS

Starting with initial geomechanical values, final parameters are then calibrated in Plaxis. For this purpose, A-A Profile is used for the base model process. In Figure 1, the site topography and delineated profiles are shown.

Firstly, profile geometry was introduced and then the stratums that compose the geometry were defined. Once this information was introduced, geomechanical parameter values of each unit were assigned.

Next boundary condition is water table delineation. Due to the limited information about the specific area of analysis, an assessment was made upon the groundwater presence in Tejada Alpacoma landslide, which is located 200 meters away from the area of the study and presents the same geological units and similar soil composition. Thus, the most critical situation for the slope analysis considers a 25 meter depth water table that follows similar slope inclination.

For the next step, three calculation phases were defined:

■ The first, in which initial conditions are considered by a plastic calculation and a type of load called Total Multiplier, allows the software to provide the initial stresses of the soil. A linear elastic model is assigned to the material, only for this phase.

■ The second, which continues with a plastic calculation and a type of load called Staged Construction, provides existing deformations in the slope as a result. In this stage, Mohr Coulomb failure model is applied.

■ The third and most important phase calculates FOS values. In this phase, the Phi/c reduction method is assigned along with a type of load called Incremental Multipliers.

The iteration process involves finding the geomechanical parameters that meet a FOS=1, simulating critical conditions; therefore, these parameters would be the minimum ones that might make the slope stable.

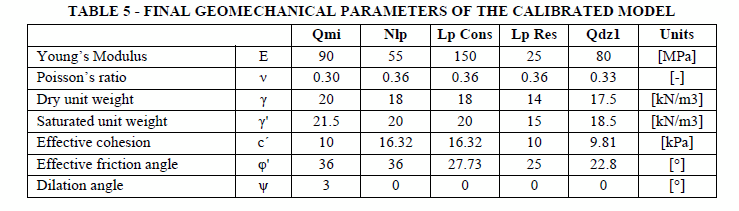
During first iterations, geometry was adjusted in order to obtain congruent boundary conditions for the initial model, increasing the analysis depth in such a way that a stratum called La Paz Consolidada (Lp Cons) was introduced and defined. La Paz Consolidada represents the conditions of a consolidated stratum considering the depth at which it is located and adopts a modulus of elasticity slightly greater than Nlp. 

Due to traction cracks presence within the area, it is assumed that a previous failure existed; thereby, part of the Qmi material was displaced and ended up forming the Qdz1 unit. Hence, the stability problem focuses on Nlp strata and an additional stratum called La Paz Residual (Lp Res) is incorporated. Residual geomechanical parameters are assumed for Lp Res.

The cohesion for Qmi had to be slightly increased since initial values did not represent the current stable situation of the stratum.

All of these adjustments were needed for the first step of calibration, which focuses on finding the failure plane. Next step is about redefining the failure surface by means of reducing soil parameters values. In this way, the geomechanical parameters found are the minimum values that might represent the current slope state.

As previously established, Nlp and Lp Res parameters were the most influenced after iterations; cohesion and friction angles are considered the most important parameters for achieving the desired behavior of the slope. After iterations, values changed depending on elasticity modulus; going from very weak to very rigid clays. A quite low module of elasticity would not match with the actual situation; furthermore, very high values dissolve the possibility of any failure, then results were filtered until the minimum relevant values were found according to slope expected behavior. 

A very important parameter introduced during the final calibration phases is the dilation angle. Due to the fact that Qmi is composed of granular soils and a shear deformation exists, the soil expands, and the friction angle tends to be affected. In Table 5, the results of the final parameters of the calibrated model are shown.

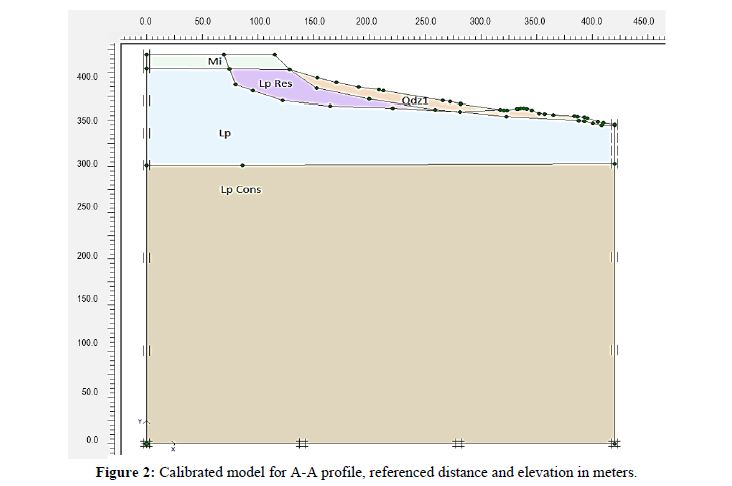
Figure 2 shows the final geometry of the calibrated model in Plaxis that belongs to profile A-A.

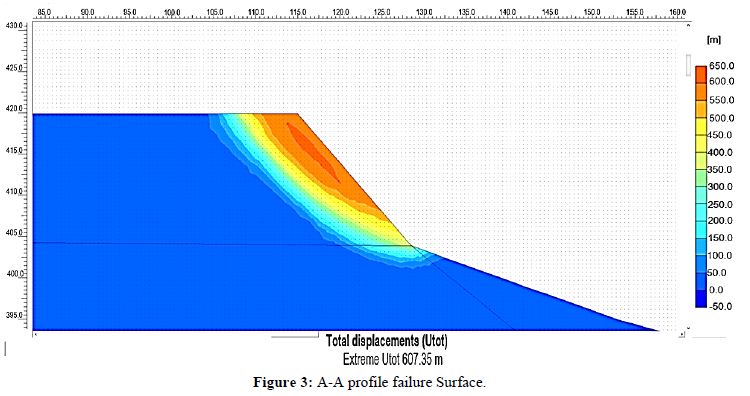
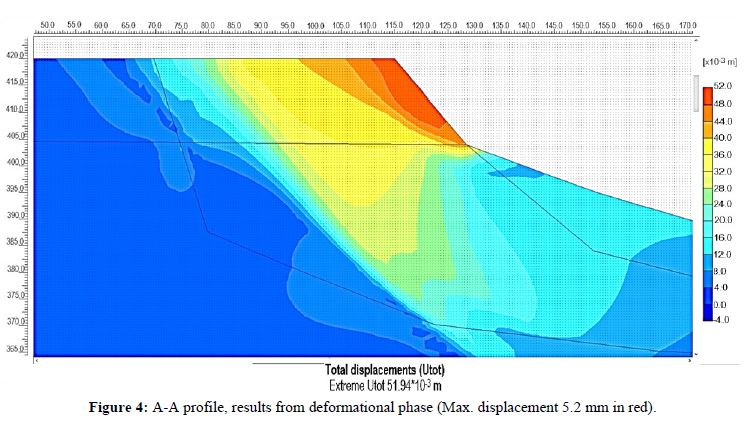
With calibrated model of A-A profile, FOS of 1.03 was obtained, Figure 3 displays the failure surface and Figure 4 the maximun displacements for the same profile. Maximum displacements for A-A calibrated profile reached values of 5.2 mm. Once the calibration stage was done, the evaluation of solution alternatives were the next step.

 

Once the calibrated model results were obtained, soil parameters were verified for both B-B and C-C profiles by introducing each profile’s geometry ans phreatic level. For these profiles calibrated values from the different strata were used (Table 2) for initial modelling.

A FOS = 0.88 was obtained for the B-B profile along with a maximun displacement of 2.57 cm under critical considerations with a high phreatic level and Lp Res strata. These values exhibit that if critical conditions may remain, the slope would not be capable to resist acting forces, leading to failure. A new analysis was conducted under no-critical considerations in order to verify if actual soil parameters give stability to the slope; thereby, FS=1.15 was obtained as a result.

Similar behaviour was observed within C-C profile, where a FOS = 0.82 was obtained under critical conditions along with 15.2 cm of total displacements. And FS=1,03, total displacement of 1.9 cm were calculated by means of natural condition verification. 

Once, the three calibrated models were analysed under natural conditions, some posible solutions of stability were studied.

 

8. STABILITY ALTERNATIVES

The most suitable stabilization methods are those that besides reaching slope stability are the most economically efficient. As before mentioned, the evaluation zone is part of priority stabilization sectors. There is a vast quantity of zones within Alpacoma’s river basin that needs analysis and remediation; for such purpose simple up to complex remediation works were considered under the scope of this study. Some characteristics were examined within the area: low population downhill, low traffic in the upper part of the slope; the main scarp is surrounded by a fence which is 8-meter distance from the scarp towards the avenue. Besides, some watershed management works were observed such as plants close to the toe zone. Residential structures are about 400 meter distance from the toe. 

8.1 A-A PROFILE

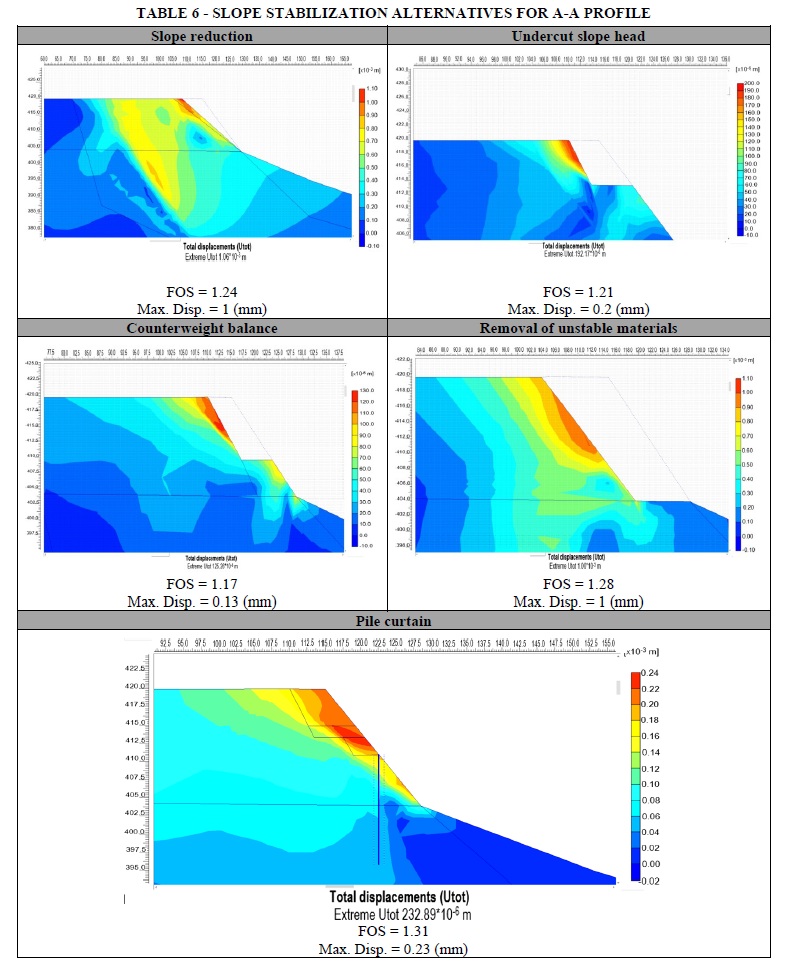
Table 6 displays deformational phases along with FOS results for the slope stabilization analysis of different alternatives, modelled for A-A profile.

Even though the five presented alternatives (Table 6) accomplished minimum safety values, only head undercut and pile curtain were analyzed for B-B and C-C profiles. These are the reasons why the other alternatives were not further considered: 

■ Slope reduction might be an interesting alternative in terms of reaching minimum FOS and deformations; nonetheless, new considerable deformations were observed at a 15-meter span from the scarp. Thereby this alternative was discarded. 

■ Counter weight balance gives the least deformations among the rest of the alternatives and a FOS > 1; nevertheless, this solution requires more resources to be implemented such as a top undercut and the compaction of selected material to form a type of berm that will provide the counterweight balance as toe support.

■ Unstable materials removal is a prevention method that might be used is situations where is the only way to reduce the area vulnerability. Due to the great material amount, product of excavation, this alternative was discarded.

For the slope undercut a 5 meter span is needed and materials shall be removed until 6 meter depth, giving a geometry with 62° inclination from the horizontal plane.

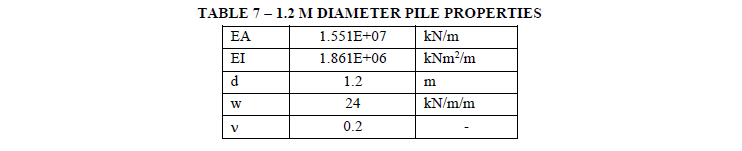
Pile curtain for A-A profile is composed by tangent piles with 1.2 m diameter and 16 meters length. The most efficient location for placing the pile curtain is at the toe, by this means piles will pass through the most competent strata. Concrete compressive strength should be 210 Kg/cm² along with other properties specified in Table 7.

8.2 B-B Profile

Once alternative stability solutions were studied for A-A profile, then profile B-B response was analyzed by means of critical conditions and considering the two above mentioned alternatives.

For slope undercutting within B-B profile, a 5-meter span excavation is needed with 4-meter depth, reaching a 64°slope.

Regarding to the pile curtain, it was determined that the optimum position was one meter deeper than profile A-A location. Besides the contention line, undercutting will be needed as well, at least a 3-meter wide and 4-meter depth cut from the scarp, in order to reduce earth pressure over the curtain and slope stability.

The results from the deformational phase modeling are shown in Table 8 along with FOS values for both alternatives. 

8.3 Profile C-C

The alternatives for C-C profile were verified for the undercutting and pile curtain. It was determined that a 5 meter wide and 8 meter depth excavation is needed at the top part, in order to have a 63° inclination referred to the horizontal plane. For the pile curtain, optimum location is two meters deeper compared to profile A-A, a 3 meter wide by 4 meter depth excavation shall be needed at the head of the slope for stability purposes. The results from the displacement phase calculus are shown in Table 8 with respective FOS values.

According to the results, it is important to remark that maximum displacements were minimal and FOS values were similar for both alternatives; thereby, the head undercut is the best alternative since execution time and costs are less compared to the pile curtain execution, this alternative accomplishes stabilization issues and diminishes the sliding hazard in the zone.

For B-B and C-C profiles, displacements are also minimal; however, FOS is quite close to the permissible FOS values but still slightly below 1.2. It is important to remark that Plaxis modelling is more a strain-dependent slope stability method. Thus, verification was complemented in accordance with Limit Equilibrium Method.

 

9. VERIFICATION BY MEANS OF LIMIT EQUILIBRIUM METHOD

LEM is a widely used method for soil stability analysis; thereby, FOS values were recalculated through Bishop simplified, Morgenstern-Price, Janbu’s Simplified, corrected Janbu and Spencer methods, SLIDE software was used for such purpose.

It is important to realize that LEM method does not need a model calibration and requires less soil parameter’s information like cohesion, friction angle and bulk unit weights. For this purpose, the used soil’s parameters correspond to the calibrated parameters applied in PLAXIS, for all the profiles.

According to the Geotechnical Manual for Slopes, the Spanish Edification Technique Code CTE [16] and risk factors previously defined, Villa-Exaltacion slope presents a minor life risk and low economical risk; thereby, the minimum FOS value shall be 1.2 in order to guarantee slope stability.

LEM results for each profile are shown in Table 9. The modelled solution corresponds to the head undercut slope, since this was the most optimal solution previously defined.

 

 

10. CONCLUSIONS

Finite Element method was applied for Villa-Exaltacion slope stability analysis. For this purpose, a calibration process was done based on parameters reduction criteria. Initial adopted parameters were reduced until failure was reached (FOS=1), by means of several iterations. According to the soils’ characteristics, some behavior criteria were assumed in order to get the failure plane and a successful calibration.

Safety factors were calculated by means of real conditions modelling after calibration, critical FOS values were 1.03, 0.88 and 0.82 within the three studied profiles. Thereby, mitigation works are precisely needed since the sector is catalogued as high geo-hazard zone. Different stabilization alternatives were analyzed, such as head undercut slope, removal of unstable materials, counterweight at the toe and tangent piles curtain. It is been deduced that deformation results are adequate (varying from 0.2 mm up to 5.6 mm). In order to verify Plaxis results, Limit Equilibrium Method was used, and FOS values were above 1.2, minimum value required from guidelines as CTE. It was concluded that major complexity stabilization works might not be needed since the head undercut slope would resolve stability problems. Thereby, undercut slope is the most efficient stability solution compared to other alternatives such as the implementation of tangent piles curtain.

Numerical methods are characterized by focusing on stress-strain reduction rather that FOS numerical value, representing a more exact modelling method when slope analysis is needed. For the present study, Finite Element method is merely based on the stress-strain response of the materials giving more conservative and representative results, since this method is not only based on statics analysis like LEM.

 

11. REFERENCES

[1] L. González de Vallejo, M. Ferrer, . L. Ortuño y C. Oteo, Ingeniería Geológica, Madrid, España: Pearson, 2002.

[2] F. Viscarra, «Slope Stability Analysis for Landslide Probability Mapping within Pampahasi Zone, La Paz - Bolivia,» de XV Panamerican Congress of Soil Mechanics and Geotechnical Engineering Proceedings, Buenos Aires - Argentina, 2015.

[3] UMSS y Antea Group, «Plan de manejo integral para la cuenca Alpacoma de Bolivia,» Tomo 4, 2015.

[4] M. De Vos and V. Whenham, "Workpackage 3 Innovative design methods in geotechnical engineering," Belgian Building Research Inst., GeoTechNet-European Geotechnical Thematic Network.

[5] J. Bojorque-Iñeguez, «Métodos para el análisis de la estabilidad de pendientes,» MASKANA, vol. 2, nº 2, 2011.

[6] D. Potts, «Numerical analysis: a virtual dream or practical reality?,» Géotechnique, vol. 6, nº 535-573, p. 537, 2003.

[7] E. Eberhardt, D. Stead and J. Coggan, "Numerical anañysis of initiation and progressive failure in natural rock slopes-the 1991 Randa rockslide," International Journal of Rock Mechanics and Mining Sciences, vol. 41, no. 1, pp. 69-87, 2004.

[8] D. Naylor, Numerical Methods in Geomechanics, Braga: Springer Netherlands, 1982.         [ Links ]

[9] T. Matsui and K.-C. San, "Finite Element Slope Stability Analysis by Shear Strength Reduction Technique," Soils and Foundations, vol. 32, no. 1, pp. 59-70, March 1992.

[10] H. Zheng, . D. Liu and C. Li, "Slope stability analysis based on elastoplastic finite element method," International Journal for Numerical Methods in Engineering, vol. 64, no. 14, 21 July 2005.

[11] Instituto Geológico y Minero de España (IGME), Manual de Taludes, 1987.         [ Links ]

[12] E. A. Pérez, «Estabilidad de Taludes,» Catalunya, 2005.        [ Links ]

[13] J. Suarez, «Capítulo 4: Análisis de Estabilidad,» de Deslizamientos: Análisis Geotecnico, Bucaramanga, Geotecnología S.A.S., p. 130.

[14] A. Cuevas, «Página Siete, Diario Nacional Independiente,» 19 Enero 2019. [En línea]. Available: https://www.paginasiete.bo/sociedad/2014/1/19/anos-registro-menos-deslizamientos-11761.html. [Último acceso: 2 Octubre 2017].

[15] G. Sistema Alerta Temprana Ante Inundaciones y Deliz, «Diagnóstico General del Sistema de Alerta Temprana,» GAMLP, La Paz, 2011.        [ Links ]

[16] Ministerio de Vivienda de España, «Código Técnico de la Edificación,» 2006.        [ Links ]