http://dx.doi.org/10.23881/idupbo.018.1-5i

 ARTÍCULOS – INGENIERÍAS

 

ESTIMACIÓN DE INTENSIDAD DE LLUVIA PARA ESTUDIOS DE PROPAGACIÓN RADIOELÉCTRICA EN BOLIVIA

 

ESTIMATION OF RAIN INTENSITY FOR RADIO PROPAGATION STUDIES IN BOLIVIA

 

 

Gustavo Siles y Daniel Chirinos

Laboratorio de Radiocomunicaciones

Centro de Investigaciones Ópticas y Energías (CIOE)

Universidad Privada Boliviana (UPB)

gustavosiles@upb.edu

(Recibido el 18 mayo 2018, aceptado para publicación el 10 de junio 2018)

 

 

---

RESUMEN 

La caracterización de la intensidad de lluvia, R_p (mm/h), para estimar la atenuación, A (dB) que produce una precipitación, es de gran importancia dada la relación directa entre ambas variables. Una descripción precisa de R requiere de estadísticas anuales obtenidas a partir de campañas de mediciones pluviométricas de varios años. En ausencia de esta información, es posible utilizar modelos de predicción que permiten determinar la Función de Distribución Acumulada Complementaria, P(R). El presente estudio implementa modelos de predicción propuestos en diferentes versiones de la Recomendación UIT-R P.837 con el objetivo de obtener la función P(R) para diferentes lugares de Bolivia. Los resultados obtenidos llevan a la conclusión preliminar que el modelo propuesto en la última versión de la Recomendación seguiría mejor las características climatológicas de los sitios seleccionados para el estudio.

Palabras Clave: Propagación Atmosférica, Intensidad de Lluvia, Atenuación por Lluvia.

---

ABSTRACT

The characterization of point rainfall rate, R_p (mm/h), with the aim of estimating rain attenuation, A (dB) caused by a precipitation is of primary interest due to the straight relation between both variables. An accurate description of the behavior of R_p needs yearly statistics obtained from long-term pluviometric measurement campaigns. In absence of this information, prediction models allow yearly Cumulated Complementary Distribution Functions, P(R), to be determined. In the present study, prediction models proposed in different versions of the Recommendation ITU-R P.837 have been implemented in order to retrieve P(R) for different sites in Bolivia. The results obtained lead to preliminary conclude that the model proposed in the last version of the Recommendation would better follow the climatic characteristics of the sites chosen for this study. 

Keywords: Atmospheric Propagation, Rain Intensity, Rain Attenuation.

---

 

 

1.     INTRODUCCIÓN 

El estudio del canal de propagación en un sistema de comunicaciones es fundamental para conocer los niveles de potencia, ruido e interferencias presentes en el receptor, los cuales afectan directamente a los parámetros de calidad del sistema. Por ejemplo, condiciones de propagación adversas pueden dar origen a un aumento en la tasa de error de bits (BER) y a un deterioro en la relación señal a ruido (SNR). Ante estos efectos, la disponibilidad del enlace de comunicaciones disminuye y, por tanto, el servicio de comunicaciones al usuario final sufre un deterioro, situación no deseada por ningún operador de telecomunicaciones.

De modo particular, el canal de propagación en sistemas de comunicaciones inalámbricas plantea situaciones más complejas a la hora de estudiarlo. Las características de propagación en el canal pueden variar con el tiempo, i.e. el canal puede comportarse de una manera en un instante de tiempo t₀ y de otra en un tiempo t₀ + t, y con el espacio, i.e. el canal se comporta de una manera en una ubicación, pero de otra en una ubicación diferente. Por tanto, el modelado del canal de propagación en sistemas de radiocomunicaciones, así como la estimación de las pérdidas que se producen en él, debe tener en cuenta elementos de probabilidad y estadística.

En sistemas de radiocomunicaciones satelitales y terrestres que trabajan en frecuencias por encima de 10 GHz, el efecto de la lluvia es el que mayores degradaciones produce sobre un radioenlace [1,2]. Desde un punto de vista de sistema, la presencia de precipitaciones en forma de partículas de agua líquida en el canal de propagación, se traduce en niveles de atenuación que, en caso de ser muy elevada, puede producir pérdida completa de la señal recibida en el extremo receptor. Estos eventos se conocen como desvanecimientos profundos. El diseño apropiado de enlaces, que eviten este tipo de eventos, requiere de modelos de estimación que permitan calcular estadísticas de la atenuación por lluvia producida en el trayecto y en un periodo de tiempo, que típicamente se considera un año. El principal parámetro, que puede ser medido en superficie y que permite caracterizar una precipitación, es la intensidad de lluvia, R (mm/h), por tanto, su medición o estimación mediante modelos es imprescindible para cuantificar los niveles de atenuación por lluvia en un radioenlace y su probabilidad de ocurrencia.

La Unión Internacional de Telecomunicaciones sector Radiocomunicaciones (UIT-R) propone a través de la Rec. UIT-R P.837 [3], un método de predicción de la intensidad de lluvia, R_p (mm/h), con un tiempo de integración de 1-min, que se supera en porcentajes de tiempo, p%, durante un año medio, para cualquier ubicación en la Tierra. De esta manera, es posible obtener la función de distribución acumulada complementaria P(R) de R_p,. A la fecha, la versión 7 de esta Recomendación es la más reciente, pero el uso de versiones previas es aún común en ámbitos de ingeniería.

En este trabajo, se han seleccionado diferentes sitios en Bolivia, con características climatológicas muy variadas, y se ha realizado la estimación de P(R) a partir de diferentes versiones de la Rec. UIT-R P.837. Los resultados que se esperan son relevantes como un primer paso para futuros estudios de radiopropagación en nuestro país. Así mismo, el objetivo de utilizar diferentes versiones, disponibles para descarga gratuita en [4], es estudiar el comportamiento del modelo de estimación de la UIT-R para el caso de Bolivia a lo largo del tiempo, considerando que en la práctica muchos diseños de radioenlaces terrestres o satelitales que se realizan en ingeniería de telecomunicaciones, se hacen a partir de versiones antiguas, con resultados que posiblemente no son los más precisos.

El artículo está estructurado de la siguiente manera: luego de la presente Introducción, la Sección 2 presenta aspectos teóricos para comprender la importancia del parámetro R en estudios de propagación radioeléctrica. La Sección 3 presenta las diferentes versiones de la Recomendación UIT-R P.837 y sus fundamentos. La Sección 4 presenta los emplazamientos que se han utilizado en este estudio y las estimaciones de intensidad de lluvia para cada uno de ellos. Los resultados se discuten en la Sección 5 y finalmente se presentan algunas conclusiones en la Sección 6.

 

2.     FUNDAMENTOS SOBRE ATENUACIÓN POR LLUVIA EN RADIOENLACES 

Una celda de lluvia está compuesta por partículas de agua cuyos diámetros D pueden variar entre 200 μm y 7 mm. El número de gotas n en función de D se puede modelar con una función de distribución de tamaños n(D), a partir de la cual, usando la teoría de dispersión de Mie para calcular la sección eficaz de extinción σ_e, en (mm²), de cada gota con diámetro D, que depende a su vez de la frecuencia y la temperatura, es posible calcular la atenuación por lluvia, A, en dB. El cálculo preciso de A requiere como paso previo obtener la atenuación específica g_r (dB/km) producida por una precipitación, que se calcula de manera exacta mediante (1), y multiplicar por su espesor, h, en (km). Esta aproximación microscópica al cálculo de A es posible a partir de la obtención de medidas experimentales de n(D) [5], si bien esta tarea requiere de instrumentos de medición especializados, como ser disdrómetros laser.

En la literatura se han propuesto funciones empíricas para modelar n(D), como la función de distribución Marshall-Palmer, Law-Parsons, Joss, o Weibull. A partir de estas, la ecuación (1) se aproxima mediante la relación empírica (2), que relaciona la atenuación específica que produce una precipitación con su intensidad R. Fue propuesta inicialmente por Olsen [6], adoptada por la UIT-R [7], y es válida para frecuencias entre 1 y 1000 GHz, donde los parámetros k y α dependen de la frecuencia, polarización y la temperatura media de la lluvia.

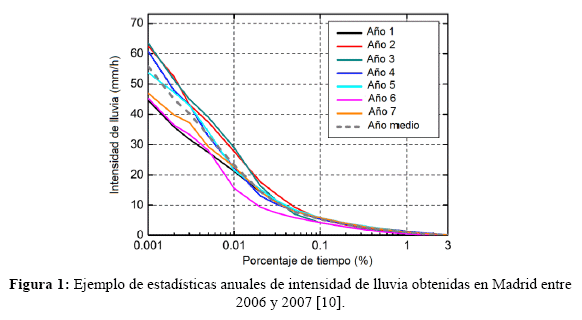
El valor de R en (2) se extrae de la Función de Distribución Acumulada Complementaria anual, P(R), que a su vez se obtiene a través de medidas pluviométricas locales multianuales, con un tiempo de integración de 1-min, o mediante modelos de predicción [3]. Este tiempo de integración permite caracterizar los cambios rápidos que tiene R durante un evento de precipitación y, por tanto, las fluctuaciones temporales de A. La Figura 1 muestra ejemplos de funciones P(R) obtenidas experimentalmente en Madrid [7], a partir de las cuales se puede obtener el valor de R_p que se excede el porcentaje de tiempo p% de un año medio.

De especial interés es el parámetro R_0.01 o intensidad de lluvia que se excede el 0.01% de un año, a partir del cual es posible calcular A_0.01 en radioenlaces terrestres [8] o satelitales [9]. A partir de A_0.01, es posible estimar A_p para cualquier porcentaje de tiempo p% y obtener distribuciones estadísticas de atenuación por lluvia que, desde un punto de vista práctico, interesan a los operadores de telecomunicaciones para analizar la disponibilidad de sus radioenlaces. Sin embargo, obtener experimentalmente R_0.01 a partir de P(R), no es común, pues normalmente las agencias nacionales de meteorología realizan medidas pluviométricas con tiempos de integración mayores, que pueden ir desde una hora hasta datos acumulados diarios, mensuales y anuales. Por tanto, en ausencia de estadísticas locales de intensidad de lluvia de alta resolución, en estudios de radiopropagación se recomienda el uso de la Rec. UIT-R P.837 y su modelo de predicción de P(R). A continuación, se presentan de manera resumida los fundamentos de las versiones P.837-1, -4, -6 y -7, siendo esta última la más reciente. Se han seleccionado estas versiones debido a que en éstas existen cambios mayores realizados por el Grupo de Estudio 3 (SG3) de la UIT-R.

 

3.    MÉTODOS DE PREDICCIÓN DE INTENSIDAD DE LLUVIA DE LA RECOMENDACIÓN UIT-R P.837

3.1  VERSIÓN 1 (1994)

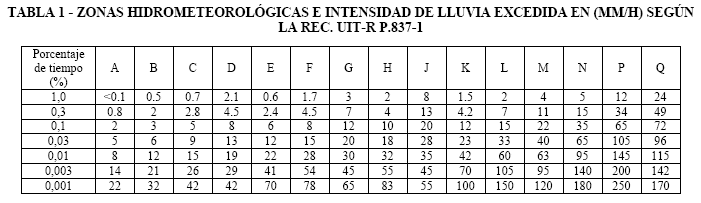
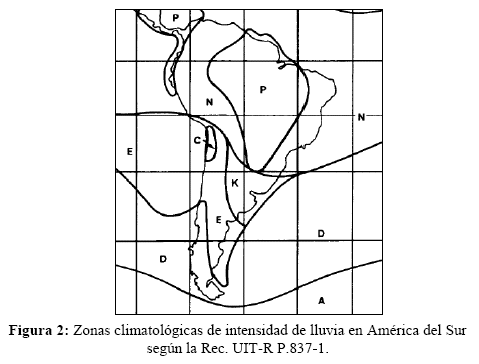
La primera versión de la Recomendación UIT-R P.837 fue publicada el año 1994 y sigue el concepto desarrollado por Crane en [11], que consiste en trazar isogramas que dividen la Tierra en zonas climatológicas con características diferentes de intensidad de lluvia. Siguiendo este método, el modelo de la UIT-R propone una división en 15 zonas climatológicas que se muestran en la Tabla 1, junto con los valores de intensidad de lluvia y los porcentajes de tiempo en los que éstos se superan en un año, que permiten trazar las funciones P(R) similares a las de la Figura 1 para cada zona. La Figura 2 muestra las zonas correspondientes a América del Sur y en particular el caso de Bolivia.

 

Este método, al igual que el de Crane, fue desarrollado en base a datos de registros pluviométricos a nivel mundial, sin embargo, su exactitud está limitada por el número de estaciones que utilizó, su ubicación – generalmente se encontraban en el hemisferio norte -, la cantidad de años de medida disponibles, y la homogeneidad en la resolución temporal utilizada en la adquisición de las medidas. Pese a estas fuentes de incertidumbre, este método es uno de los más utilizados en ingeniería para obtener el valor de R_0.01 y A_0.01.

3.2  VERSIÓN 4 (2003)

Los modelos matemáticos de Predicción Numérica del Tiempo (NWP, Numerical Weather Prediction) permiten la estimación de las condiciones meteorológicas futuras a partir de medidas actuales o registros pasados. Gracias a su uso, es posible generar productos en formas de mapas digitales de variables meteorológicas. En particular, desde un punto de vista de pluviometría, es posible encontrar información sobre la intensidad de lluvia media anual o mensual, la intensidad pico anual, el número de días con lluvia en un año, entre otras variables. Usando productos NWP, la UIT-R propone modelos de intensidad de lluvia global y mapas digitales mundiales de R_p con un tiempo de integración 1-min. y sus respectivas CCDFs.

En la versión 4 de la Rec. UIT-R P.837, la UIT-R desarrolló un modelo global de intensidad de lluvia, utilizando como datos de entrada la base de datos ERA-15 [12] del ECMWF (European Centre for Medium-Range Weather Forecasts). Esta base de datos consiste en productos NWP generados luego del re-análisis de 15 años (enero 1979 a diciembre 1993) de información meteorológica mundial, proveniente en general de la red GTS (Global Telecommunication System) de la WMO (World Meteorological Organization). A partir de esta información, la UIT-R generó mapas digitales de los siguientes parámetros, con una resolución espacial de 1.5°´1.5°:

•  M_S: Cantidad de lluvia media anual estratiforme (mm)

•  M_C: Cantidad de lluvia media convectiva (mm)

•  P_r6: Probabilidad de lluvia cada 6 horas (%)

El procedimiento completo [4] de la UIT-R permite estimar, mediante interpolación bilineal [13], los valores de M_S, M_C y P_r6 en cualquier punto geográfico con coordenadas (Lat, Lon) y posteriormente la probabilidad de presencia de lluvia en un año medio, P₀, y la función CCDF de intensidad de lluvia anual, P(R), a partir de las siguientes expresiones:

      

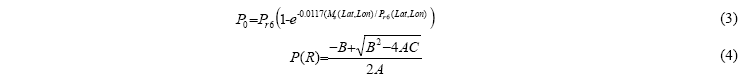
donde

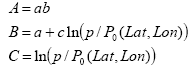
y

 

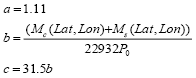
3.3  VERSIÓN 6 (2012)

En la versión 6 de la Rec. UIT-R P.837, el modelo global de intensidad de lluvia propuesto se basa en un conjunto de información de entrada más extenso: la base de datos ERA-40 [14] del ECMWF que consiste en un re-análisis de observaciones meteorológicas de 45 años (septiembre 1957 a agosto 2002). A partir de esta información, la UIT-R proporciona mapas digitales con una resolución espacial mejorada de 1.125°´1.125° de los siguientes parámetros:

•  M_T: Cantidad de lluvia media anual (mm)

•  β: Relación entre la cantidad de lluvia convectiva y cantidad de lluvia media.

•  P_r6: Probabilidad de lluvia cada 6 horas (%)

Estos parámetros pueden ser obtenidos para cualquier punto geográfico con coordenadas (Lat, Lon) usando interpolación bilineal [13]. A partir de los valores M_T y b para el punto de interés, se estiman los valores de M_S y M_C con las siguientes expresiones:

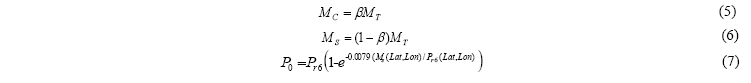
A partir de M_C y M_S y las expresiones (3) y (4) es posible obtener el porcentaje de probabilidad P₀ con (7) y la CCDF de intensidad de lluvia anual P(R), con el cuidado de utilizar el siguiente conjunto nuevo de coeficientes:

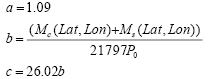
3.4  VERSIÓN 7 (2017)

Como sus predecesores, la versión 7 de la Rec. UIT-R P.837 - en la actualidad la más reciente – es un modelo global para la predicción de estadísticas anuales de R_p con un tiempo de integración de 1-min para una ubicación determinada en la superficie de la Tierra. Para realizar este cálculo el modelo requiere por tanto como datos de entrada:

•  el porcentaje p de tiempo

•  las coordenadas (Lat, Lon) del punto geográfico de interés.

El modelo requiere para su uso de registros mensuales, obtenidos localmente, de lluvia media total MT_i (mm), donde i = 01 a i = 12, y de temperatura media de superficie, T_i (K). En ausencia de esta información, se pueden usar mapas digitales globales de MT_i, cuya resolución espacial es 0.25°´0.25° y obtenidos a partir del análisis de la base de datos GPCC (Global Precipitation Climatology Centre) Climatology V2015 de 50 años (1951-2000) para datos de precipitación sobre tierra, y la base de datos ERA Interim del ECMWF de 36 años (1979-2014) para datos de precipitación sobre agua. Los mapas digitales globales de T_i tienen una resolución espacial de 0.75°´0.75° y se pueden obtener en [15].

El fundamento de este modelo se basa en la necesidad de investigar el impacto de realizar predicciones mensuales de R_p para el diseño de sistemas de radiocomunicaciones y tiene en cuenta 3 suposiciones [16]:

•  Las estadísticas mensuales de R_p, condicionadas a la presencia de lluvia, siguen una ley de distribución del tipo log-normal.

•  El parámetro de forma σ_i de la distribución log-normal es independiente del punto geográfico.

•  La intensidad media de lluvia condicionada a la presencia de lluvia,  (mm/h) depende únicamente de la temperatura media mensual medida a 2 m por encima del nivel de suelo. Esta altura es el estándar recomendado por la WMO para medidas de temperatura de aire.

La siguiente descripción matemática del modelo está basada en el desarrollo presentado en [16]. La función P_i(R) es la CCDF de R del mes i-ésimo y se expresa mediante la función de error complementaria:

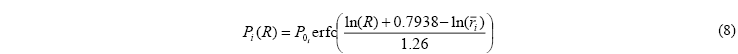
donde es la probabilidad media de lluvia, que se obtiene mediante:

donde N_i es el número de días que tiene el mes i-ésimo (con N₂ = 28.25) y es la cantidad de lluvia total mensual.

La función P(R) es la CCDF anual de R se obtiene combinando las distribuciones mensuales de la siguiente manera:

El valor de  en (9) se obtiene mediante la ecuación (11).

 

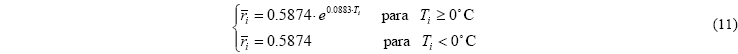
4.     DESCRIPCIÓN DE LOS SITIOS SELECCIONADOS 

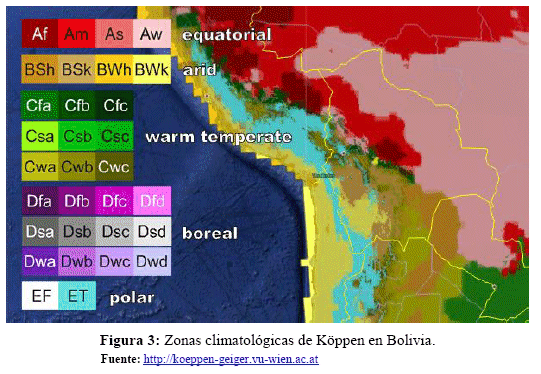
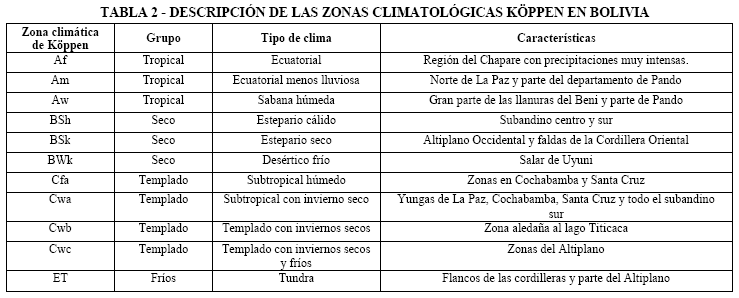
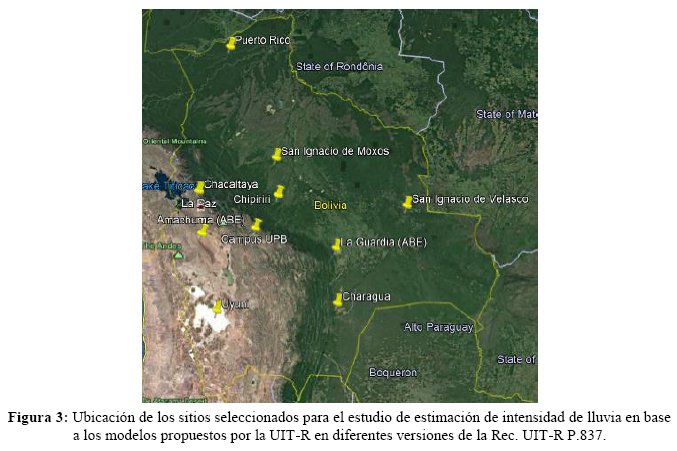
Bolivia presenta una gran variedad de zonas climáticas a lo largo de su geografía, como se puede evidenciar si se analiza la clasificación climática de Köppen para el caso de Bolivia (Figura 3). Este sistema es el más utilizado para la clasificación del clima en la Tierra, donde se definen diferentes zonas climáticas, codificadas en base a un código de 2 o 3 letras [17]. La Tabla 2 presenta un resumen de las zonas climáticas que se pueden encontrar en Bolivia. Puede observarse que al menos un 60% del territorio corresponde a climas tropicales, y en particular, la zona Af que se caracteriza por tener altas precipitaciones durante el año, prácticamente sin épocas secas. En el otro extremo, se observan climas áridos y regiones templadas, con características marcadas de estacionalidad.

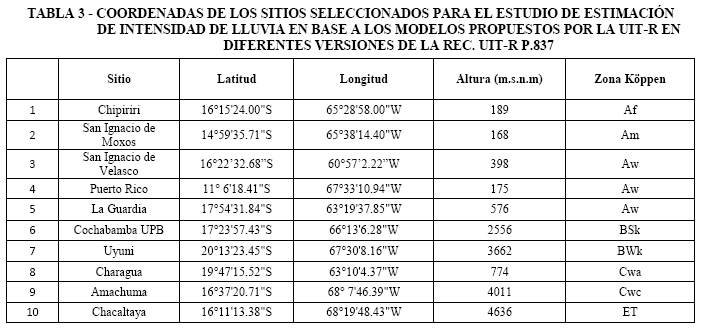
Se han seleccionado 10 sitios para el presente estudio cuyas coordenadas se presentan en la Tabla 3 y que, para referencia del lector, se han identificado sobre un mapa que se observa en la Figura 3. La mitad de los sitios seleccionados corresponden a zonas tropicales con mayor presencia de precipitaciones a lo largo del año. En particular, se debe destacar la zona de Chipiriri (zona Köppen: Af), localidad donde se presentan lluvias acumuladas anuales de hasta 4000 mm [18], las más elevadas en Bolivia. Los 5 sitios restantes corresponden 2 a climas templados, 2 a climas secos y 1 a clima frío. La altitud de los sitios seleccionados es también diversa, propias de la geografía boliviana, con una diferencia entre el sitio más bajo (San Ignacio de Moxos) el más alto (Chacaltaya) de 4468 m. Por otro lado, existen sitios seleccionados debido a razones específicas como ser: a) Cochabamba UPB, situado el campus de la Universidad Privada Boliviana, donde el Laboratorio de Radiocomunicaciones tiene previsto realizar medidas pluviométricas de alta precisión con un tiempo de integración de 1-min, b) Amachuma, donde se encuentra la Estación Terrena de Control principal del satélite de comunicaciones boliviano TKSat-1 que opera en las bandas C, Ku y Ka, y c) La Guardia, donde se encuentra la Estación Terrena de Control de respaldo del satélite de comunicaciones TKSat-1. Ambas estaciones terrenas son operadas por la Agencia Boliviana Espacial (ABE).

 

 

5.     RESULTADOS

Los modelos de estimación descritos en la Sección 4 se implementaron en sendos programas en MatLab^®, con el objetivo de obtener a la salida  de cada uno de ellos el valor de R_0.01 y la función P(R). Los programas requieren para su uso los siguientes parámetros de entrada:

•  Rec. UIT-R P.837-1: Latitud y Longitud

•  Rec. UIT-R P.837-4, P.837-6 y P.837-7: Porcentaje de tiempo, Latitud y Longitud

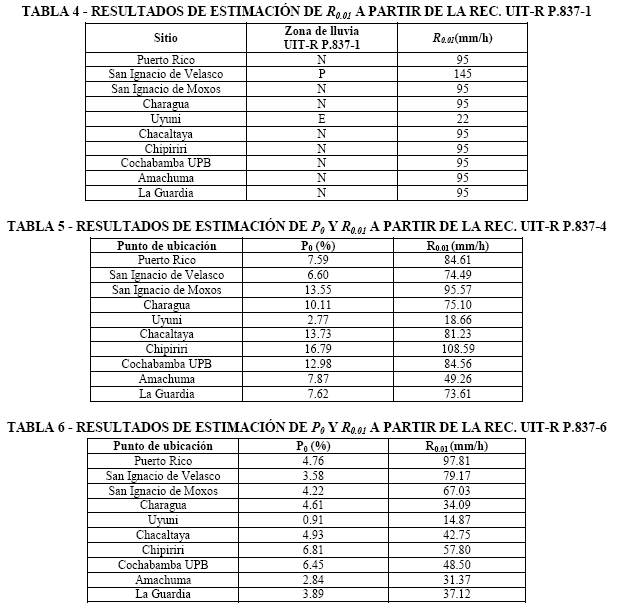
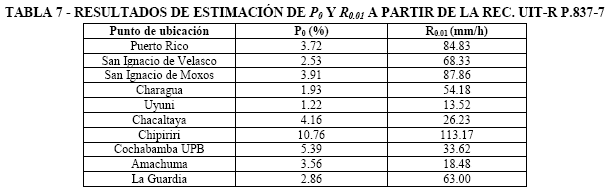
En la Tabla 4 se pueden ver los resultados de R_0.01 obtenidos utilizando la versión P.837-1. El uso de los isogramas agrupa a 8 de los 10 sitios en la zona de lluvia N, donde R_0.01 es 95 mm/h. Por tanto, según este método de predicción, sitios con características climáticas tan diferentes como Chipiriri o Amachuma, tendrían la misma distribución P(R), lo cual en la realidad no es posible. Conclusiones similares pueden obtenerse al comparar, por ejemplo, Puerto Rico con Cochabamba UPB. Por otro lado, la presencia de una zona con altas precipitaciones anuales como Chipiriri no queda en evidencia en la Tabla 4 y sería San Ignacio de Velasco la región con una intensidad de lluvia mayor.

Las Tablas 5, 6 y 7 presentan los resultados de probabilidad de presencia de lluvia estimada en un año medio, P₀, y el valor de R_0.01 con las versiones P.837-4, P.837-6 y P.837-7, respectivamente. En primer lugar, la versión P.837-4 presenta en general valores más elevados en ambos parámetros respecto a la P.837-6. El origen de esta diferencia se podría deber a que la base de datos ERA-15 de ECMWF tiende a sobreestimar el parámetro de lluvia total media anual, M_T, sobre todo en regiones tropicales y ecuatoriales [19, 20], lo cual incide directamente sobre los valores de P₀ y R_0.01. Por ejemplo, en casos como Chacaltaya el valor de R_0.01 = 81.23 mm/h es inusualmente elevado e irreal.

Según [21], el trabajo realizado para ajustar el parámetro M_T de la base de datos ERA-40, evaluándolo con los de otros productos meteorológicos (GHCN, GPCC, GPCP) y de observación de la Tierra (TRMM), permitiría reducir la sobreestimación, lo cual se puede observar si se comparan los resultados de las Tablas 5 y 6 para todos los sitios, con excepción de Puerto Rico y San Ignacio de Velasco. Por otro lado, la estimación de R_0.01 = 57.80 mm/h para Chipiriri es un valor bajo dado que, como se ha mencionado anteriormente, esta región debería presentar los niveles más elevados de todos los seleccionados en este estudio. Estudios de propagación realizados en zonas tropicales con altos niveles de precipitación [22,23], han mostrado que la versión P.837-6 subestima los valores de R_0.01 respecto a medidas pluviométricas experimentales. Esta observación podría explicar el valor estimado de R_0.01 en Chipiriri.

En [24], se destacan las mejoras en la precisión de la versión P.837-6 a nivel global, sin embargo, se enumeran también una serie de limitaciones de la metodología de cálculo, la cuales, a la fecha, se habrían reducido con la reciente introducción de la versión P.837-7. Los resultados que se presentan en la Tabla 7, muestran que los valores de R_0.01 estimados con esta versión son, a priori, razonables en relación a las zonas climáticas de cada uno de los sitios. Un ejemplo de esta observación, son Chipiriri (R_0.01 = 113.17 mm/h) o Chalcaltaya (R_0.01 = 26.23 mm/h). Por otro lado, los sitios con climas tropicales (zonas Köppen: Af, Am y Aw) presentan en general valores de R_0.01 > 60 mm/h, por encima de los observados en otros sitios. 

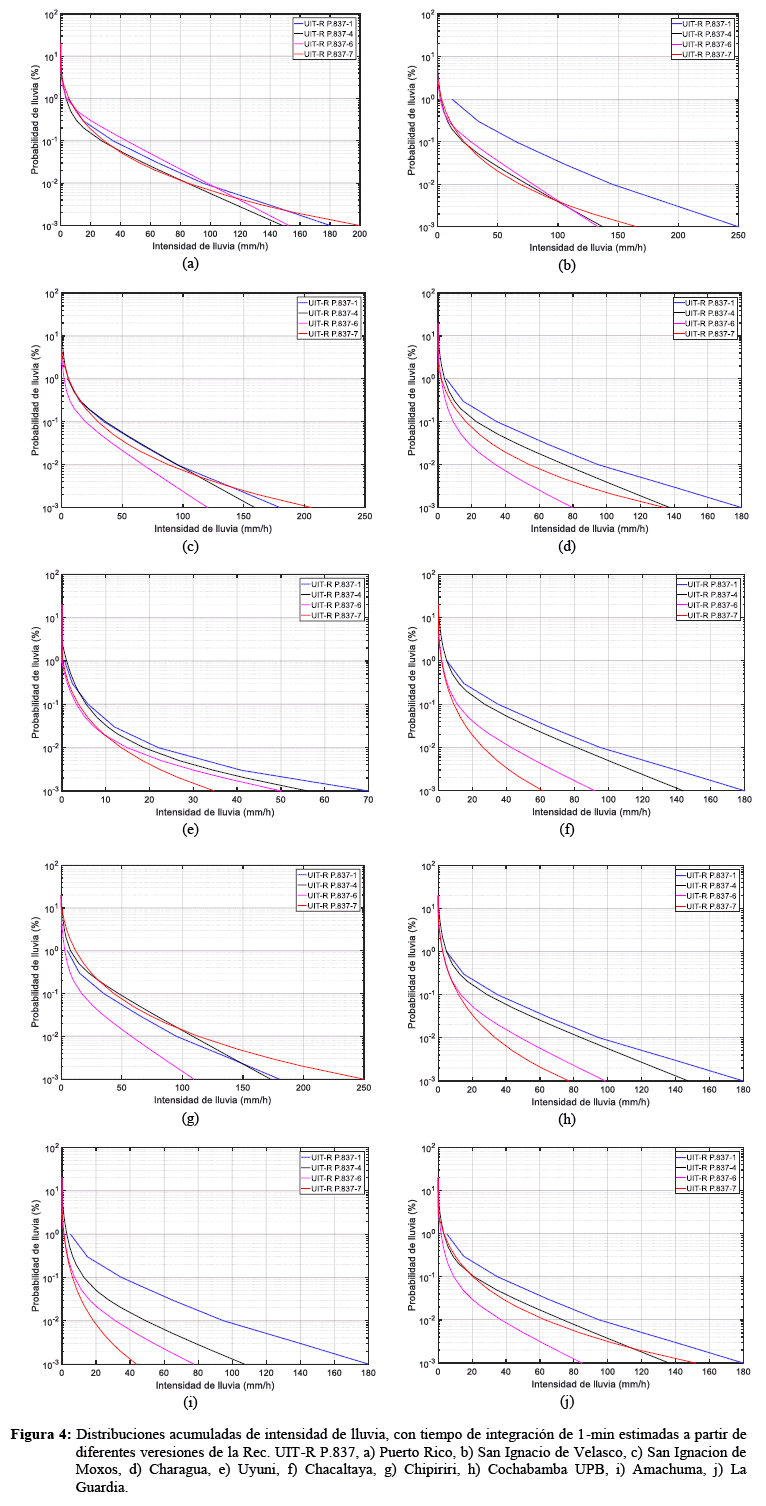
Finalmente, en la Figura 4 se presentan los resultados de las funciones P(R) estimadas para cada uno de los sitios con cada de unas de las versiones. Se observa que los resultados en general tienden a diferir entre las versiones, lo que es esperable dadas las diferentes aproximaciones para el modelado de P(R) en cada versión. Por otro lado, estas curvas estimadas deben ser contrastadas en futuras etapas de esta investigación con mediciones pluviométricas de larga duración, por ejemplo, en el sitio Cochabamba UPB donde pueden operarse instrumentos de medida y garantizar así una alta calidad, así como disponibilidad, de las medidas.

6.     CONCLUSIONES

El presente estudio constituye una primera aproximación al estudio de la intensidad de lluvia, R,  para aplicaciones de radiopropagación en Bolivia, tanto para enlaces terrestres como satelitales que trabajen por encima de 10 GHz. Con este propósito, se han estudiado diferentes versiones de la Recomendación UIT-R P.837 e implementado los modelos de predicción de la función de distribución acumulada P(R) y, a partir de ésta, el valor de R_0.01 para diferentes sitios en Bolivia. Estos sitios fueron seleccionados analizando sus características climáticas según el sistema de clasificación de Köppen.

Los resultados obtenidos conducen a la observación preliminar que la versión P.837-7 podría describir mejor las características pluviométricas de los sitios seleccionados. Esta afirmación se basa enteramente en las zonas climáticas a las que pertenece cada sitio y las características de lluvia que, en principio, existen en ellas. Sin embargo, a fin de validar esta afirmación, es necesario analizar o realizar medidas pluviométricas de larga duración en Bolivia, preferentemente obtenidas con un tiempo de integración de 1-min. Por otro lado, en relación a versiones previas de la Recomendación, se ha evidenciado que el uso de isogramas de la versión P.837-1 no describen adecuadamente ni con precisión la intensidad de lluvia en Bolivia, y que las versiones P.837-4 y P.837-6 presentan inconsistencias para sitios específicos.

 

7.     AGRADECIMIENTOS

Los autores agradecen al Prof. Carlo Riva del Politécnico de Milán por su colaboración para la implementación de las versiones de la Rec. UIT-R P.837. El presente trabajo forma parte del proyecto MeteoBol, financiado por la Universidad Privada Boliviana.

 

8.     BIBLIOGRAFÍA

[1] G. Maral, M. “Bousquet, Satellite Communications Systems,” John Wiley&Sons, pp. 193, 2009.

[2] H. Lehpamer, “Microwave Transmission Networks,” McGraw-Hill, pp. 54, 2010.

[3] ITU-R Recommendation P.837-7, “Characteristics of precipitation for propagation modelling,” 2017.

[4] URL: https://www.itu.int/rec/R-REC-P.837/en. Último acceso: 07/05/2018.

[5] J. M. Garcia-Rubia, J.M. Riera, A. Benarroch, P. García-del-Pino, “Estimation of Rain Attenuation From Experimental Drop Size Distributions,” IEEE Antennas and Wireless Propagation Letters, Vol. 10, Nº 3, pp. 839-842, 2011.

[6] R. Olsen, D. Rogers, D. Hodge, “The aR^b relation in the calculation of rain attenuation,” Antennas and Propagation, IEEE Transactions on, Vol. 26, Nº 2, pp. 318-329, 1978.

[7] ITU-R Recommendation P.838-7, “Specific attenuation model for rain for use in prediction methods,” 2005.        [ Links ]

[8] ITU-R Recommendation P.530-17, “Propagation data and prediction methods required for the design of terrestrial line-of-sight system,” 2017.        [ Links ]

[9] ITU-R Recommendation P.618-13, “Propagation data and prediction methods required for the design of Earth-space telecommunication system,” 2017.        [ Links ]

[10] J. M. Garcia-Rubia, J.M. Riera, P. García-del-Pino, G. Siles, A. Benarroch, “Experimental assessment of slant-path rain attenuation variability in the Ka-band,” International Journal of Satellite Communications and Networking, Vol. 34, Nº 2, pp. 155-170, 2015.

[11] R. K. Crane, “Prediction of attenuation by rain,” IEEE Trans. Commun., vol. COM-28, pp. 1717–1733, Sep. 1980.

[12] J. Gibson, P.W. Kållberg, S. Uppala, A. Hernandez, A. Nomura, E. Serrano, “ERA-15 Description,” ECMWF Re-Analysis Project Report Series, 1999.        [ Links ]

[13] ITU-R Recommendation P.1144-9, “Guide to the application of the propagation methods of Radiocommunication Study Group 3,” 2017.        [ Links ]

[14] S. M. Uppala, et al, “The ERA‐40 re‐analysis,” Quarterly Journal of the Royal Meteorological Society, Vol. 131, Nº 162, pp. 2961-3012, 2005.

[15] ITU-R Recommendation P.1510-1, “Mean surface temperature,” 2017.        [ Links ]

[16] L. Luini, L. Emiliani, X. Boulanger, C. Riva, N. Jeannin, “Rainfall Rain Prediction for Propagation Applications: Model Performance at Regional Level over Ireland,” Antennas and Propagation, IEEE Transactions on, Vol. 65, Nº 11, pp. 6185-6189, 2017.

[17] M. Kottek, J. Grieser, C. Beck, B. Rudolf, F. Rubel, “World Map of the Köppen-Geiger climate classification updated,” Meteorologische Zeitschrift, Vol. 15, Nº 3, pp. 259-263, 2006.

[18] URL: https://es.climate-data.org/location/719963/ . Último acceso: 14/05/2018.        [ Links ]

[19] N. Jeannin, et al., “Validation and improvement of precipitation statistical modelling for radiowave propagation,” Antennas and Propagation (EUCAP), 2012 6th European Conference on, 26-30 March. Prague, Czech Republic, 2012.

[20] C. Capsoni, L. Luini, “1-Min Rain Rate Statistics Predictions From 1-Hour Rain Rate Statistics Measurements,” Antennas and Propagation, IEEE Transactions on, Vol. 56, Nº 3, pp. 815-824, 2008.

[21] G. Blarzino, L. Castanet, L. Luini, C. Capsoni, A. Martellucci, “Development of a new global rainfall rate model based on ERA40, TRMM, GPCC and GPCP products,” Antennas and Propagation (EUCAP) 2009, 3rd European Conference on. 23-27 March. Berlin, Germany, 2009.

[22] H. Y. Lam, L. Luini, J. Din, C. Capsoni, A. D. Panagopoulos, “Investigation of Rain Attenuation in Equatorial Kuala Lumpur,” IEEE Antennas and Propagation Letters, Vol. 11, 2012.

[23] N. A. Mohd Aris, L. Luini, J. Din, H.Y. Lam, “1-Minute Integrated Rain Rate Statistics Estimated From Tropical Rainfall Measuring Mission Data,” IEEE Antennas and Propagation Letters, Vol. 12, 2013.

[24] Fascicle Concerning the Rainfall Rate Model Given in Annex 1 to Recommendation ITU-R P.837, document 3J/FAS/3, ITU-R SG3, WP 3J, 2017.