Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Investigación & Desarrollo
versión impresa ISSN 1814-6333versión On-line ISSN 2518-4431
Inv. y Des. vol.2 no.17 Cochabamba 2017
http://dx.doi.org/10.23881/idupbo.017.2-2e
ARTÍCULOS – ECONOMIA Y EMPRESA
ESTIMACIÓN DE LA VOLATILIDAD DE LOS FONDOS DE INVERSIÓN ABIERTOS EN BOLIVIA
VOLATILITY ESTIMATION IN BOLIVIAN OPEN MUTUAL FUNDS
Alejandro Vargas Sanchez
Centro de Investigación e Innovación en Finanzas (CIIFI)
Universidad Privada Boliviana
(Recibido el 05 octubre 2017, aceptado para publicación el 18 de diciembre 2017)
RESUMEN
En el presente documento se desarrollan conceptos y aplicaciones relacionadas con modelos de econometría financiera, el objetivo principal fue la determinación del nivel de volatilidad de los rendimientos reportados por los Fondos de Inversión Abiertos en Bolivia. Mediante la aplicación de los modelos GARCH, MMEP y de Volatilidad Estocástica, se pudo determinar la volatilidad condicional e incondicional. Por otro lado, mediante el uso de los modelos GJR y EGARCH se evaluó la presencia de asimetría en la volatilidad de los rendimientos, finalmente se realizó la estimación del modelo GARCH-M para establecer el nivel de rentabilidad ajustada al riesgo. Los resultados obtenidos mediante el análisis de 28 series de tiempo en un periodo de 5 años, permitieron establecer una línea base para medir el nivel de riesgo existente en la rentabilidad alcanzada por los Fondos de Inversión Abiertos.
Palabras clave: Volatilidad, Fondos de Inversión, GARCH, GJR, EGARCH, GARCH-M, Riesgo.
ABSTRACT
This paper presents the concepts and applications related to financial econometrics models. The main objective was to determine the level of volatility of yields reported by the Open Mutual Funds in Bolivia. By applying the GARCH, EWMA and Stochastic Volatility models, conditional and unconditional volatility could be determined. On the other hand, through the application of the GJR and EGARCH models the presence of asymmetry in the yield volatility was evaluated, finally the estimation of the GARCH-M model was made to establish the level of risk adjusted rate of return. The results obtained through the analysis of 28-time series over a period of 5 years allowed us to establish a base line for measuring the level of risk existing in the profitability achieved by the Open Mutual Funds.
Keywords: Volatility, Mutual Funds, GARCH, GJR, EGARCH, GARCH-M, Risk.
1. INTRODUCCIÓN
La modelización de series de tiempo financieras es un problema complejo que no solo se debe a la variedad de series en uso (acciones, tipos de cambio o tasas de interés), también se debe a la importancia de la frecuencia que tienen las observaciones (segundos, minutos, horas, días, meses, etc.), así como la disponibilidad de grandes conjuntos de datos. Esta complejidad se refleja principalmente en la existencia de regularidades estadísticas (hechos estilizados) que son comunes a un gran número de series financieras, por ejemplo, la existencia de una varianza condicional, es decir, una varianza condicionada al pasado [1].
Desde el trabajo seminal de Engle en 1982 [2] sobre los modelos ARCH, la literatura en econometría ha centrado una atención considerable en: i) comprender cómo la volatilidad varía en el tiempo y ii) en el desarrollo de nuevas herramientas para la medición, la modelización y la predicción de la volatilidad. Estos avances, en gran parte, fueron motivados por la observación empírica de la volatilidad en el rendimiento de los activos financieros, el fenómeno observado se caracteriza por la presencia de una volatilidad condicional que cambia de manera persistente, este fenómeno se presenta a lo largo de diferentes activos, en distintos periodos de tiempo y entre diferentes mercados y países [3].
La volatilidad del retorno de los activos es concepto fundamental en las finanzas, que es utilizado con el propósito de calcular los precios de los activos, la construcción de portafolios de inversión o la gestión de riesgos financieros; por tanto, los métodos y modelos econométricos financieros estándar adquieren una relevancia particular cuando se reconocen estas aplicaciones.
La medición del riesgo en el sistema financiero boliviano y en particular en el mercado de valores, es un tema que aún no ha sido estudiado con la suficiente profundidad, por esta razón, el objetivo del presente trabajo es aplicar modelos de econometría financiera para determinar el nivel de volatilidad en los rendimientos reportados por los Fondos de Inversión en Bolivia.
En ese marco, el trabajo se desarrolla en cuatro partes: luego de la introducción en la segunda parte se presenta una revisión de la literatura sobre los modelos clásicos de estimación de volatilidad como ser el modelo ARCH, el modelo de medias móviles exponenciales ponderadas MMEP y el modelo GARCH, luego se hace una exposición de los modelos de volatilidad asimétrica como GJR y el EGARCH, posteriormente se desarrolla el modelo de volatilidad en media GARCH-M, el modelo de volatilidad estocástica para finalmente exponer un método para realizar las proyecciones de la volatilidad a partir de los parámetros estimados mediante un modelo GARCH. En la tercera parte del trabajo se presentan los resultados de la investigación realizada a partir del estudio de 28 diferentes series de tiempo mensuales para un periodo de 5 años, que permitió obtener la medición de la volatilidad para cada uno de los Fondos de Inversión Abiertos en Bolivia, finalmente en la cuarta parte se presentan las conclusiones del trabajo.
2. MODELOS DE ESTIMACIÓN DE LA VOLATILIDAD
Se define a ![]() como la volatilidad de una variable de mercado durante el periodo n, calculada al final del periodo n-1 [4]. El cuadrado de la volatilidad,
como la volatilidad de una variable de mercado durante el periodo n, calculada al final del periodo n-1 [4]. El cuadrado de la volatilidad, ![]() en el periodo n es la tasa de variación. Si suponemos que el valor de la variable de mercado al final del periodo i es igual a
en el periodo n es la tasa de variación. Si suponemos que el valor de la variable de mercado al final del periodo i es igual a ![]() , la variable
, la variable ![]() se define como el rendimiento compuesto continuo durante el periodo i y se expresa mediante la siguiente relación:
se define como el rendimiento compuesto continuo durante el periodo i y se expresa mediante la siguiente relación:
![]()
Un estimador insesgado de la varianza, ![]() utilizando las m observaciones más recientes sobre
utilizando las m observaciones más recientes sobre ![]() se expresa mediante la siguiente ecuación:
se expresa mediante la siguiente ecuación:
![]()
donde ![]() es la media de
es la media de ![]() y se calcula como:
y se calcula como: ![]()
Con el propósito de monitorear la volatilidad, la fórmula en la ecuación (2) se cambia tomando en cuenta los siguientes aspectos:
● ![]() se define como el porcentaje de cambio en la variable de mercado entre el final del periodo i-1 y el final del periodo i, tal que:
se define como el porcentaje de cambio en la variable de mercado entre el final del periodo i-1 y el final del periodo i, tal que: ![]()
● Se asume que ![]() es igual a cero, debido a que el cambio esperado en la variable en un periodo corto es muy pequeño cuando es comparado con la desviación estándar de los cambios.
es igual a cero, debido a que el cambio esperado en la variable en un periodo corto es muy pequeño cuando es comparado con la desviación estándar de los cambios.
● m-1 se reemplaza por m, pasando de una estimación insesgada de la varianza a una estimación por máxima verosimilitud.
Estos tres cambios permiten simplificar la fórmula de la varianza en la siguiente expresión[1]:
![]()
2.1. Sistema Ponderado y el Modelo ARCH
La ecuación (3) otorga igual ponderación a cada uno de los valores ![]() ,
, ![]() ,
,
,
, ![]() , en cambio, si el objetivo es otorgar mayor ponderación a los datos más recientes se puede aplicar un modelo con la siguiente expresión:
, en cambio, si el objetivo es otorgar mayor ponderación a los datos más recientes se puede aplicar un modelo con la siguiente expresión:
![]()
donde la variable ![]() es la cantidad de peso que se le asigna a la observación i periodos atrás y los coeficientes
es la cantidad de peso que se le asigna a la observación i periodos atrás y los coeficientes ![]() son positivos. Si se seleccionan los valores de alfa tal que
son positivos. Si se seleccionan los valores de alfa tal que ![]() <
<![]() cuando i > j, entonces, menor peso se asignará a las observaciones más antiguas. Las ponderaciones deberán sumar uno, es decir,
cuando i > j, entonces, menor peso se asignará a las observaciones más antiguas. Las ponderaciones deberán sumar uno, es decir, ![]() .
.
Una extensión de la idea formulada en la ecuación (4) es asumir que existe una tasa de varianza promedio de largo plazo y que a ésta se le debería asignar una ponderación [4]. Esto lleva a un modelo que toma la siguiente forma:
![]()
donde ![]() es la tasa de variación de largo plazo
es la tasa de variación de largo plazo ![]() es el peso asignado a
es el peso asignado a ![]() , puesto que los pesos deben sumar 1 se obtiene que:
, puesto que los pesos deben sumar 1 se obtiene que: ![]() .
.
La ecuación (5) es conocida como el modelo Autorregresivo Condicional Heterocedástico ARCH(m), el cual fue inicialmente propuesto por Engle, la idea original fue encontrar un modelo que pudiera evaluar la validez de la conjetura de Friedman sobre el hecho que la imprevisibilidad de la inflación era una causa primaria de los ciclos económicos, la incertidumbre debido a esta imprevisibilidad afectaría el comportamiento de los inversionistas. La búsqueda de esta idea requería un modelo en el que esa incertidumbre pudiera cambiar con el tiempo, Engle aplicó su modelo ARCH que le permitió parametrizar la heterocedasticidad condicional en una ecuación de salarios y precios para el Reino Unido.
En el modelo original Engle estableció ![]() como una variable aleatoria con una media y una varianza condicionadas a un conjunto de información
como una variable aleatoria con una media y una varianza condicionadas a un conjunto de información ![]() (en el campo
(en el campo ![]() generado por
generado por ![]() ,
, ![]() ), éste modelo ARCH de
), éste modelo ARCH de ![]() estaba sujeto a las siguientes propiedades: i) en primer lugar
estaba sujeto a las siguientes propiedades: i) en primer lugar ![]() , ii) la varianza condicional
, ii) la varianza condicional ![]() es una función paramétrica no trivial con valor positivo de
es una función paramétrica no trivial con valor positivo de ![]() .
.
Corresponde destacar que la secuencia ![]() puede ser una secuencia de error o innovación dentro de un modelo econométrico, o puede ser una variable que es observada directamente.
puede ser una secuencia de error o innovación dentro de un modelo econométrico, o puede ser una variable que es observada directamente.
En el primer caso, si se trata de una innovación ![]() se puede expresar mediante la siguiente ecuación:
se puede expresar mediante la siguiente ecuación:
![]()
donde ![]() es una variable aleatoria observable,
es una variable aleatoria observable, ![]() la media condicional[2] de
la media condicional[2] de ![]() dado
dado ![]() . La aplicación de Engle fue de este tipo. Engle asumió que
. La aplicación de Engle fue de este tipo. Engle asumió que ![]() puede descomponerse de la siguiente manera[3]:
puede descomponerse de la siguiente manera[3]:
![]()
donde ![]() es una secuencia de variables aleatorias independientes, idénticamente distribuidas (iid) con media cero y varianza unitaria. Esto implica que
es una secuencia de variables aleatorias independientes, idénticamente distribuidas (iid) con media cero y varianza unitaria. Esto implica que ![]() y donde D representa la distribución (generalmente se supone que es una Distribución Normal o una Leptocúrtica). La siguiente expresión define la varianza condicional mediante un modelo ARCH de orden m:
y donde D representa la distribución (generalmente se supone que es una Distribución Normal o una Leptocúrtica). La siguiente expresión define la varianza condicional mediante un modelo ARCH de orden m:
![]()
donde, ![]() , estas restricciones en los parámetros de la ecuación (8) forman una condición necesaria y suficiente para que la varianza condicional sea positiva, por otro lado, si la varianza incondicional viene dada por
, estas restricciones en los parámetros de la ecuación (8) forman una condición necesaria y suficiente para que la varianza condicional sea positiva, por otro lado, si la varianza incondicional viene dada por ![]() , por tanto, la definición de
, por tanto, la definición de ![]() a través de la descomposición de la ecuación (7) que implica a
a través de la descomposición de la ecuación (7) que implica a ![]() , garantiza la propiedad de ruido blanco de la secuencia
, garantiza la propiedad de ruido blanco de la secuencia ![]() , puesto que
, puesto que ![]() es una secuencia de variables iid [5].
es una secuencia de variables iid [5].
En el segundo caso, si la secuencia de variables se puede observar directamente, la estimación de la varianza se basa en la variación media a largo plazo a lo largo de m observaciones. Cuanta más antigua sea una observación, menos peso se le dará. Definiendo ![]() , el modelo en la ecuación (5) puede escribirse como:
, el modelo en la ecuación (5) puede escribirse como:
![]()
Aunque la aplicación original de Engle no fue financiera, pronto muchos autores se dieron cuenta del potencial del modelo ARCH en aplicaciones financieras que requerían realizar pronósticos de la volatilidad.
El modelo ARCH y sus generalizaciones se aplican, por lo tanto, al modelado, entre otras cosas, de las tasas de interés, los tipos de cambio y los rendimientos de las acciones y los índices bursátiles. Bollerslev [6] ya enumeró una variedad de aplicaciones, resaltando que la predicción de la volatilidad de estas series es diferente de la predicción de la media condicional de un proceso debido a que la volatilidad, el objeto a prever, debe ser observado, puede ser estimada mediante el error o como se expone en este documento a través de la medición de la tasa de variación de las series de tiempo.
2.2. El modelo de medias móviles ponderadas exponenciales
El modelo de medias móviles ponderadas exponenciales es un caso particular del modelo expresado en la ecuación (4) en el cual las ponderaciones ![]() decrecen en forma exponencial a medida que se retrocede en el tiempo. Específicamente
decrecen en forma exponencial a medida que se retrocede en el tiempo. Específicamente ![]() , donde
, donde ![]() es una constante que se encuentra entre 0 y 1 [4].
es una constante que se encuentra entre 0 y 1 [4].
Resulta que este esquema de ponderación conduce a una fórmula especialmente simple para actualizar las estimaciones de volatilidad, expresada en la siguiente ecuación:
![]()
La estimación ![]() , de la volatilidad para el periodo n correspondiente a la variable (realizada al final del periodo n-1) se calcula a partir de
, de la volatilidad para el periodo n correspondiente a la variable (realizada al final del periodo n-1) se calcula a partir de ![]() y de
y de ![]() (el más reciente cambio porcentual de la variable)[4].
(el más reciente cambio porcentual de la variable)[4].
El modelo de medias móviles ponderadas exponenciales (MMPE) tiene la característica atractiva que necesita obtener pocos datos para realizar las proyecciones. En cualquier momento, solamente la última estimación de la tasa de variación y la más reciente observación de la variable de mercado es requerida, a partir de esta información se puede calcular un nuevo cambio porcentual, luego la ecuación (10) es utilizada para actualizar la estimación de la siguiente tasa de variación. Finalmente, la antigua estimación de la tasa de variación y el valor antiguo de la variable de mercado pueden ser descartados.
El enfoque de MMPE está diseñado para realizar un seguimiento de los cambios en la volatilidad, supongamos que hay un gran movimiento en la variable de mercado en el día n-1, por lo que ![]() tiene un valor alto, de la ecuación (10) esto hace que la estimación de la volatilidad actual se mueva hacia arriba, el valor de
tiene un valor alto, de la ecuación (10) esto hace que la estimación de la volatilidad actual se mueva hacia arriba, el valor de ![]() gobierna la sensibilidad de la estimación de la volatilidad diaria frente a los cambios más recientes, por ejemplo: i) un valor bajo de
gobierna la sensibilidad de la estimación de la volatilidad diaria frente a los cambios más recientes, por ejemplo: i) un valor bajo de ![]() conduce a un mayor peso dado a
conduce a un mayor peso dado a ![]() cuando
cuando ![]() es calculada, en este caso, las estimaciones producidas por la volatilidad en los días sucesivos son en sí mismas muy volátiles, ii) un valor alto de
es calculada, en este caso, las estimaciones producidas por la volatilidad en los días sucesivos son en sí mismas muy volátiles, ii) un valor alto de ![]() produce estimaciones de la volatilidad diaria que responden con relativa lentitud a la nueva información proporcionada por el cambio porcentual diario.
produce estimaciones de la volatilidad diaria que responden con relativa lentitud a la nueva información proporcionada por el cambio porcentual diario.
2.3. El modelo GARCH
En las aplicaciones financieras, el modelo ARCH ha sido reemplazado por el denominado modelo ARCH generalizado conocido como modelo GARCH[5] que Bollerslev [6] y Taylor [7] propusieron independientemente entre sí.
La diferencia del modelo GARCH (1,1) respecto al modelo MMEP es análoga a la diferencia que existe entre la ecuación (4) y (5). En el modelo GARCH (1,1) ![]() se calcula a partir de una tasa de varianza media a largo plazo,
se calcula a partir de una tasa de varianza media a largo plazo,![]() , así como de
, así como de ![]() y
y ![]() . La ecuación para GARCH (1,1) es la siguiente [4]:
. La ecuación para GARCH (1,1) es la siguiente [4]:
![]()
donde ![]() es el peso asignado a
es el peso asignado a ![]() ,
, ![]() es el peso asignado a
es el peso asignado a ![]() , y
, y ![]() es el peso asignado a
es el peso asignado a ![]() . Dado que los pesos deben sumar a la unidad, se deduce que:
. Dado que los pesos deben sumar a la unidad, se deduce que: ![]() .
.
El modelo MMPE es un caso particular de GARCH (1,1) donde, ![]()
Ajustando ![]() , el modelo GARCH (1,1) también se puede escribir mediante la siguiente ecuación:
, el modelo GARCH (1,1) también se puede escribir mediante la siguiente ecuación:
![]()
Esta es la forma del modelo que generalmente se utiliza para estimar los parámetros. Una vez que ![]() se han estimado, se puede calcular
se han estimado, se puede calcular ![]() . La tasa de variación a largo plazo será igual a
. La tasa de variación a largo plazo será igual a ![]() .
.
Para un proceso estable de GARCH (1,1) se necesita que a + b < 1, en caso contrario el peso asignado a la varianza de largo plazo será negativa.
Una condición suficiente para que la varianza condicional sea positiva es ![]() . Las condiciones necesarias y suficientes para la positividad de la varianza condicional en los modelos GARCH de orden superior son más complicadas que las condiciones suficientes que acabamos de mencionar [8].
. Las condiciones necesarias y suficientes para la positividad de la varianza condicional en los modelos GARCH de orden superior son más complicadas que las condiciones suficientes que acabamos de mencionar [8].
2.4. Extensiones al modelo GARCH univariado
Desde su introducción, el modelo GARCH ha sido generalizado y ampliado en varias direcciones, con el objetivo de aumentar la flexibilidad del modelo original. Por ejemplo, la especificación GARCH original asume que la respuesta de la varianza a un choque es independiente del signo del choque y sólo es una función del tamaño del choque. Varias extensiones del modelo GARCH apuntan a acomodar la asimetría en la respuesta.
2.4.1. Modelos de Volatilidad asimétrica
Una de las principales restricciones de los modelos GARCH es que imponen una respuesta simétrica de la volatilidad a los choques positivos y negativos. Esto se debe a que la varianza condicional en ecuaciones tales como (12) es una función de las magnitudes de los residuos rezagados y no de sus signos (es decir, al cuadrar el error retrasado en (12), el signo se pierde). Sin embargo, se ha argumentado que un choque negativo a series de tiempo financieras es probable que cause que la volatilidad suba en mayor proporción que un choque positivo de la misma magnitud. En el caso de rendimientos de capital, tales asimetrías se atribuyen típicamente a efectos de apalancamiento, por lo que una caída en el valor de las acciones de una empresa hace que el ratio deuda/patrimonio de la empresa aumente. Esto lleva a los accionistas, que asumen el riesgo residual de la empresa, a percibir su flujo de caja futuro como relativamente más riesgoso [9].
Una visión alternativa es proporcionada por la hipótesis de la "retroalimentación en la volatilidad", suponiendo dividendos constantes, si los retornos esperados aumentan cuando aumenta la volatilidad de los precios de las acciones, los precios de las acciones deberían caer cuando la volatilidad aumente. Aunque las asimetrías en series de rentabilidades distintas de las acciones no pueden atribuirse al cambio de apalancamiento, tampoco hay razón para suponer que tales asimetrías sólo existen en las rentabilidades de las acciones [9].
● El modelo GJR-GARCH
El modelo GJR-GARCH propuesto por Glosten, Jagannathan y Runkle [10], es una simple extensión de GARCH con un término adicional añadido para dar cuenta de posibles asimetrías. La variación condicional viene dada por la ecuación (13),
![]()
donde ![]() si
si ![]() , 0 en otro caso.
, 0 en otro caso.
Frente a la presencia del efecto de apalancamiento, se vería que γ> 0. Se observa ahora que la condición para la no negatividad será ![]() > 0,
> 0, ![]() > 0, β ≥ 0, y
> 0, β ≥ 0, y ![]() + γ ≥ 0. Es decir, el modelo sigue siendo admisible, incluso si γ <0, siempre que
+ γ ≥ 0. Es decir, el modelo sigue siendo admisible, incluso si γ <0, siempre que ![]() + γ ≥ 0.
+ γ ≥ 0.
● El modelo EGARCH
El modelo Exponencial GARCH fue propuesto por Nelson [11]. Hay varias maneras de expresar la ecuación de la varianza condicional, pero una posible especificación planteada por Brooks (2008) viene dada por:
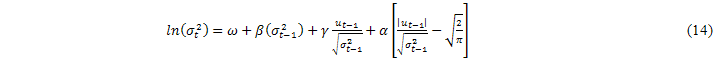
El modelo tiene varias ventajas sobre la especificación GARCH pura. En primer lugar, puesto que el log (![]() ) es modelado, entonces, incluso si los parámetros son negativos,
) es modelado, entonces, incluso si los parámetros son negativos, ![]() será positivo. Por lo tanto, no es necesario imponer artificialmente restricciones de no negatividad a los parámetros del modelo. En segundo lugar, las asimetrías se permiten bajo la formulación de EGARCH, ya que, si la relación entre la volatilidad y los rendimientos es negativa, γ será negativa.
será positivo. Por lo tanto, no es necesario imponer artificialmente restricciones de no negatividad a los parámetros del modelo. En segundo lugar, las asimetrías se permiten bajo la formulación de EGARCH, ya que, si la relación entre la volatilidad y los rendimientos es negativa, γ será negativa.
2.4.2. El modelo de volatilidad en media, GARCH-M
La mayoría de los modelos utilizados en las finanzas suponen que los inversores deben ser recompensados por asumir riesgos adicionales al obtener un mayor rendimiento. Una forma de operacionalizar este concepto es permitir que el retorno de un valor esté determinado en parte por su riesgo. Engle, Lilien y Robins [12] sugirieron una especificación ARCH-M, donde la varianza condicional de los rendimientos de los activos se incorpora en la ecuación de la media condicional. Dado que los modelos GARCH son ahora mucho más populares que ARCH, es más común estimar un modelo GARCH-M. Un ejemplo de un modelo GARCH-M viene dado por la siguiente especificación:
![]()
Si δ es positivo y estadísticamente significativo, entonces el riesgo aumentado, que viene dado por un aumento en la varianza condicional, conduce a un aumento en el retorno medio. Así, δ puede interpretarse como una prima de riesgo. En algunas aplicaciones empíricas, el término de la varianza condicional, ![]() , aparece directamente en la ecuación condicional media, en lugar de la raíz cuadrada. Además, en algunas aplicaciones el término puede ser contemporáneo,
, aparece directamente en la ecuación condicional media, en lugar de la raíz cuadrada. Además, en algunas aplicaciones el término puede ser contemporáneo, ![]() en lugar de estar rezagado.
en lugar de estar rezagado.
2.4.3. El modelo de volatilidad estocástica
El modelo GARCH (1,1) reconoce que con el tiempo la varianza tiende a recuperarse a un nivel medio de largo plazo de ![]() . La cantidad de peso asignada a
. La cantidad de peso asignada a ![]() viene dada por un coeficiente a. El GARCH (1,1) es equivalente a un modelo donde la varianza V sigue el siguiente proceso estocástico [4]:
viene dada por un coeficiente a. El GARCH (1,1) es equivalente a un modelo donde la varianza V sigue el siguiente proceso estocástico [4]:
![]()
donde el tiempo se puede medir en días o meses, ![]() , y
, y ![]() . Este es un modelo de reversión a la media. La varianza tiene una tendencia que la tira de nuevo a
. Este es un modelo de reversión a la media. La varianza tiene una tendencia que la tira de nuevo a ![]() a una velocidad
a una velocidad ![]() . Cuando V >
. Cuando V > ![]() , la varianza tiene una tendencia negativa; cuando V <
, la varianza tiene una tendencia negativa; cuando V < ![]() , tiene una tendencia positiva. Superpuesto a la tendencia existe una volatilidad
, tiene una tendencia positiva. Superpuesto a la tendencia existe una volatilidad ![]() .
.
2.5. Pronósticos de la volatilidad futura
La tasa de varianza estimada al final del periodo n-1 para el periodo n, cuando se utiliza el modelo GARCH (1,1), es igual a:
![]()
Reagrupando ![]() , se tiene:
, se tiene:
![]()
Para el periodo n + t en el futuro:
![]()
Considerando que el valor esperado de ![]() es igual a
es igual a ![]() , se obtiene la siguiente expresión:
, se obtiene la siguiente expresión:
![]()
donde E, denota valor esperado [4], usando esta ecuación repetidamente produce una estimación de la volatilidad para un periodo t:
![]()
La ecuación (21) pronostica la volatilidad para el periodo n + t utilizando la información disponible al final del periodo n-1.
Como se explicó, en el modelo MMEP los coeficientes ![]() , y la ecuación (10) muestra que la tasa de varianza futura esperada es igual a la tasa de varianza actual. Cuando
, y la ecuación (10) muestra que la tasa de varianza futura esperada es igual a la tasa de varianza actual. Cuando ![]() el término final en la ecuación se hace más pequeño a medida que aumenta t. Como se mencionó anteriormente, la tasa de varianza presenta un proceso de reversión media con un nivel de reversión igual a
el término final en la ecuación se hace más pequeño a medida que aumenta t. Como se mencionó anteriormente, la tasa de varianza presenta un proceso de reversión media con un nivel de reversión igual a ![]() y una tasa de reversión de
y una tasa de reversión de ![]() .
.
3. APLICACIÓN
Existen investigaciones empíricas orientadas a la medición del riesgo, por ejemplo, French, Scwart y Stanbaugh [14] realizaron una estimación de la volatilidad en el retorno de las acciones para el índice SP 500, la muestra presentó una desviación estándar mensual que se encuentra en el rango de 4.1% a 7.42%, William Schwert [15] también realizó un estudio sobre el índice de acciones negociadas en la Bolsa de Nueva York, cuya volatilidad mensual fue de aproximadamente 4%.
El objetivo de este acápite es realizar una aplicación que permita la medición del nivel de volatilidad (riesgo) en la rentabilidad reportada por los Fondos de Inversión Abiertos[6] en Bolivia que se encuentran expresados en bolivianos y expresados en dólares americanos. Se espera que estos resultados sirvan de línea base para evaluar el comportamiento de estos portafolios de inversión.
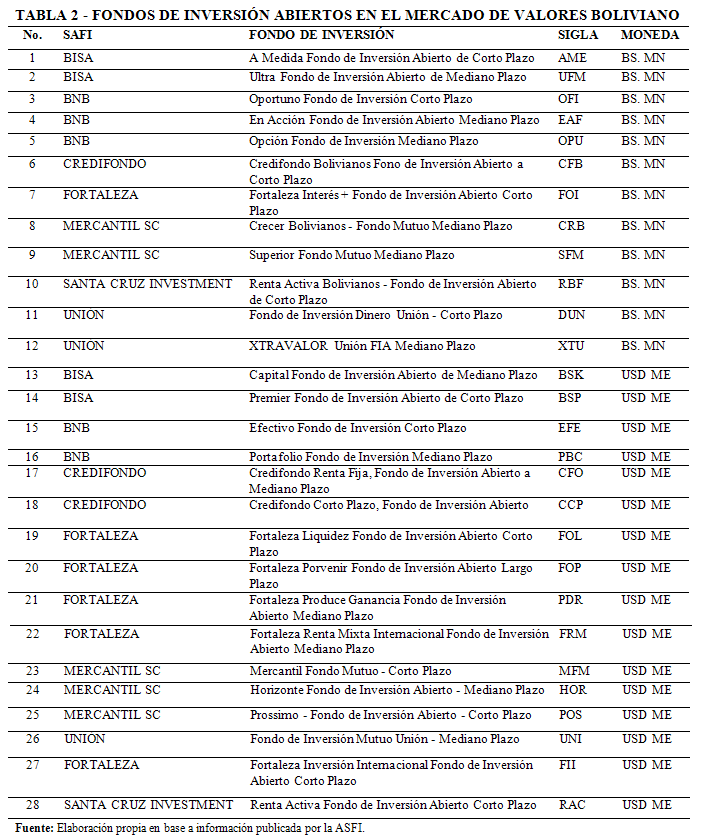
De acuerdo a datos publicados por la Autoridad de Supervisión del Sistema Financiero ASFI, existen un total de 36 Fondos de Inversión Abiertos de los cuales el 47% se encuentran en moneda nacional y el 53% en moneda extranjera, la ASFI reporta la siguiente información diaria de los Fondos:

Para realizar un análisis sobre el desempeño de un portafolio el GIPS[7] recomienda trabajar como mínimo con un periodo de 5 años, los rendimientos del mercado pueden medirse en forma diaria, semanal, mensual, trimestral o anual, sin embargo, como señala Pratt y Grabowski [13] la frecuencia mensual es la más común, por lo que en el presente estudio se trabajó con la rentabilidad a 30 días. En ese sentido, del total de Fondos Abiertos, se obtuvo una muestra de 28 Fondos que cumplen con estos requisitos, de acuerdo a la Tabla 2.
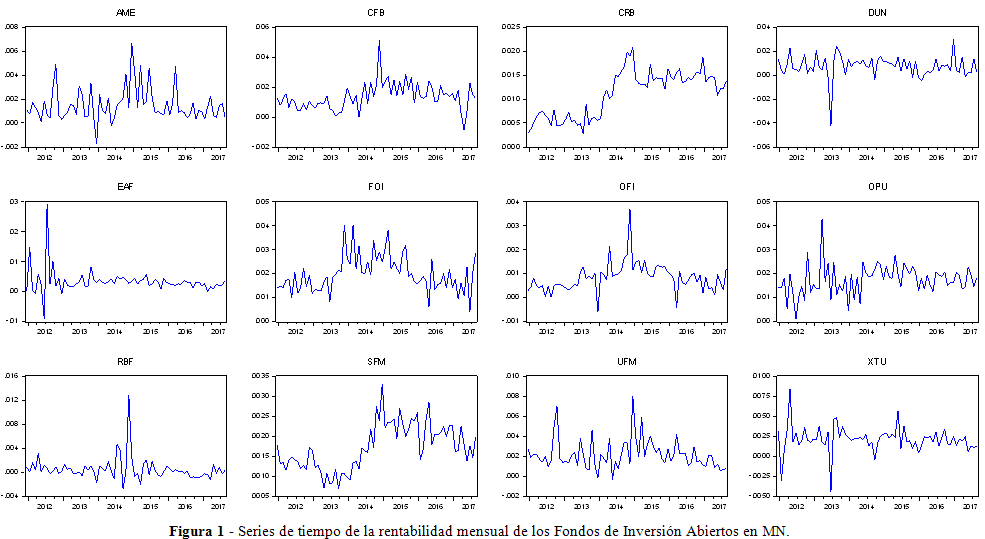
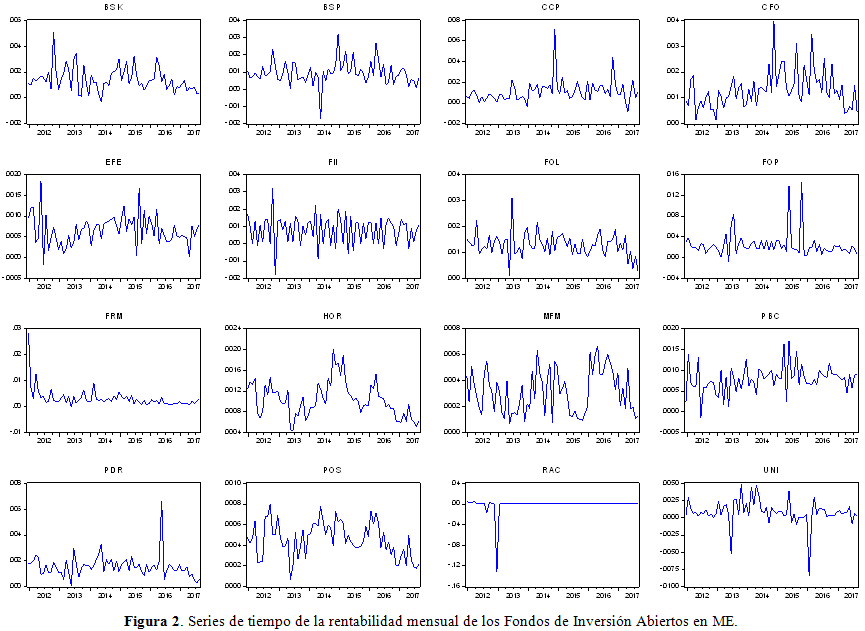
En las Figuras 1 y 2 se presenta la rentabilidad mensual de cada uno de los Fondos desde enero de 2012 hasta julio de 2017[8].
3.1. Estimación del modelo GARCH mediante el método de máxima verosimilitud
El propósito fue estimar la varianza de una variable X a partir de m observaciones sobre X subyacente a una distribución Normal con media igual a cero. Asumiendo que las observaciones son u1, u2,
un, se denota la varianza con ![]() . La verosimilitud de
. La verosimilitud de ![]() de ser observada se define por la función de densidad de probabilidad para X cuando X=
de ser observada se define por la función de densidad de probabilidad para X cuando X= ![]() [9]:
[9]:
![]()
La verosimilitud de m observaciones que ocurren en el orden que fueron observadas viene dada por la siguiente expresión [9]:
![]()
Utilizando el método de máxima verosimilitud, la mejor estimación de ![]() es el valor que maximiza la expresión (24).
es el valor que maximiza la expresión (24).
Maximizar una expresión es equivalente a maximizar el logaritmo de la expresión, tomando logaritmos de la expresión en la ecuación (24) e ignorando los factores multiplicativos constantes, se busca maximizar la siguiente función [9]:
![]()
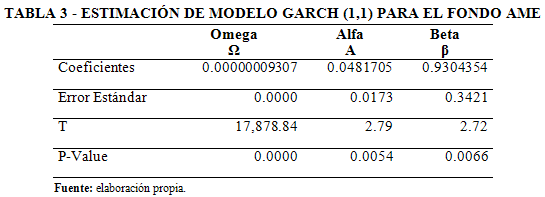
A partir de la ecuación (12) se estimó un modelo GARCH (1,1) con el cual se buscó maximizar el resultado de la expresión (25), en la Tabla 3 se presentan los cálculos realizados para el Fondo de Inversión AME. La estimación de los parámetros Omega, Alfa y Beta, que permitió maximizar la función de verosimilitud fueron calculados mediante la aplicación solver de la hoja de cálculo Excel.
Se evidencia que todos parámetros estimados son estadísticamente significativos al 0.01, el valor máximo alcanzado en la función de verosimilitud fue de 752.34. A partir de estos resultados la varianza de largo plazo para el Fondo AME se calcula como:
![]()
La volatilidad mensual de largo plazo es igual a ![]() y la volatilidad anual de largo plazo[9] es igual a
y la volatilidad anual de largo plazo[9] es igual a ![]() .
.
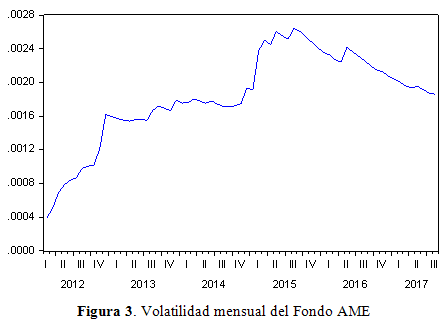
En la Figura 3 se presenta la estimación de la volatilidad de los rendimientos mensuales de la serie sobre los datos históricos, se puede evidenciar la presencia de clusters de volatilidad[10], con volatilidades más altas a lo largo del primer semestre del año 2015.
Para evaluar si el modelo GARCH (1,1) se encuentra correctamente especificado se calcularon las funciones de autocorrelación tanto de ![]() como de la relación
como de la relación ![]() /
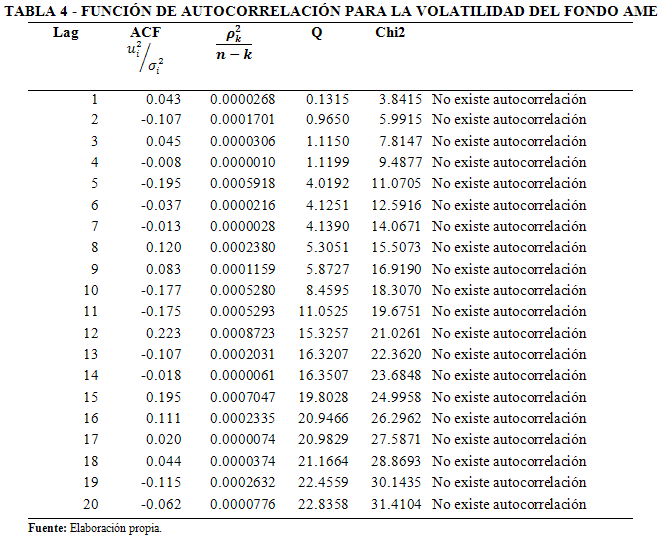
/ ![]() . Asimismo, se calculó el estadístico de Ljung-Box[1] para realizar una prueba de significación estadística en la autocorrelación[12], los resultados expuestos en la Tabla 4 señalan que el modelo se encuentra correctamente especificado, toda vez que no se evidencia autocorrelación en las estimaciones.
. Asimismo, se calculó el estadístico de Ljung-Box[1] para realizar una prueba de significación estadística en la autocorrelación[12], los resultados expuestos en la Tabla 4 señalan que el modelo se encuentra correctamente especificado, toda vez que no se evidencia autocorrelación en las estimaciones.
Para la estimación del modelo de MMPE se establecieron las siguientes restricciones en la optimización ![]() ,
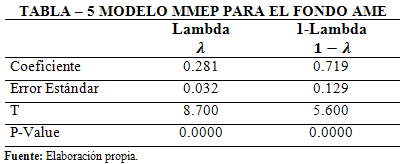
, ![]() , para el caso del Fondo de Inversión AME los resultados se exponen en la Tabla 5.
, para el caso del Fondo de Inversión AME los resultados se exponen en la Tabla 5.
Se observa que todos los coeficientes son estadísticamente significativos al 0.01, a partir de estos resultados tomando en cuenta las últimas observaciones de la muestra en las cuales ![]() y
y ![]() , la proyección de la varianza y la volatilidad para el siguiente mes será igual a:
, la proyección de la varianza y la volatilidad para el siguiente mes será igual a:
![]()
![]()
Este mismo procedimiento fue aplicado para cada uno de los rendimientos obtenidos en los 28 Fondos de Inversión[13], los resultados alcanzados reflejan que 12 modelos no presentan problemas de autocorrelación en las estimaciones, adicionalmente la totalidad de estos modelos tienen coeficientes que son estadísticamente significativos al 0.10, la estimación de la volatilidad mensual de largo plazo (volatilidad incondicional), se encuentra en el rango de 0.05% a 1.26%, en el caso de la volatilidad anual ésta se encuentra en el rango de 0.17% a 5.63%, situación que refleja que en general existe un bajo nivel de riesgo en la rentabilidad de los Fondos de Inversión[14].
En todos los casos se pudo realizar la estimación de los parámetros correspondientes al Modelo de Medias Móviles Exponenciales Ponderadas MMEP, se puede apreciar que 17 Fondos tienen un coeficiente ![]() menor a 0.35, lo que implica que la estimación de la varianza se ve afectada en mayor proporción por los cambios recientes en la rentabilidad, por otro lado, los pronósticos de volatilidad para el siguiente mes a partir de éste modelo se encuentran en el rango de 0.02% a 0.30% resultados que en general se encuentran por debajo de sus valores de largo plazo.
menor a 0.35, lo que implica que la estimación de la varianza se ve afectada en mayor proporción por los cambios recientes en la rentabilidad, por otro lado, los pronósticos de volatilidad para el siguiente mes a partir de éste modelo se encuentran en el rango de 0.02% a 0.30% resultados que en general se encuentran por debajo de sus valores de largo plazo.
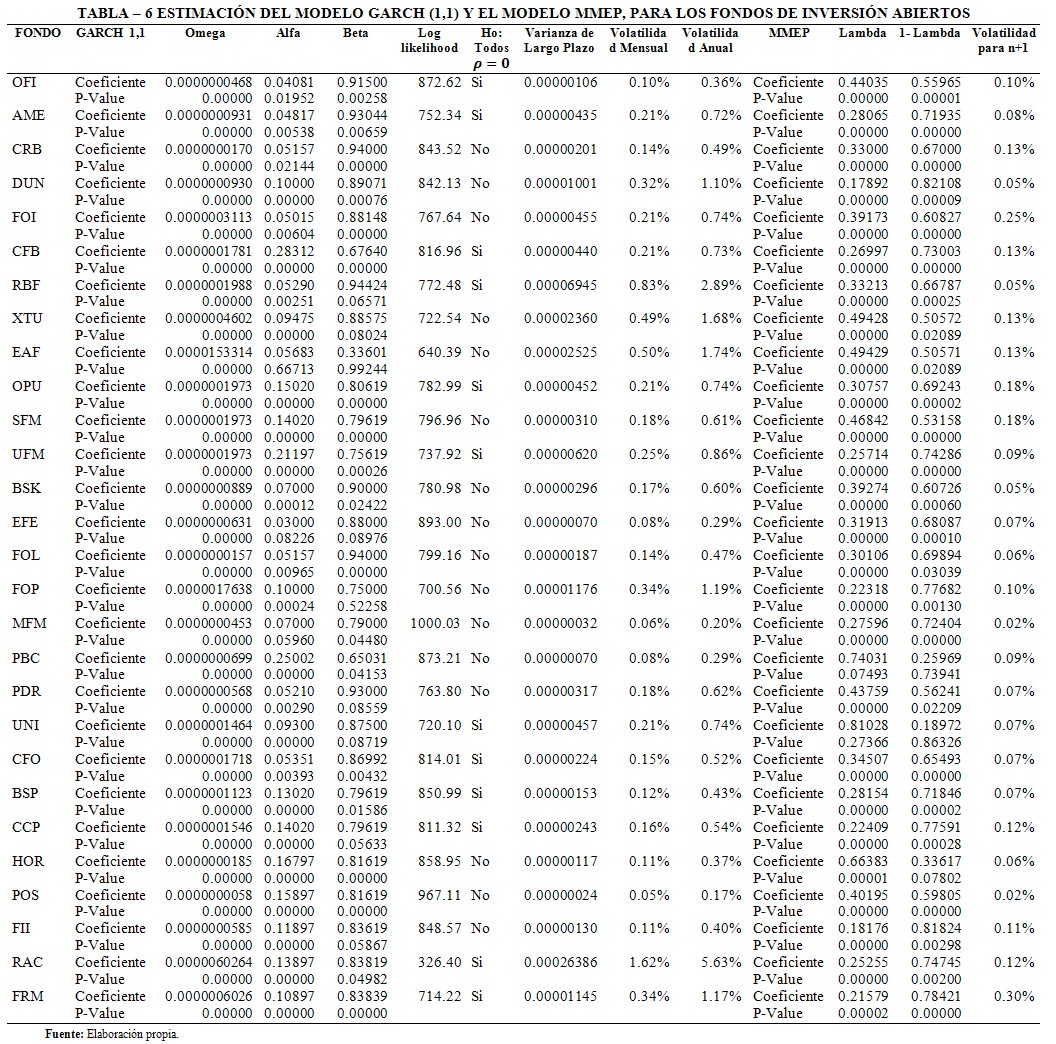
En la Tabla 6 se presenta el resumen de los resultados alcanzados[15].
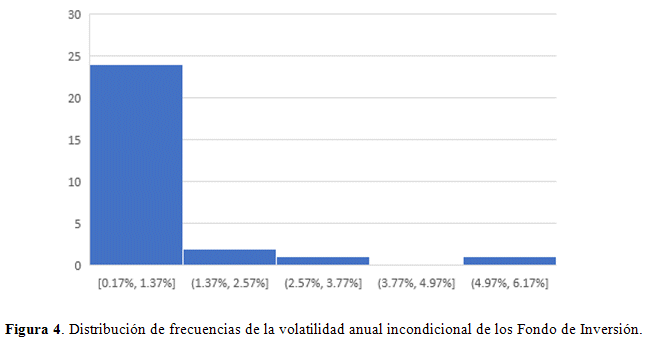
Los datos obtenidos mediante el modelo GARCH (1,1) muestran que 21 Fondos reportaron un nivel de volatilidad incondicional anual menor al 0.90%, 5 Fondos tienen un nivel de volatilidad anual que se encuentra entre 1.10% y 1.74%, finalmente 2 Fondos presentan los niveles de volatilidad más altos con 2.89% y 5.63%. En la siguiente Figura 4 se presenta una distribución de frecuencias de la volatilidad anual.
3.2. Proyección de la Volatilidad
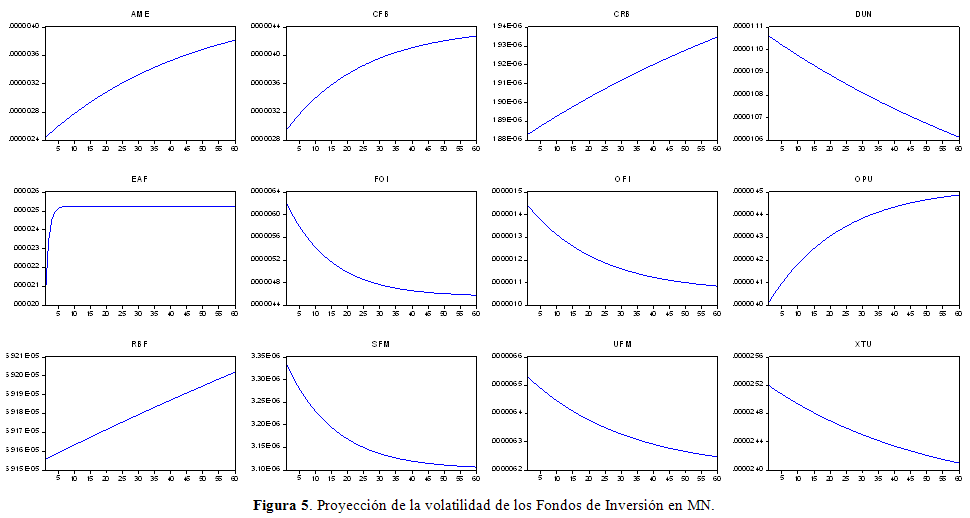
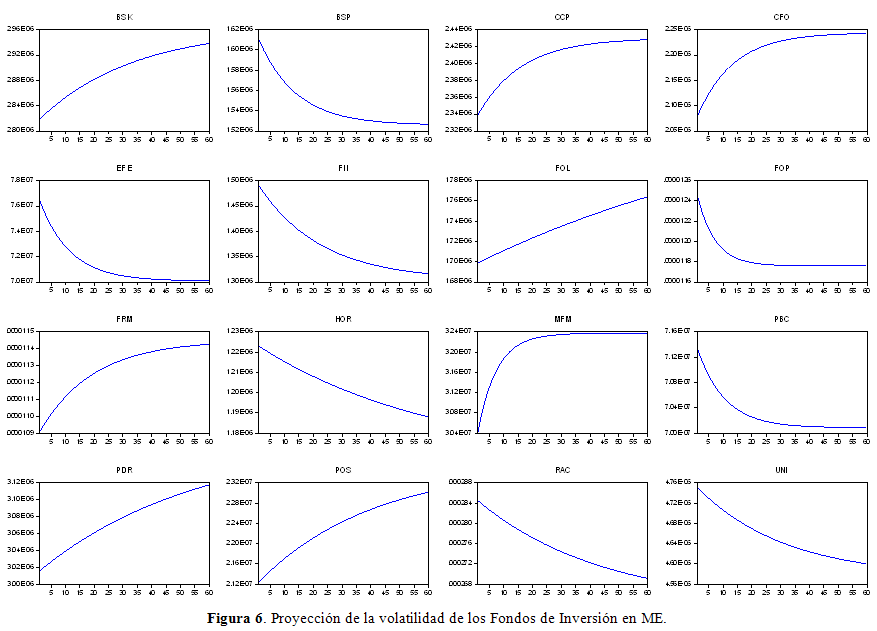
Se realizó una proyección de la volatilidad mediante la aplicación de la ecuación (21), en las siguientes Figuras 5 y 6, se presenta el proceso de convergencia a lo largo de un periodo de 60 meses (5 años) en el nivel de volatilidad de los Fondos de Inversión.
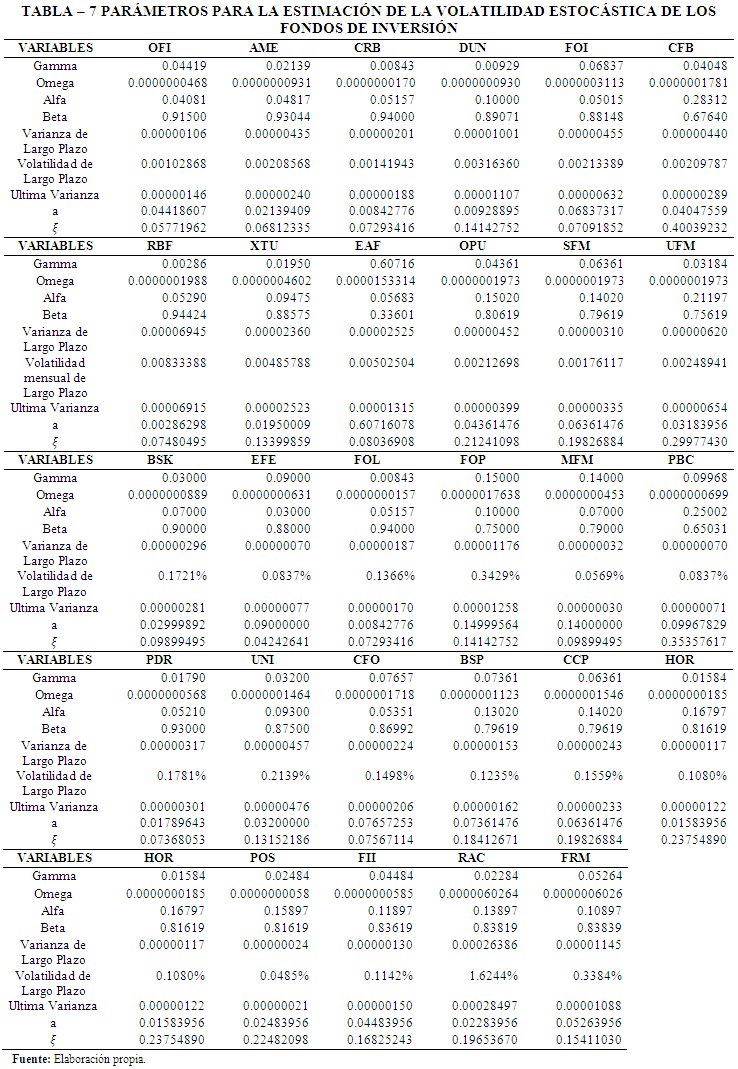
A partir de los resultados obtenidos mediante el modelo GARCH (1,1) fue posible estimar los parámetros necesarios para la aplicación del modelo de volatilidad estocástica mediante la aplicación de la ecuación (17), en la Tabla 7 se presentan las estimaciones realizadas para cada uno de los Fondos de Inversión:
En base a estos parámetros se implementó un proceso de simulación Monte Carlo mediante la aplicación de 10.000 escenarios, para realizar la proyección de la volatilidad para un periodo (n+1) el siguiente mes
Las estimaciones de la volatilidad para el siguiente periodo se encuentran en el rango de 0.046% a 1.678%, adicionalmente, los resultados reflejan que más del 50% de los Fondos de Inversión el promedio de la simulación converge a su nivel de largo plazo, el restante, requerirán más periodos para alcanzar su nivel de reversión a la media.
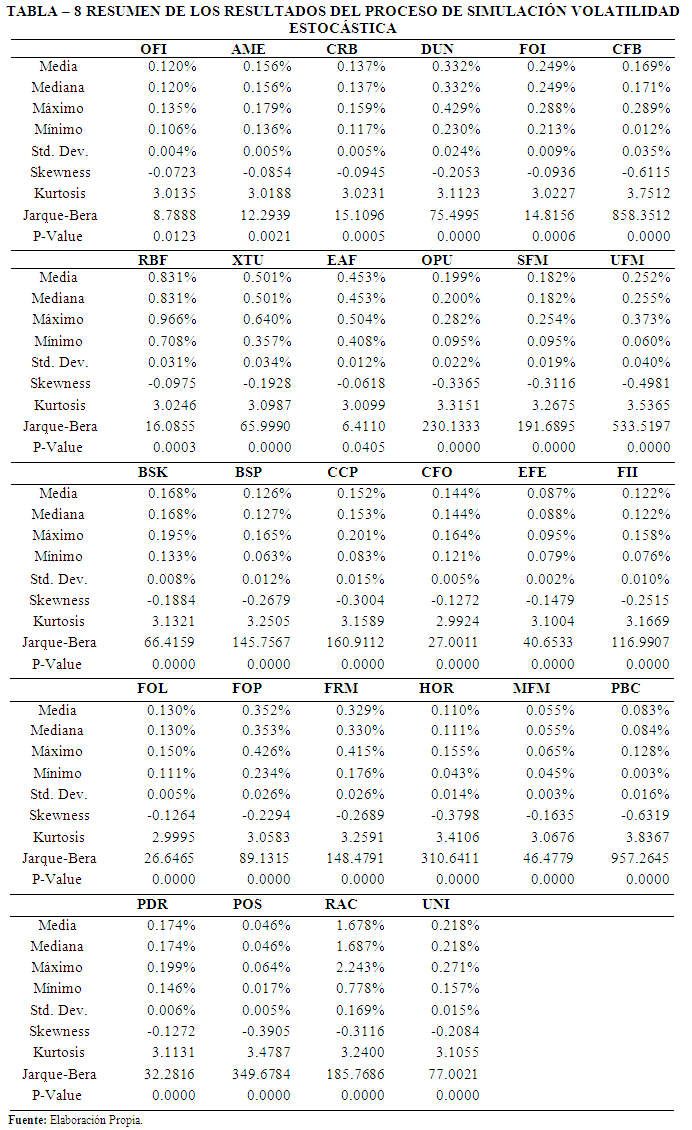
Por otro lado, los resultados alcanzados mediante el modelo de volatilidad estocástica, permiten evidenciar que la volatilidad esperada tiene una desviación en sus resultados (volatilidad de la volatilidad) la cual se encuentra en el rango de 0.002% a 0.169%. En la Tabla 8 se presenta el resumen de los resultados alcanzados.
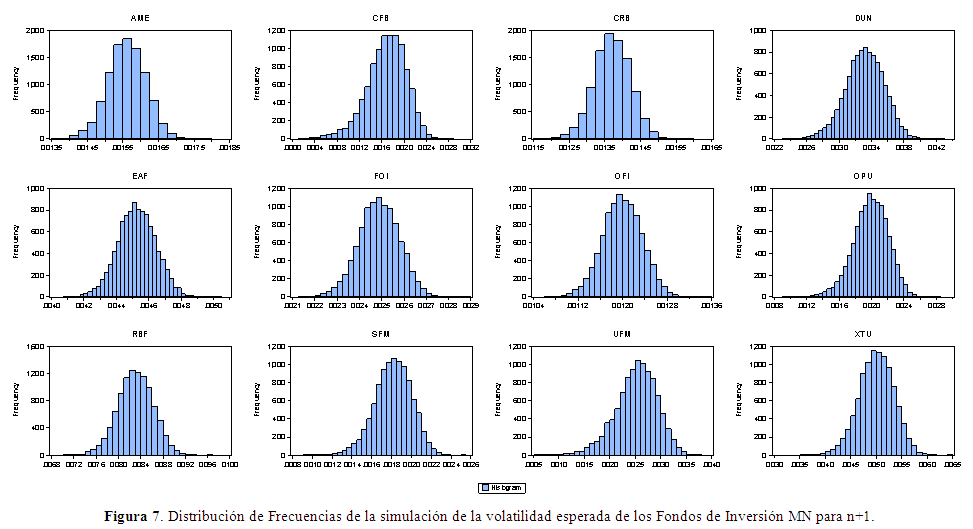
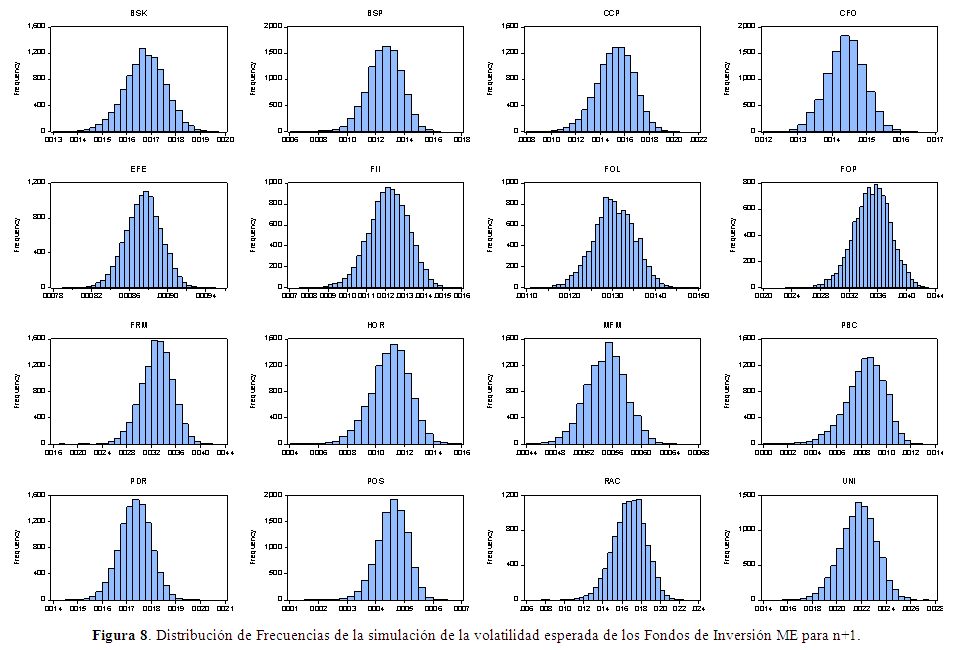
En las Figuras 7 y 8 se presenta la distribución de frecuencia del proceso de simulación.
3.3. Evaluación de la presencia de volatilidad asimétrica
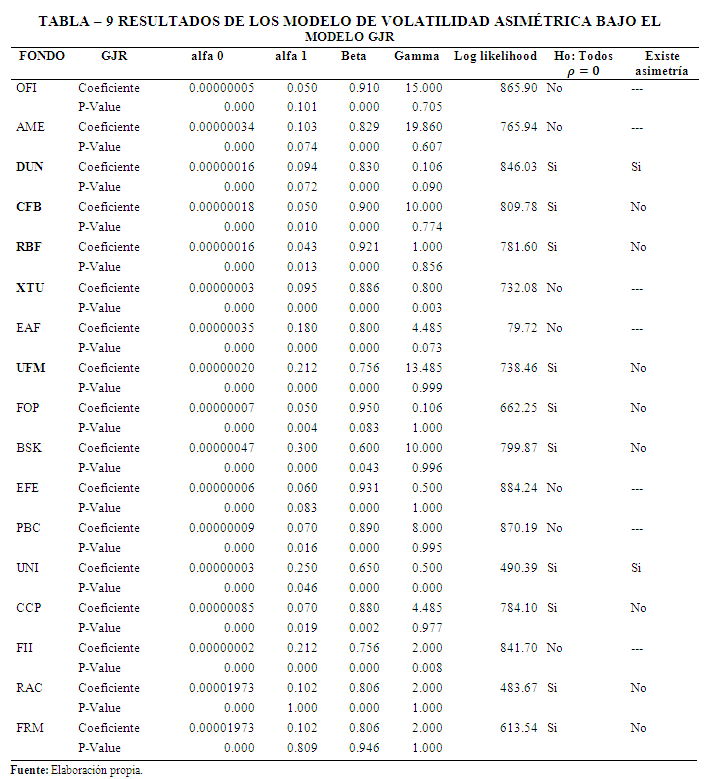
Se analizó la presencia de asimetría en el comportamiento de los retornos alcanzados por los Fondos de Inversión, para todos aquellos Fondos de Inversión que en el periodo de estudio obtuvieron retornos negativos. Se realizó la prueba de volatilidad asimétrica mediante la aplicación del modelo GJR y el modelo EGARCH expuestos en las ecuaciones (13) y (14) respectivamente.
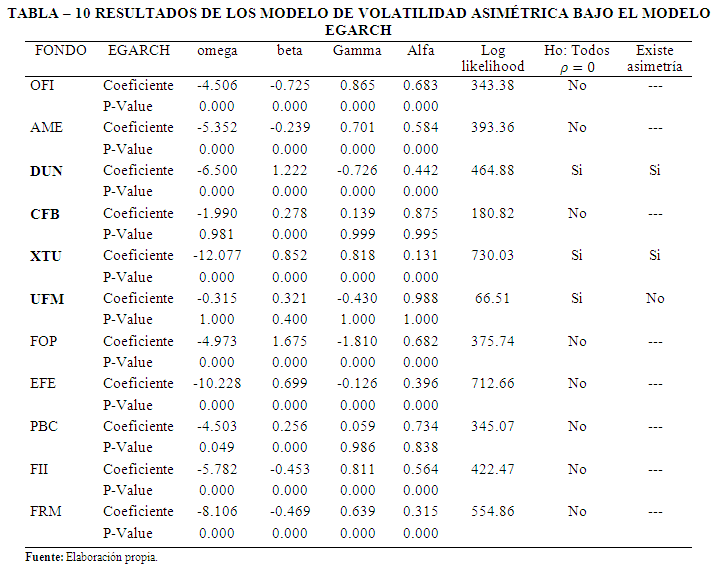
Los resultados obtenidos muestran que 3 Fondos de Inversión presentaron una respuesta asimétrica en la volatilidad, no se incluyeron los Fondos CRB, FOI, OPU, SFM, POS, HOR, BSP, CFO, PDR, KFM y FOL, debido a que no reportaron rendimientos negativos en el periodo de análisis. En el resto de los Fondos no se pudo detectar la presencia de este fenómeno debido a que los modelos presentaron problemas de autocorrelación, por otro lado, corresponde destacar el caso particular del Fondo XTU, en el cual la respuesta asimétrica se presenta cuando el shock es positivo, contrariamente al resultado esperado, esta situación se pudo identificar debido a que el signo esperado en el coeficiente gamma es negativo, sin embargo, para este Fondo el signo fue positivo. Todos estos resultados se presentan en las Tablas 9 y 10.
3.4. Estimación de la rentabilidad ajustada al riesgo
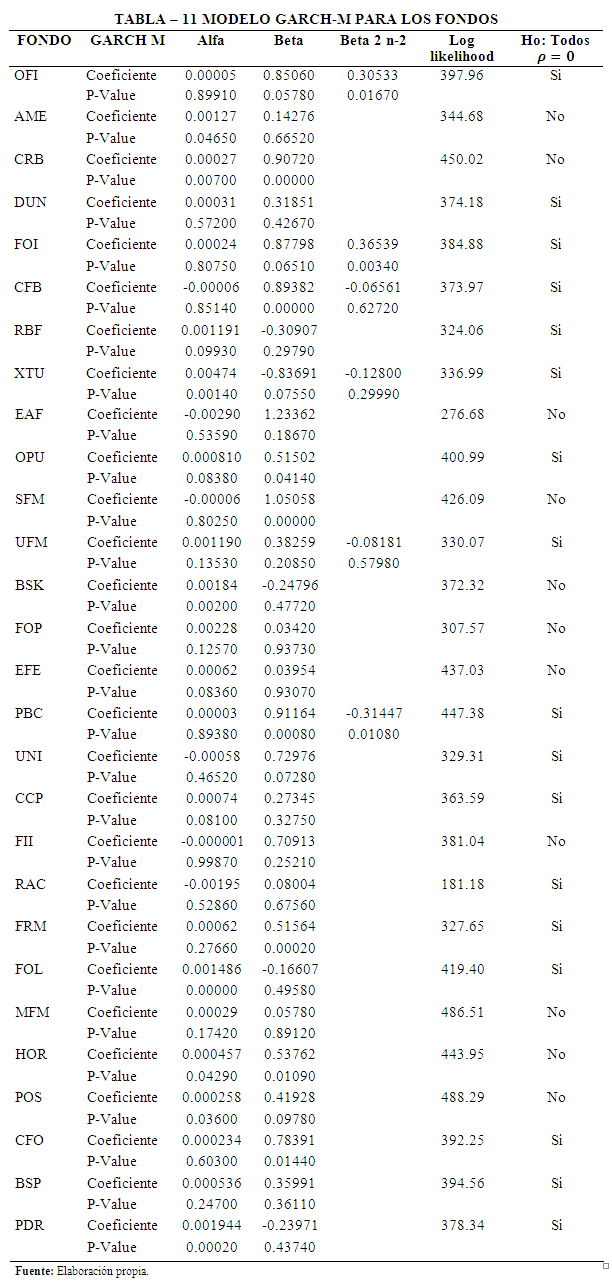
Tal y como se planteó en la ecuación (15), se realizó una estimación por mínimos cuadrados del modelo GARH-M, los resultados reflejan que en 9 Fondos fue posible estimar la rentabilidad a partir de la volatilidad correspondiente a un periodo previo, con los siguientes resultados específicos en sus coeficientes beta: OFI con Beta = 0.85, FOI con Beta = 0.88, CFB con Beta = 0.89, OPU con Beta = 0.52, PBC con Beta = 0.91, UNI con Beta = 0.73, FRM con Beta = 0.52, CFO con Beta = 0.78, finalmente XTU tiene un coeficiente Beta = -0.84, lo que se puede interpretar como una relación inversa entre el nivel de riesgo y el nivel de rentabilidad, contrariamente a lo que plantean los modelos de valoración de activos. Todos estos resultados se exponen en la Tabla 11.
4. CONCLUSIONES
En la presente investigación se logró realizar la estimación de la volatilidad de los Fondos de Inversión Abiertos del Mercado de Valores boliviano.
Mediante la aplicación del modelo GARCH (1,1) se calculó la varianza y la volatilidad condicional e incondicional (de largo plazo) mensual y anual, asimismo se realizaron proyecciones para visualizar el nivel de convergencia hacia su nivel de largo plazo, por otro lado, se implementó un proceso de simulación Monte Carlo para realizar estimaciones mediante el modelo de volatilidad estocástica, cuyos resultados fueron concordantes a los alcanzados mediante el modelo GARCH.
Se aplicó el modelo de Medias Móviles Exponenciales Ponderadas MMEP, a partir del cual también se realizaron las proyecciones respectivas para el periodo de un mes, también se pudo evaluar la presencia de asimetría en la volatilidad de los Fondos de Inversión mediante la aplicación de los modelos GJR y EGARCH, finalmente se realizó una estimación de la rentabilidad ajustada al riesgo a través del modelo GARCH-M.
Con base en todos estos modelos se pueden extraer las siguientes conclusiones:
● Los datos obtenidos mediante el modelo GARCH (1,1) muestran que los Fondos de Inversión Abiertos presentan una volatilidad mensual de largo plazo que se encuentra en el rango de 0.05% a 1.62%, mientras que la volatilidad anual se encuentra en el rango de 0.17% a 5.63%.
● En total 21 Fondos de Inversión reportaron un nivel de volatilidad incondicional anual menor al 0.90%, 5 Fondos tuvieron un nivel de volatilidad anual que se encuentra entre 1.10% y 1.74%, finalmente 2 Fondos presentaron los niveles de volatilidad más altos con 2.89% y 5.63%.
● Se determinó que 3 Fondos de Inversión presentaron una respuesta asimétrica en la volatilidad de sus rendimientos.
● Finalmente, la rentabilidad ajustada al riesgo para 9 Fondos de Inversión se traduce en una prima de riesgo que se encuentra en el rango de 0.52 a 0.91, excepto el caso de un Fondo cuya prima fue negativa.
Para investigaciones futuras se recomienda realizar estudios mediante la aplicación de un Panel GARCH, también se recomienda medir la relación que existe entre los diferentes Fondos de Inversión mediante la aplicación de modelos multivariados de varianza como ser los VECH y BEKK.
NOTAS
[1] La raíz cuadrada de la expresión (3) es conocida como la volatilidad histórica.
[2] En la teoría de la probabilidad, la media condicional o el valor esperado condicional de una variable aleatoria es su valor esperado dado que se sabe que ocurre un cierto conjunto de "condiciones" que pueden estar representadas a partir de un modelo econométrico.
[3] Por simplicidad se asume que ![]()
[4] Para comprender porque la ecuación (10) corresponde con pesos que disminuyen en forma exponencial se deberán realizan sustituciones sucesivas con los rezagos.
[5] Debido a que es un modelo más parsimonioso de la varianza condicional respecto al modelo ARCH ya que constituye un caso especial de un modelo ARCH con infinitos rezagos donde ![]() .
.
[6] Un fondo de inversión, es un mecanismo de inversión compuesto por los aportes de varios participantes, ya sean personas jurídicas o naturales, quienes forman un patrimonio común y autónomo. Este patrimonio es administrado por una Sociedad Administradora, misma que realiza inversiones en valores emitidos tanto a nivel nacional como internacional, por cuenta y riesgo de los participantes. El rendimiento de estas inversiones es distribuido proporcionalmente entre todos los participantes del Fondo. Los fondos de inversión pueden ser abiertos o cerrados. Los fondos abiertos se caracterizan por tener un patrimonio variable en el que las cuotas de participación colocadas entre el público son redimibles o rescatables directamente por el fondo en cualquier momento, siendo su plazo de duración indefinido.
[7] GIPS Global investment performance standards, son estándares éticos para ser utilizados por los gerentes de inversión para crear presentaciones de desempeño que aseguren una representación justa y una divulgación completa de los resultados de rendimiento de la inversión. Los Estándares Profesionales Globales de Inversión fueron creados por el Chartered Financial Analyst Institute y gobernados por el Comité Ejecutivo de GIPS. Son pautas estandarizadas para informar la capacidad de una empresa de inversión para obtener beneficios para los inversores.
[8] Estos Fondos se caracterizan por concentrar gran parte de sus inversiones en instrumentos de renta fija, principalmente en Depósitos a Plazo Fijo, siendo que, los Fondos en dólares tuvieron una participación promedio del 45% y los Fondos en bolivianos un 52% en este tipo de instrumento.
[9] Como señala Hull [9] para realizar esta estimación se realizó una agregación temporal basada en la siguiente relación: ![]() .
.
[10] En finanzas, los clústers de volatilidad (agrupación de la volatilidad) se definen como los grandes cambios que tienden a estar seguidos de grandes cambios, de cualquier signo, y pequeños cambios tienden a ser seguidos de pequeños cambios.
[11] El estadístico Q de Ljung-Box es el siguiente: ![]() , donde n es el número de observaciones, m es el número de coeficientes de autocorrelación y k es el rezago.
, donde n es el número de observaciones, m es el número de coeficientes de autocorrelación y k es el rezago.
[12] La hipótesis Nula establece que todas las ![]() , la Hipótesis Alterna señala que al menos un
, la Hipótesis Alterna señala que al menos un ![]() , para realizar las pruebas se utilizó la distribución Chi2 con un nivel de significación del 0.05.
, para realizar las pruebas se utilizó la distribución Chi2 con un nivel de significación del 0.05.
[13] Corresponde aclarar que el proceso de optimización fue realizado para maximizar una función objetivo que permitan alcanzar una varianza objetivo. Como señala Engle y J. Mezrich se trata de un procedimiento más robusto para estimaros parámetros en el modelo GARCH (1,1) conocido como “variance targeting”, el cual implica estimar la Varianza de Largo Plazo ![]() igual a la varianza muestral calculada a partir de los datos disponibles. Por lo tanto, el valor de
igual a la varianza muestral calculada a partir de los datos disponibles. Por lo tanto, el valor de ![]() iguala a
iguala a ![]() y solamente dos parámetros deberán ser estimados.
y solamente dos parámetros deberán ser estimados.
[14] Estos resultados se contrastan con el nivel de volatilidad de otros mercados en los cuales la volatilidad diaria se encuentra alrededor del 1% y la volatilidad anual puede ser superior al 20%.
[15] A diferencia de los otros Fondos, la rentabilidad reportada por el Fondo RAC en los últimos 4 años fue constante, este Fondo fue incluido principalmente para estimar la volatilidad generada durante la gestión 2012.
5. BIBLIOGRAFÍA
[1] C, Francq, J. M. Zakoian, GARCH Models, Structure, Statistical inference and Financial Applications, United kingdom, Wiley, 2010. [ Links ]
[2] R. F. Engle, Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation, Econometrica, Vol. 50. Issue 4, pp. 987-1008, 1982.
[3] T. G. Andersen, T Bollerslev and F.X. Diebold, Parametric and Nonparametric Volatility Measurement, Handbook of Financial Econometrics, United States of Marica, North-Holland, 2010.
[4] J. C. Hull, Estimating volatilities and correlations, Options Futures and other Derivatives, United States of America, Pearson Prentice Hall, 2009. [ Links ]
[5] T. Terasvirta, An Introduction to Univariate GARCH Models, Handbook of Financial Time Series, German, Springer, 2009. [ Links ]
[6] T. Bollerslev, R. Y. Chou, K. F. Kroner, ARCH modeling in finance, A review of the theory and empirical evidence, Journal of Econometrics, Vol. 52, pp. 5-59, 1992.
[7] Taylor, S.J. Modelling Financial Time Series, Chichester: John Wiley & Sons, 1986. [ Links ]
[8] Nelson D.B. and Cao C.Q., Inequality Constraints in the Univariate GARCH Model, Journal of Business and Economic Statistics, Vol. 10, pp. 229-235, 1992.
[9] C. Brooks, Modelling volatility and correlation, Introductory Econometrics for Finance, Cambrindge, United Kingdom, 2008.
[10] Lawrence R. Glosten, Ravi Jagannathan, David E. Runkle On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks The Journal of Finance, Vol. 48, No. 5, pp. 1779-1801, 1993.
[11] Daniel B. Nelson , Conditional Heteroskedasticity in Asset Returns: A New Approach Econometrica, Vol. 59, No. 2, pp. 347-370, 1991.
[12] Robert F. Engle, David M. Lilien, Russell P. Robins, Estimating Time Varying Risk Premia in the Term Structure, The Arch-M Model, Econometrica, Vol. 55. Issue 2, pp. 391-407, 1987.
[13] T. Bollerslev, Generalized Autoregressive Conditional Heteroskedasticity, Journal of Econometrics, Vol. 31, pp. 307-327, 1986.
[14] K. R. French, G. W. Schwert, R. F. Stambaugh, Expected Stock Returns and Volatility, Journal of Financial Economics, Vol. 19, pp. 3-29, 1987.
[15] W. Schwert, Stock Market Volatility, Financial Analyst Journal, pp. 23-34, 1990.
[16] Shannon P. Pratt, Roger J. Grabowski. Cost of capital. Cost of Capital: Workbook and Technical Supplement (2010-2011). California: Wiley; 4 edition. 2010.