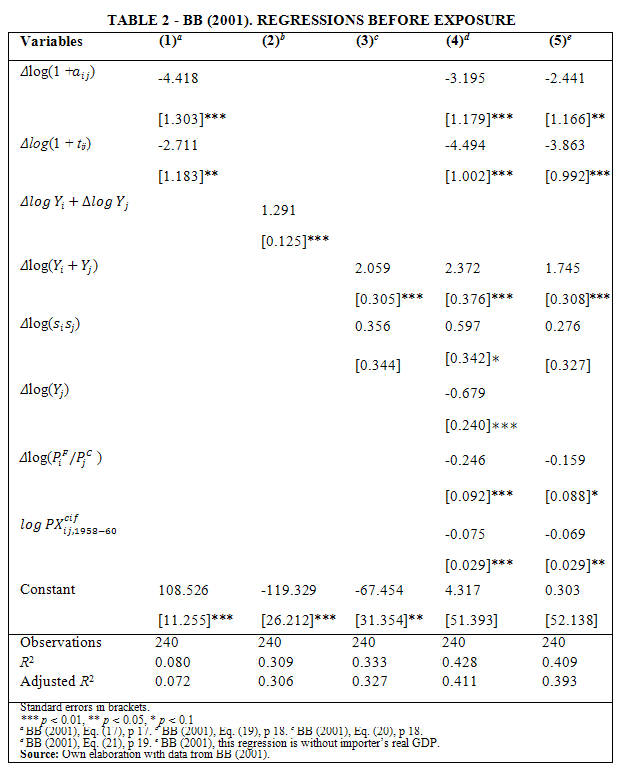Servicios Personalizados
Revista
Articulo
Indicadores
-
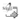 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Investigación & Desarrollo
versión impresa ISSN 1814-6333versión On-line ISSN 2518-4431
Inv. y Des. vol.2 no.17 Cochabamba 2017
http://dx.doi.org/10.23881/idupbo.017.2-1e
ARTÍCULOS – ECONOMIA Y EMPRESA
THE GROWTH OF WORLD TRADE: THE ROBUSTNESS OF THE EVIDENCE
EL CRECIMIENTO DEL COMERCIO MUNDIAL: LA SOLIDEZ DE LA EVIDENCIA
Paola L. Montero Ledezma
Centro de Generación de Información y Estadística (CEGIE)
Universidad Privada Boliviana
(Recibido el 20 noviembre 2017, aceptado para publicación el 12 diciembre 2017)
ABSTRACT
In this work we revisit the seminal paper The growth of world trade: tariffs, transport costs, and income similarity by S. Baier and J. Bergstrand published in the Journal of International Economics (2001). We develop a rigorous econometric analysis of the robustness of their results. While our findings support Baier and Bergstrand (2001)s general conclusions, we provide refined evidence of the results. Under robust estimators, we show that the presence of outliers overestimated the effect of trade liberalization and underestimated the effect of income growth, as sources of world trade growth in the second half of the past century.
Keywords: Gravity Equation, Robustness, Outliers Detection.
RESUMEN
En este trabajo revisamos el influyente artículo The growth of world trade: tariffs, transport costs, and income similarity de S. Baier y J. Bergstrand publicado en el Journal of International Economics (2001). Desarrollamos un análisis econométrico riguroso de la solidez de sus resultados. Si bien nuestros hallazgos respaldan las conclusiones generales de Baier y Bergstrand de 2001, proporcionamos evidencia depurada de los resultados. Bajo estimadores robustos, mostramos que la presencia de valores atípicos sobreestimó el efecto de la liberalización del comercio y subestimó el efecto del crecimiento del ingreso como fuentes del crecimiento del comercio mundial en la segunda mitad del siglo pasado.
Palabras clave: Modelo de Gravedad, Robustez, Identificación de Valores Atípicos.
1. INTRODUCTION
Why has world trade grown? The question raised by the Nobel Prize Laureate Paul Krugman [2] has had different reactions over the years. The following stands are clearly identified. Journalists argue that world trades growth is a response to technological progress (transport costs reduction, economists support the idea of liberalization as the main drive, and [3] and [4] argue in favor of income convergence.
Several papers have balanced the discussion in one way or another. Baier and Bergstrand [1] (henceforth BB (2001)), with over one thousand citations, bring an interesting econometric approach. The authors disentangle the relative effects of transport-cost reductions, tariff liberalization, and income convergence on the growth of world trade among several countries members of the Organization for Economic Cooperation and Development (OECD) between the late 1950s and the late 1980s. The main conclusion of their paper indicates bilateral income growth explains about 67%, tariff-rate reductions about 25%, transport-cost declines about 8%, and income convergence represents virtually none of the average world trade growth. The importance of these findings in the trade literature leads us to deepen our understanding of this seminal paper.
The aim of the present work is to revisit BB (2001)s main results under the magnifier glass of several robustness tests. For this purpose, we describe a step-by-step methodology to test the robustness of cross-sectional data utilizing graphical detection of outliers as well as high breakdown point estimators. Under various methodologies we find that BB (2001)s outcomes are sensitive to the presence of atypical points. More importantly, the share attributed to tariffs falls has been overestimated by seven percentage points and income growth has been underestimated by ten percentage points.
Many have attempted to answer Krugmans question. There is a vast literature on trade starting with [5] among others. For useful surveys see [6], [7], [8], [9]. Deepening on this literature, however, is beyond the scope of this paper. Therefore, we invite the curious reader to refer to the cited references if interested.
From the empirical viewpoint, estimating a model by means of least-squares (LS) assumes certain behavior of observations in line with an econometric model. However, in a given sample not all observations are well behaved, there might be outliers: an observation which exists at an atypical distance from other observations in a random sample from a population. If the model does not consider these atypical observations, classical methods may yield biased coefficients and standard errors. The existence of outliers is a common problem in applied research, since their presence is not known beforehand.
Outliers are classified into three categories: vertical outliers, good, and bad leverage points [10]. A vertical outlier is an observation whose dependent variable, y-dimension, is off the general trend of the rest of the data. A leverage point is an observation with an extreme value in the space of the explanatory variables, x-dimension. Leverage is a measure of how far an independent variable deviates from its mean. Leverage points are considered good if they are located closely around the regression hyperplane, and bad if they are outside of it. While bad leverage points have an important influence on the estimation of all coefficients, vertical outliers affect mostly the intercept of the regression. Moreover, they influence the slope of coefficients lightly. Finally, the effect of good leverage points is practically negligible on all coefficients [11].
Applied researchers have warned us about the effects and implications of outliers in a sample. See an overview of the literature in [12]. Among those dedicated to study vertical outliers and bad leverage points are [13], [14], and [15] for theoretical insights as well as practical applications. Good leverage points have been largely ignored. However, [16] and [17] argue that good leverage points could yield underestimated standard errors and an overestimation of the R-squared. [18] addresses these problems by suggesting measures to ensure the robustness of the goodness-of-fit of a model.
This paper is structured as follows. In section 2 we explain BB (2001)s empirical model and provide a description of the data set used. In section 3 we discuss the detection of outliers and the different methodologies to solve this problem. The empirical results are presented in section 4, where we feature the analysis of the outliers identified by several methodologies. We also compare these results with the original regression. Section 5 concludes.
2. BAIER AND BERGSTRAND (2001)
In this section we briefly review the most important features of the gravity equation, followed by BB (2001)s econometric specification. After a description of the data, we reproduce BB (2001)s outcomes.
A standard framework to study the pattern of trade is the gravity model [19]. The idea is to relate the value of bilateral flows to national income, population, distance, and contiguity (p. 8). The gravity equation is a log-linear cross-sectional specification that relates the nominal bilateral trade flow from exporter i to importer j in any year (PXij) to the exporting and importing countries nominal gross domestic products (GDPi and GDPj, respectively), distance between their economic center (Dij) and a set of dummy variables intended to reflect the existence or not of preferential trading agreement (PTAij) or of a common frontier (Aij). The basic gravity equation has the following econometric specification:[1]
![]()
where e is the natural logarithm base and εij is a log-normally distributed error term.
The empirical literature in international trade uses the typical gravity equation, whilst the novelty comes from the econometric specification as it is the case in BB (2001). In their econometric model they aim to evaluate the absolute and relative roles of real income growth, real income convergence, tariff reductions, and reductions in transportation costs, in explaining the growth of world trade between the late 1950s and the late 1980s.
The econometric model used in BB (2001) comes as a result of a general equilibrium model.[2] It develops a gravity equation with the following specification:
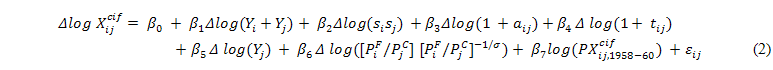
Eq. (2) is a reproduction of BB (2001)s Eq. (16), where variables are in a first-difference logarithmic form and nominal trade flows are deflated by a price index (![]() ).[3] On the purpose of studying growth, all variables are in real terms. The dependent variable,
).[3] On the purpose of studying growth, all variables are in real terms. The dependent variable, ![]() , denotes the real trade flow (the nominal c.i.f. value of the trade flow divided by the exporters deflator).
, denotes the real trade flow (the nominal c.i.f. value of the trade flow divided by the exporters deflator). ![]() i And
i And ![]() j, denote the real GDP of country i and j respectively; and
j, denote the real GDP of country i and j respectively; and ![]() ,
, ![]() denote is and js share of the two countries real incomes.[4] World income growth is captured in the constant. As explanatory variables one counts the effect of bilateral income growth, captured by variations in the term
denote is and js share of the two countries real incomes.[4] World income growth is captured in the constant. As explanatory variables one counts the effect of bilateral income growth, captured by variations in the term ![]() . Since,
. Since, ![]() is the product of real GDP shares, variation in
is the product of real GDP shares, variation in ![]() represents the effect of income convergence. Therefore, the convergence of incomes of country pairs augments trade flow growth.[5] Moreover, the effects of transport cost is captured by the gross c.i.f.-f.o.b. factor (1 +
represents the effect of income convergence. Therefore, the convergence of incomes of country pairs augments trade flow growth.[5] Moreover, the effects of transport cost is captured by the gross c.i.f.-f.o.b. factor (1 + ![]() ), while the effect of tariff-rate changes is expressed by the gross tariff rate (1 +
), while the effect of tariff-rate changes is expressed by the gross tariff rate (1 + ![]() ). Linear constraints can be evaluated for coefficient estimates of
). Linear constraints can be evaluated for coefficient estimates of ![]() and
and ![]() and nonlinear constraints for coefficient estimates of
and nonlinear constraints for coefficient estimates of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
BB (2001) assume that the elasticities of substitution in consumption (σ) and transformation of production (γ) are constant over the period of scrutiny. So, ![]() indicates whether or not the elasticity of transformation of output across markets is finite; if γ = ∞ as it is an standard assumption,
indicates whether or not the elasticity of transformation of output across markets is finite; if γ = ∞ as it is an standard assumption, ![]() s coefficient estimate will be 0. The variation in the countries relative price levels is denoted by
s coefficient estimate will be 0. The variation in the countries relative price levels is denoted by ![]() , where
, where ![]() is the standard Dixit-Stiglitz price index of landed prices and
is the standard Dixit-Stiglitz price index of landed prices and ![]() is a CET index of the firms price. Provided that the initial trade period (1958 − 60) may have had some impact on the analysis, the full model to be estimated includes, in addition, the natural logarithm of the initial periods trade flow level, log
is a CET index of the firms price. Provided that the initial trade period (1958 − 60) may have had some impact on the analysis, the full model to be estimated includes, in addition, the natural logarithm of the initial periods trade flow level, log ![]() . Last,
. Last, ![]() is a normally distributed random error term.
is a normally distributed random error term.
We use data from BB (2001), whose primarily source is the International Monetary Fund, International Financial Statistics 1995. The data set counts 240 observations and constitutes cross bilateral trade flows and economic characteristics among 16 countries belonging to the OECD. The countries are: Canada, United States, Japan, Belgium-Luxembourg, Denmark, France, Germany, Italy, Netherlands, United Kingdom, Austria, Norway, Sweden, Switzerland, Australia and Finland, here cited in decreasing order of c.i.f.-f.o.b. factors. Data is averaged over three years for the periods 1958 − 60 and 1986 − 88.
Table 1 reports a summary of the mean, standard deviation, minimum and maximum values of the growth rate (i.e., logarithmic difference) of each of the variables and the log-level of the initial periods trade flow. For instance, in 28 years the real trade flow has grown on average 148 percentage points.
The results of different specifications of BB (2001)s model are presented in Table 2, in which the dependent variable is the real bilateral trade flows from 1958 − 60 to 1986 − 88, ![]() between the countries i and j. We use ordinary least squares (LS) for all the columns. Column (1) includes as explanatory variables changes in the gross c.i.f.-f.o.b. factors and gross tariff rates over the indicated period. As expected, reducing transportation costs and tariff rates increase the growth of world trade; although the regression goodness is only 7% (adjusted R2 = 0.07). Indeed, this regression lacks of bilateral income growth as an explanatory variable.
between the countries i and j. We use ordinary least squares (LS) for all the columns. Column (1) includes as explanatory variables changes in the gross c.i.f.-f.o.b. factors and gross tariff rates over the indicated period. As expected, reducing transportation costs and tariff rates increase the growth of world trade; although the regression goodness is only 7% (adjusted R2 = 0.07). Indeed, this regression lacks of bilateral income growth as an explanatory variable.
One can begin to understand how much each variable explains of the real bilateral trade flows. For instance, multiplying the mean of the first-difference log of the gross tariff rate (-8.47) times its coefficient (-2.711) yields 23 percentage points. That means, it explains 16% of the real bilateral trade flows growth.[6] Through similar computations, the mean of the first-difference log of the gross c.i.f.-f.o.b. factors explains 11% of the bilateral trade flow growth.
Column (2) presents the estimation of a frictionless model, which is without tariffs, transportation costs, and distribution costs [20]. This model assumes complete specialization of each country in the production of one good, whose prices are normalized to unity. The gravity equation is the result of an expenditure system combined with identical homothetic preferences, and the specialization of each country in one good. Despite of improvements to the Andersons model to overcome the limited number of countries [21, 22, 27], other limitations persist, i.e., geographical considerations, transportation costs, tariff barriers. The simplicity of this model does not prevent it from reaching a higher goodness-of-fit than the previous model, with 31% of goodness (adjusted R2 = 0.31). The world output growth is 119%, and the coefficient estimate of both countries income growth is close to unity. Column (3) is also a frictionless model but decomposing the income growth (Δlog(Yi + Yj)) and the income convergence effects (Δlog(sisj)). The regression goodness is slightly higher compared to the model in Column (2) (adjusted R2 = 0.33).
The unrestricted model is presented in Column (4), which in addition to the variables in Column (3) includes transport costs, tariffs, average real GDP, income convergence, importers GDP, relative price level, and the natural logarithm of the initial periods trade flow level. This regression has a greater explanatory power (adjusted R2 = 0.41) than Columns (1), (2), and (3). All coefficient estimates are statistically significant and identical to those presented in BB (2001, p 19), except for the constant. The signs of the coefficients are the expected and therefore consistent with the theoretical model. Studying these coefficients one can conclude that three factors contribute to explaining the 148 percentage points mean growth of trade; they are: bilateral income growth, tariff rate reductions, and falls in transport-cost.
We confirm BB (2001)s outcomes regarding tariff-rate reductions which indeed explain 38 percentage points (or roughly 26%) of the trades growth.[7] Similarly, transport-costs falls explain 12 percentage points (or roughly 8%) of the growth of trade.[8]
Bilateral income growth, which is calculated by adding the remaining explanatory variables, justify about 94 percentage points[9] (or 64% of the total) of the trades growth. This result differs from the one in BB (2001) by three percentage points due to the constant coefficient, which we do not included due to its lack of statistical significance. Income convergence, although significant, has indeed a negligible contribution to explaining the mean growth of trade in this sample.
Finally, Column (5) takes into account theoretical considerations regarding elasticities of substitution in consumption and transformation of production, presented above. We regress all the variables of Column (4), except for the importers real GDP. Clearly, this regression is less suitable than the one in Column (4), with goodness-of-fit of only 39% (adjusted R2 = 0.39). Consequently, the model that better fits the data and the one that we will further study is represented in Column (4).
3. METHODOLOGY AND THEORETICAL BACKGROUND
In this section we use different methodologies suggested in the statistical and econometric literature to identify outliers and deal with them. Analyzing cross-sectional data, as stated in the Introduction, one can encounter three types of outlying observations. [10] calls them vertical outliers, good leverage points, and bad leverage points.
In this paper, vertical outliers indicate those country-pairs with atypical bilateral real trade flows which are not atypical in the space of explanatory variables. Such observations might affect the coefficient of interest as well as the intercept. Good leverage points are atypical observations in the space of explanatory variables, but located close to the regression line. For instance, country-pairs with high trade flows and also highly integrated. Those observations raise the estimated standard errors and, thus, affect the statistical inference. Finally, bad leverage points are abnormal country-pairs in the space of explanatory variables and located far away from the true regression line. For example, country-pairs with low tariff rates and low bilateral trade flows. These points would affect coefficients and the intercept.
A methodology to treat influential data consists on deleting the abnormal points one at a time, followed by the regression model using the n − 1 observations. Next, a comparison can be performed between the model with the total number of observations and the model with deleted observations. That difference provides a good idea of the influence of each atypical point deleted. To achieve this process, we must first identify the abnormal points. Here, we describe the different methodologies utilized. The classical tools are: the hat matrix, the externally and internally studentized residuals, difference in fits, difference in betas, Cooks distance, Mahalanobis distance. Furthermore, the robust estimators are: S-estimators, MCD, Hadi, L-estimator, and MM-estimator. Let us define the model of interest as:
![]()
where y is the dependent variable, X is the vector of the explanatory variables, β is the vector of regression parameters, ε is the error term, and n is the number of observations. As standard, errors are assumed to be independent of the explanatory variables and i.i.d., following a normal distribution N(0, σ2). The coefficients are generally estimated by ordinary least square (LS):
![]()
or in matrix notation:
![]()
At this point, we introduce the first method for outlier detection. The projection matrix, also known as the hat matrix,[10] or the influence matrix [29] contains information about the influence of a data y value might have on each fitted y value (ŷ) [28, 30, 31]. By multiplying each side of Eq. (3) by X, we obtain the hat matrix, denoted H.
![]()
where each fitted value is a (linear) combination of all the observed y values. That is:
.![]()
Therefore, the larger the ![]() value, the more influence
value, the more influence ![]() has on the fitted value [32]. The values
has on the fitted value [32]. The values ![]() form the hat matrix diagonal, which in case of being large it means that the ith observation is influential. Let denote the sum of the diagonal values of the hat matrix as:
form the hat matrix diagonal, which in case of being large it means that the ith observation is influential. Let denote the sum of the diagonal values of the hat matrix as:
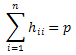
then, two rules of thumbs can be listed:
● If
> 2p/n, an observation might be worth investigating [33].
● If
> 3p/n, the leverage is large [34].
The best way to use the hat matrix diagonals is in a leverage plot. This plot puts the hat matrix diagonals on x-axis and the squared in standardized residuals on the y-axis (see Figure 1 for an application).
[35] argue that having residuals with more than three or four standard deviations away from zero are potentially outliers. For this reason, a next step is to analyze standardized residuals (![]() ) rather than raw residuals (
) rather than raw residuals (![]() ) [36]. For instance, an internally studentized residual is simple a standardized residual that writes:
) [36]. For instance, an internally studentized residual is simple a standardized residual that writes:
![]() where
where ![]() and
and ![]()
while externally studentized residual writes:
![]() ,
,
where ![]() is an estimate of σ when observation i is deleted. Both, internally and externally studentized residuals follow a t-distribution with n − p degrees of freedom [36].
is an estimate of σ when observation i is deleted. Both, internally and externally studentized residuals follow a t-distribution with n − p degrees of freedom [36].
Note that ![]() is the observed response for the ith observation. While
is the observed response for the ith observation. While ![]() is the predicted response for ith observation based on the estimated model with the ith observation deleted. Thus, the deleted residuals are
is the predicted response for ith observation based on the estimated model with the ith observation deleted. Thus, the deleted residuals are ![]() .
.
The difference in fits is the number of standard deviations that the fitted value changes when the ith case is omitted. It is defined as:
![]() .
.
An observation is regarded as influential if the absolute value of its ![]() value is greater than
value is greater than ![]() [32].
[32].
The difference in betas indicates by how much an estimated parameter changes when one single observation is deleted. An observation is influential if the absolute value of its ![]() is greater than
is greater than ![]() [32]. This indicator writes:
[32]. This indicator writes:
![]() .
.
Cooks Distance[11] is used for measuring the influence of a data point when performing a LS regression analysis. It helps identify data points that require a checking for validity, or to spot the regions where more data points are needed.
![]() .
.
Di can be interpreted as the scaled Euclidean distance between the two vectors of fitted values when the fitting is done by including or excluding the ith observation. [33, p 383]. The cut-off values for identifying influential points are widely discussed. [39] suggest Di > 1 as a cut-off point, while other authors indicated Di > 4/n, where n is the number of observations [40, 34].
Mahalanobis distances, first introduced in [41], are used to identify leverage in higher dimensions. The Mahalanobis distance of an observation ![]() from a set of observations with mean
from a set of observations with mean ![]() and covariance matrix
and covariance matrix ![]() is defined as:
is defined as:
![]() .
.
However, ![]() are not robust since they are based on classical estimations, i.e., the mean
are not robust since they are based on classical estimations, i.e., the mean ![]() and standard deviation
and standard deviation ![]() . Therefore, after some computations one can rewrite the Mahalanobis distance as:[12]
. Therefore, after some computations one can rewrite the Mahalanobis distance as:[12]
![]() .
.
[42] suggests several critical values to identify atypical points. Here, we follow [32] and use ![]() .
.
Since, classical tools for outlier identification do not guarantee an appropriate recognition and resistance to all types of outliers, high breakdown point estimators are needed. Among the robust estimators we center on the S-estimators, Minimum Covariance Determinant, Hadi method.
The S-estimator stands out due to its strong robustness and asymptotic properties. The S-estimators objective is to minimize the sum of a function of the deviations [43]. In a nutshell, the S-estimator aims to minimize another measure of the dispersion of the residuals as a robust alternative to LS, that is:
![]() .
.
This estimator finds a regression line that minimizes a robust estimate of the scale of the residuals. It is highly resistant to leverage points, and it is robust to vertical outliers. However, the S-estimators is known to be inefficient.
[44] propose the Minimum Covariance Determinant estimator (henceforth, MCD). Based on [45]s generalized variance. By seeking for the 50% subsample with the smallest generalized variance, and assuming that the subsample is outliers-free, the MCD estimator can hence be used to compute robust estimates.
[46] proposes a novel detection procedure in presence of outliers. It consists on calculating the Mahalanobis distance, but using a vector of variable medians instead of a vector of means:
![]() .
.
The idea is to sort individuals by ![]() , use the subsample with the first p + 1 points in order to re-estimate µ and Σ. Next, one must recalculate
, use the subsample with the first p + 1 points in order to re-estimate µ and Σ. Next, one must recalculate ![]() and sort the data again. If the first point is an outlier one must repeat the process until the first point is no longer an outlier.
and sort the data again. If the first point is an outlier one must repeat the process until the first point is no longer an outlier.
Heretofore, we have described outlier detection methods whose limitation is to simply identify atypical points for their elimination. Next, we introduce methodologies which deal with outliers during the process of fitting the data to the model. Among this we explain the L-estimator, the M-estimator, and the MM-estimator.
A problem with Eq.(4) consist on the excessive weight given to large residuals. LS is therefore sensitive to outliers. Several alternatives have been proposed. Let us begin with the L-estimator in which the squared function of residuals is replaced by its absolute value. That is:
![]()
The M-estimator introduced by [47], first awards a weight zero to individuals with Cook distances larger than 1.
![]()
Next, a re-descending M-estimator is computed using the iterative algorithm starting from a monotonic M-solution. Finally, σ is re-estimated at each iteration using the median residual of the previous iteration. This estimators procedure is based on iteratively reweighted least squares which work by assigning a weight to each observation and giving higher weight to better behaved observations[13] [32]. This methodology, however, uses an initial estimate as initial point to compute the weights followed by iterations to re-weight the least squares algorithm. Consequently, full robustness analysis requires high breakdown point estimators such as MM-estimators.
MM-estimators attempt to retain both the robustness and resistance of S-estimation, and at the same time gain in effciency (as with the M-estimation). The procedure is the following: (i) it finds a highly robust and resistant S-estimate that minimizes the residuals; and (ii) it holds constant the estimated scale while a M-estimate is estimated.
4. ANALYSIS
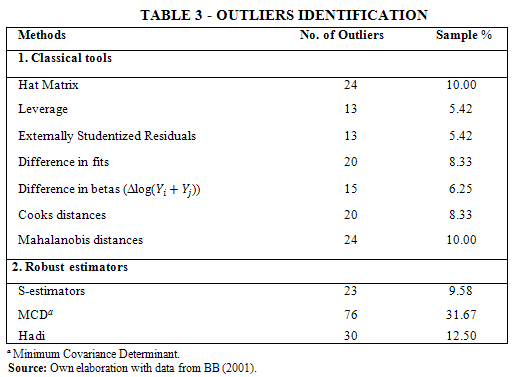
We target the regression of Table 2, Column (4), to check for the existence of outliers. We compare the results from the methodologies described in Section 3 to evaluate the robustness of these results. Following the same structure as in section 3, first, we go through classical tools for outliers identification. In this case, the percentage of outliers is between 5% and 10%. However, since these tools do not guarantee an appropriate identification and resistance to all types of outliers we move to robust estimators. Using high-break point estimators the sample presents between 10% and 32% of outliers depending on the method.
Table 3 below summarizes these outcomes. Among the classical tools to identify abnormal points, leverage and externally studentized residuals hold the lowest number of outliers as a percentage of the sample. This is because in the leverage plot large outliers might mask smaller ones. For the case of difference in betas, we pick the coefficient of the income growth, only to find 6% of outliers. We reach the same results, 10% of outliers, with the hat matrix and Mahalanobis distances. Nevertheless, none of the classical tools succeed at detecting more than 24 outliers.
There are more interesting results when we look at robust estimators. Among them, the MCDs outcome calls for further scrutiny.
● Graphical detection of outliers
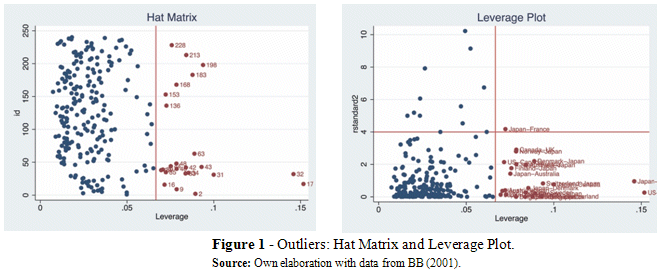
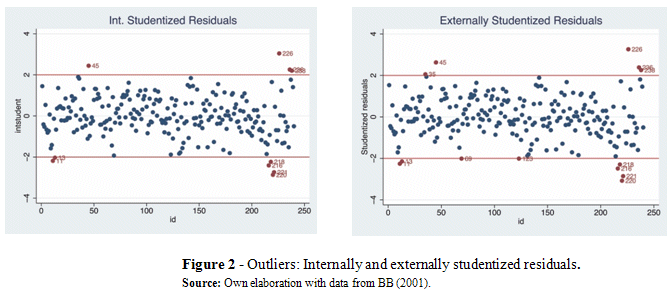
Among the classical tools used for the identification of outliers, we begin with the hat matrix and the leverage plot, see Figure 1. The observations plotted in red are leverage points; this is valid for all the following figures. The observations plotted in red are abnormal points. In both graphs, we identify the country-pairs of US-Japan (17) and Japan-US (32) as the points located furthest away from the rest of the sample.
The internally and externally studentized residuals, presented in Figure 2 establish that the atypical country-pairs Japan-France (35), Japan-Finland (45), Finland-Canada (226), Finland-Austria (236), Finland-Sweden (238). Note that not all the country-pair outliers overlap.
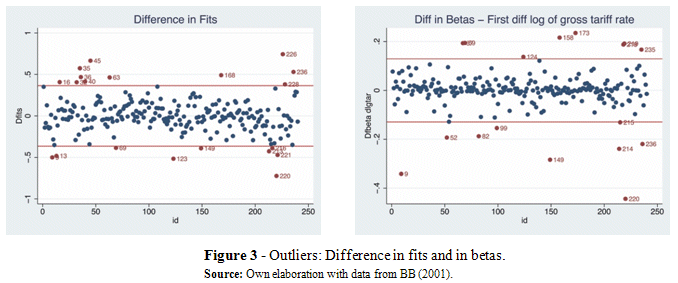
The difference in fits reveals the country-pairs of Japan-Finland (45), Finland-Canada (226), Australia-UK (220) as outliers. We study the difference in betas applied to coefficient of income growth variable, log(Yi + Yj). The country-pairs that stick out are Australia-UK (220), Norway-Italy (173), among others (see Figure 3).
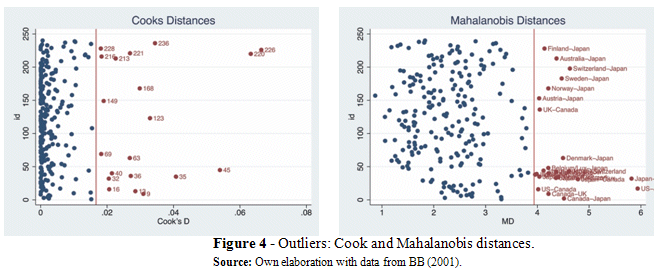
In Figure 4 we observe that according to the Cooks distance, Australia-UK (220) and Finland-Canada (226) are the country-pairs with the highest distance from the rest of the sample. While Mahalanobis distance reveals even a higher number of outliers.
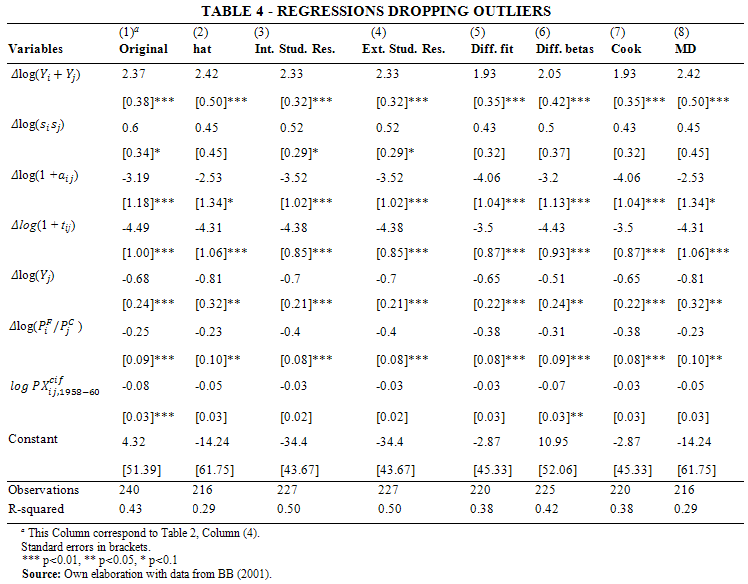
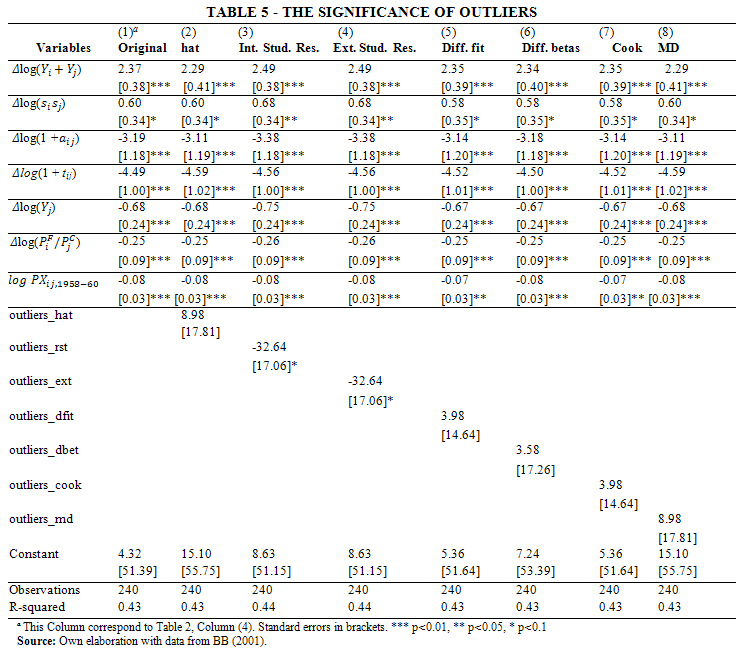
Once outliers have been spotted, according to the criteria explained above, we regress the model of interest without those outliers and compare them. Table 4 provides a complete comparison of all the regressions. Column (1) reproduces Column (4) of Table 2. Column (2) presents a regression without the outliers found with the hat matrix method. We observe that the R2 is much lower, with a value of 0.29. However, income convergence and the initial trade flow level are no longer significant. Similar results are given for Column (8), in which outliers have been pinpointed through Mahalanobis distance. The internally and externally studentized residuals yield more encouraging results, with an R2 = 0.50. However, the initial trade flow level lacks of significance. Dropping those outliers identified through difference in fits, difference in betas, and the Cooks distance do not provide better goodness-of-fit (0.38 < R2 < 0.42). Moreover, income convergence and the initial trade flow level are not significant.
The outcome of Table 4 is still unclear. Dropping a few outliers seems to deliver a higher goodness-of-fit, in some cases, but at a cost of losing significance in some explanatory variables. Therefore, Table 5 displays the same eight columns as in Table 4, but now it includes the dropped outliers as explanatory variables. The goal is to verify how important are those outliers previously discarded. Although most of the coefficients of the atypical observations are not significant, all models fit the data as well as the original model, meaning that they have similar R2. Moreover, all the parameters of the explanatory variables are statistically significant.[14] Therefore, we conclude that the atypical observations are relevant for the estimation of the model. In other words, a within transformation calls to be in place using high breakpoint estimates.
● High breakdown point estimators
We plot the Robust Standard Residuals in the y-axis versus robust Mahalanobis distances using MCD and Hadi distance methodologies, see Figure 5. The former gives an idea of the atypical data with respect to the fitted regression plane (on the y-axis), whereas the latter depicts the outlyingness of the explanatory variables (on the x-axis).
The observations plotted in red are leverage points. For instance, country-pairs like Japan-Finland (45), Japan-France (35), Norway-Japan (168), Finland-Japan (228), and Denmark-Japan (63), among others are bad leverage points as they are outliers in the horizontal as well as in the vertical dimension. Contrarily, country-pairs such as Japan-Italy (37) or Japan-UK (39) are good leverage points since they are outlying in the horizontal dimension nor on the vertical one. As mentioned in Section 3 the presence of vertical outliers and bad leverage points might distort the coefficients and the standard errors of scrutiny.
To further explore the consequences of the presence of outliers, we compare the results of Table 2, column (4) to the median regression (qreg) or L-estimator, Hubers monotonic M-estimator (rreg), and the high breakdown MM-estimator (mmregress). Table 6 presents the results after a within transformation in the data. There are differences across methodologies, and as one can observe, the presence of outliers was biasing the results, in most cases, downwards. First, note that the coefficient estimate for income convergence (log(sisj)), it seems to be unimportant in explaining world trade growth (at a 10% level) when looking at the ordinary LS and median regression (columns (1) and (2)). However, when the influence of outliers and bad leverage points are taken into account (i.e., columns (4) and (5)), it turns out to be statistically significant different from zero at 1% level. Moreover, the coefficient estimate for the initial trade flow ( ![]() ) is no longer statistically significantly different from zero.
) is no longer statistically significantly different from zero.
We study the regression threw by the MM-estimator due to its superior features. From Column (4), first, we confirm that transport-cost reduction explains 12 percentage points (or roughly 8%).[15] Second, tariff-rate reduction explains 31 percentage points (or roughly 21%).[16] That reveals an overestimation of the original results of seven percentage points. Third, we find that income convergence fall explains −2 percentage points (or roughly −2%).[17] This coefficient is significant at 1% level. Last, bilateral income growth explains 104 percentage points, or the remainder, of this trades growth (71% of the total).[18] Thus, under robust estimations income growth explains more of trade growth than previously stated, ten percentage points more.
5. CONCLUSIONS
This paper studies the robustness of BB (2001)s seminal paper. The authors argue that bilateral income growth explains about 67%, tariff-rate reductions about 25%, transport-cost declines about 8%, and income convergence represents virtually none of the average world trade growth. After briefly presenting BB (2001), we provide a step-by-step methodology for robustness checks in the presence of outliers in cross-sectional data analysis. We discuss classical methodologies for atypical points seeking such us, hat matrix, internally and externally standarized residuals, difference in fits, difference in betas, Cooks distance, and Mahalanobis distance. Among the robust estimators utilized we the L-estimator, M-estimator, and MM-estimator, the latter being the most recommended.
Overall, under MM estimation world trade can be attributed to 8% transport decreases, 21% to trade liberalization through tariffs reductions and 71% to income growth. Henceforth, even though BB (2001)s results still hold, we conclude that under de presence of outliers trade liberalization has been overestimated in seven percentage points, while income growth has been underestimated by ten percentage points.
6. ACKNOWLEDGMENTS
We are particularly grateful to Scott Baier for helpful insights of his paper and also for kindly sharing his data set. We thank an anonymous referee for constructive comments, which contributed to improving the quality of the publication.
NOTAS
[1] For formal theoretical foundations see [20], [21], [22], [23], [24], and [25].
[2] In this paper we focus on the econometric part of the BB (2001)’s paper, rather than their theoretical contribution. This econometric approach has been also used in [26].
[3] Provided that bilateral trade flow price deflators are not available, BB (2001) use nominal trade flows adjusted for changes in the firms’ price index: the exporter’s GDP deflator.
[4] For example: si = Yi/(Yi + Yj).
[5] Income convergence is monotonically positively related to sisj, which theoretically can vary from 0 to 0.25 (BB, 2001).
[6] This is the outcome of simply dividing 23 percentage points by 147.63 percentage points, taken from Table 1.
[7] The contribution of 38 percentage points is reached from the product of the mean logarithmic change of the tariff variable (-8.5 percentage points) and its coefficient estimate (4.49).
[8] The contribution of 12 percentage points is achieved from the product of the mean logarithmic change of the gross c.i.f.-f.o.b. factor (-3.6 percentage points) and its coefficient estimate (3.19).
[9] This is obtained from four factors. First, the product of the mean logarithmic of the bilateral income growth (105 percentage points) and its coefficient estimate (2.37) yields 249 percentage points. Second, the mean growth in importer income (103 percentage points) times its coefficient (-0.68) yield -70 percentage points. Third, the effect of the lagged trade flow (1108) times its coefficient estimate (-0.08) yields -0.83 percentage points. Forth, the product of GDP shares (-3.31 percentage points) times its coefficient estimate (0.59) yields -2 percentage points. Adding the results yield 249-70-83-2=94 percentage points. The contribution of income growth in BB (2001) is 100 percentage points after adding the constant, even though is not significant.
[10] The hat matrix was introduced by Tukey, John Wilder in 1972 [28].
[11]Named after the American statistician R. Dennis Cook, who introduced the concept in [37, 38].
[12]Mahalanobis distances are distributed as ![]() for Gaussian data. Observe that
for Gaussian data. Observe that ![]() . Hence,
. Hence, ![]() . For details of the proof see [32, p. 70].
. For details of the proof see [32, p. 70].
[13] Cases with Cook’s distance greater than 1 are excluded from the analysis.
[14] The constant is not significant even in the original model.
[15] The contribution of 12 percentage points is attained from the product of the mean logarithmic change of the gross c.i.f.-f.o.b. factor (-3.6 percentage points) and its coefficient estimate (-3.39).
[16] The contribution of 31 percentage points is retrieved from the product of the mean logarithmic change of the tariff variable (-8.5 percentage points) and its coefficient estimate (-3.69).
[17]The contribution of −2 percentage points is obtained from the product of the mean logarithmic change of the income convergence variable (−3.3 percentage points) and its coefficient estimate (0.75).
[18] This calculation is similar to the one presented in footnote 9.
7. REFERENCES
[1] S. L. Baier and J. H. Bergstrand, “The growth of world trade: tariffs, transport costs, and income similarity,” Journal of International Economics, vol. 53, pp. 1–27, 2001.
[2] P. Krugman, “Growing world trade: Causes and consequences.” Brookings Papers on Economic Activity, vol. 1, pp. 327–377, 1995.
[3] E. Helpman, “Imperfect competition and international trade: Evidence from fourteen industrial countries,” Journal of the Japanese and International Economies, vol. 1, no. 1, pp. 62–81, 1987.
[4] D. Hummels and J. Levinsohn, “Monopolistic competition and international trade: Re-considering the evidence,” Quarterly Journal of Economics, vol. 110, no. 3, pp. 799–836, 1995.
[5] J. Tinbergen, Shaping the World Economy: Suggestions for an International Economic Policy. The Twentieth Century Fund, New York, 1962. [ Links ]
[6] R. Baldwin, “Towards an integrated europe,” Centre for Economic Policy Research, London, 1994.
[7] V. Oguledo and C. MacPhee, “Gravity models: A reformulation and an application to discriminatory trade arrangements,” Applied Economics, vol. 26, pp. 107–120, 1994.
[8] J. Frankel, “Regional trading blocs in the world economic system,” Institute for International Economics, Washington, DC, 1997.
[9] J. Wagner, “International trade and firm performance: a survey of empirical studies since 2006,” Review of World Economics, vol. 148, pp. 235–267, 2012.
[10] P. J. Rousseeuw and A. Leroy, Robust Regression and Outlier Detection. Wiley, New York, NY, 1987. [ Links ]
[11] C. Dehon, M. Gassner, and V. Verardi, “A Hausman-type test to detect the presence of influential outliers in regression analysis,” Economic Letters, pp. 64–67, 2009.
[12] R. Maronna, D. Martin, and V. Yohai, Robust Statistics: Theory and Methods. Wiley, New York, 2006. [ Links ]
[13] P. J. Rousseeuw and B. v. Zomeren, “Unmasking multivariate outliers and leverage points,” Journal of the American Statistical Association, vol. 85, pp. 633–639, 1990.
[14] J. Temple, “Robustness tests of the augmented Solow model,” Journal of Applied Econometrics, vol. 13, pp. 361–375, 1998.
[15] J. Temple, “Growth regressions and what the textbooks don’t tell you,” Bulletin of Economic Research, vol. 52, pp. 181–205, 2000.
[16] D. Ruppert and D. G. Simpson, “Comment on Rousseeuw and van Zomeren,” Journal of the American Statistical Association, vol. 85, pp. 644–646, 1990.
[17] C. Croux, “Are good leverage points good or bad?,” in Paper Presented at the International Conference on Robust Statistics, 2006.
[18] C. Croux and C. Dehon, “Estimators of the multiple correlation coefficient: local robustness and confidence intervals,” Statistical Papers, vol. 44, pp. 315–334, 2003.
[19] B. Eichengreen and D. Irwin, “Trade blocs, currency blocs and the reorientation of world trade in the 1930s,” Journal of International Economics, vol. 38 (1/2), pp. 1–24, 1995.
[20] J. Anderson, “A theoretical foundation for the gravity equation,” American Economic Review, vol. 69, no. 1, pp. 106–116, 1979.
[21] P. Krugman, “Increasing returns, monopolistic competition, and international trade,” Journal of International Economics, vol. 9, pp. 469–479, 1979.
[22] E. Helpman and P. Krugman, Market Structure and Foreign Trade. MIT Press, Cambridge, MA, 1985. [ Links ]
[23] J. H. Bergstrand, “The gravity equation in international trade: Some microeconomic foundations and empirical evidence,” Review of Economics and Statistics, vol. 67 (3), 474–481, 1985.
[24] J. H. Bergstrand, “The generalized gravity equation, monopolistic competition, and the factor-proportions theory in international trade,” Review of Economics and Statistics, vol. 71 (1), pp. 143–153, 1989.
[25] J. H. Bergstrand, “The Heckscher-Ohlin-Samuelson model, the linder hypothesis, and the determinants of bilateral intra-industry trade,” Economic Journal, vol. 100 (4), 1216–1229, 1990.
[26] T. Bayoumi and B. Eichengreen, Regionalism versus Multilateral Trade Arrangements, ch. Is regionalism simply a diversion? Evidence from the EU and EFTA. The University of Chicago Press, Chicago, 1997.
[27] P. Krugman, “Scale economies, product differentiation, and the pattern of trade,” American Economic Review, vol. 70, no. 5, pp. 950–959, 1980.
[28] D. C. Hoaglin and R. E. Welsch, “The hat matrix in regression and anova,” The American Statistician, vol. 32, no. 1, pp. 17–22, 1978.
[29] B. W. Silverman, “Spline smoothing: The equivalent variable kernel method,” The Annals of Statistics, vol. 12, no. 3, pp. 898–916, 1984.
[30] R. Eubank, “The hat matrix for smoothing splines,” Statistics and Probability Letters, vol. 2, no. 1, pp. 9–14, 1984.
[31] J. Li and R. Valliant, “Survey weighted hat matrix and leverages,” Survey Methodology, vol. 35, no. 1, pp. 15–24, 2009.
[32] V. Verardi, Robust Regression in Stata. FUNDP (Namur) and ULB (Brussels), Belgium, 2009. [ Links ]
[33] S. Chatterjee and A. S. Hadi, “Influential observations, high leveraleverage, and outliers in linear regression,” Statistical Science, vol. 1, no. 3, pp. 379–416, 1986.
[34] V. Verardi and C. Croux, “Robust regression in Stata,” The Stata Journal, vol. 9, 439–453, 2009.
[35] D. C. Montgomery and E. A. Peck, Introduction to linear regression analysis. Wiley, 1982. [ Links ]
[36] J. B. Gray and W. H. Woodall, “The maximum size of standardized and internally studentized residuals in regression analysis,” The American Statistician, vol. 48, no. 2, 111–113, 1994.
[37] R. D. Cook, “Detection of influential observations in linear regression,” Technometrics. American Statistical Association, vol. 19, no. 1, pp. 15–18, 1977.
[38] R. D. Cook, “Influential observations in linear regression,” Journal of the American Statistical Association. American Statistical Association, vol. 74, no. 365, pp. 169–174, 1979.
[39] R. D. Cook and S. Weisberg, Residuals and Influence in Regression. New York, NY, 1982. [ Links ]
[40] K. A. Bollen and R. W. Jackman, Modern Methods of Data Analysis, ch. Regression Diagnostics: An Expository Treatment of Outliers and Influential Cases, pp. 257–291. Newbury Park, CA: Sage press, 1990.
[41] P. C. Mahalanobis, “On the generalised distance in statistics,” Proceedings of the National Institute of Sciences of India, vol. 2, no. 1, pp. 49–55, 1936.
[42] K. I. Penny, “Appropriate critical values when testing for a single multivariate outlier by using the mahalanobis distance,” Journal of the Royal Statistical Society, vol. 45, no. 1, 73–81, 1996.
[43] V. Verardi and A. McCathie, “The s-estimator of multivariate location and scatter in stata,” Stata Journal, StataCorp LP, vol. 12, pp. 299–307, June 2012.
[44] V. Verardi and C. Dehon, “Multivariate outlier detection in stata,” Stata Journal, StataCorp, vol. 10, no. 2, pp. 259–266, 2010.
[45] S. S. Wilks, “Certain generalizations in the analysis of variance,” Biometrika, vol. 24, 471–494, 1932.
[46] A. S. Hadi, “Identifying multiple outliers in multivariate data,” Journal of the Royal Statistical Society, pp. 761–771, 1992.
[47] P. J. Huber, “Robust estimation of a location parameter,” The Annals of Mathematical Statistics, vol. 35, no. 1, pp. 73–101, 1964.