Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
Compartir
Investigación & Desarrollo
versión impresa ISSN 1814-6333versión On-line ISSN 2518-4431
Inv. y Des. vol.2 no.14 Cochabamba 2014
ARTÍCULOS - ÉCONOMÍA Y EMPRESA
TERMS OF TRADE AND NON TRADITIONAL EXPORTS: A MICROECONOMETRIC ANALYSIS
TÉRMINOS DE INTERCAMBIO Y EXPORTACIONES NO TRADICIONALES: UN ANÁLISIS MICROECONOMÉTRICO
Ruth Marcela Aparicio
Doctorado en Economía y Administración de Empresas
Universidad Privada Boliviana
marcelaparicio@hotmail.com
(Recibido el 01 de septiembre 2014, aceptado para publicación el 13 de noviembre 2014)
ABSTRACT
Since 2004 some economies in Latin America, including Bolivia, have experienced an improvement in their terms of trade. In this research we investigate the causal effect of this improvement on nontraditional exports. We focus on before and after the increase in terms of trade and analyze how this improvement affects export performance. To identify this causal effect we rely on dynamic analysis and we use four different microeconometric techniques: Difference in differences, Kernel propensity score matching, difference in differences combined with propensity score matching, and synthetic control method. Each one of these improves estimation of the counterfactual outcome. Thus, this paper reviews the theory of these impact evaluation methodologies and also analyzes the way in which the theory has developed toward a more systematic methodology to construct the counterfactual. Our estimation results show that nontraditional exports would have increased if these countries had not had improvements in their terms of trade.
Palabras Clave: Mejoramiento en los Términos de Intercambio, Exportaciones no Tradicionales, Diferencia en Diferencias, Apareamiento por Índice de Propensión a participar (PSM), Diferencia en Diferencias Combinado con Apareamiento, Método de Control Sintético, Países Latinoamericanos.
RESUMEN
Desde 2004 algunos países en Latino America han experimentado una mejora en sus términos de intercambio. En esta investigación estudiamos el efecto causal de una mejora en los términos de intercambio sobre las exportaciones no tradicionales. Nos concentramos en el antes y en el después del incremento de los términos de intercambio y analizamos como esta mejora afecta a las exportaciones. Para identificar el efecto causal realizamos análisis dinámico y utilizamos cuatro diferentes técnicas microeconométricas: Diferencia en diferencias, apareamiento por índice de propensión a participar (PSM), diferencia en diferencias combinado con apareamiento y el método de control sintético. Cada una de estas metodologías mejora la estimación del resultado contrafactual, por lo que este trabajo revisa la teoría de estas metodologías de evaluación de impacto y analiza la forma en que la teoría ha desarrollado hacia una forma más sistemática en la construcción del contrafactual. Nuestras estimaciones muestran que las exportaciones no tradicionales se habrían incrementado si no hubiera existido una mejora en los términos de intercambio.
Keywords: Improvement in Terms of Trade, Nontraditional Exports, Difference in Differences, Propensity Score Matching-Difference in Differences, Synthetic Control Method, Latin American Countries.
1. INTRODUCTION
Since 2004 several Latin American countries are facing a significant and almost continuous growth in prices of raw materials, especially minerals and oil, and as a consequence, a sudden increase in export earnings. While this represents an important macroeconomic gain for these economies, it may also cause the permanent reduction of other tradable export industries. Krugman[23] points out that if these export inflows have a sufficiently long duration, the loss inthe export industries will be permanent. In the case of Bolivia, for example, before the improvement in terms of trade, 50% of total exports were nontraditional exports. As a consequence of higher commodity export prices, today 80% of total exports are gas and minerals with scarce value added, leaving the country higher exposed to international prices shocks. The problem arises when the nontraditional export sector has disappeared and a fall occurs in international prices of commodities that leaves the country worse than before.
The Dutch disease establishes a potential negative effect on competitiveness due to an appreciation of the real exchange rate, which in turns results in an increase in the relative price of other goods traded in the international market, hurting the international competitiveness of nontraditional exports. This research aims to study the causal effect of the improvement in terms of trade (ITT) on nontraditional exports.
From an empirical point of view, however, there are not studies about the size and significance of the effects of the improvement of terms of trade on exports. To measure this causal effect, this paper uses comparative case studies, which establish that the effect of an event on some outcome can be obtained comparing the evolution of outcome between the unit exposed to the event(treated unit) and the group of units that are similarto the exposed unit but that were not affected by the event (control group). Since the counterfactual does not exist, because we cannot observe nontraditional export levelsin the absence of ITT,in order to get more reliable estimationwe apply four different microeconometric methodologies: Difference in differences will identify the causal effect (DD). Kernel propensity score matching, which incorporates the role of "common support", will provide the right control group to build the counterfactual. Kernel propensity score matching combined with difference in differences (PSM-DD), as suggested by Blundell and Costa Dias, [6]will estimate the causal effect within the region of common support. Finally, synthetic control method (SCM) will construct a synthetic control unit. Each oneof these methodologies will provide an alternative approach to constructing counterfactualand will allow us to control for observable and unobservable characteristics time invariantand time variant. Then, a second purpose of this paper is to compare how robust are the estimates; how they change or improve with each methodology and how the counterfactual is constructed in each methodology.
In order to make sure that countries are not very different from each other, this paper is limited to study the impact of more favorable terms of trade on nontraditional exports in Latin American countries who share a common language, geographic proximity, and legal origin.[1]
Since 2004 resource rich Latin American countries like Argentina, Brazil, Chile, Colombia, Peru, Ecuador, Venezuela, Cuba, and Bolivia have experienced improvements in their terms of trade. From these, the ones that facea great increase in world prices are Venezuela, Bolivia, and Chile exporting oil and minerals. On the other hand, there are other countries like Mexico, Dominican Republic, Guatemala, Honduras, Nicaragua, Panama, El Salvador, Costa Rica, Paraguay, Uruguay, and Haiti that have not had any improvement.
In this research, we focus on those countries that facea great increase in world prices of oil and minerals: Venezuela, Chile and Bolivia. However, since we need to reproduce nontraditional export levels of a counterfactual country that would have been observed in the absence of ITT we exclude from our "treated countries" Chile because it is a country that has adopted an aggressive export promotion program to increase total exports. We concentrate in Bolivia and Venezuela as receiving the 'treatment" that is facing important improvements in terms of trade.
We use nontraditional export data, per capita constant gross domestic product (GDP), inflation, openness to trade, depreciation and capital formation from these countries. The analysisis for the period of 1995 to 2010.
The performance of world commodity prices and terms of trade in Latin American Countries is presented in section 2. The theory about the Dutch Disease is in section 3. A review of the main studies on international trade applying these microeconometric techniques is presented in section 4. A description of the data is in section 5. We estimate the effects of improvement in terms of trade using first a difference-in-differences approach. This empirical methodology, the model and the results are explained in section 6.The definition of an appropriate control group becomes crucial, thus we present the methodology and the results of Kernel propensity score matching and propensity score matching combined with DD which will allow us to improve the selection of the control group in section 7. Then, we use synthetic control method to build a synthetic control region, which reproduces the main characteristics of each country before the improvement in terms of trade. The methodology and the results are reported and discussed in section 8 while section 9 summarizes and concludes.
2. WORLD COMMODITY PRICES AND TERMS OF TRADE IN LATIN AMERICAN COUNTRIES.
Latin American countries rich in resources have always been exposed to commodity price shocks. In Figure 1 we observe that while in period 1980-2000 these shocks were moderate, during the years of 2000, world commodity prices have increased significantly. The real price of commodities has been growing in recent years. Since 2004, there has been an almost permanent rise, and although, a sharp declination in 2009, because of the global financial crisis, commodity prices are increasing again.
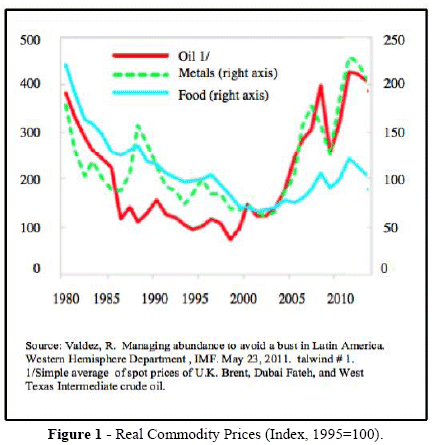
Different world events have pressed up commodity world prices. The main one has to do with the strong growth of several countries in Asia, especially China, which with an annual growth mean of 10% during the 2000's, has increased the world demand for commodities. Also, the world is facing an increasing scarcity of raw materials. This figure also shows a greater increase in prices of oil and metals and a moderate increase in food prices. This situation is reflected in significant increases in terms of trade of some Latin American countries over the last years.
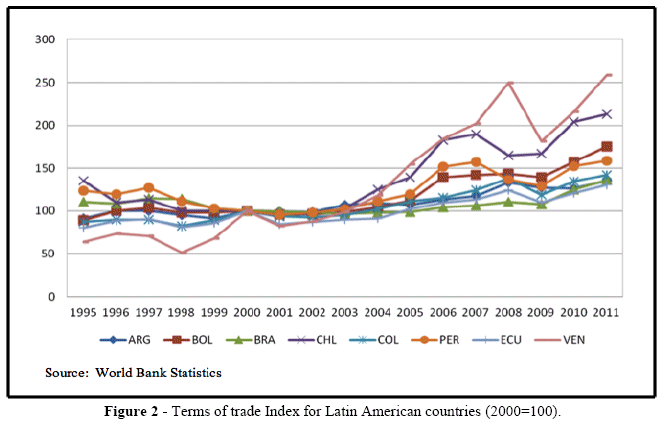
We observe in Figure 2 the terms of trade index for eight Latin American countries: Venezuela, Chile, Bolivia, Cuba, Brazil, Argentina, Peru, Colombia, and Ecuador. These countries show increases in terms of trade. However, Venezuela exporting oil, Chile copper, and Bolivia gas and minerals face increases of 150%, 110 %, and 70% in their terms of trade respectively. The other countries show lower average increases at the end of 2011.
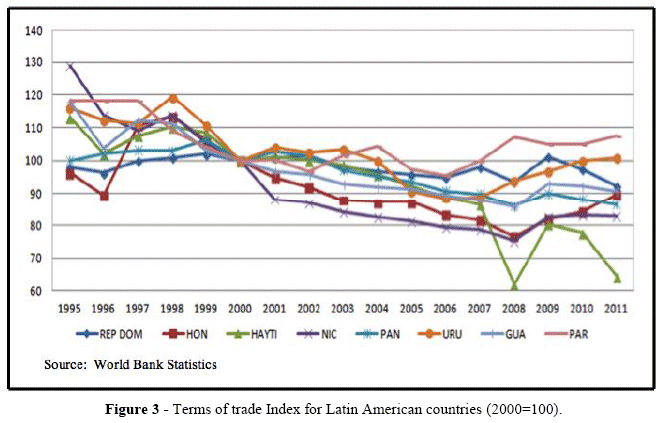
On the other hand, in Figure 3 we observe other Latin American countries: Mexico, Dominican Republic, El Salvador, Costa Rica, Panama, Honduras, Haiti, Nicaragua, Guatemala, Paraguay, and Uruguay, which over the same period have not experienced any improvement in their terms of trade or have faced a decrease in terms of trade.
2. THEORETICAL FRAMEWORK
"`The Dutch disease" studies the effects of natural resource discoveries that result in a boom in the energetic export sector or shocks like an increase in the price of a country's export, an increase in capital inflow, foreign aid, or remittances that produce an appreciation of the real exchange rate, factor reallocation and deindustrialization [25]. In this paper we focus on the effect of the increase of international prices of natural resources on other tradable export industries.
During the 1960's, Netherlands faces the discovery of reserves of oil and gas. The flow of export earnings in the economy leads to the real appreciation of the domestic currency, which cause a decline in exports of other goods. Corden [15] and Corden and Neary [16] present a specific factor model to analyze the effects of the boom in the energetic sector: The resource movement effect and the spending effect. The first one studies the movement of productive factors among sectors. Since capital is sector specific, only labor, the mobile factor goes to the booming sector, due to a higher marginal productivity of capital employed in this industry. Labor moves from the manufactured and the services sectors to the energy sector producing a decline in output of both sectors. This is called the direct deindustrialization effect and, as a result, there is a change in relative prices and a real appreciation of the currency.[2]
The increase in the flow of export earnings produces the spending effect, which leads to an increase in demand for traded and non-traded goods. In the traded market, this excess of demand will produce an increase of manufacture imports. However, since supply of services cannot increase, the adjustment in this market comes through an increase in prices of services producing a new real appreciation. As a consequence, output of services increase as labor goes from the manufactured sector producing a new decline in the output of this sector: indirect deindustrialization effect.
Buiter and Purvis [10], Enders and Herberg [18], Edwards and Aoki [17] and Van Wijnbergen [34] show that the benefits from a sudden growth of the export sector are partially counteracted by a reduction of other industries in the economy. Bruno and Sachs [9] use a model of dynamic perfect foresight equilibrium and find that the net effect of the energy sector is to reduce long run production of other tradable goods.
The persistent overvaluation of the economy results in a loss of competitiveness reducing the other tradable industries exports. According to Krugman [23], when a country discovers tradable natural resources, such as oil, it normally experiences real appreciation of its exchange rate and thus a crowding out of its other tradable sectors. He presents a model to show that for a flow of export earnings of sufficiently long duration, all of the industries moved abroad[3] will remain abroad even when the flow of export earnings ends, producing a permanent loss of the manufacturing sectors (including exports).
In recent research, Magud and Sosa [25] review over sixty papers to document potential adverse effects of Dutch Disease on long-term growth. They find evidence that shocks that trigger foreign exchange inflows lead to an appreciation of the real exchange rate generate factor reallocation, and reduce manufacturing output and net exports. In over 90%of the cases, Dutch Disease shocks generate factor reallocation and a decrease in the relative productivity of the tradable sector, and in about 75% of the cases exports are reduced.
4. EMPIRICAL STUDIES APPLYING THESE MICROECONOMETRIC METHODOLOGIES IN INTERNATIONAL TRADE.
Carl and Kruger [14] use difference in differences to study the causal effect of minimum wage increase on employment. They analyze the effect of a wage increase in New Jersey but not in Pennsylvania and compare employment in the fast food industry before and after the change in both states. They find no evidence that the rise in the minimum wage reduce employment.
There have been a few studies in international trade that use difference in differences methodology. Among the most important: Slaughter [27] that analyzes whether trade liberalizations contribute to percapita income convergence across countries. He focuses on four multilateral trade liberalizations and compares the convergence patterns among liberalizing countries and randomly chosen control countries before and after liberalization.
Pavcnik [28] identifies the impact of trade liberalization on plant productivity in the case of Chile using difference in differences and finds that trade liberalization enhances plant productivity.
Giavazzi and Tabellini [19] study empirically the effects of economic and political liberalizations on economic performance, on macroeconomic policy, and on structural policies. They find important evidence of the feedback and interaction effects between the two kinds of reforms and also those countries, which first liberalize and then become democracies do much better than countries that pursue the opposite sequence. Girma, Greenaway and Kneller [20]find a causal effect between exports and productivity increase using, for the first time, difference in differences with propensity score matching.
Abadie [3] uses synthetic control methods to evaluate the effects of the 2011 Uruguayan economic reform on foreign direct investment flows. Peluffo[29]analyzes the effect of an increased competition due to the creation of the Southern Common Market (MERCOSUR) on productivity, employment and wages for the Uruguayan manufacturing sector. She finds that increased trade liberalization seems to improve total factor productivity, reduce employment, and increase wages.
5. DATA
The sample consists of yearly data for twenty Latin American countries for the period of 1995 to 2010. Given that improvement in terms of trade occurs in 2004 we have a pre-intervention period of ten years and a post-intervention period of six years. The data collected for this research includes nontraditional export values, the outcome variable, calculated from The World Trade Organization as total exports minus exports of minerals and fuels per each country.
The set of predictors are given by per capita GDP at constant prices, investment rate as a percentage of GDP, inflation, and openness to trade, which is constructed as the sum of export and import rates as percentage of GDP. These series are obtained from World Bank database. Depreciation rate[4] is constructed as a growth rate of exchange rate series taken from Penn Tables.
Nontraditional exports and constant per capita GDP are measured in logarithm forms.
6. DIFFERENCE IN DIFFERENCES: METHODOLOGY AND RESULTS
6.1 A concept of Difference in Differences
DD is an ex post impact evaluation technique. The DD estimator measures the impact of an event or intervention by the difference between participants and nonparticipants in the before-after difference in outcomes. The important issue is to find a "counterfactual" defined as the situation a participant would have experienced had he not been exposed to the intervention. The counterfactual is the outcome in the absence of the event[24].
We observe outcomes of this event or intervention. The impact of an event can be measured by comparing actual and counterfactual outcomes but the counterfactual is not observed. According to Meyer (1995) when there is a group, for the time period before and after the event, that has not received the treatment but experiences some or all of the other influences that affect the treatment group; we can use this group as the untreated control group. The treatment effect is measured by taking the difference in outcomes between treated and control groups before and after the event or intervention. In doing so, it is important to choose a control group very similar to the treated group except in the event. Therefore, the ones who experience the event would have similar outcomes to those in the comparison group in the absence of the event.
In this research, we estimate the causal effect of the improvement of terms of trade on nontraditional exports. The improvement in terms of trade generates treatment and control groups, where Bolivia and Venezuela are the "treated countries" which have been exposed to an improvement in terms of trade. The other eleven countries that have not faced such an improvement become the group of control countries. Then, we estimate the causal effect of "the treatment" on nontraditional exports. We compare the nontraditional exports performance in the treated countries before and after the treatment with the nontraditional exports performance of the control group over the same period of time. The DD estimator will measure the change in nontraditional exports before and after the ITT experienced by treated countries and compares it to the change in nontraditional exports before and after the ITT of the control group.
In the model we have two periods. We denote the dummy variable After є{0, 1}, where After = 0 is the period before the intervention and After = 1 is the after period.
Let DIDit є{0, 1} a binary variable of weather country i experiences an improvement in terms of trade at period t. If DIDit = 1 denotes treatment and DIDit = 0 denotes untreatment.
The outcome is the change in nontraditional exports defined as: Yit. We denote ![]() and
and ![]() as the respective outcomes of the treatment and control groups in time t.
as the respective outcomes of the treatment and control groups in time t.
Cameron and Trivedi [13] establish that difference in differences will estimate the average impact as follows:
![]()
The causal effect of the improvement in terms of trade for country is defined as the change in nontraditional exports over period one if ITT occurred, less the change in nontraditional exports over the same period of time if ITT had not occurred.
The key assumption in DD is that temporal effects in treated and control countries are the same in the absence of ITT. Which means that both groups share common trends and the temporal evolution of nontraditional exports in both groups is the same. Once ITT occurs, the treated countries departure from the common trend.
One important advantage of DD is that allows for the effects of observed and unobserved characteristics on the outcome as long as they are constant in time. However, this methodology lacks a systematic approach to find similar comparison groups to treated countries.
6.2 The model
In a regression framework, the difference in differences model takes the form:
![]()
where the OLS estimate of ![]() is identical to the DD estimate.[5]
is identical to the DD estimate.[5]
The dependent variable is the natural log of nontraditional exports, where the subscript i refers to Bolivia and Venezuela and t refers to the year.
"After" is the binary time variable that takes the value of one for all the years since the improvement in terms of trade in 2004. "DID" is a binary estational variable that takes the value of one for all the countries that experienced an increase in terms of trade. "Inter" represents the interaction term of these two dummies variables showing the average treatment effect of the improvement in terms of trade on nontraditional exports and ![]() is an unobserved error term.
is an unobserved error term.
We include in the model the set of control variables Xit: per capita GDP, depreciation, inflation, investment and openness as a share of GDP.
![]()
6.3 Results from Difference in Differences estimation
To construct the counterfactual we need to choose a control group very similar to Bolivia and Venezuela except in the treatment such that the ones who experienced improvement in terms of trade would have similar outcomes to those in the comparison group in the absence of treatment. Table 1 shows Difference in Differences estimators for Bolivia and Venezuela. We experiment with different assumptions for the construction of the control group to test the robustness of our results.
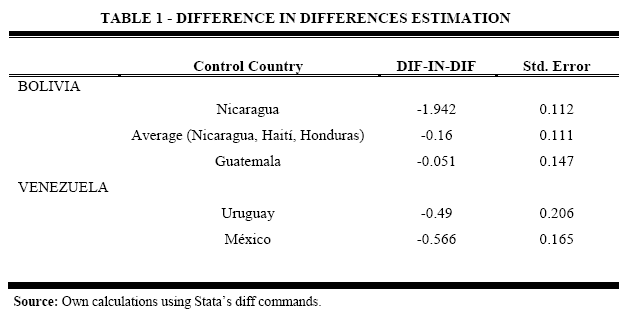
In the first row we use Nicaragua as the control country for Bolivia, which has the nearest constant per capita GDP in 1995.
In the second row we use an average of three countries as control group of Bolivia: Nicaragua, Haiti and Honduras, which have the closest constant per capita GDP. In the third row we present Guatemala as control group.[6]
In three cases the estimates identify a negative effect using clustered standard errors, showing that an improvement in terms of trade decreases non-traditional exports by as much as 2%.
To construct the counterfactual for Venezuela we use the criteria of countries with the nearest constant GDP per capita: Uruguay and Mexico. DD estimators are again negative.
To check the validity of our results we need to make sure treated and control countries share a common trend. That is, we are interested to compare countries with the same values of covariates. We apply t test at period zero and shows the means of variables for each pair of treated and control groups. Means are presented for each country along with the t statistic for the null hypothesis that the means are equal in the two countries in the pretreatment period, which is before 2004. The results show that average logexp for Nicaragua and Bolivia are similar. However, the other variables GDP per capita, inflation, capital formation, openness and depreciation for each pair of countries have a p-value less than .05 so we reject the null hypothesis in favor of the alternative hypothesis. Thus, each pair of countries is not similar and as a consequence these countries do not share a common trend.
Thus, it is not feasible to estimate an unbiased DD estimator. We conclude that there is not a systematic way to find similarities between treated and control group. Most of the time, the selection of control groups becomes very discretional and, as a consequence, unreliable to construct a good counterfactual. This is the most important weakness of Difference in Differences.
7. PROPENSITY SCORE MATCHING: METHODOLOGY AND RESULTS
7.1 Propensity Score Matching, Average treatment on the treated (ATT) and the PSM-DID estimators
Rubin [30] and Rosenbaum and Rubin [31] introduce experimental work on matching techniques. Propensity Score Matching is an alternative approach to estimate causal treatment effects and to constructing a counterfactual. According to Khandker et al.[24] the purpose of PSM is to build a counterfactual similar enough to treated countries on the basis of sufficient observable characteristics such that any two countries with the same values of these characteristics will present no systematic differences in their reactions to the treatment. Then, if each country subject to treatment can be matched with a country with the same matching variables that has not undergone the treatment, the impact of the event on a country of that type can be determined.
This matching is done using propensity score which is the probability of being part of the treatment group. We can match countries with similar propensity score from treatment and control groups.
Once we have constructed the counterfactual, we are able to estimate the "Average treatment effect on the treated" (ATT) which compares the average outcomes of treated and untreated groups and explicitly measures the effects on those who experience the event or intervention. Cameron and Trivedi [13] estimate ATT with the following equation:
![]()
Given that the counterfactual mean for those being treated is not observed we use the mean outcome of untreated individuals: E[Y(0)|DID=0]. However, this introduces a "Self-selection bias"[7], since participants and non-participants usually differs even in the absence of treatment.
To solve this selection problem and make meaningful comparisons between the outcomes of this two groups, ATT requires two assumptions. The first one is the conditional independence assumption that points out that given a set of observable characteristics of X, the outcomes are independent of treatment. That is:
![]()
This means that once we control the effects of regressors X, some of which may be related to DID, treatment and outcomes are independent. Conditional independence ensures that if the control participants were treated, their outcome, once conditioned on observable characteristics, would not differ from the expected values of outcomes of treated participants.
The second assumption is the overlap or common support condition that establishes that
![]()
This condition ensures that treatment observations have comparison observations nearby in the propensity score distribution. The common support makes sure that any combination of the characteristics observed in the treated group can be observed among the control group.
Once, Conditional Independence and Common support assumptions hold, Caliendoand Kopeinig [11],define the propensity score matching estimator for ATT as:
![]()
The mean difference in outcomes between treated and control groups over the common support appropriately weighted by the propensity score distribution of participants. Kernel propensity score matching will use weighted averages of all control countries with respect to the region of common support.
More explicitly, according to Heckman, Ichimura and Todd [22], the Treatment effect on the treated within the common support will be measured as:
![]()
where N is the number of participants and w(i,j) is the weight used to aggregate outcomes for matched nonparticipants j.
Once PSM has constructed the appropriate control group, we combine propensity score matching with difference in differences as suggested by Blundell and Costas Dias [8], to estimate Difference in Differences only for those countries that are matched using the following equation:
![]()
Where w(i; j) is the weight calculated by kernel PSM given to the jth countries in control group and matched to the ith countries in the treatment group. The estimates are more robust because we can control for observable and unobservable variables as long as they are time invariant and we can keep comparison between the treated and control groups making common trends more reliable.
7.2 Results from ATT-PSM and Kernel PSM-DD estimations
To reduce the bias and improve the construction of the counterfactual we use matching techniques. Since the change in nontraditional exports experienced by countries with ITT had they not faced an improvement in terms of trade is unobservable, we construct the counterfactual. We use countries that have similar observable characteristics in period t but did not experienced ITT. Since our objective is to build a counterfactual similar enough to Bolivia and Venezuela prior to ITT, we choose a set of predictors on basis of two principles: First, a set of macroeconomic variables that describe the level, size and structure of economic development among countries and second, a set of key variables that play an important role on competitiveness. Among the first, we use constant GDP per capita, which will control for population, investment and openness to trade both as a percentage of GDP. Among the second, we use depreciation and inflation.[8]
Propensity score matching will construct the right control group to pair Bolivia and Venezuela with similar countries on basis of these observable characteristics. Propensity score matching is the probability of receiving a given treatment conditional on some characteristics of countries before ITT.
In the case of Bolivia, to identify this probability we use a probit regression and estimate the propensity score in the region of common support which is [.01169411, .96840028]. In this area of common support we can match countries with similar propensity scores from treated and control groups. The final number of blocks is six, which ensures the mean propensity score is not different for treated and control groups on each block. We also test for balancing property of the propensity score in each variable in each block applying two sample t tests with equal variances to ensure that each variable is balanced in each block. The balancing property is satisfied. Matching has succeeded in identifying an appropriate control group.
In the case of Venezuela, we estimate the propensity score with probit regression. The region of common support is [.07290333, .86376964]. The final number of blocks is five. This number of blocks ensures that the mean propensity score is not different for treated and control groups in each block. According to Caliendo and Kopeinig[11] the common support condition is more important for kernel matching. Since we have determined the region of common support for both countries we are ready to estimate ATT.
We estimate now the Average Treatment effect on the treated (ATT) with Kernel matching method and bootstrap standard errors, Table 2.
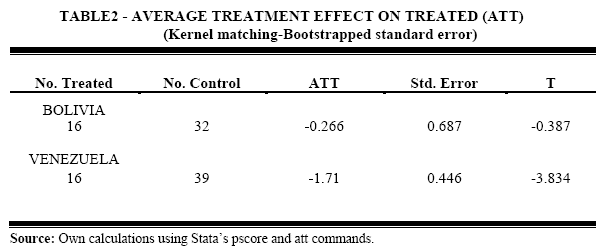
ATT estimates show a negative impact of ITT on nontraditional exports for Bolivia and Venezuela. However, the "t statistic" for Bolivia is not significant; we cannot reject the null hypothesis that the impact is equal to zero. The "t statistic" for Venezuela is statistically significant showing a negative impact of 1.71%.
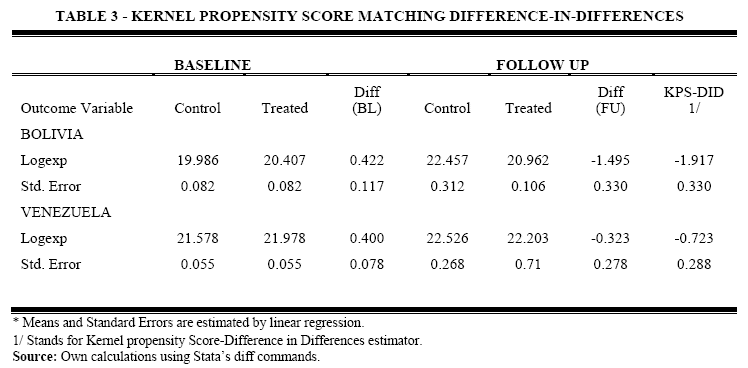
ATT estimates are still bias because do not control for unobservable omitted time invariant effects. We now combine Kernel PSM and DD estimator. Since Kernel PSM has constructed a counterfactual taking into account only those control countries that are in the area of common support with Bolivia and Venezuela, we use this counterfactual and we apply Difference in Differences. The KPS-DD estimator is more reliable.
The KPS-DD estimator for Bolivia is -1.917 with a standard error of 0.33 and the KPS-DD for Venezuela is -0.723 with a standard error of 0.288, showing a negative effect of improvement in terms of trade on nontraditional exports, Table 3. However, this methodology fails to show how the counterfactual is formed.
8. THE SYNTHETIC CONTROL METHOD: METHODOLOGY AND RESULTS
8.1 The synthetic control method
Abadie and Gardeazabal [1] propose a synthetic control method to study the effects of the terrorist conflict in the Basque Country using other Spain regions as comparison group. They provide a systematic way to choose comparison groups and to reduce discretion in the selection of the control group. They consider that a combination of unaffected units provide a more appropriate comparison than any single unaffected unit alone. They construct a "synthetic control" defined as a weighted average of unaffected units chosen to resemble the pre-characteristics of the affected unit before the treatment or intervention.[9]
The synthetic control can be represented by a set of weights attached to the unaffected units:
![]()
![]()
Where ![]() for t > T0 is the counterfactual outcome that shows how the outcome would have evolved in the affected country in the absence of intervention.
for t > T0 is the counterfactual outcome that shows how the outcome would have evolved in the affected country in the absence of intervention.
Given a set of weights wi, the treatment effect of country i in period t is given by the synthetic control estimator:
![]()
where ![]() is the outcome of country i in period t in the presence of treatment. Since this is observed, SCM reduces to a method that estimates
is the outcome of country i in period t in the presence of treatment. Since this is observed, SCM reduces to a method that estimates ![]() , which is given by a common factor model:
, which is given by a common factor model:
![]()
Abadie, Diamond, and Hainmueller [2] propose to choose a set of weights:
![]()
that minimizes:
![]()
where the weights v1,....,vk show the relative importance of the synthetic control reproducing the values of the predictors X11,...,Xk1.
According to Abadie et al. [2] the synthetic control method has attractive features: makes explicit, first, the relative contribution of each control unit to the counterfactual; second, the similarities between the treated group and the synthetic control in terms of preintervention outcomes. Third, it extends DD framework allowing that the effects of unobserved variables on the outcome vary with time.
8.2 Results from Synthetic Control Method estimation
First, we construct a synthetic Bolivia as a combination of other Latin American Countries that reproduce the values of economic predictors for Bolivia before improvement in terms of trade, in order to replicate nontraditional exports trends that Bolivia would have had in the absence of ITT. Table 4 shows that synthetic Bolivia is a weighted average of Mexico, Paraguay, Nicaragua, and Haiti. All other countries of the control group have zero weights.

Table 5 shows that Synthetic Bolivia approximates the characteristics of Bolivia prior 2004. Synthetic Bolivia is very similar to the actual Bolivia in terms of nontraditional exports, GDP per capita, inflation and depreciation. However, Synthetic Bolivia cannot replicate accurately openness and investment share. According to Abadie et al.[2], the root mean square predictor error (RMSPE) measures the magnitude of the gap in the outcome variable of each country between each country and its synthetic counterpart. The lower the RMSPE the better the fit between real and synthetic Bolivia. In this case RMSPE = 0.089 shows a good fit between real and synthetic Bolivia prior to the improvement in terms of trade.
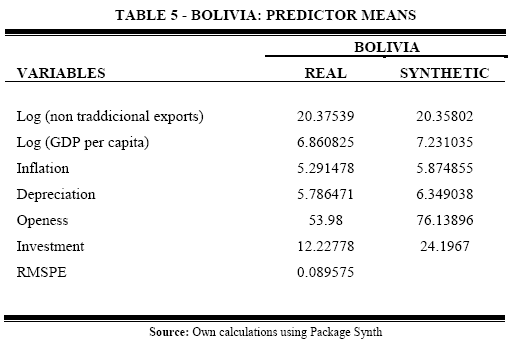
The effect of ITT will be measured by comparing the actual and counterfactual trends in nontraditional exports of Bolivia. Figure 4 shows the nontraditional exports trajectory of real and synthetic Bolivia. Synthetic Bolivia reproduces the pre-2004 nontraditional exports trend for Bolivia before the improvement in terms of trade. This close fit is reflected in the RMSPE. The effect of improvement in terms of trade on nontraditional exports is immediate. Nontraditional exports of Synthetic Bolivia are higher than the actual Bolivia showing an important negative effect ITT on exports until the end of 2010.
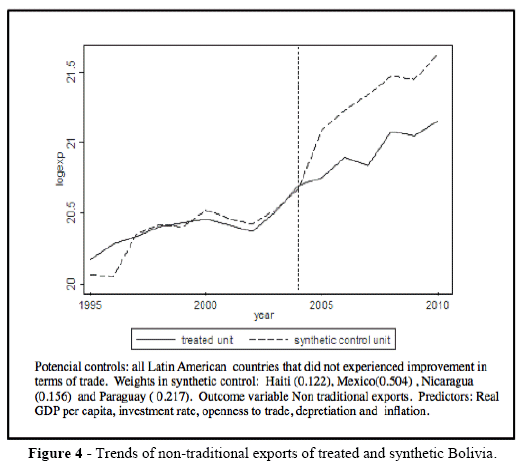
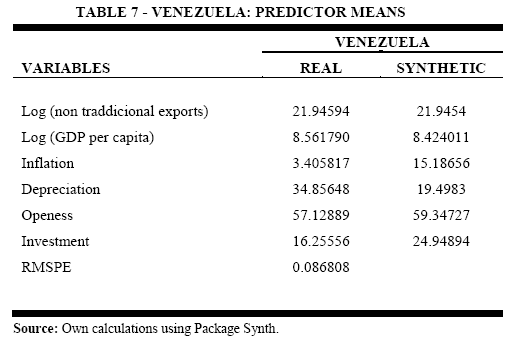
Table 6 shows synthetic Venezuela as a weighted average of Uruguay, Honduras, Panama, and Nicaragua. Table 7 shows that Synthetic Venezuela approximates well some characteristics Venezuela prior 2004 like nontraditional exports, constant GDP per capita, investment and openness. However Synthetic Venezuela cannot replicate the values for inflation and depreciation. Mainly, due to Venezuelas inflation process since 2006, this has affected the exchange rate growth. The RMSPE= 0.086 shows a small gap between real and synthetic Venezuela.

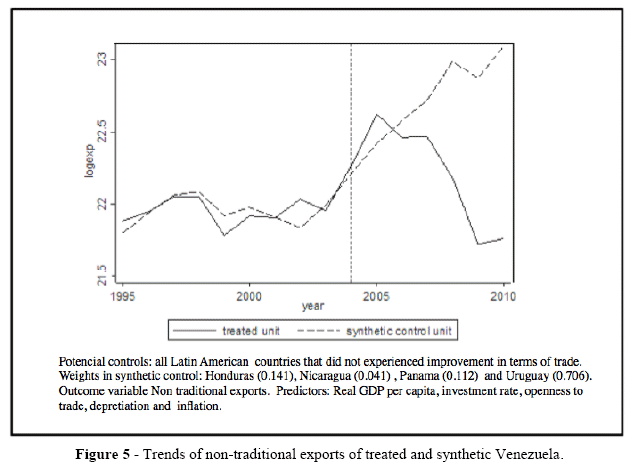
The effect of ITT will be measured by comparing the actual and counterfactual trends in nontraditional exports of Venezuela. Figure 5 shows that Synthetic Venezuela reproduces the pre-2004 nontraditional exports trend for Venezuela before the improvement in terms of trade. The effect of ITT on nontraditional exports is immediate. Nontraditional exports of Synthetic Venezuela are higher than real Venezuela revealing an important negative effect ITT on exports until the end of 2010.
9. CONCLUSIONS
In this research we analyze empirically the causal effect of improvement in terms of trade on nontraditional exports. We find that nontraditional exports present a reduction after Bolivia and Venezuela experienced an improvement in their terms of trade. This conclusion is robust to the use of fourmicroeconometric methodologies.
We also contrast these methodologies and we find that each one contributes to a more systematic construction of counterfactual. Difference in Differences estimates the causal effect in a right way when the counterfactual is similar enough to the treated unit. However, this is not always the case because the definition of counterfactual is discretional. Kernel propensity Score Matching succeeds in identifying the right control group in the region of common support. When we apply DD combined with propensity score matching we are able to find weighted averages of all control countries as match with respect to the region of common support. However we cannot find these weights.
Synthetic control method provides a more systematic mechanism to construct comparison countries, and is able to bring the list of countries that form the control group. Thus, it can be used as a complement to the other microeconometric techniques.
Difference in Differences alone or combined with Kernel propensity score matching can control for unobservable effects as long as they are constant. Synthetic Control Method extends DD framework allowing that the effects of unobserved variables on the outcome vary with time. Thus, SCM improves estimations controlling for unobserved time invariant and time variant.
When it is not feasible to get unbiased estimators with DD, ATT, and KPSM-DD because we cannot comply with strong assumptions of common trends and conditional independence, Synthetic control method still can bring a good estimation. Moreover, estimations in SCM are more significant than in the other three methodologies.
The most important empirical finding of this paper is that nontraditional exports of Bolivia and Venezuela would have increased if these countries had not experienced improvement in their terms of trade. The size and significance of the result are statistically significant and confirms what the theory says about the effect of improvement in terms of trade on nontraditional exports.
10. REFERENCES
[1] A. Abadie and J.Gardeazabal. The Economic Costs of Confict: A Case Study of the Basque Country. The American Economic Review,vol. 93, no. 1,pp113-132, 2003.
[2] A. Abadie et al.Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California's Tabacco Control Program.Journal of the American Statistical Association,vol. 105, no. 490, pp 493-505, 2010.
[3] A. Abadie. Using Synthetic Controls to Evaluate an International Strategic Positioning Program in Uruguay: Feasibility, Data Requirements, and Methodological Aspects. Draft. 2011. [ Links ]
[4] O. Blanchard. Macroeconomía. Primera Edición. España:Prentice Hall,1997.
[5] BID. Curso de Evaluacion de Impacto de Proyectos. Ministerio de Economîa de la Provincia de Buenos Aires, Argentina. 21 y 22 de abril de 2010.
[6] A. Billmeier and T. Nannicini. Trade Openness and Growth: Pursuing Empirical Glasnost. Middle East and Central Asia Department. IMF Working Paper, vol. 7, no. 156, 2007.
[7] R. Blundell and M. Costa Dias.Evaluation Methods for Non-Experimental Data. Fiscal Studies, vol. 21, no. 4,pp 427-468, 2000.
[8] R. Blundell and M. Costa Dias. Alternative Approaches to Evaluation in Empirical Microeconomics, University College London and Institute for Fiscal Studies, 2008.
[9] M. Bruno and J. Sachs.Energy and Resource Allocation: A dynamic model of the Dutch Disease. Review of Economic Studies XLIX, pp.845-859, 1982.
[10] W. Buiter and D. Purtvis. Oil, Desinflation and Export Competitiveness. A model of the Dutch Disease. National Bureau of Economic Research. Working Paper 592,1980.
[11] M. Caliendo and S. Kopeinig. Some Practical Guidance for the Implementation of Propensity Score Matching. Discussion papers Series. Forschungs Institut zur Zukunft der Arbeit, Institute for the Study of Labor, 2005.
[12] C. Cameron and P. Trivedi. Microeconometrics Using Stata. Texas: Stata Press, 2009.
[13] C. Cameron and P. Trivedi. Microeconometrics: Methods and Applications, 1st ed., New York:Cambridge University Press, 2005.
[14] D. Card and A. Krueger.MinimumWages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania.American Economic Review, vol.84, pp 772-93, 1994.
[15] M.Corden. Booming Sector and Dutch Desease economics: survey and consolidation. Oxford Economic Paper,vol. 36, no. 3, pp 356, 1982.
[16] M. Corden and P. Neary.Booming Sector and De-Industrialization in a Small Open Economy.The Economic Journal, vol. 92, no. 368, pp. 825-848, 1982.
[17] S. Edward and M. Aoki.Oil export boom and Dutch disease: A dynamic analysis. Resources and Energy, Elsevier,vol. 5, pp 219-242, 1983.
[18] K. Enders and H. Herberg.The Dutch Disease: Causes, Consequences, Cures and Calmatives.Weltwirtschaftliches Archiv Bd. 119 H.3, pp 473-497, 1983.
[19] F. Giavazzi and G. Tabellini. "Economic and Political Liberalizations." NBER Working Papers Series. Working Paper 10657, 2004.
[20] S. Girma et al. Export market exit and performance dynamics: a causality analysis of matched firms. Economics letters, vol. 80,pp 181-187, 2003.
[21] J. Hainmueller and A. Diamond. Package Synth. Software, htm. Harvard University, 2013.
[22] J. Heckman et al. Matching as an Econometric Evaluation Estimator.Review of Economic Studies, vol. 65, pp. 261-294, 1998.
[23] P. Krugman. The narrow moving ban, the dutch disease, and the competitive consequences of Mrs.Thatcher. Notes on Trade in the Presence of Dynamic Scale Economies.Journal of Development Economics, vol. 27, pp.41-55, 1987.
[24] S. Khandker et al. Handbook on impact evaluation:Quantitative methods and practices. Washington: World Bank,2010.
[25] N. Magud and S. Sosa.When and Why Worry About Real Exchange Rate Appreciation? The Missing Link between Dutch Disease and Growth.IMF Working Paper, vol. 10, no. 271, 2010.
[26] B. D. Meyer. Natural and quasi-experiments in economics. Journal of Business & Economic Statistics, vol. 13, no. 2, pp. 151, 1995.
[27] M. Slaughter. International Trade and Per Capita Income Convergence: A Difference-in-Differences Analysis.NBER. Working Papers Series. Working Paper 6457, 1998. [ Links ]
[28] N. Pavcnik.Trade liberalization, exit and productivity improvements: Evidence from Chilean plants.NBER. Working Papers Series. Working Paper 7852, 2000. [ Links ]
[29] A. Peluffo.Apertura Comercial, productividad, empleo y salarios: Un Analisis de Diferencia en Diferencias. Universidad de la Republica, Facultad de Ciencias Economicas y de Administracion, Instituto de Economia, Uruguay, 2012.
[30] D. Rubin.Estimating causal effects of treatments in randomized and nonrandomized studies.Journal of Educational Psychology,vol. 66, no. 5, pp. 688-701, 1974.
[31] P. Rosenbaum andD. Rubin. The central rol of the propensity score in observational studies for causal effects. Biometrika, vol. 70, no. 1,pp. 44-55, 1983.
[32] R. Valdez.Managing abundance to avoid a bust in Latin America. Western Hemisphere Department. International Monetary Fund, 2011. [ Links ]
[33] J. Villa.Simplifying the estimation of Difference in Differences treatment effects with Stata. Brooks World Poverty Institute,University of Manchester, 2012. [ Links ]
[34] S. Wijnbergen. The Dutch disease: A disease after all?.The Economic Journal, vol. 94, no. 373, pp 41-55, 1984.
NOTAS
[1]According to Billmeier and Nannicini [6] these variables are region-specific.
[2]For Corden [15] and Corden and Neary [16] real exchange rate is a relative price of traded goods in terms of non-traded goods. Once deindustrialization effect occurs, there is also a movement of labor out of the service sector which leads to a fall in the output of services. The authors assume that income elasticity of demand for services is zero. Hence, at the initial real exchange rate, the resource movement effect leads to excess demand for services, therefore, there must be a real appreciation to restore equilibrium.
[3]Krugman[23] presents a model of dynamic comparative advantage. He considers that Dutch Disease treats income earned in the natural resource sector much as if it were a pure transfer payment from abroad. He proves that a larger transfer will raise the recipient's relative wages, which will be enough to offset its productivity advantage so that some industries will move abroad.
[4]Blanchard [4] points out that a depreciation of domestic currency is a reduction of its price expressed in terms of foreign currency. When domestic currency depreciates, the nominal exchange rate increases.
[5]Cameron and Trivedi [13] point out that this equation for the treated group in the pre-intervention period is:
![]() =
= ![]() +
+ ![]() +
+![]() while in the post intervention will become:
while in the post intervention will become: ![]() =
= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+![]() . Therefore the impact effect is:
. Therefore the impact effect is: ![]() =
= ![]() +
+ ![]() +
+![]() -
-![]()
For the untreated group the pre-intervention equation is: ![]() =
= ![]() +
+ ![]() and for the post intervention period:
and for the post intervention period:
![]() =
= ![]() +
+ ![]() +.
+.![]() . Then
. Then ![]() -
-![]() =
=![]() +
+![]() -
-![]() .
.
Taking the difference between treated and untreated groups:![]() ) -
) - ![]() -
-![]() ) =
) = ![]() +
+![]() -
-![]() -
- ![]() -
-![]() .
.
Assuming that E [![]() -
-![]() -
- ![]() -
-![]() = 0 we get an unbiased estimate
= 0 we get an unbiased estimate ![]() identical to the DD estimate.
identical to the DD estimate.
[6]Billmeier and Nannicini [6] establish that the control country for Bolivia is Guatemala for period 1981-90.
[7]We observe that: E[Y(1)|DID=1] - E[Y(0)|DID=0] = ATT + E[Y(0)|DID=1]-E[Y(0)|DID=0]. The difference between the left had side of this equation and ATT is called the "Self-selection bias". ATT is only identified if E[Y(0)|DID=1]-E[Y(0)|DID=0] =0.
[8]Blanchard [4] defines the real exchange rate, an indicator of the competitiveness, as the relative price of foreign goods in terms of domestic goods. It is measured by: ![]() = E * P*/ P. Where E is the nominal exchange rate, P*stands for foreign prices and P represents domestic prices. A depreciation of domestic currency, holding all other variables constant, will improve competitiveness. On the other hand, an increase in domestic prices will deteriorate competitiveness.
= E * P*/ P. Where E is the nominal exchange rate, P*stands for foreign prices and P represents domestic prices. A depreciation of domestic currency, holding all other variables constant, will improve competitiveness. On the other hand, an increase in domestic prices will deteriorate competitiveness.
[9]According to Abadie and Gardeazabal [1], this approach is related to statistical matching methods.