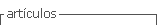Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Economía Coyuntural
versión impresa ISSN 2415-0622versión On-line ISSN 2415-0630
Revista de coyuntura y perspectiva v.6 n.1 Santa Cruz de la Sierra mar. 2021
ARTICLES ACADEMICS
Crecimiento con densidad residencial, alquiler
de tierras y valor de la tierra
Growth with residential density, land rent
and land value
Wei-Bin Zhang λ
λ Ritsumeikan Asia Pacific University. Japan.
Contacto: wbz1@apu.ac.jp
Recepción: 10/11/2020 Aceptación: 24/02/2021
Resumen
Gran acumulación de capital, rápida urbanización, y el aumento de los precios de la tierra son los principales personajes de las economías modernas. Este estudio examina estos fenómenos dentro de un marco integrado sobre la base de la teoría del crecimiento económico, economía espacial y economía urbana. Construye un modelo de crecimiento espacial con distribución residencial mediante la integración de los modelos de crecimiento de Solow y residencial de Alonso para proporcionar algunas ideas sobre los mecanismos económicos. Una característica única del estudio es determinar de forma endógena el valor de la tierra y la renta con interacciones entre la acumulación de riqueza, servicios, terrenos y condiciones de transporte. Simulamos el movimiento de la economía en el tiempo y el espacio. Realizamos análisis dinámico comparativo con respecto a la productividad total del sector productivo, condiciones de transporte, comodidades y preferencia. El documento demuestra cómo el crecimiento económico, distribución residencial, elección de cartera, y la renta y el precio de la tierra interactúan en el tiempo y el espacio.
Palabras clave: Valor del suelo, crecimiento económico, alquiler de vivienda, distribución residencial.
Asbtract
Huge capital accumulation, speedy urbanization, and rising land prices are main characters of modern economies. This study examines these phenomena within an integrated framework on basis of economic growth theory, spatial economics, and urban economics. It builds a spatial growth model with residential distribution by integrating the Solow growth and Alonso residential models to provide some insights into the economic mechanisms. A unique feature of the study is to endogenously determine land value and rent with interactions between wealth accumulation, amenity, land, and transportation conditions. We simulate the motion of the economy over time and space. We carry out comparative dynamic analysis with regards to the total productivity of the production sector, transportation conditions, amenity, and preference. The paper demonstrates how economic growth, residential distribution, portfolio choice, and land rent and price interact over time and space.
Keywords: Land value, economic growth, housing rent, residential distribution.
Clasificación JEL: E13, R11, D31.
INTRODUCCIÓN
The purpose of this study is to develop a spatial economic growth model with residential amenity and location and land value in a perfectly competitive framework. We integrate the Solow growth model (Solow, 1956), the Alonso residential models (Alonso, 1964), and Zhang's recent work on introducing determination of land value in the neoclassical growth theory (Zhang, 2016). A unique contribution of the study is to determine dynamic interdependence between land value, land rent, wealth accumulation, amenity, land use, and transportation conditions.
The necessity of analyzing urban configuration and economic growth as a connected whole has long been recognized (for instance, Lucas, 1988; Henderson and Thisse, 2004; and Capello and Nijkamp, 2004). As early as in 1980, Arnott (1980: 53) points outs: "In the last decade the static theory of residential urban location and land use has been extensively developed. The theory has generated many useful insights, but because it ignores growth and durability of housing and urban infrastructure there are many urban phenomena it cannot explain." This description is still applicable to (most of) the current literature of urban economics. On basis of Zhang's work (2002, 2008), we introduce neoclassical economic growth theory with capital accumulation to the standard land-use model of the urban economics and regional science. The growth mechanism of our model is based on the Solow growth model. It is well known that the development of the neoclassical growth theory is strongly influenced by the pioneering works of the two similar models separately proposed by Solow and Swan in 1956 (Solow, 1956; and Swan, 1956). In the literature the Solow-Swan model is often referred to as the Solow model. The Solow model considers capital and labor as substitutes for one another. The model assumes full employment of the input factors. There are numerous extensions and generalizations of the model (Burmeister and Dobell, 1970). The production side of our model is based on the neoclassical growth approach to urban growth and dynamics (e.g., Richardson, 1973, Rabenau, 1979, Henderson, 1985). We apply an alternative approach to consumer behavior proposed by Zhang (1993).
Following Zhang (2008), we apply the Alonso model to describe the spatial character of our economy. Like the Solow model in the neoclassical growth theory, the Alonso model plays a key role in the development of neoclassical urban economics (Alonso, 1964). The earlier important contributions are made by Muth (1969), Mills (1967), Beckmann (1969), Solow (1973), and others. Many studies in urban economic examine spatial structure of urban areas on the influence of the Alonso model (Mills, 1967; Muth, 1969; Fujita, 1989). As pointed out by Zhang (2002), most of the models concentrate on the residential location and urban structure and neglect production aspects of urban dynamics. Most of these studies are limited to comparative steady state analysis. They are focused on urban economic structures in static frameworks without wealth accumulation and land value determination. The main purpose of this study is to introduce endogenous land value and wealth accumulation. Leung and Teo (2011) observe that one of stylized facts on regional economic variation is related to the real estate markets. As land is an alternative way of making saving for future consumption, a proper economic model should take account of portfolio structures. Brueckner (1987) builds an urban model, taking account of the idea that commuting costs within an urban area are related to differing housing prices. The model explains the internal structure of cities as well as intercity differences in spatial structure. Sato and Xiao (2015) propose a model of interactions between labor and land markets in a city. These studies do not include portfolio equilibrium between different assets with a genuine dynamic framework as capital accumulation, which is the main determinant of economic growth, is not taken into account in urban spatial formation. As argued by Brito and Pereira (2002), the link between the housing market and long-term growth has been neglected in the literature. This study makes a contribution to linking housing market and economic growth. In association with modern economic growth and structural changes, the complexity of portfolio is increased (e.g., Uhler and Gragg, 1971; Agell and Edin, 1990; Cobb-Clark and Hilderbrand, 2009; Gaudecker, 2015). Households of contemporary economies are characterized of many assets such as housing, land, stocks, precious metals, gold, cashes in different currencies in their portfolios. As summarized in the overview by Guiso et al. (2002), "Until recently, researchers in economics and finance paid relatively little attention to household portfolios. Reasons included the tendency of most households to hold simple portfolios, the inability of the dominant asset pricing models to account for household portfolio incompleteness, and the lack of detailed databases on household portfolios in many countries until the late 1980s or 1990s. Now, however, the analysis of household portfolios is emerging as a
field of vigorous study." As recently reviewed by Liu etal. (2011: 1), "Although it is widely accepted that house prices could have an important influence on macroeconomic fluctuations, quantitative studies in a general equilibrium framework have been scant." In the contemporary literature on land and economic growth only a few studies are concerned with determining land value, residential location and economic growth with microeconomic foundation. Our study proposes a mathematical model to deal with growth with portfolio choice equilibrium with land and physical capital within a comprehensive analytical framework with time and space.
It is well recognized that development of transportation systems has important effects on housing market, land rent, and residential distribution. This study also introduces transportation into the growth model with land value. The need for developing analytical frameworks for examining spatial economic growth with amenity is well recognized. We introduce amenity into the neoclassical growth theory in a spatial context. Issues related to interdependence between economic growth and amenity have been examined in the economic literature. There are many studies about amenities (Tiebout, 1956; Oates, 1969; Rosen, 1979; Roback, 1982; Beeson Gabriel et al. 2003; Chen and Rosenthal, 2008; Albouy and Lue, 2015). Nevertheless, only a few attempts have been made to introduce amenity into formal dynamic economic analysis with rational assumptions of profit and utility maximization in urban economics. It is well recognized that location choice is closely related to the existence and quality of such physical environmental attributes as open space and noise pollution as well as social environmental quality. Earlier introduction of amenities into spatial economics with microeconomic foundation is carried out by Zhang (1993a). As argued by Glaeser et al (2001), consumption amenities have increasingly played more important role in urban formation. Public services, accessibilities, local transportation systems, pollution, and human relations such as discrimination all involve externalities and affect amenities. In this study, we incorporate amenity into the consumer location decision by assuming that amenity is a function of residential density.
This study deals with issues related to growth, transportation systems and residential distribution in a comprehensive framework. We study dynamic interactions between capital accumulation, land, housing, amenity, transportation in an isolated linear economy, by synthesizing the main ideas in the Solow growth model in the neoclassical growth theory and the Alonso urban model with an alternative approach to household behavior proposed by Zhang. The model is a one-dimensional model of residential location with a central business center (CBD). The paper is a synthesis of the two models proposed by Zhang (2008, 2016, 2018). The main differences from the two models are that Zhang (2008) includes growth mechanisms and residential distribution without taking account of land value and without dynamic analysis and Zhang (2016) deals with portfolio equilibrium between land and physical wealth without taking account of residential location. Zhang (2018) deals with a small-open economy in which rate of interest is given in global markets, while this study treats the rate of interest as an endogenous variable. This study carries out dynamic analysis with endogenous land value and residential location. The paper is organized as follows. Section 2 defines the spatial growth model with endogenous land value and residential location. Section 3 simulates the motion of the economic system. Section 4 carries out comparative dynamic analysis with regard to the total productivity of the production sector, transportation conditions, amenity, and preference. Section 5 concludes the study. The appendix proves the main results in section 3.
2. THE MODEL
En México según datos de la Encuesta Nacional de Ocupación y Empleo (ENOE) para el "primer trimestre del 2020 existen 6.5 millones de personas que se dedican al trabajo agrícola" (INEGI, 2020), este entendido como hombres y mujeres que siembran y cultivan el campo y cosechan sus productos, de estos 5.8 millones son hombres y 0.77 millones son mujeres, con un promedio de edad en el sector de 41.7 años y el promedio de escolaridad de esta población es de 5.9 años, lo que significa primaria incompleta (por debajo del promedio nacional de 8 años), de cada 100 trabajadores agrícolas, 24 hablan lengua indígena. We now build the model of dynamic interdependence between economic growth and residential density change over space by combining the basic features of the Solow growth model and the Alonso residential model with Zhang's approach to household behavior. We describe the residential land-use by following the Alonso model. The economic system is an isolated urban economy built on a flat featureless plain. All workers reside over the city and work in the CBD. People travel only between dwelling sites and the CBD. An individual reside only at one location. The only spatial characteristic that directly matters is the distance from the residential site to the CBD. The isolated state consists of a finite strip of land extending from a fixed central business district (CBD) with constant unitwidth. The system is geographically linear and consists of two parts - the CBD and the residential area. We use L to stand for the fixed (territory) length of the isolated state. We assume that all economic activities are concentrated in the CBD. Let ú) stand for the distance from the CBD to a point in the residential area. We use R(t,ü)) and p(t,ü)) to represent the land rent and land price at location ú) at time t. The households occupy the residential area. As we will get the same conclusions if we locate the CBD at the center of the linear system, the specified urban configuration will not affect our discussion. The system has one industrial sector. The industrial production is the same as that in the one-sector neoclassical growth model. We assume that the industrial product can be either invested or consumed. Housing is measured by lot size. The total labor force is fully employed by the industrial sector. We select industrial good to serve as numeraire. As we assume that the transportation cost of workers to the city is dependent on the travel distance, land rent for housing should be spatially different. We use K(t) to stand for the total capital stock.
The total labor input
We use n(t, ω) to denote the residential density at ω. We assume that all the workers work the same time, irrespective of where they live. The population N is homogenous and constant. In the literature of urban economics there are studies on urban structure with heterogeneous households (Beckman, 1969; Solow, 1973; Beckmann and Papageorgiou, 1989; Anas, 1990; Lucas and Rossi-Hansberg, 2002; Tabuchi and Thisse, 2002). The total labor force is the sum of the labor input over the space. The width of the urban area is assumed to be unity. According to the definition of n(t, ω), we have:
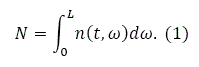
The production sector
Let F(t) stand for the production function. The production function is specified as follows:
![]()
where A, α, and β are positive parameters. The capital goods sector employs two input factors, capital and labor force. We assume that all the markets are perfectly competitive. Labor and capital earn their marginal products, and firms earn zero profits. The rate of interest r(t), and wage rate w(t), are determined by markets. Hence, for any individual firm r(t) and w(t) are given at each point in time. The production sector chooses capital K(t) and labor force N(t) to maximize its profit. The marginal conditions are given by:
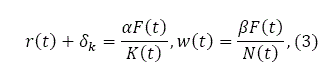
where δk is the depreciation rate of physical capital. We consider that wages are independent of where households live. Some studies suggest that wages should be related to distance from the residential site to urban centers (Muth, 1969; and White, 1976).
The relation between the lot size and residential density
We assume that all housing is residential. For simplicity we assume that housing is measured by lot size (Anas, 1978; Fischer et al. 1996; Arnott, 1980; Arnott et al. 1999; Lin et al., 2004; and Glaeser and Gyourko, 2005). Residential housing assets play a dual in the economy. First, residential housing assets are used as a durable consumption good. They are the source of housing services. Residential housing assets are used as a mechanism for the intertemporal transfer of wealth, which generates both rents and capital gains through housing appreciation. Let us denote l(t,ω) the lot size of the household at ω. According to the definitions of l and n, we have:
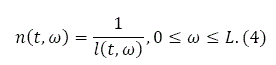
Choice between physical wealth and land
Consider now a household with one unity of money. He can either invest in capital good thereby earning a profit equal to the net own-rate of return r(t) or invest in land thereby earning a profit equal to the net own-rate of return R(t, ω)/p(t, ω). As we assume capital and land markets to be at competitive equilibrium at any point in time, the two options yield equal returns, i.e.
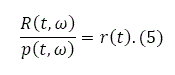
These equations enable us to determine portfolio equilibrium choice between land and (physical) wealth. It is easy to see that equations (5) are established under many strict conditions. For instance, we omit any transaction costs and any time delay for buying and selling. Equation (5) also implies perfect information. It should be noted that a relation similar to (5) is used in the long-term steady state analysis in literature of urban economics (Fujita, 1989). The land value p(ω, t) is equal to the present value of anticipated land rents:
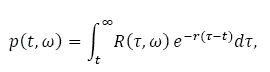
where r is the discount rate. If we assume that the land rent is invariant over time, then we have:
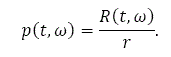
Travel time and cost to the CBD
All the land is only for residential use. As work time is exogenously fixed equally for all the residents, a resident decides the time distribution between leisure time and travel time. We assume that work time is exogenously fixed. It is assumed that the travel time from the CBD to the residential location is only related to the distance. We neglect any other effects such on technological change, infrastructure improvement, and congestion on the travel time form the CBD to the residential area. Let T0 and T(ω) respectively stand for the total available time and the time spent on traveling between the residence and CBD. We should require that the travel time increases in ω. We have:
![]()
where T(ω) is the leisure time that the household at ω enjoys. As the travel is fixed for a given distance, the leisure time is also dependent only on the location. In reality, economic activities such as retailing, goods production, services, green parks, and transportation use land. Solow and Vickery (1971), for instance, study urban land use for transportation in a similar spatial setting as in this study. At each location, land is distributed between transportation and housing as follows: LH(ω) + LT(ω) ≤ 1, where LH(ω) and LT(ω) are respectively the ratios of land devoted to housing and transportation. In order to extend out study, we refer to, for instance, Oron et al (1973) who study endogenous speed and congestion, and Yang and Huang (2005) who deal with pricing and congestions. There are different types of congestions and externalities (e.g., Anas and Kim, 1996; Arnott, 2007; Ahlfeldt et al. 2015; and Brinkman 2016).
This study assumes that the travel cost cT(ω, t) from location ω to the CBD is dependent on the distance as follows:
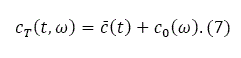
Transport mode is an endogenous variable, which implies that like housing, transportation service should enter the utility function. Transportation cost is related to income (e.g., Train and McFadden, 1978; Rietveld et al, 2003; and De Palma et al, 2005).
Land ownership, current income, and disposable income
As in many studies in urban economics (e.g., Zhang, 2002), we use lot size to stand for housing. As argued, for instance, by Davis and Heathcote (2007), most of the fluctuations in house prices are driven by land price rather than by the cost of structures. This implies that it is acceptable to use lot size to stand for housing when dealing with dynamics of housing value. Let k(ω , t) stand for the representative household's physical wealth, and a(ω, t) for the value of land owned by the household at location ω. The total value of land owned by the household at ω is the sum of all the value of land the household owns in the economy. We have
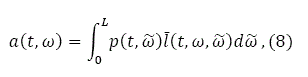
where l(t,ω, ![]() ) is the land that the household at ω owns at
) is the land that the household at ω owns at ![]() .
.
The total value of wealth v(t, ω) owned by the household at ω is the sum of the two assets' values
![]()
The household at ω collects the following rent from the land that the household owns:
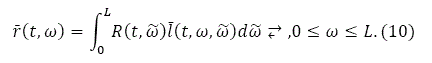
The total land rent of the economy is equal to the land rent that the population owns:

The household at ω has the following current income:
![]()
from the interest payment rk, and the wage payment w, and the land rent income ![]() . We call y(t,ω) the current income in the sense that it comes from consumers' wages and current earnings from ownership of wealth. The total value of the wealth that a consumer at location (jó can sell to purchase goods and to save is equal to a(t,ω). Here, we assume that selling and buyingwealth can be conducted instantaneously without any transaction cost. The disposable income
. We call y(t,ω) the current income in the sense that it comes from consumers' wages and current earnings from ownership of wealth. The total value of the wealth that a consumer at location (jó can sell to purchase goods and to save is equal to a(t,ω). Here, we assume that selling and buyingwealth can be conducted instantaneously without any transaction cost. The disposable income ![]() (t, ω) is then the sum of the current income and the total value of wealth. As we don't take account of possible borrowing, we have:
(t, ω) is then the sum of the current income and the total value of wealth. As we don't take account of possible borrowing, we have:
![]()
The disposable income is used for saving and consumption. At time t the consumer has the total amount of income equaling ![]() to distribute between consuming and saving.
to distribute between consuming and saving.
The budget
At each point in time, the household at location ú) distributes the total available budget between housing l(t,ω), saving s(t,ω), consumption of industrial goods c(t,ω), and travelling, cT(ω). The total expenditure is:
![]()
The disposable income equals the total expenditure, i.e.
![]()
Insert(11)and(10)in (12):
![]()
where
![]()
Utility, amenity and optimal solution
Consumers make decisions on choice of lot size, consumption level of commodity as well as on how much to save. This study uses the approach to consumers' behavior proposed by Zhang in the early 1990s (Zhang, 1993). This approach makes it possible to solve many national, international, urban, and interregional economic problems, such as growth problems with heterogeneous households, multi-sectors, and preference changes, which are analytically intractable by the traditional approaches in economics. It should also be remarked that in the growth literature, for instance, in the Solow model, the saving is out of the current income y while in this study the saving is out of the disposable income which is dependent both on the current income and wealth. We assume that utility level U(t,ω) of the household at location ω is dependent on T(ω), l(t,ω), s(t,ω), and c(t,ω) as follows:
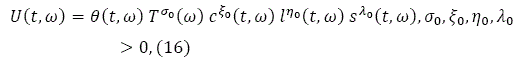
in which σ0, ξ0, no, and λo are a typical person's elasticity of utility with regard to leisure time, industrial goods, housing, and saving. We call σ0, ξ0, n0, and λo propensities to use leisure time, to consume goods, to consume housing, and to hold wealth, respectively.
In our approach distance from the CBD reflects two elements: the inconvenience of the distance and the value of the amenity of the surrounding area. The urban dynamics is influenced by many changing characteristics of environmental quality such as air quality, levels of noise pollution, open space, and other physical and social neighborhood qualities at each location. Environmental quality can be reflected in part by its effect on the location choice of the individual. Many kinds of externalities may exist at any location. Some may be historically given, such as historical buildings and climate; others such as noise and cleanness, may be endogenously determined by the location of residents. Households may prefer a low-density residential area to a high one, as there tend to have more green, less noise, more cleanness and more safety in a low-density area. Nevertheless, there are other factors, such as social interactions, which may make high-density area attractive. Glaeser et al (2001: 27) point out: "Most urban scholars think of cities as offering positive agglomeration benefits in the productive sphere, and as having negative agglomeration effects (or congestion effects) on non-work consumption". Their empirical study demonstrates that high amenity cities grown faster than low amenity cities and that the role of urban density in maintaining urban growth is important. In this study we assume that local amenity is dependent on local residential density. We specify the amenity θ(ω, t) at ω as follows:
![]()
The function θ(t,ω) implies that the amenity level at location ω is related to the residential density at the location. This specified form is a limited case. Locational amenities or disamenities are not only affected by the residential density at the location. For instance, possible social contacts of any individual are spread over the whole space. For instance, Hoehn et al. (1987) take account of a city-wide amenity in examining wages and prices. Air pollution is not limited to locals.
Maximizing U(ω,t) subject to the budget constraint (8) yields:
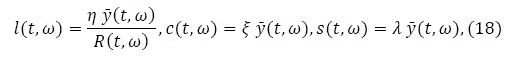
where
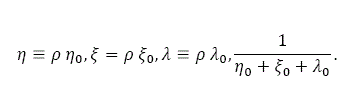
The above equations mean that the housing consumption, consumption of the good and saving are positively proportional to the potential available income.
Equal utility level over the residential area
To determine residential distribution, we require that all the households obtain the same level of utility at any point in time. This also comes out of our assumption that the population is homogeneous, and people can change their residential location freely without any transaction costs and time delay. The conditions that households get the same level of utility at any location at any point is represented by:
![]()
Here we neglect possible costs for migration.
Wealth accumulation
According to the definition of s(t,ω), the wealth accumulation of the household at location ω is given by:
![]()
The land market equilibrium
According to the definition the total value of the national land V(t) is:
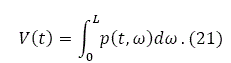
The total value of land owned by the population is given by:
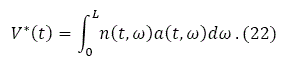
As the land is privately owned, the two values should equal:
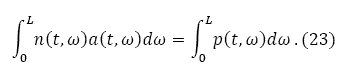
The equilibrium for good production and consumption
The total consumption C(t) is given by:
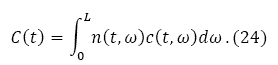
Change in physical capital is the national production minus the national consumption and physical depreciation. We have:
![]()
All the capital being owned by the population
The total capital stock employed by the production sector is equal to the total wealth owned by all the households. That is:

We have thus built the dynamic growth model with endogenous spatial distribution of wealth, time, consumption and population, capital accumulation and residential location. From the construction process we see that if we neglect space in our model, the model is similar to the Solow growth model. If we omit wealth accumulation and capital accumulation, the model is similar to the Alonso model. We now examine dynamic properties of the system.
3. THE SPATIAL DYNAMICS
The previous section defines the model with residential structure by integrating the basic ideas in Solow's growth and Alonso's residential models with Zhang's alternative approach to household behavior. This section examines properties of the spatial model. The following lemma provides a computational procedure to plot the motion of the economic system.
Lemma
Assume ![]() , where
, where ![]() is a constant. The dynamics of capital stock and the wealth per household, K(t) and v(t), are described by the following two differential equations:
is a constant. The dynamics of capital stock and the wealth per household, K(t) and v(t), are described by the following two differential equations:
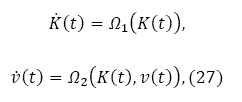
in which Ω1 and Ω2 are functions of K(t) and v(t) defined in the appendix. For given K(t) and v(t), we uniquely determine all the other variables by the following procedure:![]() by
by
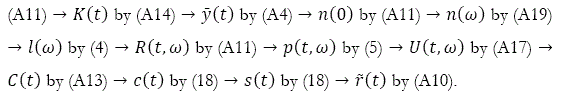
In the lemma ![]() is the total wealth defined by:
is the total wealth defined by:
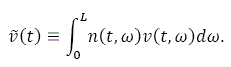
We specify the parameters as follows:
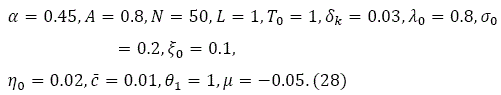
The population is fixed at 50 units and the urban length is fixed at one unit. The total available time for enjoying leisure and commuting is unit. The total factor productivity is specified with 0.8. We specify α with 0.45. These specifications will not affect our results with regards to comparative dynamic analysis. We assume that the commuting cost is only dependent on the wage and independent of the distance. As shown in the appendix this strict assumption is made only for simplicity of deriving the differential equations. The specified value of CT implies that one percent of the wage is spent on commuting. The impact of distance on the city structure in the rest of the paper is due to the distance-related amenity and commuting time. The propensities to consume goods and consume housing are respectively specified at 0.1 and 0.02, which implies that the expenditures on goods is 5 times as the expenditure on housing. The propensity to use leisure is specified at 0.2. The amenity parameter, µ, is negative. This implies that with all the other conditions equal the household prefers to living in an area with low residential density. We fix the depreciation rate at 0.05.
We specify the following initial conditions:
![]()
Under (28) we plot the variables over time and space in in Figure 1. The national capital stock and national total wealth fall. The total wealth per household rises over time. The total output falls. The wage rate falls, and the rate of interest rises. The household consumes more. The residential density falls, and lot size rises in distance to the CBD. The amenity rises and leisure time falls in distance to the CBD. The land value and rent rise over time at any location and fall in distance at any time.
4. COMPARATIVE DYNAMIC ANALYSIS
The previous sector studies the equilibrium structure of the economic geography. First, we examine effects of change in the total productivity. We introduce a symbol Δx to stand for the change rate of the variable X in percentage due to changes in value of a parameter value.
A rise in the total factor productivity
We now allow the total factor productivity to be changed as follows: A0:0.8 => 0.81. There are no changes in the residential density, the lot size, the amenity, and leisure time as
![]()
The simulation results on the other variables are plotted in Figure 2. As the productivity is improved, the rate of interest is reduced. The total capital stock, wealth per household, the total output, the wage rate and consumption level per household are increased. The land value and rent are increased over time and space.
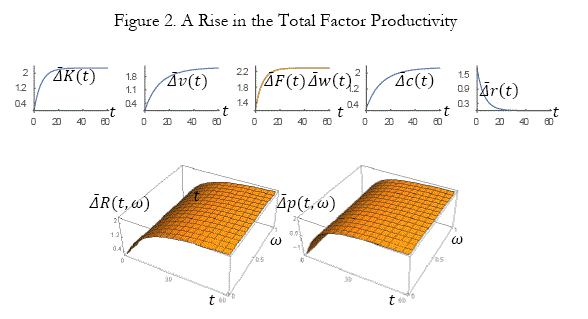
A rise in the propensity to save
We now examine what happen to the economic system when the propensity to save is changed as follows: λ0 0.8 => 0.81. There are no changes in the residential density, the lot size, the amenity, and leisure time. The simulation results on the other variables are plotted in Figure 3. As the propensity to save is improved, the rate of interest is reduced. The total capital stock, wealth per household, the total output, the wage rate and consumption level per household are increased. The land value and rent are increased over time and space.
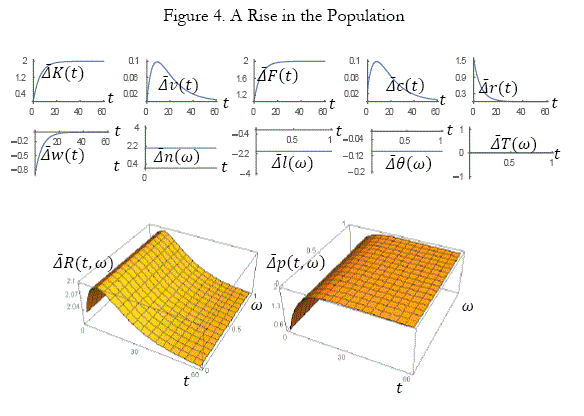
A rise in the population
We now examine what happen to the economic system when the population is increased as follows: N0: 50 => 51. The simulation results are plotted in Figure 3. The residential density is increased. The lot size and the amenity are reduced at any location. The leisure time is noted affected. The national wealth and output are increased. The total wealth per household is increased. The rate of interest is increased initially and is not affected in the long term. The wage rate is initially reduced and is not affected in the long term. The land value and rent are increased over time and space.
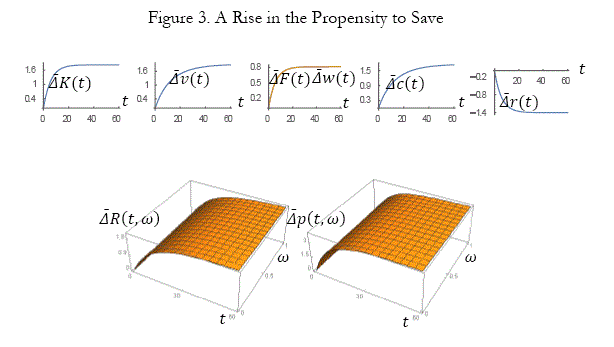
A rise in the propensity to enjoy leisure
We now examine what happen to the economic system when the propensity to enjoy leisure is increased as follows: σ0: 0.2 => 0.3. The simulation results are plotted in Figure 5. The lot size and the amenity are reduced near the CBD and are increased far away from the CBD. The residential area becomes denser near the CBD and less dense far away from the CBD as a consequence that people enhance their preference for lot size. The land value and rent are increased near the CBD are increased and the variables are reduced far away from the CBD.
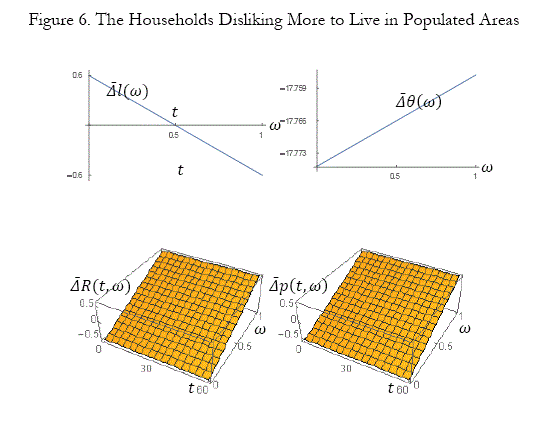
The household disliking more to live in populated areas
We now allow the parameter in the amenity function to be decreased as follows: µ: 0.05 => 0.1. The simulation results are plotted in Figure 6. The lot size is increased near the CBD and reduced far away from the CBD. The amenity is reduced over space. The land value and rent are reduced near the CBD and are increased far away from the CBD. The other variables are not affected.
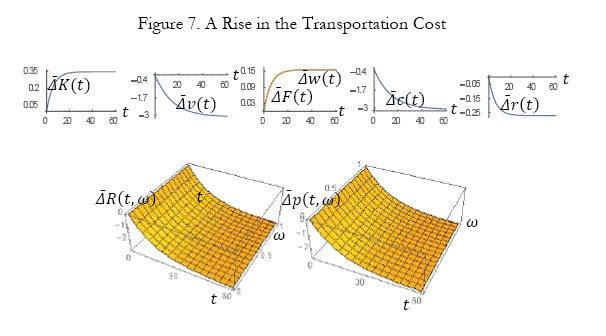
A rise in the transportation cost
We now examine what happen to the economic system when the transportation cost is increased as follows: CT 0.01 => 0.04. The simulation results are plotted in Figure 7. The lot size, the amenity and leisure time are not affected. The national physical capital and output level are enhanced. The wage rate is increased. The total wealth and consumption level per household are reduced. The rate of interest is reduced. The land value and rent are reduced over time and space.
5. CONCLUDING REMARKS
This study dealt with economic growth and residential distribution by integrating the Solow growth and Alonso residential distribution model. A unique feature of the study is to endogenously determine land value and rent with interactions between wealth accumulation, amenity, land, and transportation conditions. We built a spatial growth model in which the economic production and growth mechanism are based on the Solow growth model, the residential distribution is based on the Alonso model, the land price is based on Zhang's recent work on economic growth with endogenous land value, and the transportation conditions are exogenous. The economy is isolated and developed along a straight line with unit width. We simulated the motion of the spatial economy over time and space. We also carried out comparative dynamic analysis with regards to the total productivity of the industrial sector, transportation conditions, amenity, and preference on the spatial dynamics. As capital accumulation, residential location and land value are endogenous our study makes it possible to introduce dynamics among transportation systems, land value and rent, economic growth. Although the model is developed with microeconomic foundation and deals with complicated interactions among many variables over time and space, it is based on many strict assumptions. For instance, the travelling cost is not dependent on the distance and we neglect possible congestions. We also neglect inner complexity of the CBD. We have a single type of residents. Economic structure is also oversimplified. It is well-observed that households of different incomes locate their dwellings in different locations. It is possible for us to incorporate multiple income groups within our framework, even though this might cause new analytical difficulties. Many other limitations of the model become apparent in the light of the sophistication of the literature of economic growth theory, regional science and urban economics. Nevertheless, the model makes a unique contribution in the sense that it synthesizes the main ideas in neoclassical growth theory and neoclassical urban economics.
Appendix
From (2) and (3), we have:
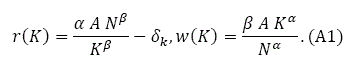
We omit time variable in expressions, except when it is necessary. Insert (8) and the definition of f (ω) in the definition of y:
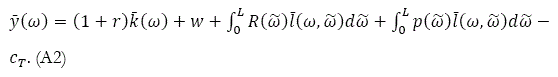
Insert (5) in (A2)

Insert (8) and (9) in (A3)
![]()
From (18) and (A5), we have:
![]()
Insert (4) in (A5)
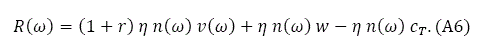
Integrate (A4) from 0 to L:
![]()
where we use (11) and
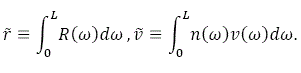
From the definitions of V we have:
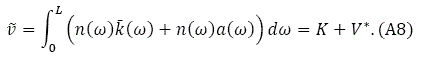
From (5) we have
![]()
From (8) and (9) we have:
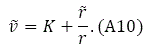
From (A7) and (A10) we solve:
![]()
where
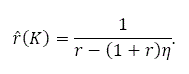
From (18) and (A4), we have:
![]()
Multiplying the two sides of (A10) by n and then integrate the resulted equation from 0 to L:
![]()
Insert(A11)in(23):
![]()
As the right-hand side of (A14) contains a single variable, we can solve the equation. In the rest of the appendix we treat K(t) as known.
Insert (18) and (A4) in (20):
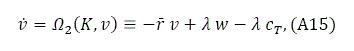
where
![]()
This is a first-order linear differential equation with non-constant coefficients. Its general solution is given by:
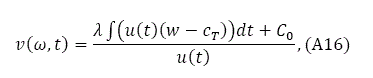
where C0 is a constant to be determined and
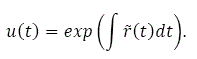
Hence, in the rest of the appendix we treat K(t) and v(ω, t) as known functions of time. Insert (17), (18) and (4) in (16)
![]()
where ![]() Insert (A17) in (19)
Insert (A17) in (19)
![]()
where
![]()
From (A18) we solve
![]()
where
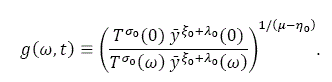
Insert (A19) in (1)
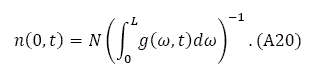
We can now determine all the variables over time and space by the procedure in the lemma.
REFERENCES
Agell, J. and Edin, P.A. (1990) Marginal Taxes and the Asset Portfolios of Swedish Households. The Scandinavian Journal of Economics 92 (1), 47-64. [ Links ]
Ahlfeldt, G., Redding, S.J., Sturm, D., and Wolf, N. (2015) The Economics of Density: Evidence from the Berlin Wall. Econometrica 83(6), 2127-89. [ Links ]
Albouy, D. and Lue, B. (2015) Driving to Opportunity: Local Rents, Wages, Commuting, and Sub-Metropolitan Quality of Life. Journal of Urban Economics 89, 74-92. [ Links ]
Alonso, W. (1964) Location and Land Use. MA., Cambridge: Harvard University Press. [ Links ]
Anas, A. (1978) Dynamics of Urban Residential Growth. Journal of Urban Economics 5, 66-87. [ Links ]
Anas, A. (1990) Taste Heterogeneity and Urban Spatial Structure: The Logit Model and Monocentric Theory Reconciled. Journal of Urban Economics 28, 318-35. [ Links ]
Anas, A. and Kim, I. (1996) General Equilibrium Models of Polycentric Urban Land Use with Endogenous and Job Agglomeration. Journal of Urban Economics 40(2), 232-56. [ Links ]
Arnott, R.J. (1980) A Simple Urban Growth Model with Durable Housing. Regional Science and Urban Economics 10, 53-76. [ Links ]
Arnott, R., Braid, R., Davidson, R. and Pines, D. (1999) A General Equilibrium Spatial Model of Housing Quality and Quantity. Regional Science and Urban Economics 29, 283-316. [ Links ]
Arnott, F. (2007) Congestion Tolling with Agglomeration Externalities. Journal of Urban Economics 62(2), 187-203. [ Links ]
Beckmann, M.J. (1969) On the Distribution of Urban Rent and Residential Density. Journal of Economic Theory 1, 60-7. [ Links ]
Beckmann, M.J. and Papageorgiou, Y.Y. (1989) Heterogeneous Tastes and Residential Location. Journal of Regional Science 29, 317-23. [ Links ]
Beeson, P. and Eberts, R.W. (1989) Identifying Productivity and Amenity Effects in Interurban Wage Differentials. The Review of Economics and Statistics 71, 443-52. [ Links ]
Brinkman, J.C. (2016) Congestion, Agglomeration, and the Structure of Cities. Journal of Urban Economics 94, 13-31. [ Links ]
Brito, P.M.B. and Pereira, A.M. (2002) Housing and Endogenous Long-Term Growth. Journal of Urban Economics 51, 246-71. [ Links ]
Brueckner, J.K. (1987) The Structure of Urban Equilibria: A Unified Treatment of the Muth-Mills Model. Mills, E.S. (Ed.) Handbook of Regional and Urban Economics, vol. 2. Amsterdam: Elsevier. [ Links ]
Burmeister, E. and Dobell, A.R. (1970) Mathematical Theories of Economic Growth. London: Collier Macmillan Publishers. [ Links ]
Capello, R. and Nijkamp, P. (2004, edited) Urban Dynamics and Growth: Advances in Urban Economics. Amsterdam: Elsevier. [ Links ]
Chen, Y. and Rosenthal, S. (2008) Local Amenities and Life-Cycle Migration: Do People Move for Jobs or Fun? Journal of Urban Economics 64, 519-37. [ Links ]
Cobb-Clark, D. and Hilderbrand, V.A. (2009) The Asset Portfolios of Native-born and Foreign-born Australian Households. Economic Record 85 (268), 46-59. [ Links ]
Davis, M. A., and Heathcote, J. (2007) The Price and Quantity of Residential Land in the United States, Journal of Monetary Economics 54, 2595 620. [ Links ]
De Palma, A., Kilani, M. and Lindsey, R. (2005) Congestion Pricing on a Road Network: A Study Using the Dynamic Equilibrium Simulator METROPOLIS. Transportation Research A 39, 588-611. [ Links ]
Fischer, M.M., Button, K.J. and Nijkamp, P. (1996, edited) Regional Housing and Labour Markets. Cheltenham: Edward Elgar. [ Links ]
Fujita, M. (1989) Urban Economic Theory Land Use and City Size. Cambridge: Cambridge University Press. [ Links ]
Gabriel, S.A., Mattey, J.P., and Wascher, W.L. (2003) Compensating Differentials and Evolution in the Qaulity-of-Life Among US states. Regional Science and Urban Economics 33, 619-49. [ Links ]
Gaudecker, H. von. (2015) How Does Household Portfolio Diversification Vary with Financial Literacy and Financial Advice? The Journal of Finance 70 (2), 489-507. [ Links ]
Glaeser, E.L. and Gyourko, J. (2005) Urban Decline and Durable Housing. Journal of Political Economy 113, 345-75. [ Links ]
Glaeser, E.L., Kolko, J., and Saiz, A. (2001) Consumer City. Journal of Economic Geography 1, 27-50. [ Links ]
Guiso, L., Haliassos, M., and Jappelli, T. (2002) Household Portfolios. Mass., Boston: MIT Press. [ Links ]
Henderson, J.V. (1985) Economic Theories and Cities. New York: Academic Press. [ Links ]
Henderson, J.V. andThisse,J.F. (2004, ed.) Handbook of Regional and Urban Economics. Amsterdam: Elsevier. [ Links ]
Hoehn, J.P., Berger, M.C., and Blomquist, G.C. (1987) A Hedonic Model of Interregional Wages, Rents and Amenity Values. Journal of Regional Science 27, 605-20. [ Links ]
Leung, C.K.Y. and Teo, W.L. (2011) Should the Optimal Portfolio Be Region-Specific? A Multi-region Model with Monetary Policy and Asset Price Co-Movements. Regional Science and Urban Economics 41(3), 293-304. [ Links ]
Lin, C.C., Mai, C.C. and Wang, P. (2004) Urban Land Policy and Hosing in an Endogenously Growing Monocentric City. Regional Science and Urban Economics 34, 241-61. [ Links ]
Liu, Z; Wang, P.F., and Zha, T. (2011) Land-Price Dynamics and Macroeconomic Fluctuations. Working Paper, Federal Reserve Bank of Atlanta, No. 2011-11. [ Links ]
Lucas, R.E. (1988) On the Mechanics of Economic Development. Journal of Monetary Economics 22, 3-42. [ Links ]
Lucas, R.E. and Rossi-Hansberg, E. (2002) On the Internal Structure of Cities. Econometrica 70(4), 1445-76. [ Links ]
Mills, E.S. (1967) An Aggregative Model of Resource Allocation in Metropolitan Areas. American Economic Review 57, 197-210. [ Links ]
Muth, R.F. (1969) Cities and Housing. Chicago: University of Chicago Press. [ Links ]
Oates, W.E. (1969) The Effects of Property Taxes and Local Public Spending on Property Values: An Empirical Syudy of Tax Capitalization and the Tiebout Hypothesis. Journal of Political Economy 77, 957-71. [ Links ]
Oron, Y., Pines, D. and Sheshinski, E. (1973) Optimum vs Equilibrium Land Use Pattern and Congestion Toll. Bell Journal of Economics and Management Science 4, 619-36. [ Links ]
Rabenau, B.V. (1979) Urban Growth with Agglomeration Economics and Diseconomics. Geographia Polonica 42, 77-90. [ Links ]
Richardson, B.V. (1973) Regional Growth Theory. New York: John Wiley. [ Links ]
Rietveld, P., Button, K. and Nijkamp, P. (2003, edited) Urban Transport. Cheltenham: Edward Elgar. [ Links ]
Roback, J. (1982) Wages, Rents, and the Quality of Life. Journal of Political Economy 90, 1257-78. [ Links ]
Rosen, S. (1979) Wages Based Indexes of Urban Quality of Life. Straszheim, M. and Mieszhowski, M. (Eds.) Current Issues in Urban Economics, Baltimore: John Hopkins University Press. [ Links ]
Sato, Y.H. and Xiao, W. (2015) Land Development, Search Frictions and City Structure. Regional Science and Urban Economics 50, 63-76. [ Links ]
Solow, R. (1956) A Contribution to the Theory of Growth. Quarterly Journal of Economics 70, 65-94. [ Links ]
Solow, R.M. (1973) On Equilibrium Models of Urban Location, in Essays in Modern Economics, edited by Parkin, M. London: Longman. [ Links ]
Solow, R.M. and Vickrey, W.S. (1971) Land Use in a Long Narrow City. Journal of Economic Theory 3, 430-47. [ Links ]
Swan, T.W. (1956) Economic Growth and Capital Accumulation. Economic Record 32, 334-61. [ Links ]
Tabuchi, T. and Thisse, J.F. (2002) Taste Heterogeneity, Labor Mobility and Economic Geography. Journal of Development Economics 69,155-77. [ Links ]
Tiebout, C.M. (1956) A Pure Theory of Local Expenditures. Journal of Political Economy 64, 416-24. [ Links ]
Train, K. and McFadden, D. (1978) The Goods/Leisure Tradeoff and Disaggregate Work Trip Mode Choice Models. Transportation Research 12, 349-53. [ Links ]
Uhler, R.S. and Gragg, J.G. (1971) The Structure of the Asset Portfolios of Households. The Review of Economic Studies 38 (3), 341-57. [ Links ]
White, M. (1976) Firm Suburbanization and Urban Subcenters. Journal of Urban Economics 3, 323-43. [ Links ]
Yang, H. and Huang, H.J. (2005) Mathematical and Economic Theory of Road Pricing. Amsterdam: Elsevier Science. [ Links ]
Zhang, W.B. (1993) Woman's Labor Participation and Economic Growth -Creativity, Knowledge Utilization and Family Preference. Economics Letters 42, 105-110. [ Links ]
Zhang, W.B. (1993a) Wages, Service Prices and Rent - Urban Division of Labor and Amenities. Seoul Journal of Economics 6, 97-113. [ Links ]
Zhang, W.B. (2002) An Economic Theory of Cities - Spatial Models with Capital, Knowledge, and Structures. Berlin: Springer. [ Links ]
Zhang, W.B. (2008) Growth and Residential Distribution with Economic [ Links ]
Structure and Amenity: A Synthesis of Solow-Uzawa's Growth,
Alonso's Urban, and Muth's Housing Models. Papers in Regional Science 87, 277-303. [ Links ]
Zhang, W.B. (2016) Gold and Land Prices with Capital Accumulation in an Economy with Industrial and Agricultural Sectors. Annals - Economy Series; Constantin Brancusi University 2016(2), 16-29. [ Links ]
Zhang, W.B. (2018) Growth, Residential Distribution and Endogenous Land Value in an Integrated Solow's Growth and Alonso's Residential Model. Asian Themes in Social Sciences Research 2(1), 23-31. [ Links ]