Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Revista CON-CIENCIA
Print version ISSN 2310-0265
Rev.Cs.Farm. y Bioq vol.4 no.1 La Paz June 2016
ARTÍCULOS DE INVESTIGACIÓN
Oscilador armónico cuántico: la energía vibracional en las moléculas
CASTAÑETA, HERIBERTO1
NOGALES, JORGE 2
CORRESPONDENCIA: JORGE.NOGALES.VERA@GMAIL.COM
1Carrera de Ciencias Químicas. FCPN-UMSA Cota Cota calle 27 Campus Universitario La Paz - Bolivia
2Química General e Inorgánica,carrera Química Farmacéutica. FCFB-UMSA. Av. Saavedra 2224 La Paz - Bolivia
FECHA DE RECEPCIÓN: 18/02/2016 FECHA DE ACEPTACIÓN: 11/05/2016
Resumen
En esta revisión se deduce la energía de la vibración en las moléculas químicas según el modelo del oscilador armónico , se resuelve la ecuación de Schrodinger independiente del tiempo para el oscilador armónico cuántico utilizando para tal efecto una solución en series de potencias de la variable en forma detallada . Es importante hacer notar que los osciladores cuánticos no pueden tener energía cero , con las moléculas ocurre lo mismo estas no pueden tener energía de vibración cero, siendo su energía mínima hv/2 .Esta energía origina la vibración del enlace incluso a 0 K . La mayoría de las moléculas no poseen energía suficiente para situarse en estados excitados de vibración , si pueden excitarse mediante absorción de radiación de energía E1-Eo = hv, este fenómeno es el origen de los espectros de vibración o espectros infrarrojos IR; es decir los espectros de IR surgen a consecuencia de la variación discontinua de la energía de vibración de una molécula debido a la absorción de radiación .
Palabras Clave
Oscilador, vibración, Schrodinger, , infrarrojo
Abstract
In this review the energy of vibration follows on the chemical molecules modeled harmonic oscillator, Schrodinger 's equation is solved independent of time for the quantum harmonic oscillator using a solution in power series variable in detail. Ifs important to note that quantum oscillators cannot have zero energy, the same happens with the molecules they can't they cannot have zero energy vibration, its minimum energy being hv / 2. This energy causes the vibration of the link even at 0 K. Most molecules have no sufficient energy to stand in excit-ed vibrational states, they can be excited by absorption of radiation energy E1 -Eo = hv , this phenomenon is the source of vibration spectra or spectra IR. That is, the IR spectra arise as a result of the discontinuous varia-tion of the vibrational energy of a molecule due to absorption of radiation
Key Words
Oscillator, vibration, Schrodinger, infrared.
Los enlaces químicos en las moléculas no son rígidos al contrario están constantemente oscilando respecto a cierta posición de equilibrio . El oscilador armónico cuántico explica la energía de vibración en las moléculas cuando las oscilaciones del enlace son pequeñas lo que sucede a temperatura ambiente o si adicionamos energía a la molécula en forma de calor la oscilación aumenta. El modelo del oscilador armónico explica las oscilaciones o vibraciones de los enlaces químicos , desde el punto de vista químico esta vibración explica la existencia de los espectros de vibración o infrarrojo (Ball W. D. ,2004:.283) .
Un oscilador armónico se rige por la ley de Hooke según la cual la fuerza es F= - Kx = - dV / dx, donde k es una constante y V la energía potencial. Integrando esta expresión se obtiene ![]()
La frecuencia v de un oscilador es ![]()
siendo m la masa . esta es la frecuencia fundamental de vibración y es una magnitud característica de cada enlace .
En esta revisión se deduce la energía de la vibración según el modelo del oscilador armónico cuántico utilizando series de potencia de la variable matemática en busca de la solución de la ecuación diferencial de Schrodinger para el oscilador armónico cuántico.
OSCILADOR ARMÓNICO CLÁSICO
El oscilador armónico clásico constituye un movimiento repetitivo , en el que una masa se desplaza de un lugar a otro en un movimiento que obedece la ley de Hooke. Dada una masa m, la ley de Hooke establece que en el caso de un desplazamiento x unidimensional a partir de una posición de equilibrio, la fuerza F que actúa en contra del desplazamiento (es decir, la fuerza que actúa para restituir la masa punto de equilibrio) es proporcional al desplazamiento:
F = -kx
donde k recibe el nombre de constante de fuerza. Obsérvese que tanto F como x son vectores y que el signo negativo en la ecuación indica que los vectores de fuerza y desplazamiento poseen sentidos opuestos. Como la fuerza se expresa en unidades comunes de newtons o dinas, y el desplazamiento en unidades de distancia, la constante de fuerza se expresa en unidades de N/m o en unidades que facilitan a veces la manipulación numérica. (Atkins, P. ,2008: 280)
La energía potencial, V, de un oscilador armónico que se rige por la ley de Hooke se relaciona con la fuerza mediante una integral simple. La relación y resultado final son
![]()
Para simplificar nuestra presentación, ignoraremos la característica vectorial de la posición y nos concentraremos en su magnitud, x. Puesto que x se encuentra elevada al cuadrado en la expresión de V, los valores negativos de x no necesitan considerarse de alguna forma particular. La ecuación que resulta después de los cálculos para la energía potencial de un oscilador armónico se expresa de forma simplificada de la siguiente manera:
![]()
La energía potencial no depende de la masa del oscilador. Desde una perspectiva clásica, se conoce bien el comportamiento del oscilador armónico.
Al oscilador le toma determinado tiempo, T, en segundos, efectuar un ciclo completo. Por lo tanto, en 1 segundo, habrá 1/T oscilaciones. En un movimiento sinusoidal, un ciclo corresponde a un cambio angular de 2π. La frecuencia del oscilador en número de ciclos por segundo o simplemente 1/ segundo (s-1); otro nombre aceptado para (s-1) es el de hertz o Hz) se define como v (letra griega nu) y es igual a
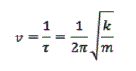
La frecuencia v es independiente del desplazamiento. Dichas relaciones se conocen desde el siglo XVII. Los osciladores armónicos familiares incluyen masas sobre resortes y péndulos de reloj. (Atkins, P. ,2008: 279)
Oscilador armónico cuántico
Desde el punto de vista de la mecánica cuántica, una función de onda para un oscilador armónico simple en una dimensión puede determinarse mediante la ecuación (independiente del tiempo) de Schrödinger:
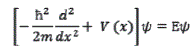
La energía potencial del sistema mecánico-cuántico posee la misma expresión de la energía potencial del sistema clásico. (En general, las energías potenciales son energías de posición, la forma de la energía potencial en mecánica cuántica es la misma que la expresión clásica. No obstante, como consecuencia de la forma de la ecuación de Schrödinger, el operador de la energía potencial se multiplica por la función de onda .La ecuación de Schrödinger para el oscilador armónico es
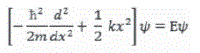
y las funciones de onda aceptables para este sistema en una dimensión deben satisfacer esta ecuación de eigenvalores. (Porta A ,1987 : 500 )
Esta ecuación diferencial posee una solución analítica. El método que aplicamos corresponde a una técnica general de solución de ecuaciones diferenciales: definimos la función de onda como una serie de potencias. Finalmente encontramos que, para resolver la ecuación de Schrödinger la serie de potencias debe poseer una forma especial.
Primero, reescribiremos la ecuación de Schrödinger para el oscilador armónico mediante la ecuación de la frecuencia del oscilador ![]()
elevando al cuadrado y despejando k., encontramos que la constante de fuerza k es: k = 4π2v2m
así, la ecuación de Schrödinger para un oscilador armónico simple en una dimensión corresponde a:
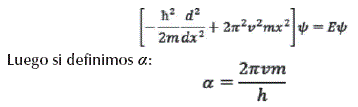
Segundo, multipliquemos ambos miembros de la ecuación por el término![]() . La ecuación de Schrödinger se convierte en:
. La ecuación de Schrödinger se convierte en:
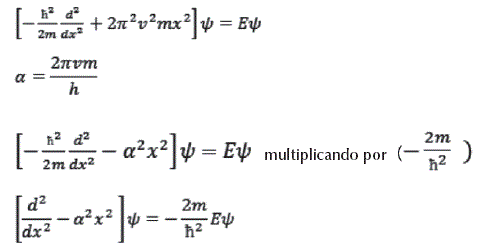
transponiendo los términos a uno de los miembros de la ecuación para obtener una expresión igual a cero :
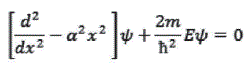
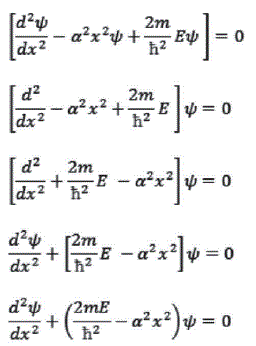
donde la ecuación se ha reordenado a partir de la expresión anterior para que aparezcan entre paréntesis los dos términos que sencillamente se están multiplicando por ![]() . El primer término es la segunda derivada de
. El primer término es la segunda derivada de ![]() .
.
Ahora según Ball (2004:300) supongamos que la forma de la función de onda y/ que satisface esta ecuación de Schrödinger posee la forma de una serie de potencias de la variable x. Es decir, la función de onda es una función f(x) que incluye la suma de un término que contiene a x° (el cual sencillamente es igual a 1), un término que contiene a x2 un término que contiene a x2, y así ad infinitum. Cada potencia de x posee una constante denominada coeficiente que la multiplica; así, la forma de f(x) (sabiendo que x°=1) es:
![]()
Las c son los coeficientes multiplicados por las potencias de x. Resulta más conciso expresar la función anterior con la notación convencional para la suma, como sigue:
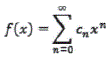
donde n es el índice de la sumatoria. En este caso, la suma tiende a infinito. Este hecho provoca un problema potencial, ya que las sumas que tienden a un número infinito de términos muchas veces se aproximan a infinito a menos que haya alguna forma de lograr que sea sucesivamente más pequeño. Una solución parcial consiste en suponer que cada término de la suma se multiplica por otro término que es mucho más pequeño que la x misma (y, por lo tanto, xn). El término que incluiremos en este proceso es eax2/2. (Observe la inclusión de la constante a). Esta función exponencial constituye un ejemplo de función gaussiana (denominada así en honor del matemático del siglo XIX Karl Friedrich Gauss). En estas condiciones, la función de onda de este sistema es
![]()
donde /(x) corresponde a la serie de potencias .
Ahora es posible calcular la primera y la segunda derivadas con respecto a x. Después se sustituyen las expresiones de la segunda derivada, así como la función original en la forma adecuada de la ecuación de Schrödinger. Al hacerlo, la lógica detrás de la elección de la función exponencial e-ax2/2fxse hará matemáticamente evidente. De acuerdo con la regla para la diferenciación de un producto, la primera derivada es:

Reemplazando la segunda derivada en la ecuación de Schrodinger para el oscilador armónico , tenemos :
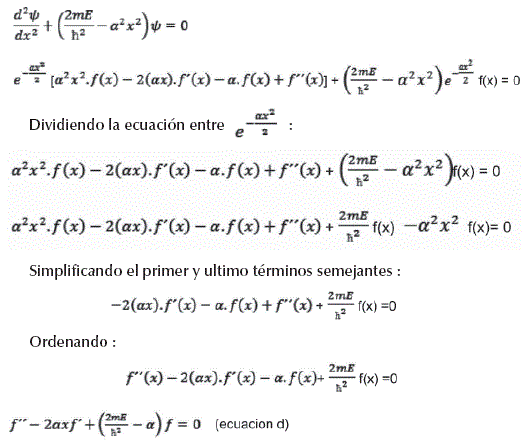
Esta ecuación cuenta con términos que se originan de la serie de potencias f, de su primera derivada f y de su segunda derivada ![]() Se han cancelado los términos en
Se han cancelado los términos en ![]() Como suponemos que f es una serie de potencias, en realidad podemos especifícar las derivadas término a término. Resolviendo la primera serie de potencias original, las derivadas son :
Como suponemos que f es una serie de potencias, en realidad podemos especifícar las derivadas término a término. Resolviendo la primera serie de potencias original, las derivadas son :
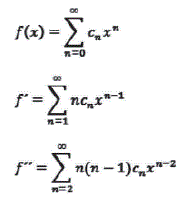
La derivación no influye en las cn puesto que son constantes. El valor inicial del índice n cambia para cada derivada. En la primera derivada perdemos el término n= 0 en virtud de que el término de la función original es constante.
Ahora, el término n = 1 es una constante ya que la potencia de x para n =1 es 0 , es decir, x1-1 = x= 1. (Pogosyan G. S., 2005 :19).
En la segunda derivada, el término n = 1, el cual es constante en el desarrollo de f, se vuelve cero en la segunda derivada, por lo que la suma para ![]() comienza con n=2.
comienza con n=2.
Puesto que el primer término de la sumatoria para se hace igual a 0 en f',esta primera derivada no cambia si añadimos un 0 como primer término y enseguida comenzamos la suma en n = 0. Entendamos que esto no cambia a f, ya que el primer término, n=0, equivale simplemente a 0. Ahora bien, esto nos permite comenzar la suma en n = 0 en lugar de n = 1. Por lo tanto, podemos escribir de la siguiente manera
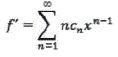
De nuevo, esto no altera la serie de potencias, sólo cambia el valor inicial del índice n. Se puede aplicar la misma técnica a ![]() . Puesto que el índice n es sencillamente un número para contar e identificar los términos en una serie de potencias, podemos desplazar simplemente el índice redefiniendo, digamos, un índice i como i = n - 2. Dado que esto significa que n = i + 2, la expresión de i segunda derivada
. Puesto que el índice n es sencillamente un número para contar e identificar los términos en una serie de potencias, podemos desplazar simplemente el índice redefiniendo, digamos, un índice i como i = n - 2. Dado que esto significa que n = i + 2, la expresión de i segunda derivada ![]() puede reescribirse llevando a cabo una sustitución para cada n :
puede reescribirse llevando a cabo una sustitución para cada n :
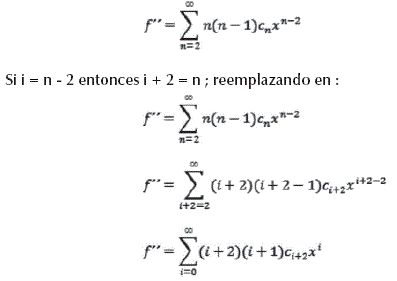
Matemáticamente, la función ![]() no ha cambiado. Lo que ha cambiado, es el índice, que se ha desplazado 2 lugares. Esta función corresponde a la misma segunda derivada que se calculó originalmente.( Quintero Zuluaga J.J.,2002 : 60 )
no ha cambiado. Lo que ha cambiado, es el índice, que se ha desplazado 2 lugares. Esta función corresponde a la misma segunda derivada que se calculó originalmente.( Quintero Zuluaga J.J.,2002 : 60 )
Por supuesto, no importa la letra que se emplee para designar el índice. Si éste es el caso, ¿por qué no utilizar n ?. Entonces la segunda derivada f" es
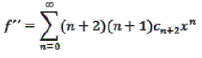
Reemplazando sumatorias para f(x) f '(x) y f " (x) en la (ecuación d)
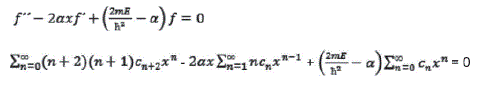
Como todas las sumatorias en la ecuación anterior comienzan en 0, se vuelven infinitas y emplean el mismo índice, se pueden reescribir como una sola suma y, por esa razón, se igualan los índices en todas ellas. (Arrieta1 A., 2009:518).
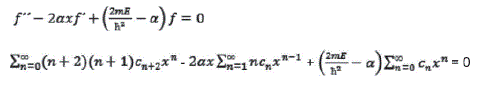
Esta ecuación se simplifica si tomamos en cuenta que es posible combinar las x en el segundo término de tal manera que la potencia de x sea n, y además, considerando que los tres términos incluyen la x elevada a la potencia n( xn = x° = 1 ). Si llevamos a cabo esta operación y factorizamos xn, obtenemos :
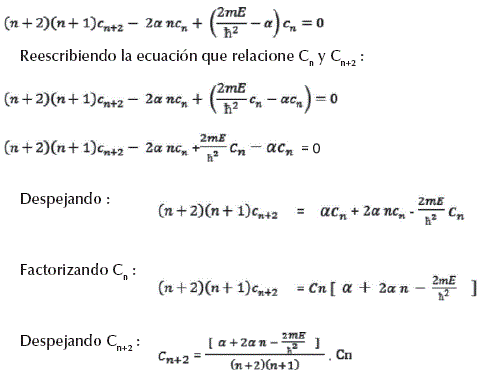
Una ecuación que relaciona coeficientes en sucesión, como la que se está considerando, recibe el nombre de fórmula de recursión y nos permite determinar coeficientes sucesivos si se conocen los anteriores. En última estancia, sólo se requiere conocer dos constantes de entrada: con la cual se determinan los coeficientes de potencia par c2, c4, c6,...y cn, a partir de la cual se encuentran los coeficientes de potencia impar c1, c3, C5,...y cn
Luego de esto según García Barneto, (2008: 680) es factible aplicar uno de los requisitos para las funciones de ondas aceptables: deben estar acotadas. Aunque la deducción que nos ocupa comenzó suponiendo una serie infinita como solución, la función de onda no puede ser infinita e incluso aplicarse a la realidad. Además, la inclusión del término e-ax2/2 no garantiza que la suma infinita esté acotada. Sin embargo, la fórmula de recursión proporciona una forma de garantizar esto. Puesto que el coeficiente Cn+2 depende de Cn si para algún n el coeficiente Cn es exactamente igual a cero, también son cero todas las constantes sucesivas C n+2, C n+4, C n+6... Por supuesto, esto no influye en los coeficientes C n+1, C n+3,... De tal modo, con el fin de garantizar una función de onda acotada, debemos separar primero los términos pares e impares en dos series de potencias independientes:
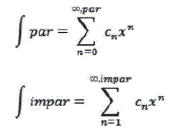
Necesitamos que las funciones de onda mismas se encuentren formadas por e-ax2/2 multiplicada exclusivamente por una suma de términos impares o por una suma de términos pares. Ahora se requiere que en el caso de cada suma, con el fin de que la función de onda no sea infinita, en algún valor de n el siguiente coeficiente C n+2 debe ser cero. De esta manera, también serán cero todos los demás coeficientes. Como la fórmula de recursión permite calcular el coeficiente C n+2 a partir de la constante anterior Cn , podemos sustituir C . por cero:
![]()
La única manera de que el coeficiente C n+2 se anule consiste en que el numerador de la fracción en la ecuación anterior se vuelva cero en dicho valor de n:
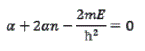
Esta expresión incluye la energía total E del oscilador armónico. Como la energía constituye un importante observable, haremos un alto para analizarla. Con el propósito de que la función de onda no sea infinita, la energía del oscilador armónico, al combinarse con otros términos como a, n, m y h, debe tener sólo aquellos valores que satisfacen la ecuación anterior. Por lo tanto, podemos resolverla para aquellos valores de energía adecuados. Asimismo, si sustituimos ![]() , obtenemos una conclusión simple:
, obtenemos una conclusión simple:

donde n es el valor del índice con respecto al cual el siguiente coeficiente de la serie se vuelve cero, h es la constante de Planck y v es la frecuencia clásica del oscilador. Es decir, que la energía total del oscilador armónico depende exclusivamente de su frecuencia clásica (determinada por su masa y la constante de fuerza), la constante de Planck y el entero n. Como la energía sólo puede poseer los valores que determina su ecuación, la energía total del oscilador armónico se encuentra cuantizada. El índice n es el número cuántico, y puede tener valores de 0 a infinito. (González Gaxiola O.,2004 : 55).
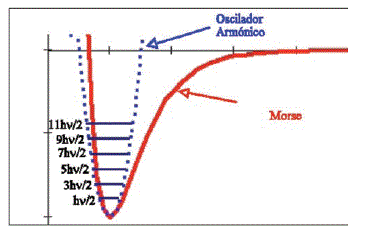
Antes de volver a las funciones de onda, hay unos cuantos puntos a considerar con respecto a la energía total. La figura muestra un diagrama de los niveles de energía para diferentes números cuánticos (suponiendo que la masa y la constante de fuerza no cambian). En el caso de un oscilador armónico ideal, los niveles de energía se encuentran espaciados la misma cantidad. Es fácil demostrar que los niveles de energía se encuentran separados por AE=hv. Además, el valor mínimo posible para la energía no es cero. Esto se observa sustituyendo el mínimo valor posible del número cuántico n, que es cero. Así,
![]()
que es un valor diferente de cero para la energía total. Esto introduce el concepto de energía de punto cero. En el valor mínimo del número cuántico (el estado fundamental del oscilador), todavía existe en el sistema una cantidad de energía diferente de cero ( Bròdy T. A.,1959 :144).
CONCLUSIONES
Se resolvió la ecuación de Schrodinger independiente del tiempo para el oscilador armónico cuántico . obteniéndose la energía del oscilador .Es importante hacer notar que los osciladores cuánticos no pueden tener energía cero , con las moléculas ocurre lo mismo estas no pueden tener energía de vibración cero, siendo su energía mínima hv/2 .Esta energía origina la vibración del enlace incluso a 0 K . Un oscilador cuántico y por lo tanto la molécula no puede tener cualquier cantidad de energía de vibración .Este tipo de oscilador solo admite cantidades de energía proporcionales a hv/2 , es decir la energía esta cuantizada .La mayoría de las moléculas no poseen energía suficiente para situarse en estados excitados de vibración , si pueden excitarse mediante absorción de radiación de energía E1 -Eo = hv, este fenómeno es el origen de los espectros de vibración o espectros infrarrojos IR; es decir los espectros de IR surgen a consecuencia de la variación discontinua de la energía de vibración de una molécula debido a la absorción de radiación.
BIBLIOGRAFÍA
Arrieta A., Arrieta E.S. & Tejeiros J. M. (2009). "Masa Efectiva para un Sistema de Muelle Real" en Revista Colombiana de Física, vol. 41, No. 2, (517-519). [ Links ]
Atkins, P. & de Paula, J. (2008) Química Fisica 8o edicion .Buenos Aires:Panamericana. pag.278-293 [ Links ]
BallW. D. (2004) Fisicoquímica.Thomson ed. México DF.pag.273-307 [ Links ]
Porta A & Sandoval J.L. (1987). " Oscilaciones armónicas: Un experimento completo [ Links ]
Bròdy T. A. (1959). "Brackets de transformación para funciones de oscilador armónico" en Revista Mexicana de Fisica Vol. VIII, 3, (139-228) [ Links ]
García Barneto A. & Bolívar Raya J. P. (2008). "Efecto de las simulaciones interactivas sobre las concepciones de los alumnos en relación con el movimiento armónico simple" en Revista Electrónica de Enseñanza de las Ciencias Vol. 7 N°3, (681-703). [ Links ]
González Gaxiola O. & Quezada Batalla R. "El proceso de Ornstein-Uhlenbeck, el oscilador armónico cuántico y la fórmula de Feynman-Kac". Departamento de Matemáticas UAM-Iztapalapa, (1-15). [ Links ]
González Gaxiola O. & Quezada Batalla R. (2004). "El proceso de Ornstein-Uhlenbeck, el oscilador armónico cuántico y la fórmula de Feynman-Kac" en Miscelánea Matemática 40 (53-67). [ Links ]
Morales Leal F." en Revista Mexicana de Física 33 No. 9, (499-512). [ Links ]
Pogosyan G. S., Vicent L. E. & Wolf K. B. (2005). "El límite del oscilador cuántico a la partícula libre" en Revista Mexicana de Física E 51 (1), (18-22). [ Links ]
Quintero Zuluaga J.J. (2002). "Espectro semiclàsico usando el propagador de Herman-Kluk" en Revista Colombiana de Física VOL. 34, No. 1, (59-62). [ Links ]













