ARTICULOS DE INVESTIGACIONES FACULTATIVOS DOCENTE

 

Introducción a la termodinámica con derivadas parciales

 

 

CASTAÑETA, HERIBERTO¹ NOGALES, JORGE¹ ZOTA, VIRGINIA¹
CORRESPONDENCIA: VIRGINIA ZOTA AVIRZOTAU@YAHOO.COM
¹ Facultad de Ciencias Farmacéuticas y Bioquímicas. Av. Saavedra No. 2224 La Paz - Bolivia

FECHA DE RECEPCIÓN: 16 DE ABRIL DE 201
FECHA DE ACEPTACIÓN 30 DE JULIO DE 2014

 

 

---

Resumen

Este artículo es una revisión de los principios de la termodinámica utilizando el cálculo diferencial parcial. Inicialmente, una breve visión general de los conceptos y definiciones de las derivadas parciales y algunas reglas están hechas. Diferencial exacta e inexacta y el próximo, se definieron las funciones del Estado y el primero y segundo principios o leyes de la termodinámica. Las cuatro relaciones de Maxwell se deducen y algunas aplicaciones se presentan. La facilidad para deducir expresiones matemáticas con derivadas parciales es uno de los recursos más importantes de las matemáticas de la termodinámica. Estos son parte de una herramienta útil; bien es cierto que pueden llegar a ser complejo, sin embargo, conocer y decir mucho más acerca de un sistema con la ayuda de estas herramientas.

PALABRAS CLAVE

Termodinámica, derivados parciales, relaciones de Maxwell

---

Abstract

This article is a review of the principles of thermodynamics using partial differen-tial calculus. Initially, a brief overview of the concepts and definitions of partial de-rivatives and some rules are made. Exact and inexact differential and next, it's de-fined the functions of state and the 1stand 2nd principles or laws of thermodynamics. The four Maxwell relations are deduced and some applications are presented. The facility to deduced mathematics expres-sions with partial derivatives is one of the most important resources of mathematics of thermodynamics. This are part of a useful tool; it's true that they can become com-plex, however we know and tell much more about a system with the help of this tools.

KEY WORDS

Thermodynamics, Partial derivatives, Maxwell relations

---

 

 

INTRODUCCIÓN

La termodinámica es una ciencia (Furió, 2007: 463) de la química y de la fisicoquímica pura y aplicada muy utilizada en el conocimiento de los parámetros energéticos y de estabilidad de moléculas y biomoléculas en bioquímica y en el diseño y formulación de preparados farmacéuticos en tecnología farmacéutica.

La termodinámica hace amplio uso del cálculo diferencial e integral, especialmente de las derivadas parciales. Las expresiones deducidas en termodinámica aplicando la derivación parcial son muy útiles, ya que el comportamiento de un sistema que no sea susceptible de medición directa puede describirse mediante las expresiones obtenidas por derivación parcial o el uso de herramientas virtuales. (Quiñones, 2006:1423)

Para referirnos a las derivadas de una función, en principio consideremos y simbolicemos algunas funciones que se presentan en la vida real.

Por ejemplo: el estado del agua depende de la temperatura; para habilitar un equipo electrónico, éste depende de su batería; el celular depende al menos de las siguientes componentes la batería, el chip, la señal; el hombre depende de las siguientes variables más relevantes la presión cardíaca, presión arterial, temperatura, peso, talla; en la ecuación de estado el volumen V depende de P, n, R, T.

La derivada de una función es la razón de cambio de una variable, de forma gráfica es la tangente a la curva en un punto. Así la velocidad de un móvil es la distancia recorrida respecto al tiempo; en el caso del hombre si la meta es que cambie el peso, ésta es la única variable que cambia, no así las otras consideradas (si por bajar de peso hace dieta hecho que incide en su peso, no así en su talla), en consecuencia ésta es una derivada parcial.

En las ecuaciones de estado por ejemplo PV=nRT las derivadas parciales ayudan a determinar el efecto que el cambio en una de las variables de estado provoca en otra de ellas, para conseguir esto necesitamos de las herramientas del cálculo.

Una pendiente es una derivada y una derivada es una pendiente, para representar en forma gráfica la dependencia de y respecto a x, si denotamos y por f(x), entonces

 

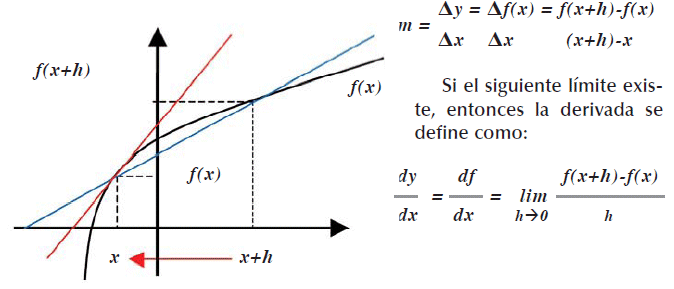
Ahora consideramos una función de varias variables, denotada por f la derivada parcial def respecto a una variable denotada por se define como:

 

siempre que el limite exista. Se denomina así porque sólo una de sus variables es la que cambia, las restantes variables se mantienen constantes. Las derivadas de orden superior, cumplen la definición.

En las ecuaciones con varias variables como PV= nRT la derivada total de una función F de variables múltiples x, y, z simbolizada como F(x, y, z) es la suma de todas sus derivadas parciales cada una de ellas multiplicada por el cambio infinitesimal en la variable apropiada (dx, dy, dz y así sucesivamente):

 

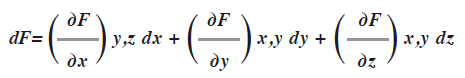
Se lee: la derivada de la función F con respecto a una variable a la vez. En cada caso las demás variables se mantienen constantes.

Con las ecuaciones de estado podemos derivar y determinar expresiones para los cambios de una variable de estado con respecto a la otra. Algunas veces estas derivadas nos permiten obtener conclusiones importantes sobre las relaciones entre las variables de estado, lo que constituye una técnica poderosa para trabajar con la termodinámica. (Atkins, 2008:57)

 

DERIVADAS PARCIALES Y LEYES DE LOS GASES

En la ecuación de estado PV=nRT supongamos que necesitamos conocer la forma en que varia la presión con respecto a la temperatura T suponiendo que el volumen Vy el número de moles n en nuestro sistema gaseoso permanece constante. Esta interrogante que nos interesa la podemos escribir con una derivada parcial:(Levine, I. 2004:23).

Es posible construir diversas derivadas parciales que relacionen las diferentes variables de estado de un gas ideal, algunas de las cuales son más útiles o fáciles de entender que otras, no obstante la derivada de R es cero ya queR es una constante (Bonilla, 2006:65).

En la ecuación de estado PV=nRT, analicemos V,n,R a partir de P=nRT/V luego derivar ambos miembros con respecto a T, mientras el resto de las variables se mantienen constantes:

 

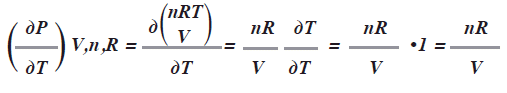
Si tomamos una muestra de un gas ideal y medimos su presión P a diferentes temperaturas T a volumen constante y trazamos la grafica, obtenemos una recta cuya pendiente es (nR/ V) es decir la derivada. (Acevedo, R. & Costas, 2007:174). Luego el cambio de presiónrespecto a la temperatura T es {dpi dT)V,n,R = V/nR.

Si A es función de dos variables B y C representada A(B,C) y ambas variables B y C son funciones de las variables D y E representado B(D,E) y C(D,E), entonces la regla de la cadena para las derivadas parciales es:

 

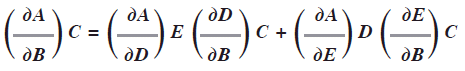
En los casos de PVT podemos aplicar este concepto; dada una cantidad de gas, la P depende de Vy T:P(V,T) y el volumen depende dePy T: V(P,T) y la temperatura depende de P y V: T(P,V). En el caso de cualquier variable de estado general de un gas F la derivada total de esta con respecto a la temperatura T a P constante, es:

 

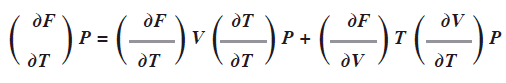
El termino la derivada de una variable respecto a si misma es 1, en otro caso 0.

Si F es la presión P entonces puesto que P se mantiene constante. La expresión anterior se convierte en:

 

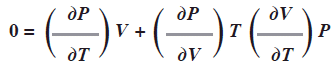
Podemos reordenar esta expresión

 

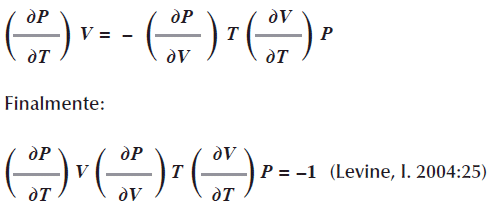
Observe que cada término incluye PVT; si se conoce cualquiera de las dos derivadas, se puede determinar la tercera.

El coeficiente de expansión de un gas ideal a se define como el cambio en el volumen conforme la temperatura cambia a presión constante, la expresión incluye el factor 1/v:

 

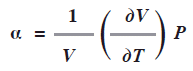
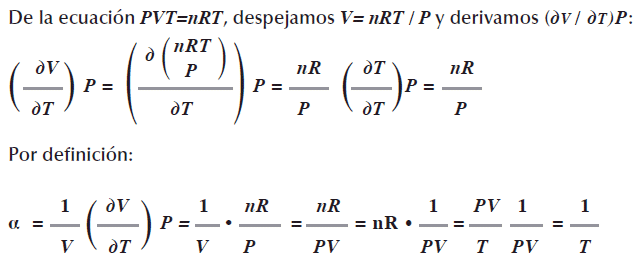
La compresibilidad isotérmica de un gas representado con la letra K es el cambio del volumen conforme varía la presión a temperatura constante con factor 1/V:

 

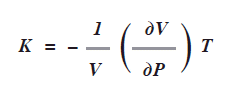
Siguiendo el procedimiento anterior, para un gas ideal se demuestra que K=nRT/VP²

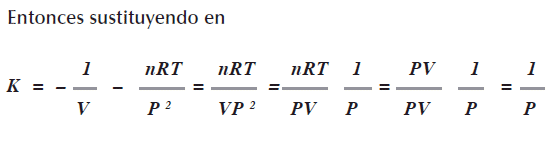
Ya que las dos definiciones utilizan PVT se tiene (dp / dr)V = a / T, en efecto:

 

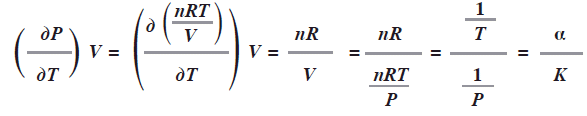
Estas expresiones son de interés cuando es imposible mantener el volumen de un sistema constante. La derivada del volumen constante puede expresarse en términos de derivadas a temperatura y presión constantes, dos condiciones fáciles de controlar en laboratorio. (Bonilla, 2006:67-68)

Consideremos un proceso físico o químico que ocurre en un sistema, este tiene unas condiciones iniciales y después del proceso tendrá otras condiciones, finales; pero hay muchas formas en que el sistema pueda pasar de su estado inicial a su estado final. Una función de estado es cualquier propiedad termodinámica del sistema cuyo cambio durante el proceso es independiente de la trayectoria, esto es, que depende solo del estado del sistema (PVTn) y no de la historia del sistema o de como este llegó a dicho estado. Las funciones de estado se representan con letras mayúsculas. Como la energía interna U, entalpia H, entropía S, energía libre de Helmholtz A, energía libre deGibbs G.

Una propiedad termodinámica cuyo cambio durante el proceso depende de la trayectoria no es una función de estado. Las funciones que no son de estado se representan con letras minúsculas, tales como el trabajo w y el calor q. (Atkins, 2008:57)

Existe otra diferencia en lo que se refiere a las funciones de estado. Cuando se presenta una variación infinitesimal en un sistema, las variaciones infinitesimales en el trabajo w y el calor q y la energía interna se representan así: dw, dq, dU respectivamente. En un proceso completo estos cambios infinitesimales se integran desde las condiciones iniciales hasta las finales. Hay una diferencia en la notación: cuando se integran dw, dq el resultado es la cantidad absoluta de trabajo wyde calor q asociados al proceso. Pero cuando se integra dU en resultado no es U absoluto sino el cambio en .

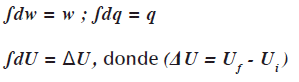
La misma relación existe para las otras funciones de estado. Las diferenciales son diferenciales inexactas, significa que sus valores integrados w y q dependen de la trayectoria.

En cambio dU es una diferencial exacta, quiere decir que su valor integrado AU es independiente de la trayectoria. Todos los cambios en las funciones de estado son diferenciales exactas. (Atkins, 2008:58)

 

PRIMERA LEY DE LA TERMODINÁMICA

La energía interna U es la energía total de un sistema, representa el total de la energía cuando se suma la energía cinética y la energía potencial del sistema.

La energía cinética debida al movimiento molecular y atómico y la energía potencial debida a la posición entre moléculas y entre átomos.

La energía interna, más concretamente la variación de la energía interna dU de un sistema puede variar cuando se agrega calor al sistema o cuando el sistema emite calor dq y cuando el trabajo es realizado por el sistema o si se realiza trabajo sobre el sistema.

Si tenemos un sistema gaseoso que contiene un volumen de partículas determinado, estas se encuentran en movimiento se desplazan, entonces tienen velocidad por tanto tienen energía cinética E.C; las partículas se encuentran en una determinada posición entonces pueden interactuar entre ellas esto representa una energía potencial E.P; toda esta energía se necesita para poder existir como sistema, es la energía para mover a las partículas y estar entrelazados a través de las fuerzas internas que poseen (E.C y E.P ) y la suma de estas nos da la energía interna U, que no incluye la energía para formarlo.

Lo que plantea la primera ley de la termodinámica es que si se toma un sistema con un volumen determinado y que tiene energía interna U y procedemos a calentar al sistema por ej., agregándole calor, vamos a poder incrementar la energía interna, pero adicionalmente si comprimimos al sistema aplicando una fuerza F sobre una superficie del sistema, éste varía su volumen, por tanto estamos realizando trabajo estamos agregando trabajo, una forma de energía y también logramos incrementar la energía interna del sistema. (Atkins, 2008:58-63)

La energía interna U puede variar cuando le agregamos calor o efectuamos trabajo w sobre el sistema. En forma de ecuación:

De manera literal: la variación de la energía interna dU (dieferencial exacta) es igual al calor dq (diferencial inexacto) agregado al sistema más el trabajo dw (diferencial inexacto) que realizamos sobre el sistema.

Esta es la primera ley o primer principio de la termodinámica.

Si queremos reducir la energía interna U se puede forzar a que el sistema haga trabajo o ceda calor: dU = dq - dw que es también una forma de la primera ley de la termodinámica.

Explicaremos un poco en que consiste el trabajo w. Si tenemos un volumen de gas y comprimimos con una fuerza F sobre una superficie S y logramos que el sistema se angoste en dx, hemos hecho camino dx con una fuerza dw = Fdx; por definición la presión P = F/S y F = PS.

Entonces dw = F .dx también dw = PS . dx y el productoS .dx (superficie por variación de distancia) es variación de volumen dv por tanto dw = P.S.dx lo expresamos como dw = P dv; al aplicar la fuerza F estamos reduciendo el volumen y la variación de volumen será negativa dv(-) o dv < 0 pero hacemos trabajo w positivo porque aumentamos la energía del sistema, en consecuencia aplicamos un signo negativo a la expresión: dw = -Pdv que es el trabajo realizado sobre el sistema. Al aplicar la expresión de trabajo obtenida en la definición de la primera ley de la termodinámica:

, que es también una forma de la primera ley de la termodinámica o ley de la conservación de la energía.

 

SEGUNDA LEY DE LA TERMODINÁMICA

Supongamos que tenemos dos sistemas separados por una pared rígida, entonces no habrá variación de volumen dv₁ + dv₂= 0.

Por tanto no se podrá realizar trabajo dv₁ + dv₂ = 0. Los dos sistemas se encuentran a una temperatura T₁ y T₂ y además supondremos que la temperatura del sistema 1 es mayor a la del sistema 2T₁>T₂.

Para realizar cualquier cambio, por ej., desplazar calor dq del sistema 1 al sistema 2 o viceversa por la diferencia de temperatura; esto afectará a la energía interna U de ambos sistemas y considerando la ley de la conservación de la energía: dU₁ + dU₂ = 0

Si T₁ > T₂ significa que el sistema 1 tiene mayor energía que el sistema 2; la energía fluirá en forma de calor del sistema 1 al sistema 2 (la energía del sistema 2 aumentará mientras que la energía del sistema 2 disminuirá) hasta que ambos sistemas tengan la misma energía, esto sucede de manera espontánea. (Villanueva, 2009:145)

Cuando pasa energía de un sistema de mayor energía a un sistema de menor energía, este flujo de energía sucede hasta que ambos sistemas tengan la misma energía, esta distribución o redistribución de energía es la entropía simbolizado con la letra S.

Sin embargo, la ecuación dU = dq + dw no prohíbe el flujo de energía del sistema 2 al sistema 1, es decir el paso de energía de un sistema de menor contenido energético a otro de mayor contenido energético, siempre y cuando la 1ra ley se exprese, es decir mientras que la energía total se conserve dU₁ +dU₂=0 la primera ley de la termodinámica tiene un problema, no acota al sistema, no existe un cambio espontaneo como el que un sistema de baja energía entregue energía a un sistema de mayor energía (a excepción de un refrigerador); se puede lograr este pasaje de energía pero realizando trabajo.

La entropía S, más concretamente dS varía en función del calor dq, es decir dS =dq / T

La segunda ley de la termodinámica establece que la dS > 0. (Villanueva -Marroquín, J. & Barragán D., 2009:148).

 

POTENCIALES TERMODINÁMICOS

En ésta sección, deduciremos matemáticamente a las cuatro relaciones de Maxwell a través de los potenciales termodinámicos como energía interna U, entalpia H, energía libre Gibbs G y energía libre de Helmholtz A. (Herrera, J. N, 2011: 78).

La primera ley de la termodinámica establece:

La segunda ley de la termodinámica afirma:

Reemplazando dq en la 1ra ley tenemos las siguientes expresiones:

De ésta ecuación diferencial concluimos que la energía interna U es función de la entropía S y del volumen U = U(S,v), expresando esto con derivadas parciales (Acevedo, R. & Costas, 2007:175), tenemos:

 

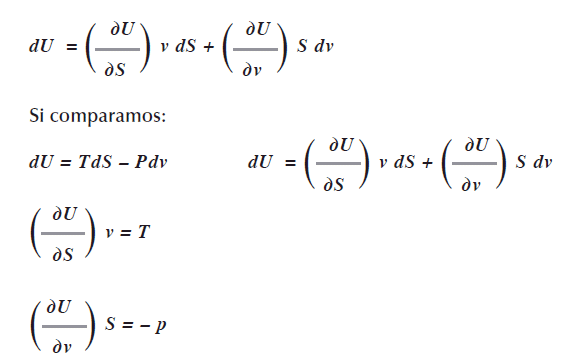
Como usamos un diferencial exacto significa que las derivadas cruzadas entre estos factores tienen que ser iguales, esto es:

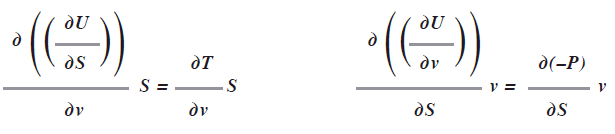
La energía interna U es la energía del sistema, ésta energía no incluye la energía para formar al sistema; por ej., en una transición de estado, en la fusión, el sólido pasa al estado liquido como el hielo a agua líquida, para que el agua exista hay que generar un espacio, esto significa agregar trabajo (Pv) para que exista ese sistema, esto es: U + Pv, ésta energía es la entalpia H, en forma simbólica es H = U + Pv.

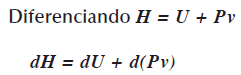
Entonces la entalpia H es función de la entropía S y de la presión P, esto esH = H(S,P).

 

Al derivar en forma cruzada las dos últimas ecuaciones, se tiene:

Con ésta relación no necesitaremos medir el cambio de volumen con respecto a la entropía a presión constante porque este es equivalente al cambio isoentrópico de la temperatura con respecto a la presión.

La limitación de la primera ley de la termodinámica dU = dq + dw, es el calor (Pérez, 2007:1) dq (dq = TdS de la definición de entropía). Si un sistema realiza trabajo, la conversión de la U en trabajo es ineficiente, la U hace trabajo pero además genera calor (TS); entonces la energía que queda libre para realizar trabajo es la energía libre de Helmholtz A. A = U-TS (TS, es el calor). Diferenciando ésta relación:

La energía libre de Helmholtz depende del volumen y la temperatura: A=A(v, T) esta afirmación expresada en derivadas parciales:

La energía libre de Gibbs considera a la entalpia H no a la energía interna U, menos el calor (TS):G = H-TS

 

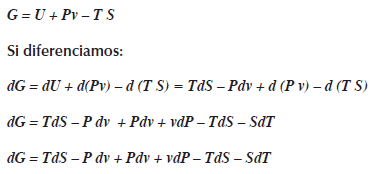
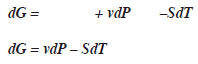
La energía libre de Gibbs varía en función a la presión y temperatura G=G(P,T).

 

Al derivar en forma parcial las dos últimas ecuaciones respecto a y respectivamente, se tiene la cuarta relación de Maxwell.

 

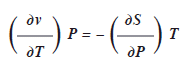
Las relaciones deducidas, reciben esa denominación en honor al matemático y físico Escoses James Clerck Maxwell.

Las relaciones de Maxwell son útiles por dos razones:

Primero, todas las relaciones se pueden aplicar; no están restringidas a los gases ideales, se aplican a sistemas líquidos y sólidos.

Segundo, expresan determinadas relaciones en términos de variables fáciles de medir.

Por ej., podría resultar difícil de medir directamente la entropía y determinar cómo varía con respecto al volumen a temperatura constante La tercera relación de Maxwell muestra que no tenemos que medirla directamente, si medimos el cambio de la presión con respecto a la temperatura a volumen constante obtenemos . Estas son iguales. (Rojas, W. A., 2008: 233)

Las relaciones de Maxwell también resultan útiles en la deducción de nuevas ecuaciones que puedan aplicarse a los cambios termodinámicos en sistemas, o en la determinación de valores de cambios en funciones de estado que podrían resultar difíciles de medir directamente experimentalmente.

 

APLICACION DE LAS RELACIONES DE MAXWELL

Las relaciones de Maxwell pueden ser sumamente útiles en la deducción de otras ecuaciones para la termodinámica. Por ej.: como dH = TdS + vdP

Si mantenemosconstante y dividimos toda la expresión entre dP, tendremos:

 

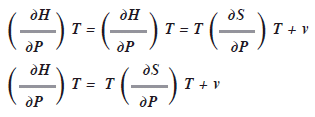
Es difícil medir el cambio de entropía con respecto a la presión, pero si utilizamos una relación de Maxwell, podemos sustituirla por otra expresión. Como la cuarta relación de Maxwell entonces:

 

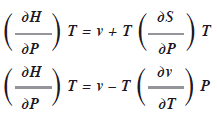
Aquí se cambio el orden de los términos. Por ej. si conocemos, la ecuación de estado de los gases ideales y conocemos y la variación de v con respecto aa presión constante, esta información podemos utilizar para calcular la variación de la entalpia con respecto a la presión a temperatura constantesin tener que medir la entalpia.

Supongamos que deseamos conocer la para un gas que se comporta de acuerdo con la ecuación de estado de Van Der Waals.

 

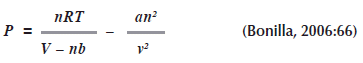
Si derivamos con respecto a a volumen constante sobre la ecuación de Van Der Waals (recuerde que son constantes ), tenemos:

 

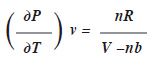
Por la tercera relación de Maxwell

 

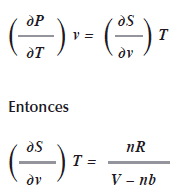
También se ha deducido en la ley de los gases que

 

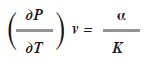
Donde a es el coeficiente de expansión y es la compresibilidad isotérmica. Para el mercurio ; determinaremos el cambio de entropía con respecto al volumen bajo condiciones isotérmicas, es decir

La tercera relación de Maxwell afirma que

 

CONCLUSIONES

La facilidad para deducir expresiones matemáticas con derivadas parciales es uno de los principales recursos de las matemáticas de la termodinámica. Estas constituyen una herramienta útil; es cierto que puedan tornarse complejas; sin embargo, podemos saber y decir mucho sobre un sistema con la ayuda de estas herramientas, y en última instancia, esto constituye la esencia de la fisicoquímica.

 

REFERENCIAS

Quiñones, C., Ramírez, D., Rodríguez, Z., Rivera, F., Tovar, E., Vasquez, G. & Ramirez, A. (2006) Desarrollo de herramientas virtuales para la enseñanza de la Termodinámica básica. Revista Colombiana de Física, 38(4), 1723-1426.        [ Links ]

Furió-Gómez, C., Solbes, J. & Furió-Mas, C. (2007) La historia del primer principio de la termodinámica y sus implicaciones didácticas. Revista Eureka sobre Enseñanza y Divulgación de las Ciencias, 4(3), 461-475.        [ Links ]

Bonilla B. & Herrera J. N. (2006) Revisando la ecuación de Van der Waals. Revista Mexicana de Física, 52(1), 65-77.        [ Links ]

Acevedo-Chávez, R. & Costas, M. E. (2007) Response coefficients in thermodyna-mic systems (I). Revista Mexicana de Física, 53(2), 174-177.        [ Links ]

Herrera, J. N., Salazar- Govea, A. Y., Cruz Vera, A. & González- Jiménez, E. (2011) Thermodynamic properties of simple milti-Yukawa fluids: a variational ap-proach. Revista Mexicana de Física, 57(1), 78-82.        [ Links ]

Villanueva - Marroquín, J. & Barragán D. (2009) Análisis de la producción de Entropía en una máquina térmica operada con un sistema químico no-lineal. Revista Mexicana de Ingeniería Química, 8(1), 145-152.        [ Links ]

Rojas, W. A. & Arenas J. R. (2008) Transformaciones de cantidades termodinámicas en el Régimen de la Teoría Espacial de la Relatividad. Revista Colombiana de Física, 40(1), 233-236.        [ Links ]

Pérez-Cruz, J.R. (2007) La termodinámica de Carnot a Clausius. Conferencia impartida en el curso "La ciencia Europea antes de la Gran Guerra" Organizado por la fundación Canaria Orotava de Historia de la Ciencia. En La Orotava (Tenerife) y las Palmas de Gran Canaria, 1-21.        [ Links ]

Atkins, P. & de Paula, J. (2008) Química Física. Buenos Aires: Panamericana. Pág.57-65        [ Links ]

Levine, I. (2004) Físico Química. España: Mc Graw Hill, Interamericana, pág.20-30        [ Links ]

Zota, U.Virginia. (2001) Geometría Analítica y Cálculo, La Paz        [ Links ]

Finney, Thomas (1987) Cálculo Con Geometría Analítica, Addison-wesley Iberoamericana.        [ Links ]

Castellan Gilbert, W. (1980) Fisicoquímica, University of Maryland.        [ Links ]