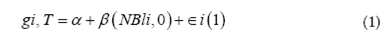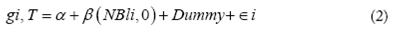Izquierda: Vista de la esquina de las calles Ayacucho y Colón obtenida desde el frente de la iglesia “La Merced’’- Año 1960 aproximadamente. Derecha: Vista de la esquina de las calles Ayacucho y Colón obtenida desde el frente de la iglesia “La Merced’’- Vista de la casa comercial de ropa infantil y juvenil “Chimichurri’’- Año 2005.
1. Introducción
A mediados de los ochenta, el fin del proceso hiperinflacionario boliviano trajo consigo cambios radicales en la estructura, organización y funcionamiento del Estado. La crítica situación surgida a raíz de las políticas del gobierno izquierdista de la Unidad Democrática y Popular (UDP) obligaba a tomar medidas extremas para acabar con el incontrolable aumento de precios y modernizar el Estado (Morales y Sachs, 1987). Aunque es cierto que las medidas adoptadas en 1985 fueron dolorosas, no lo es menos que se logró contener la hiperinflación e ingresar, según Morales (2009), a una senda de crecimiento moderado del producto interno bruto (PIB), aunque altamente dependiente de la situación económica mundial.
El efecto de los cambios estructurales que tuvieron lugar a mediados de la década del ochenta, así como la evolución de los agregados macroeconómicos post-hiperinflación fueron objeto de numerosos estudios académicos, los cuales se multiplicaron a partir de las nuevas teorías económicas y los avances en la informática lo que permitió realizar cálculos con mayor precisión y velocidad. Sin embargo, hasta el presente, la mayoría de las investigaciones macroeconómicas -sobre convergencia u otros temas- se han limitado a investigar los datos agregados a nivel país o a nivel departamento, esto debido principalmente a la falta de datos confiables y continuos en el tiempo. En general, se podría decir que los trabajos a escala municipal son más bien la excepción, lo cual se vuelve evidente por el gran vacío existente respecto a las investigaciones de tipo académico a nivel de municipios.
En este sentido, una de las áreas de investigación que se ha venido desarro llando para Bolivia a nivel departamental es la de convergencia beta (Barro, 1991; Barro y Salai-Martin, 1992), entendida como el fenómeno en el cual las regiones con menores ingresos per cápita crecen a tasas más altas que aquellas regiones con mayores ingresos, y, por lo tanto, ambas tienden eventualmente a converger hacia un mismo estado estacionario. En otras palabras, las regiones más pobres tienden a acortar la distancia que las separa de las regiones más ricas.
Viendo lo anteriormente expuesto, el presente trabajo se ha fijado tres obje tivos. Primero, analizar la existencia de convergencia beta usando como "proxy" de pobreza el Índice de Necesidades Básicas Insatisfechas (NBI) para los municipios del departamento de Santa Cruz. Siguiendo la intuición de los modelos de convergencia -vale decir, que las regiones rezagadas crezcan a ma yores tasas para acortar la distancia con las regiones más prósperas- se espera que aquellos municipios con más necesidades básicas insatisfechas canalicen sus recursos y esfuerzos a cubrir las mismas, ya que, por definición, al ser nece sidades básicas existirá mayor urgencia de cubrirlas, y, por lo tanto, una mayor proporción de sus recursos se destinarán a atender estas necesidades.
Por otro lado, los municipios que ya tuviesen cubiertas la mayor parte de sus necesidades básicas destinarán una menor proporción de recursos a las mismas. Eventualmente, los municipios que canalicen más recursos (o sea, los que inicialmente tienen más necesidades básicas insatisfechas) tenderán a igualarse (converger) en la cobertura de necesidades básicas con aquellos municipios que destinan -proporcionalmente- menos recursos (en otros términos, los municipios más ricos).
Segundo, el periodo elegido para nuestro estudio coincide con uno de los cambios estructurales más importantes que tuvo lugar a finales del siglo pasado, específicamente la ley 1551 de Participación Popular (PP) la cual entra en vigencia en el año 1994 hasta su abrogación en el año 2010. Nuestros datos comienzan dos años antes y terminan dos años después, vale decir que abarcan desde el año 1992 hasta el año 2012 por lo que se cubre todo el periodo de vigencia de la ley. Este no es un detalle menor, ya que justamente uno de los objetivos de esta ley fue la de "municipalizar" el país mediante la transferencia de recursos y, por lo tanto, era de esperarse que la ley de PP hubiese sido un catalizador del proceso de convergencia. Nuestra investigación se ha fijado como objetivo analizar si en efecto ha existido este proceso de convergencia en los municipios del departamento de Santa Cruz durante el periodo de la ley de PP.
Finalmente, como se dijo con anterioridad, las investigaciones económicas a nivel municipal en Bolivia son muy escasas, por lo que esperamos que esta investigación sea un aporte para llenar ese vacío en la literatura. En cualquier caso, nuestro análisis debe tomarse como una primera aproximación.
El artículo procede de la siguiente forma: en el siguiente capítulo realizamos una revisión sobre la literatura, así como la descripción teórica del modelo de convergencia; en el capítulo III presentamos los datos y el modelo econométrico; en el capítulo IV evaluamos los resultados y concluimos en el capítulo V.
2. Revisión de la literatura
El análisis del crecimiento económico ha sido parte del núcleo de estudio de la economía desde sus inicios, pero no fue sino hasta mediados del siglo pasado cuando los trabajos de Solow (1956) y Swan (1956) formalizaron teóricamente los periodos de ajustes de las economías para llegar a lo que se conoce como el estado estacionario1. Una de las implicaciones del modelo de Solow es que, dadas dos economías con idénticas estructuras, pero distintos niveles de producto per cápita y de acumulación de capital, la tasa de crecimiento del producto será mayor en aquella economía más pobre ( dicho de otro modo, la que tiene un menor nivel de producto per cápita y acumulación de capital). Esto implicará que la velocidad con la que ambas crecerán será distinta, y por tanto, la economía que se encuentra rezagada -al crecer a tasas más altas-eventualmente alcanzará la economía más próspera y ocurrirá lo que se conoce como convergencia absoluta2.
Los trabajos seminales de Baumol (1986) y Barro (1991) iniciaron una nueva era en el análisis empírico de convergencia. En ambos casos se presentó suficiente evidencia sobre la existencia de convergencia a nivel internacional, aunque se haya empleado distintos periodos de análisis, así como distintos conjuntos de países. De especial interés para nosotros resulta el trabajo de Barro y Sala-i-Martin (1992), ya que, a diferencia de los anteriores, este no analiza la existencia de convergencia entre países, sino entre regiones dentro de un país. Sus resultados encuentran evidencia de convergencia para los estados pertenecientes a Estados Unidos en el periodo desde 1880 hasta 1988, así como para subperiodos de 10 años divididos de forma tal que el comienzo del periodo concuerde con el comienzo de un nuevo decenio. Este enfoque regional comporta ventajas para la búsqueda de convergencia absoluta, ya que hace más plausible el supuesto de estructuras económicas idénticas.
Posterior al trabajo de Barro y Salai-Martin (1992), surgió una plétora de investigaciones, todas ellas con la intención de encontrar evidencia empírica sobre la existencia -o no- de convergencia beta. Las investigaciones no se limitaron al análisis de convergencia absoluta o de datos de corte transversal, ya que la literatura se fue enriqueciendo con nuevas técnicas. Por ejemplo, Islam (1995) propone el uso de datos de panel y un conjunto de estimadores para estudiar el tema de convergencia. Incluso se ha propuesto el uso de variables espacialmente ponderadas y técnicas espaciales tendientes a captar el efecto que las regiones vecinas pudiesen tener sobre la velocidad de convergencia (Arbia,2006).
Entre los trabajos que encontraron evidencia de convergencia beta a nivel regional -es decir, dentro de las regiones de un país- están, sólo por citar algunos, Sala-i-Martin (1996) para Japón, Alemania, Reino Unido, Francia, España y Canadá; Lehmann, Oshchepkov y Silvagni (2020) para Rusia; Bajpai y Sachs (1996 para India; Rodríguez-Gamez y Cabrera-Pereyra (2020) para México; Serra et al. (2006) para Brasil, Colombia, Chile y Perú. Pero también existen trabajos que no encontraron convergencia beta: Garrido, Marina y Sotelsek (2001) para Argentina; Siriopoulos y Asteriou (1998) para Grecia y Serra et al. (2006) para México.
En cuanto a los estudios de convergencia beta para Bolivia, los trabajos de Montero Kuscevic y Río Rivera (2013), Méndez-Guerra (2017) más el de Caballero y Caballero Martínez (2016) presentan evidencia sobre la existencia de convergencia beta en los departamentos de Bolivia para el periodo 1988-2014; sin embargo, no encontraron convergencia para el periodo 1988-20003. A nivel municipal, Méndez-Guerra (2018) analiza la convergencia en el desarrollo humano para los 20 municipios más grandes. El autor encuentra evidencia de convergencia en el desarrollo humano para el periodo 1992-2013.
Aunque la literatura sobre convergencia es muy rica y variada, hay un tema específico que nos interesa, y se refiere a los llamados clubes de convergencia. En otros términos, la existencia de distintos estados estacionarios dependiendo de la estructura particular de cada región, así como de su ingreso per cápita inicial (Darlauf y Johnson, 1995). La importancia de los clubes de convergencia, así como su continua vigencia en la agenda de investigación, se hace evidente por la abundante literatura (Tian et al., 2016; Barrios, Flores y Martínez, 2019; Mendoza-Velázquez et al., 2020)
3. Modelación econométrica y datos
3.1. Modelación econométrica
Algunos de los temas de discusión recurrente en el momento de analizar empíricamente las teorías económicas son el enfoque y la metodología que se van a emplear y, en ese sentido, el análisis de la convergencia beta no consti tuye la excepción. Es así que la modelación se puede hacer con datos de corte transversal o datos de panel. Se pueden usar estimaciones lineales o no lineales. Además, hay que decidir entre convergencia absoluta o condicionada. Incluso se pueden añadir variables espacialmente ponderadas. En el presente trabajo vamos a usar datos de corte transversal para analizar la convergencia absoluta por medio de estimaciones lineales. El modelo adopta la siguiente forma:
donde gi, T es el cambio en puntos porcentuales4 de las necesidades básicas insatisfechas (nuestra variable proxy de pobreza) para el municipio i durante el horizonte temporal T5, NBIi,0 es el valor de las necesidades básicas insatisfechas para el municipio i en el periodo inicial, si es el término de error o perturbación estocástica, del cual se asume que cumple todos los supuestos y condiciones necesarias de una regresión clásica.
Ahora bien, el objetivo de la regresión consiste en calcular el valor del coeficiente β y su significancia estadística. Se dice que existe convergencia en la variable gi, T si el signo del coeficiente β es negativo. Mientras más cercano a -1 significa que a mayores niveles de NBI mayor será la reducción en este indicador de pobreza y, por lo tanto, mayor será la convergencia. La existencia de convergencia implica que aquellos municipios con más necesidades básicas insatisfechas tenderán a satisfacer estas necesidades a un ritmo más rápido que los municipios con menos necesidades básicas insatisfechas lo que reducirá la brecha entre ambos grupos hasta eventualmente converger.
Si, por el contrario, el valor de β es positivo, entonces se observa divergencia, lo que significa que la brecha entre ambos grupos (los municipios pobres y los ricos) se amplía. En otras palabras, los municipios con más necesidades básicas insatisfechas tenderán a satisfacer estas necesidades a un ritmo más lento que aquellos municipios con menos necesidades básicas insatisfechas.
Una tercera opción podrá ser que el valor de β no sea estadísticamente distinto de cero. En este caso no existe divergencia, ni convergencia. Una posible ex plicación para este resultado es la existencia de "clubes" de convergencia. Esto significa que podría haber municipios con estructuras y dinámicas similares entre ellos, pero muy distintas al resto, por lo que tenderán a un estado estacio nario diferente (de ahí el término "club").
Existen distintas formas de modelar los clubes de convergencia. En nuestro caso vamos a favorecer la parsimonia de nuestro modelo sin arriesgar los gra dos de libertad por lo que se incluirán variables dicótomas para controlar cier tos clubes que se han detectado a partir de una inspección detallada de los datos. En este caso la ecuación 1 quedará de la siguiente manera:
donde la única diferencia viene dada por la inclusión de la variable dummy (dicótoma), la cual se usará para "controlar" ciertos municipios que presentan valores atípicos o que tienen alguna característica en común que permite agru parlos como parte de algún club. Las definiciones concretas se las verá en la siguiente sección.
3.2. Datos
Como se explicó en la anterior sección, nuestro análisis se basa en datos de corte transversal. Los datos de Necesidades Básicas Insatisfechas se obtuvieron del Instituto Nacional de Estadística (INE) y de la Unidad de Análisis de Políticas Sociales y Económicas (UDAPE) correspondientes a tres periodos que concuerdan con los censos de los años 1992, 2001 y 2012. Resulta importante indicar que el índice de NBI se mide como porcentaje de la población, vale decir, se sitúa entre 0 (0 %) y 100 (100 %). Un índice cercano a 100 significa que existe una mayor proporción de personas con necesidades básicas que no han sido satisfechas en el municipio, mientras que un índice cercano a 0 significa que las necesidades básicas han sido satisfechas para la mayoría de la población.
Antes de continuar, es importante dejar en claro que idealmente los datos de PIB a nivel municipal hubiesen sido la mejor opción para proceder a un aná lisis de convergencia beta. Sin embargo, hasta donde se conoce, ni el INE ni UDAPE han recolectado suficientes datos sobre PIB municipal como para permitirnos realizar un análisis de esta magnitud. Aun así, creemos que el uso del índice NBI se plantea como una buena aproximación para la pobreza estructural, la que además comporta la ventaja de no estar sujeta a los vaivenes de las fluctuaciones económicas de corto plazo, y, por tanto, se adecua correctamente al marco conceptual de convergencia6. De hecho, la intuición en este caso sobre el mecanismo subyacente para alcanzar el proceso de convergencia es muy clara, lo que equivale a decir que los municipios con mayor pobreza y por tanto con mayor proporción de población con necesidades básicas insatisfechas tenderán a usar sus recursos de forma casi exclusiva para cubrir estas necesidades básicas apremiantes. En contraste, un municipio con menor proporción de la población con necesidades básicas insatisfechas, puede moverse en su escala de necesidades, por lo que muy probablemente destinará sus recursos a otros fines. Eventualmente, los municipios con mayor pobreza, al destinar mayor cantidad de recursos -porcentualmente con respecto al total- tenderán a acortar la brecha en relación a los municipios que inicialmente tenían menor índice de NBI.
Finalmente, tal y como se mencionó en la introducción, una característica de nuestros datos es que cubren todo el periodo de la Participación Popular. Por lo tanto, nos permiten analizar qué ha sucedido con las NBI, desde la vigencia de la ley hasta su abrogación. Básicamente, contamos con los insumos suficientes para analizar si a partir de la PP los municipios con mayor NBI han podido igualar a aquellos municipios con menos NBI, o si, por el contrario, las diferencias han aumentado.
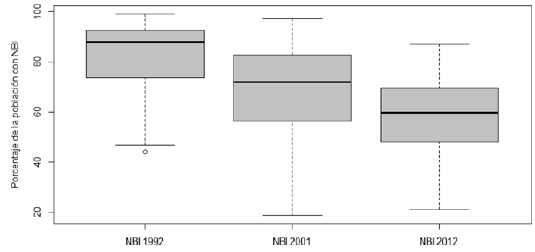
El cuadro 1 presenta las estadísticas descriptivas de nuestra variable de interés para los tres periodos. Lo primero que resulta evidente es que el número de observaciones aumenta a partir del año 2001 con la creación de nueve nuevos municipios7. Más importante aún, tanto el valor promedio -x como la mediana ex disminuyen a medida que pasa el tiempo, lo que indica una mejora general en la satisfacción de necesidades básicas. Pero lo que más llama la atención es la concentración de los datos en torno a valores altos (ver figura 1) así como la ampliación del rango. Por ejemplo, para el año 1992 el 50% de los datos evidenciaba un índice NBI igual o mayor a 88.1, es decir, en la mitad de los municipios la proporción de habitantes con necesidades básicas insatisfe chas era igual o mayor al 88.1%. Por otro lado, el rango, vale decir, la diferencia entre el valor mínimo y el valor máximo para el año 1992 era de 54.9 puntos porcentuales, mientras que diez años después se amplía a 78.3, dando señales de divergencia en lugar de convergencia.
4. Resultados
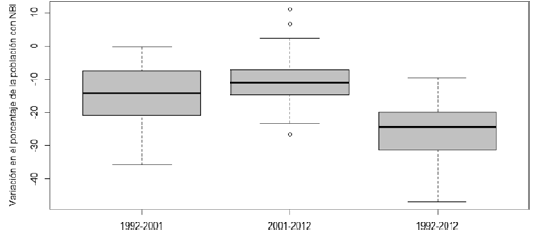
En esta sección analizamos los resultados de estimar las ecuaciones 1 y 2. Dado que el cambio en NBI se usa como variable dependiente, lo primero que vamos a hacer es la transformación de esta variable. La figura 2 muestra el diagrama de caja de la variable transformada, en otros términos, de la diferencia de NBI entre un periodo y otro. Como es de esperarse, tanto la concentración como el rango disminuyen.
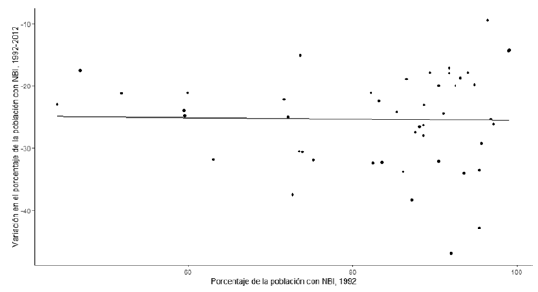
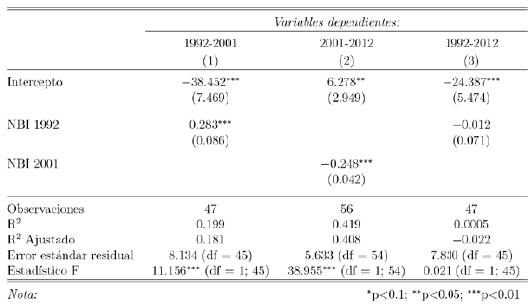
La figura 3 muestra el gráfico de dispersión para los datos de las variables dependiente e independiente de la regresión 1 en el periodo 1992-2012. El ajuste de la curva de regresión se presenta ligeramente negativo, pero no parece ser lo suficiente como para garantizar sólidamente la existencia de convergencia. Los resultados del cuadro 2 confirman nuestras sospechas, no existe convergencia. El coeficiente beta, aunque negativo (-0.012), no es estadísticamente distinto de cero. En otras palabras, para el periodo 1992-2012 no se observa que los municipios con mayor NBI hubiesen mejorado sus condiciones lo suficiente como para poder eventualmente "alcanzar" a los municipios con menor NBI. Este resultado es en cierto modo intrigante, dado el objeto y alcance de la ley de PP que estuvo vigente precisamente durante este periodo de estudio.
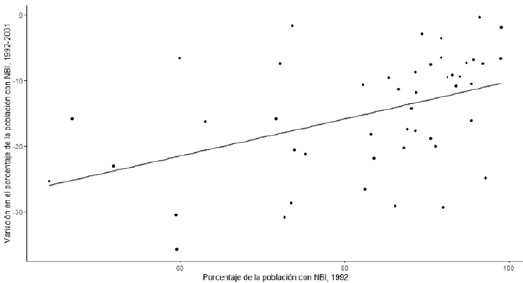
A fin de entender mejor el proceso de convergencia, se decidió dividir los datos en dos periodos. El primero que abarca el subperiodo 1992-2001 y el segundo, el subperiodo 2001-2012. La figura 4 muestra el gráfico de dispersión para las variables dependientes e independientes en el periodo 1992-2001. El resultado es aún más desconcertante que el analizado para todo el periodo en su conjunto. En este caso, no solamente no existe convergencia, sino que además existe divergencia (la pendiente de la curva de ajuste es positiva).
Los resultados en la primera columna del cuadro 2 ilustran que el coeficiente beta es positivo (0.283) y estadísticamente significativo, lo que corrobora el proceso de divergencia observado en la figura 4. Este resultado significa que la brecha existente entre los municipios con baja cobertura con respecto a aquellos con amplia cobertura de las necesidades básicas se ha incrementado. Los datos del cuadro 1 ya nos daban señales de la lentitud de ajustes del último con respecto al primer cuartil y nuestros resultados lo confirman.
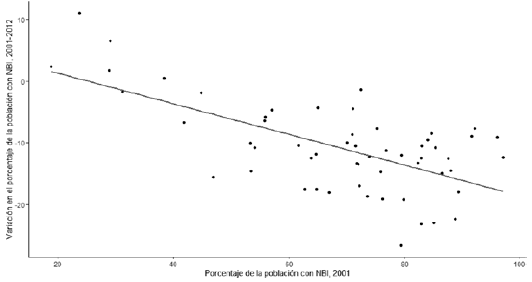
En la figura 5 se aprecia el gráfico de dispersión de nuestras variables de interés para el subperiodo 2001-2012. A primera vista se observa una sólida pendiente negativa, lo que es un claro indicio de convergencia. La segunda columna del cuadro 2 da cuenta de un coeficiente negativo (-0.248) y estadísticamente significativo, lo que ratifica el hallazgo de convergencia para este periodo.
En suma, no se encuentra evidencia sólida de convergencia beta en el índice de las necesidades básicas insatisfechas para los municipios de Santa Cruz durante el periodo 1992-2012. Si acaso, se puede observar un ínfimo proceso de convergencia, pero estadísticamente no significativo. Sin embargo, se pueden claramente distinguir dos subperiodos. El primero que se localiza entre 1992-2001, en el cual se encuentra divergencia, y el segundo que abarca el periodo situado entre 2001-2012, cuando se encuentra convergencia.
4.1. Análisis de robustez
El cuadro 3 muestra los resultados de estimar la ecuación 1 con errores estándares robustos. Se puede observar que la significancia estadística de nuestros coeficientes beta no cambia, por lo que el análisis de la sección anterior continúa siendo válido.
Siguiendo con el análisis de robustez, estimamos la ecuación 2 con distintas definiciones de variables dicotómicas. Al igual que antes, lo que nos interesa es el coeficiente beta, pero adicionalmente el signo y la significancia estadística de la variable dummy. Antes de ver los resultados, se hace imprescindible explicar nuestras cuatro categorías de variables dummies, lo cual hacemos a continuación.
Aunque todos los municipios mejoraron en la satisfacción de las necesidades básicas durante el periodo 1992-2012, se presentan ciertos municipios cuya mejora fue insignificante. Por ejemplo, el municipio Gutiérrez es el que menor cambio ha registrado en su índice NBI. Los datos exponen que ha pasado de tener un índice de 96.4 en 1992 a 87 en 2012; vale decir, una mejora de apenas 9.4 puntos porcentuales8 en su índice de necesidades básicas insatisfechas. Le siguen Urubichá, El Puente y Cuevo. Lo interesante es que Gutiérrez y Cuevo están en la provincia Cordillera, mientras que Urubichá y El Puente se ubican en la provincia Guarayos9; por tanto, creamos una dummy para los municipios de ambas provincias.
En el otro extremo destacan los municipios de las provincias Vallegrande y Florida, que casi sin excepción se encuentran entre los que más disminuyeron su NBI (o sea, ampliaron la cobertura de necesidades básicas durante el periodo de estudio). De hecho, el municipio El Trigal (provincia Vallegrande) es el que mejoró en mayor proporción, pasando de 92 en 1992 a 45 en 2012. A diferencia de las provincias Cordillera y Guarayos que no son vecinos, las provincias Vallegrande y Florida sí tienen una frontera en común, por tanto, decidimos unirlas en un solo grupo con el nombre de Valles, ya que podría existir algún factor común a todos los municipios de estas dos provincias. Finalmente, la dummy Metrópolis se refiere a los municipios aledaños al municipio de Santa Cruz de la Sierra, siendo muy probable que exista un efecto goteo dada la cercanía con el municipio más grande y poblado del país.
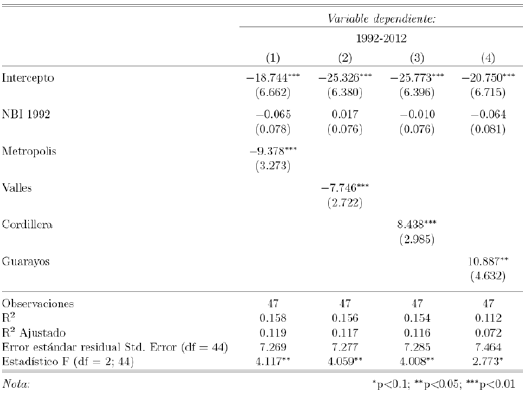
El Cuadro 4 muestra los resultados de estimar la ecuación 2 empleando los distintos tipos de variables dummies explicadas en el párrafo anterior. Dos observaciones que se deben hacer. Primero, el coeficiente beta sigue siendo en su mayor parte negativo excepto para la regresión de los valles; sin embargo, en todos los casos es estadísticamente no significativo, por lo que confirma nuestros resultados obtenidos y relativos al coeficiente beta en la ecuación 1 para el mismo periodo. Segundo, todas las variables dummies son estadísticamente significativas. Esto podría estar indicando la existencia de clubes de convergencia o algún tipo de shock idiosincrático en esos municipios.
4.2. ¿Convergencia o divergencia?
Los resultados obtenidos hasta ahora parecerían ser contradictorios. Durante la primera mitad del periodo se tuvo divergencia, mientras que durante la segunda mitad, convergencia. Para empeorar las cosas, durante el periodo total no se observa evidencia estadística de convergencia ni de divergencia, a lo mucho un débil coeficiente negativo. ¿A qué se debe este resultado aparentemente tan extraño? Aunque somos conscientes de las limitaciones de nuestra investigación y de sus objetivos, creemos importante hipotetizar sobre las posibles causas de estos curiosos resultados, no sin antes dejar en claro que las posibles causas no son únicas ni excluyentes.
Periodo 1992-2001
Este constituye el periodo en el que se observa divergencia, vale decir, los municipios que, con un -relativamente- buen indicador NBI, mejoraron más que los municipios con -malos- indicadores NBI. Esto provocó que la brecha de cobertura de necesidades básicas se agrande. Precisamente durante este periodo (específicamente en el año 1994), entra en vigencia la ley de PP, y aunque la ley tenía por objeto mejorar la calidad de vida de los ciudadanos10 e incluso transfería infraestructura física de deporte, salud, micro-riego, y educación del gobierno central a los municipios, esto no fue suficiente para minimizar la diferencia existente entre aquellos municipios que podían cubrir sus necesidades básicas y aquellos que no. De hecho, creemos que la forma como fue concebida la ley de PP acrecentó esta diferencia.
Esto se podría deber a dos motivos. Según la ley de PP, por lo menos 90% de los recursos de coparticipación tributaria para la Participación Popular deberían asignarse a inversión pública. El problema radica en que la definición de inversión pública es muy vaga, por lo que la misma no precisamente tiene que dirigirse a aquellos sectores relacionados con la cobertura de necesidades básicas (salud, educación, acceso a electricidad e infraestructura de vivienda), y por el mismo hecho se deja mucho espacio de maniobra para políticas discrecionales. Segundo, los recursos eran asignados sobre la base de la población. Los municipios más pequeños -en términos poblacionales- recibirían menos recursos,11 por lo que difícilmente podrían beneficiarse de economías a escalas en la construcción de infraestructura básica, lo que resultaría en otro tipo de gasto que se ajustara a los ingresos, pero no necesariamente enfocado en cubrir los requerimientos básicos. En este sentido, el tipo de gasto es de suma importancia como demuestran los trabajos de Montero Kuscevic (2012) así como de Escobar, Chalup y Alarcón (2021).
Periodo 2001-2012
Aunque en este periodo la ley de PP seguía vigente, hacia el año 2005 se generó un cambio esencial al aprobarse la Ley de Impuestos Directos a los Hidrocarburos, la misma que, a diferencia de la ley de PP, indicaba de forma explícita que los recursos debían usarse exclusivamente para aquellas áreas relacionadas con necesidades básicas, como ser salud, educación y caminos.
Periodo 1992-2012
El resultado para el periodo 1992-2012 resulta menos sorpresivo una vez que se han analizado los dos subperiodos. El cambio en la tendencia inicial de divergencia hacia convergencia parece estar fielmente capturado en el irrisorio y estadísticamente no significativo valor del coeficiente beta. Sin embargo, el resultado negativo parece indicar que el efecto IDH pesa más que el efecto PP.
5. Conclusiones
Este trabajo analiza el proceso de convergencia en los municipios de Santa Cruz durante el periodo 1992-2012, usando el Índice de Necesidades Básicas Insatisfechas como variable proxy para la pobreza. Tendiente a las estimaciones se emplearon datos de corte transversal y mínimos cuadrados ordinarios.
Los resultados para el subperiodo 1992-2001 muestran un indiscutible proceso de divergencia que la descentralización de recursos producida a partir de la ley de Participación Popular no modificó. En cambio, referido al subperiodo 2001-2012 se encuentra clara evidencia de un proceso de convergencia, posiblemente influenciado por la descentralización y gran magnitud de recursos condicionados a inversiones específicas, generados a partir de la ley de Impuestos Directos a los Hidrocarburos. Para el periodo total 1992-2012 nuestros resultados muestran un ligero indicio de convergencia, aunque el coeficiente es estadísticamente no significativo lo que podría explicarse por el cambio observado en la tendencia durante ambos subperiodos.
Finalmente, se pudieron identificar ciertos clubes de convergencia, primero, en la zona de los valles, el área metropolitana del municipio de Santa Cruz de la Sierra, los cuales logran disminuir en gran magnitud su proporción de personas con necesidades básicas insatisfechas. También, en los municipios de las provincias Guarayo y Cordillera, los cuales, a su vez, presentan cambios pequeños en su índice NBI durante el periodo analizado.
Aunque nuestros resultados constituyen una primera aproximación al tema de convergencia municipal, creemos que sería interesante extender el análisis para abarcar todos los municipios del país. Además, se plantea la oportunidad de realizar un análisis de convergencia condicionada con la inclusión de variables adicionales a fin de controlar las diferentes estructuras de los municipios.