Artículos y Estudios

 

UN ENFOQUE PARA LA ACOTACIÓN DEL ERROR EN LOS MÉTODOS ITERATIVOS

 

 

José Gil Iñiguez

José Gil Iñiguez, realizó estudios en la Universidad Nacional de la Plata habiendo obtenido el título de licenciado en Informática;cursos de postgrado en tópicos de matemática aplicada y sistemas de información en la Universidad de Buenos Aires, de investigación operativa y análisis numérico en la Universidad Nacional de la Plata, de matemática pura en la Universidad de Stanford (EE.UU). Fue Jefe del Departamento de Matemática en la Facultad de Ciencias Puras de la UMSA; ex profesor en la misma Universidad; catedrático en la Escuela Militar de Ingeniería (EMI) y profesor de la Escuela de Guerra Naval. En la Universidad Católica Boliviana ocupa actualmente los cargos de Director de la Carrera de Ingeniería de Sistemas y del Centro de Cómputo, además de dictar varios cursos tanto en su Carrera como en Economía.

 

 

---

Para la resolución del sistema Ax = b, los métodos más eficientes y de aplicación general, son los de eliminación (métodos directos). Sin embargo existe una categoría muy vasta de problemas relacionados especialmente con la resolución numérica de ecuaciones diferenciales parciales, en los que la matriz A se caracteriza por tener un gran número de elementos nulos, en ese caso se justifica el uso de métodos iterativos de los que describiremos los más importantes.

MÉTODOS DE JACOBI Y GAUSS - SIEDEL:

Sea el sistema Ax = b (1), consideremos la matriz A como suma de una matriz diagonal D, una triangular inferior L y otra triangular superior U.

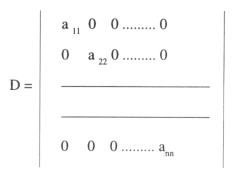
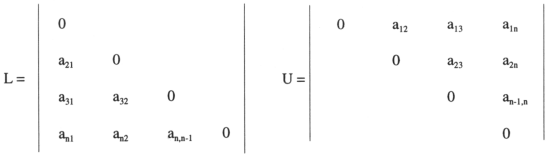
Es decir A = D + L + U

El sistema (1) se puede escribir en la forma equivalente:

o bien:

que sugiere la fórmula iterativa:

k = 0, 1,2,.......

esta fórmula define el proceso de Jacobi, también llamado método de los desplazamientos simultáneos.

Desarrollando (4), obtenemos:

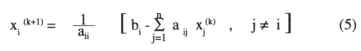
k = 0, 1, 2,.......

i = 1, 2, 3.....n

que observándola, vemos que en cada ciclo iterativo se calculan aproximaciones para todas las incógnitas usando solamente aproximaciones del ciclo anterior.

En el método de Gauss - Seidel o de los desplazamientos sucesivos cada ciclo iterativo comprende las siguientes operaciones. Haciendo i = 1 en (5) se obtiene:

esta aproximación de x₁, se usa en la aproximación de x₂, o sea:

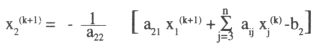
y así sucesivamente, teniendo en forma general:

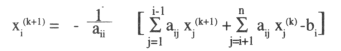
k = 0, 1, 2,.......

i = 1, 2, 3,... ,n

esta fórmula iterativa es equivalente a la ecuación matricial:

que a su vez es equivalente a:

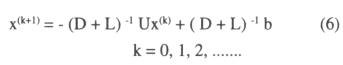
fórmula que define el método de Gauss - Seidel.

 

CONVERGENCIA Y ACOTACIÓN DEL ERROR DE TRUNCAMIENTO:

Las fórmulas (4) y (6) se pueden escribir en la forma general:

donde:

El error de truncamiento en la k-ésima iteración será:

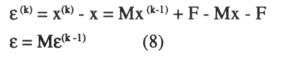
y repitiendo este proceso se llega a:

para cualquiera sea el error inicial .

Tomando normas:

El método será convergente cuando:

que es lo mismo que:

condición que se cumplirá cuando:

Sabemos por otro lado que:

o sea que el método será convergente cuando:

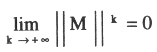
para que se cumpla esto es suficiente que || M || < 1, ó según alguna proposición anterior | t_i | < 1 para todo i, donde los t_i son autovalores de M.

Nos falta ahora encontrar, de alguna manera, la cota superior del error, para esto llamaremos:

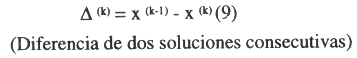
será luego:

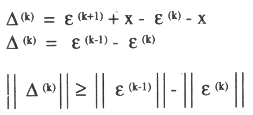
y de acuerdo a (8):