Probando la condición Marshall-Lerner y Curva-J para el Perú: un análisis de cointegración multivariada

 

Testing for Marshall-Lerner Condition and J-Curve from Peru: An analysis of multivariate cointegration

 

 

Luis Francisco Laurente Blanco*, Dan Manuel Machaca Ticona**

 

 

---

Resumen

En el Perú, la balanza comercial ha jugado un papel protagónico en el desempeño económico, particularmente a partir del año 2002, en que empieza a registrar superávits. Es así que para el año 2018 se registró un superávit de US$ 7,049 millones. Este dinamismo del comercio internacional mantiene al comercio exterior como uno de los principales motores de la economía peruana. El objetivo del estudio es probar la condición Marshall-Lerner y la Curva-J para el Perú utilizando información mensual de los años 2000 a 2018 obtenida del Banco Central de Reserva del Perú (BCRP). Para el análisis se emplea la metodología de Johansen-Juselius y el Modelo Vector de Corrección de Error (MVCE). Los resultados revelaron el cumplimiento de la condición Marshall-Lerner para el largo plazo y, haciendo uso de los diagramas de impulso-respuesta, se confirma que no se cumple el fenómeno de la Curva-J en la economía peruana.

Palabras clave: VAR, cointegración, modelo vector de corrección de error, balanza comercial, tipo de cambio real.

---

Abstract

In Peru, the trade balance has played a leading role in economic performance, particularly since 2002, when it began to record surpluses, so that by 2018 there was a surplus of US$ 7,049 million. This dynamism of international trade keeps foreign trade as one of the main engines of the Peruvian economy. The objective of the study is to prove the Marshall-Lerner condition and the J-Curve for Peru using monthly information from the years 2000 to 2018 obtained from the Central Reserve Bank of Peru (BCRP). For the analysis, the Johansen-Juselius methodology and the Error Correction Vector Model (MVCE) are used. The results revealed the compliance of the Marshall-Lerner condition for the long term and, by making use of impulse response diagrams, it is confirmed that the phenomenon of the J-Curve in the Peruvian economy is not fulfilled.

Keywords: VAR, cointegration, vector error correction model, trade balance, real exchange rate.

Clasificación/Classification JEL: C32, C51, F41

---

 

 

1. Introducción

El Perú siempre ha sido un exportador de productos primarios y un importador de productos manufacturados, y al igual que muchos países en el mundo, ha experimentado ciclos de crisis y recuperación, generalmente ligados a fluctuaciones en el mercado internacional, como la crisis financiera de 2008 en EEUU y Europa y el shock de 2015 (Velazco y Pinilla, 2017) que tuvieron un impacto sobre la economía peruana, especialmente por las exportaciones que realiza. Sin embargo, el Perú mostro una evidente recuperación. Las exportaciones peruanas se basan principalmente en 829 productos que registran un record de crecimiento, evidenciando calidad, competitividad y diversificación, en un crecimiento histórico en 45 mercados, y revelando la importancia de los diversos tratados de libre comercio que realizó el país con importantes economías en el mundo (ADEX, 2019). Esto ha traído como resultado un incremento de las exportaciones en las últimas décadas.

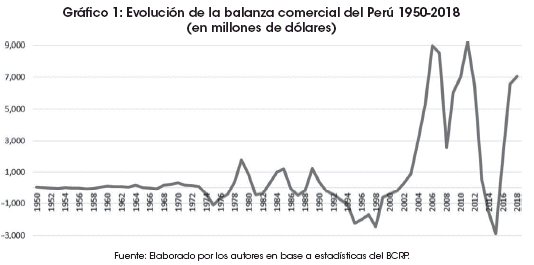
Es así que las exportaciones en el año 2018 llegaron a US$ 48,942 millones, lo que representa el 29% del PBI del Perú (BCRP, 2018). Como resultado, la balanza comercial ha jugado un papel protagónico en el desempeño económico. Particularmente, a partir del año 2002, año en que empieza a registrar superávits, los cuales han alcanzado un record histórico de US$ 8,986 millones para 2006, US$ 8,503 millones para 2007, US$ 2,569 millones para 2008, llegando a US$ 7,049 millones en el año 2018. Este dinamismo que ha impregnado el comercio internacional en términos de diversificación de producción de mercados de destino y de generación de empleo, mantiene al comercio exterior como uno de los principales motores de la economía peruana (Bustamante y Morales, 2009). El Gráfico 1 muestra la evolución de la balanza comercial del Perú desde el año 1950 hasta 2018, exhibiendo un comportamiento creciente a partir del año 2002.

Dado este contexto, cabe preguntarse acerca del comportamiento de tales cuentas en relación con uno de sus principales determinantes: el tipo de cambio real. En general se suele argumentar que las depreciaciones reales son expansivas en tanto favorecen la competitividad internacional e incrementan las exportaciones netas. Esta dinámica se basa en la condición de Marshall-Lerner, la cual expresa que una depreciación del tipo de cambio real mejora la balanza comercial siempre y cuando la suma de las elasticidades de la demanda por importaciones y la demanda por exportaciones sea mayor a la unidad. No obstante, evidencia empírica ha mostrado que aun satisfaciendo la condición Marshall-Lerner, una depreciación del tipo de cambio real puede conducir al deterioro temporal de la balanza comercial, seguido más delante por una mejora de la misma. En ese caso, una depreciación cambiaria precipita una trayectoria en forma de J de la balanza comercial, con un deterioro inicial seguido de una recuperación consistente con Marshall-Lerner (Sastre, 2010). Finalmente, poner atención en las variables macroeconómicas como la balanza comercial, el tipo de cambio real, el ingreso y la demanda extranjera es de gran importancia para el desarrollo de políticas, en particular en economías pequeñas y abiertas al mundo como el Perú.

El objetivo principal de esta investigación es verificar el cumplimiento de la condición Marshall-Lerner y la Curva-J para la economía peruana en el período 2000-2018. Al respecto se mencionan algunos estudios relacionados: a nivel internacional existe un número de trabajos que verifican el cumplimiento de la condición Marshall-Lerner (Lerner, 1944) y la Curva-J; entre ellos se tiene los trabajos de Sadok (2018), Cambazoglu y Gunes (2016), Chena y Bosnic (2017), Backus et al. (2007), Onakoya yJohnson (2018), Pandey (2013), Siklar y Celik (2018), Eita y Africa (2013) y Krzyzanowski (2017). En particular, Ali, Nafees y Farid (2017), en su estudio sobre la condición de Marshall-Lerner para los países del sur de Asia, utilizan el modelo de efecto aleatorio (REM), la especificación de Hausman y el test de Breusch-Pagan para estimar las elasticidades de demanda de exportaciones e importaciones, encontrando que la condición no se cumple. Arriaga y Landa (2016) usan el Modelo Vector de Corrección de Error (MVCE) y concluyen que el tipo de cambio real empeora la balanza comercial, lo que indica el cumplimiento de la Curva-J en el corto plazo. Türkay (2014) aplica la metodología de Johansen y el Modelo de Corrección de Error (MVCE), y los resultados de la estimación de las funciones de demanda de exportación e importación respaldan el cumplimiento de la condición de Marshall-Lerner, debido a que la elasticidad de las demandas de exportación e importación es superior a la unidad. Schaling y Kabundi (2014) utilizan la metodología de Modelo Vector de Corrección de Error, encontrando evidencia de la existencia del efecto de la Curva-J. Abd-El-Kader (2013) emplea la metodología ARDL, y muestra que existe una relación de largo plazo entre la balanza comercial, el tipo de cambio real bilateral, el producto bruto interno y la producción extranjera para diversos países, hallando evidencia del cumplimiento de la condición de Marshall-Lerner y el efecto de la Curva-J. Lal y Lowinger (2012), en su investigación sobre la Curva-J en Asia, demostraron que el tipo de cambio real tiene un efecto sobre la balanza comercial en los países analizados; asimismo, utilizando la función de impulso-respuesta, prueban la existencia del fenómeno de la Curva-J.

Al respecto, Bravo (2009) utiliza la metodología de mínimos cuadrados, confirmando el cumplimiento de la condición Marshall-Lerner; luego, hace uso de la metodología de corrección de error para verificar el cumplimiento de la Curva-J. Sastre (2005) usa un modelo biecuacional simultáneo cointegrado para comprobar la condición Marshall-Lerner y la Curva-J; Sek y Har (2014) emplean la metodología de mínimos cuadrados y mínimos cuadrados completos, demostrando la validez de la hipótesis de Marshall-Lerner. Asimismo, los trabajos de Ardila, Mora y Cuevas (2018) y Beltrán (2016) corroboran la condición de Marshall-Lerner para los sectores de alimentos, agricultura, minería y manufactura, encontrando que la depreciación real no conlleva a una mejora en la balanza comercial en estos sectores. Para el caso peruano se tiene el trabajo de Bustamante y Morales (2009), quienes prueban que la Curva-J no está presente en la economía peruana; sin embargo, se cumple la condición Marshall-Lerner para el largo plazo.

El resto del documento se organiza de la siguiente manera: en la sección 2 se explica la metodología econométrica empleada, en la sección 3 se realiza la especificación del modelo a estimar, en la sección 4 se muestran los resultados, y finalmente, en la sección 5, se presentan las conclusiones más sobresalientes del presente estudio.

 

2. Metodología

El primer paso en la presentación de la metodología es determinar las variables a ser utilizadas y verificar si son estacionarias o no estacionarias. Para tal fin se utilizan los tests estadísticos ADF propuestos por Dickey y Fuller (1979) y el test PP propuesto por Phillips y Perron (1988). Si los estadísticos ADF y PP calculados son mayores que los valores críticos, entonces se dice que la variable económica X es estacionaria o integrada de orden cero, i.e., I(0); caso contrario, se realizan los tests de ADF y PP en primera diferencia para conseguir que la variable X sea estacionaria, i.e., ΔX; para este caso la variable económica se dice que es integrada de orden uno I(1).

Si todas las variables económicas son integradas de orden uno, es decir I(1), entonces el siguiente paso (llamado también cointegración) es encontrar evidencia de una relación de largo plazo usando la metodología de Johansen¹. La metodología de cointegración se presenta en las siguientes líneas:

Considere un modelo VAR con k retardos en el proceso X, definido por:

donde ε_t es el término de error Gausiano p-dimensional con media cero y matriz de varianza Δ, X_t es un vector de variables I(1) y μ es un vector de constantes. Debido a que X_t es no estacionaria, la ecuación (1) puede ser expresada en un modelo de corrección de error en primeras diferencias:

donde Γ_i = -(I-Π₁-...-Π_i), i = 1, 2,..., k-1 y Π = -(I-Π₁-...-Π_k).

La matriz de coeficientes Π contiene información respecto del largo plazo entre las variables en el vector de base de datos. Si el rango de Π es igual a p, es decir que la matriz tiene rango completo, el vector X_t es estacionario. Si el rango de Π es igual a cero, la matriz es una matriz nula y la ecuación (2) corresponde a un vector de series de tiempo diferenciado. Finalmente, si 0<r<p, existen r vectores de cointegración; en el caso Π = αβ' donde α y β tienen la propiedad de que β'X_t es estacionaria, la ecuación (2) se interpreta como un Modelo Vector de Corrección de Error (MVCE).

Johansen (1988) y Johansen y Juselius (1990) derivaron el test para la hipótesis de r vectores de cointegración o Π = αβ'. El rango de cointegración, r, puede ser testeado con dos estadísticos denominados trace y máximo eigenvalue.

El test estadístico de trace para la hipótesis nula, que existen como máximo r vectores de cointegración, es calculado como:

donde _r+1,...,_p son p - r eigenvalores estimados. Por otro lado, el test de máximo eigenvalue para la hipótesis nula de r vectores de cointegración, está dado por

Ambos tests sugieren cointegración en presencia o ausencia de componentes determinísticos en el modelo dinámico.

 

3. Especificación del modelo

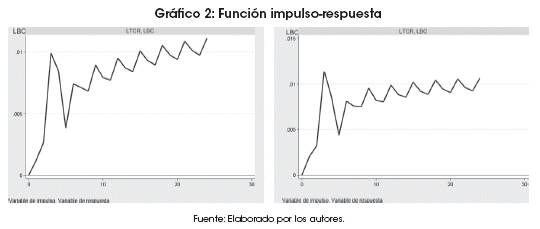
El modelo teórico para la relación entre el tipo de cambio y la balanza comercial se discute en varios documentos y artículos. En esta sección se sigue la discusión de Caporale y Gil-Alana (2012). Se define al tipo de cambio real, E_t, como el nivel de precios extranjero, P_t* , multiplicado por el tipo de cambio nominal, S_t, y dividido por el nivel de precios de la economía local, P_t,

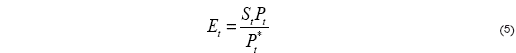
Por otro lado, se puede definir a la balanza comercial como el cociente entre las exportaciones totales y las importaciones totales:

donde las exportaciones totales se obtienen multiplicando el nivel de exportaciones por el precio extranjero, y las importaciones totales como el volumen de importaciones por el tipo de cambio. Tomando logaritmos en la ecuación (6) se tiene la siguiente ecuación:

Se definen las funciones de demanda de exportaciones e importaciones del largo plazo en logaritmos en las ecuaciones (8) y (9), escritas a continuación:

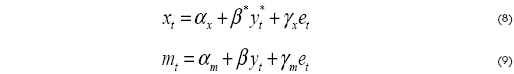
donde y_t* y y_t son los ingresos del país extranjero y del país doméstico, respectivamente; los parámetros γ_x y γ_m son las elasticidades de las exportaciones e importaciones, respectivamente, y la variable e_t = S_t — p_t + p_t* representa al tipo de cambio real en logaritmos. Reemplazando las ecuaciones (8) y (9) dentro de la ecuación (7) se tiene la ecuación del largo plazo de la balanza comercial:

La condición de Marshall-Lerner establece que una depreciación del tipo de cambio real (TCR) incrementa el nivel de las exportaciones. Para que se cumpla esta condición, es necesario que la ecuación (1 0) verifique lo siguiente:

Luego, en su forma empírica, la ecuación (10) queda determinada de la siguiente manera:

Y además se plantea la ecuación (10) aumentada por los términos de intercambio para evaluar la condición Marshall-Lerner, dada por

donde la variable LBC_t representa el logaritmo de la balanza comercial, expresada como el cociente entre las exportaciones e importaciones peruanas en el período t, i.e. LBC_t = ln(X_t/M_t), donde X_t son las exportaciones peruanas en el período t y M_t las importaciones totales en el período t. La variable LTCR_t representa al logaritmo del tipo de cambio real del Perú en el período t. El tipo de cambio real es utilizado como el proxy del índice del tipo de cambio real bilateral (2009=100). La variable LPBI_t indica el logaritmo del producto bruto interno del Perú en el período t, dado por el producto bruto interno por tipo de gasto en millones de soles. De la misma forma, la variable LPBIE_t representa al logaritmo de la producción bruta extranjera en el período t calculado como proxy de la demanda total de los principales socios comerciales del Perú expresado en millones de dólares y convertido a soles por el tipo de cambio nominal sol/dólar. La variable LTI_t es el logaritmo de los términos de intercambio en el período t, estimado como proxy de la evolución del precio de los productos exportados, calculado según el valor de los productos importados. Los valores α_j, β_i (j=0,1,...,3,i=0,1,...,4) son parámetros de los modelos planteados, y el término ε_t representa al término de error en el período t, que se considera que se distribuye con una Normal estándar.

Para el cumplimiento de la condición Marshall-Lerner es necesario que los parámetros cumplan la desigualdad α₁ > 0 y β₁ > 0. Además, para mantener los efectos con el signo adecuado es necesario que los parámetros cumplan la desigualdad α₂,β₂ < 0, α₃, β₃ > 0 y β₄ < 0 . En efecto, los modelos a estimar para el contraste del cumplimiento de la condición de Marshall-Lerner serán el Modelo 1 y el Modelo 2.

 

4. Resultados empíricos

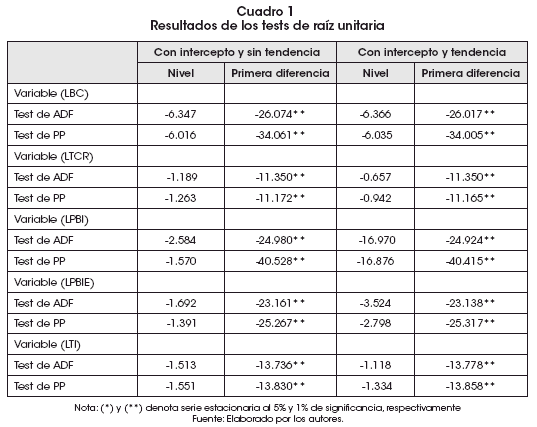
La información estadística para el presente estudio fue obtenida de la base de datos del Banco Central de Reserva del Perú (BCRP, 2018) con una frecuencia mensual para los años 2000 a 2018, haciendo un total de 228 observaciones. A continuación, se presentan los resultados de los modelos 1 y 2 dados por las ecuaciones (12) y (13) para verificar el cumplimiento de la condición Marshall-Lerner. Como primer paso para la estimación se determina el orden de integración de las variables macroeconómicas; para ello se utiliza el test de raíz unitaria ADF propuesto por Dickey y Fuller (1979), y el test P-P propuesto por Phillips y Perron (1988) que se muestran en el Cuadro 1. Los tests fueron calculados con intercepto sin tendencia, y con intercepto y tendencia. Se encontró que en niveles con intercepto y sin tendencia, las variables macroeconómicas balanza comercial (LBC), tipo de cambio real (LTCR), producto bruto interno peruano (LPBI), producción bruta extranjera (LPBIE) y los términos de intercambio (LTI) tienen una raíz unitaria bajo un contraste de 5% y 1 % de nivel de significancia estadística. De la misma forma, para el cálculo de estacionariedad de las variables se considera intercepto y tendencia, dando como resultado que todas las variables tienen raíz unitaria bajo un contraste de 5% y 1% de nivel de significancia estadística, lo que sugiere realizar el cálculo en primeras diferencias. Aplicando los tests de estacionariedad ADF y P-P en primera diferencia, se concluye que todas las series económicas descritas son estacionarias en primera diferencia, es decir, son I(1).

Para el contraste de especificación sobre el número óptimo de retardos k para el modelo VAR, se hace uso del criterio de información de Hannan-Quinn (HQIC), del criterio de información bayesiano de Schwarz (SBIC) y del Ratio Likelihood (LR), los cuales indican la utilización de cuatro retardos como el orden del VAR.

Test de cointegración de Johansen-Juselius

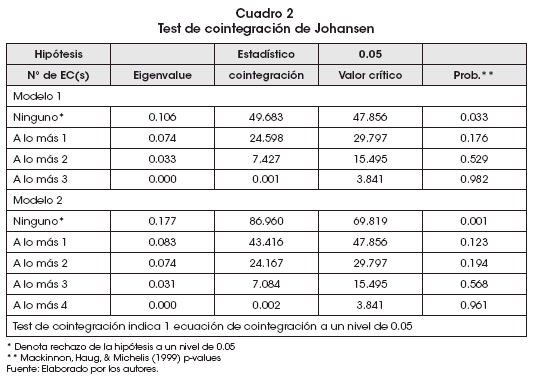
El test multivariado de Johansen-Juselius, propuesto por Johansen (1988) y Johansen y Juselius (1990), es utilizado para analizar las relaciones de cointegración entre las variables mediante los tests de la Trace y Max-Eigenvalue de cointegración. La estrategia de los tests empieza con la elección del modelo restrictivo y con la comparación del test estadístico con el valor crítico al 5% de significancia de la tabla de Mackinnon, Haug y Michelis (1 999), bajo la hipótesis nula de no existencia de cointegración (H₀: r =0). El Cuadro 2 muestra los resultados del test de cointegración de Johansen, que sugieren la existencia de una ecuación cointegrada a un nivel de 5% de significancia para ambos modelos planteados [(12) y (13)].

Para verificar la relación de causalidad unidireccional de las variables sobre la balanza comercial (LBC), se utiliza el test de causalidad de Granger propuesto por Granger (1980, 1988), definido con la hipótesis alterna (H) de causalidad unidireccional de una cierta variable X sobre Y. Los resultados indican que, para un nivel de significancia de 1%, las variables tipo de cambio real (LTCR), producto bruto interno (LPBI), demanda extranjera (LPBIE) y términos de intercambio (LTI) causan individualmente en el sentido de Granger a la balanza comercial (LBC); esta implicancia también se cumple de modo conjunto sobre la balanza comercial (LBC) a un nivel de significancia del 5%.

Modelo Vector de Corrección de Error (MVCE)

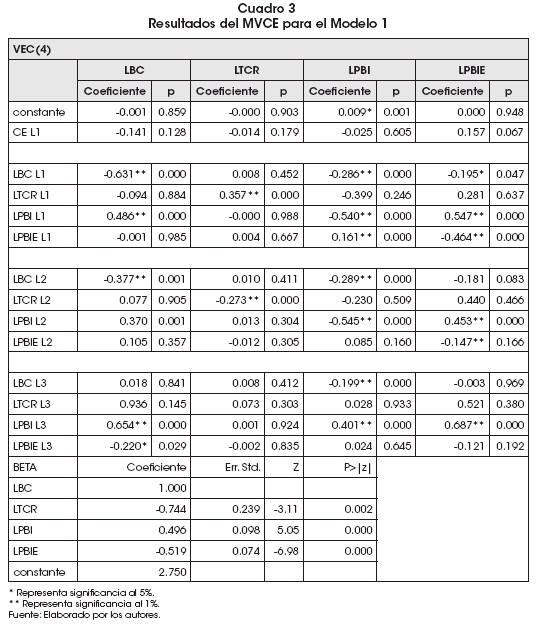
El Modelo Vector de Corrección de Error (MVCE) muestra la dinámica de corto plazo entre las variables y su relación con el largo plazo. Para ello es necesario que el coeficiente de corrección de error (representado por CE L1 del Cuadro 3) sea negativo, lo que indica que la serie es no explosiva en el tiempo y garantiza la existencia de equilibrio en el largo plazo del vector de cointegración. En esta sección se estimaron dos modelos de vector de corrección de error de los modelos (12) y (13), cuyos resultados se muestran en los Cuadros 3 y 4, respectivamente. Para el primer modelo, se observa en la primera columna (vector de LBC) que el coeficiente de corrección de error es igual a -0.141, manteniendo el signo negativo, lo que indica que el modelo MVCE para el Modelo 1 es no explosivo y que retorna al equilibrio de largo plazo. Es así que un porcentaje igual a 14.1% de los shocks existentes en el corto plazo sobre la balanza comercial son corregidos en el siguiente período. Esta velocidad de ajuste muestra que la balanza comercial en el Perú no es muy sensible a los shocks que impactan sobre el equilibrio de largo plazo.

Asimismo, el Cuadro 4 muestra el modelo vector de corrección de error para el Modelo 2, donde el coeficiente de corrección de error tiene un valor de -0.186 con signo negativo (primera columna), indicando que este sistema se encuentra en equilibrio y que los shocks existentes en el corto plazo sobre la balanza comercial son corregidos en el siguiente período.

Por otro lado, los Cuadros 3 y 4 muestran el vector de largo plazo de la Normalización de Johansen respecto a la balanza comercial (LBC), donde en ambos modelos los signos son los esperados y con significancia estadística en sus parámetros.

Condición Marshall-Lerner y Curva-J para la economía peruana

Para hallar los efectos de largo plazo y verificar el cumplimiento de la condición Marshall-Lerner para el caso peruano, se realiza la estimación a los modelos (12) y (13). Utilizando el Modelo Vector de Corrección de Error (MVCE) de los Cuadros 3 y 4 para evaluar los modelos a estimar, se presenta la ecuación de largo plazo mediante la Normalización de Johansen. Los resultados para el Modelo 1 son los siguientes:

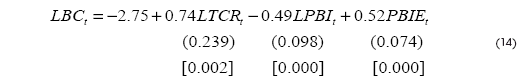
Los valores que se encuentran en paréntesis representan los errores estándar de los parámetros y los valores en corchetes representan los valores del estadístico P>|z| de probabilidad. En los resultados estimados se observa que los coeficientes de las variables guardan la relación esperada y que son estadísticamente significativos a un valor de 5% de significancia. Respecto al cumplimiento de la condición Marshall-Lerner, el parámetro que muestra el efecto del tipo de cambio real sobre la balanza comercial es mayor a cero, es decir

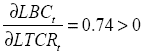
lo que indica que en el Perú, para el período 2000-2018, se cumple la condición Marshall-Lerner en el largo plazo, dada por la ecuación (12). De modo similar, estimando la ecuación (13) mediante la Normalización de Johansen, se tienen los resultados para el Modelo 2:

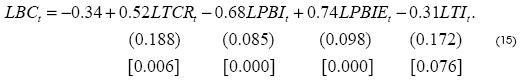
En los resultados estimados en la ecuación (15) se observa que los coeficientes de las variables guardan la relación esperada y además son estadísticamente significativos a un valor de 5% de significancia. Además, el parámetro que muestra el efecto del tipo de cambio real sobre la balanza comercial en el largo plazo es mayor a cero,

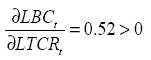
lo que demuestra, que para el período 2000-2018 se cumple la condición Marshall-Lerner en el largo plazo, dada por la ecuación (13), la misma que es aumentada por los términos de intercambio.

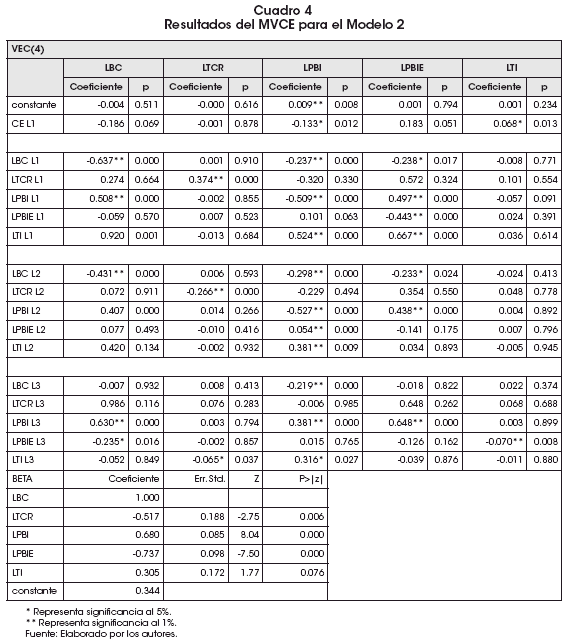
Para verificar la existencia del fenómeno de la Curva-J, tras el modelo de largo plazo estimado en las ecuaciones (14) y (15), es necesario que una depreciación del tipo de cambio genere un incremento inicial en el cociente de las exportaciones e importaciones (BC), seguido de una disminución en la balanza comercial (BC), y que posteriormente el valor en la balanza comercial regrese a su estado inicial. Para tal fin se simula un shock transitorio en las ecuaciones estimadas (14) y (15), que impacta sobre el tipo de cambio real, y mediante la función de impulso-respuesta se observa el comportamiento de la balanza comercial (BC).

En el Gráfico 2 se muestran los resultados de un shock transitorio sobre el tipo de cambio para ambos modelos y su efecto sobre la balanza comercial, donde se advierte que posterior a este shock de tipo de cambio, la balanza comercial se mueve de su estado de equilibrio, alejándose de su estado inicial, y no regresa, como era de esperarse, sino que mantiene una tendencia creciente, lo que confirma el no cumplimiento de la Curva-J para la balanza comercial (BC) de los modelos descritos.

 

5. Conclusiones

El presente trabajo busca probar la condición Marshall-Lerner y la Curva-J para la balanza comercial del Perú utilizando información estadística mensual del período 2000-2018. En particular, se investiga si la devaluación del tipo de cambio real mejora la balanza comercial, para lo cual se plantean dos modelos para testear la condición dada. Utilizando la metodología de cointegración de Johansen, se encuentra evidencia de la existencia de una ecuación de cointegración para los dos modelos planteados para la balanza comercial; luego, empleando la ecuación normalizada de Johansen, se verifica la validez de la condición Marshall-Lerner mediante la ecuación de largo plazo para la balanza comercial, encontrándose que para el caso peruano la depreciación tiene impacto positivo sobre la balanza comercial. Seguidamente, para verificar la posible existencia de una Curva-J en los modelos de largo plazo, se simula un shock que impacta sobre el tipo de cambio real mediante la función de impulso-respuesta, demostrando que no existe tal fenómeno, ya que, como respuesta al shock de tipo de cambio real, la balanza comercial no regresa a su estado inicial de equilibrio. Por otro lado, para futuros trabajos se sugiere probar la condición Marshall-Lerner con una metodología que considere la dinámica y los posibles quiebres estructurales en el período de estudio, para lo cual se recomienda proyectar y medir el error ocurrido para evaluar su eficiencia.

 

Agradecimientos

Los autores agradecen a Dios nuestro Señor por la guía y bendición. Asimismo, agradecen a los revisores anónimos que contribuyeron con sus aportaciones para mejorar el trabajo.

 

Notas

* Universidad Nacional del Altiplano, Perú (UNAP) y Grupo Fibonacci de Ciencias Económicas (GRFICE). Autor de correspondencia. Contacto: flaurenteblanco@gmail.com

** Universidad Nacional del Altiplano, Perú (UNAP). Contacto: machaca.dan@gmail.com

1 Para más detalle, se sugiere revisar los documentos de los autores de esta metodología: Johansen (1988) y Johansen y Juselius (1990).

 

Fecha de recepción: 8 de julio de 2019
Fecha de aceptación: 30 de septiembre de 2019
Manejado por ABCE/SEBOL/IISEC

Referencias

1. Abd-El-Kader, E. S. M. (2013). “Is the J-Curve Effect Observable for Egypt Economy?” Journal of Economic Cooperation and Development, 34(2)1, 91-118.

2. ADEX. (2019). Nuevo récord, nuevos retos de las exportaciones. Lima, Perú. Disponible en http://www.adexperu.org.pe/lista-boletines/        [ Links ]

3. Ali, A., Nafees, B. y Farid, N. (2017). “Marshall-Lerner Condition for South Asia: A Panel Study Analysis”. Pakistan Journal of Commerce and Social Sciences, 11(2), 559-575.

4. Ardila, P., Mora, L. y Cuevas, P. (2018). Análisis de la condición Marshall-Lerner en Colombia para el subsector alimentos y el azúcar. Universidad de La Salle, Bogotá.

5. Arriaga, R. y Landa, H. (2016). “Competitividad del sector externo mexicano: un análisis de la condición Marshall-Lerner”. Revista Mexicana de Economía y Finanzas, 11(1), 79-101. Disponible en: http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1665-53462016000100079&lng=en&tlng=en

6. Backus, D. K., Kehoe, P. J., Kydland, F. E., American, T., Review, E. y Mar, N. (2007). “Dynamics of the Trade Balance and the Terms of Trade: The J-Curve?” The American Economic Review, 84(1), 84-103.

7. BCRP. (2018). Sistemas de consultas estadísticas (varios años). Disponible en: https://estadisticas.bcrp.gob.pe/estadisticas/series/ Consulta: 6 de marzo de 2018.        [ Links ]

8. Beltrán, D. (2016). Cumplimiento de la condición de Marshall- Lerner en el comercio de Colombia con Chile, México y Perú para los sectores agricultura, minería y manufactura. Pontifica Universidad Javeriana.        [ Links ]

9. Bravo, R. (2009). Impacto del tipo de cambio en la balanza comercial de México: la condición de Marshall-Lerner y su efecto de la curva J, 1993-2008. Universidad Autónoma Agraria Antonio Narro, México.

10. Bustamante, R. y Morales, F. (2009). “Probando la condición de Marshall-Lerner y el efecto Curva-J: Evidencia empírica para el caso peruano”. Estudios Económicos, (16), 103-126.

11. Cambazoglu, B. y Gunes, S. (2016). “Marshall-Lerner condition analysis: Turkey case”. Economics, Management, and Financial Markets, 11(1), 272-283.

12. Caporale, G. M. y Gil-Alana, L. A. (2012). “Robert Mudida Testing the Marshall-Lerner Condition in Kenya”. German Institute for Economic Research, Discussion Paper 1247.

13. Chena, P. I. y Bosnic, C. (2017). “Concentración económica y comercio internacional. La condición Marshall-Lerner en la Argentina (1993-2013)”. Cuadernos de Economía, 36(71), 379-403. Disponible en: https://doi.org/10.15446/cuad.econ.v36n71.54921

14. Dickey, D. A. y Fuller, W. A. (1979). “Distribution of the Estimators for Autoregressive Time Series With a Unit Root”. Journal of the American Statistical Association, 74(366), 427-431. Disponible en: https://doi.org/10.2307/2286348

15. Eita, J. H. y Africa, S. (2013). “Estimation of the Marshall-Lerner condition for Namibia”. International Business & Economics Research Journal, 12(5), 511-518.

16. Granger, C. W. J. (1980). “Testing for causality. A personal viewpoint”. Journal of Economic Dynamics and Control, 2(C), 329-352. Disponible en: https://doi.org/10.1016/0165-1889(80)90069-X

17. ---------- (1988). “Some recent development in a concept of causality”. Journal of Econometrics, 39(1-2), 199-211. Disponible en: https://doi.org/10.1016/0304-4076(88)90045-0

18. Johansen, S. (1988). “Statistical analysis of cointegration vectors”. Journal of Economic Dynamics and Control, 12(2-3), 231-254. Disponible en: https://doi.org/10.1016/0165-1889(88)90041-3

19. Johansen, S. y Juselius, K. (1990). “Maximum Likelihood Estimation and Inference on Cointegration - With Applications To the Demand for Money”. Oxford Bulletin of Economics and Statistics, 52(2), 169-210. Disponible en: https://doi.org/10.1111/j.1468-0084.1990.mp52002003.x

20. Krzyzanowski, J. T. (2017). “The Standard Model of Trade and the Marshall–Lerner Condition”. Scientific Journal Warsaw University of Life Sciences, 17(4), 193-198. Disponible en: https://doi.org/10.22630/PRS.2017.17.4.95

21. Lal, A. K. y Lowinger, T. C. (2012). “The J-Curve: Evidence from East Asia”. Journal of Economic Integration, 17(2), 397-415. Disponible en: https://doi.org/10.11130/jei.2002.17.2.397

22. Lerner, A. (1944). The Economics of Control. New York: Macmillan.        [ Links ]

23. Mackinnon, J., Haug, A. y Michelis, L. (1999). “Numerical distribution functions of likelihood ratio tests for cointegration”. Journal of Applied Econometrics, 577(September 1996), 563-577. Disponible en: https://doi.org/https://doi.org/10.1002/(SICI)1099-1255(199909/10)14:5<563::AID-JAE530>3.0.CO;2-R

24. Onakoya, A. B. y Johnson, S. B. (2018). “Exchange Rate and Trade Balance: The Case for J-curve Effect in Nigeria”. KIU Journal of Social Sciences, 4(4), 47-63.

25. Pandey, R. (2013). “Trade Elasticities and the Marshal Lerner Condition for India”. Global Journal of Management and Business Studies, 3(4), 423-428.

26. Phillips, G. D. A. y Perron, P. (1988). “Testing for a Unit Root in Time Series Regression”. Biometrika, 75(2), 335-346. Disponible en: https://doi.org/10.2307/2336182

27. Sadok, H. (2018). “The Effect of Exchange Rates on Trade Balance : An Empirical Study of Morocco”. Journal of Business and Economics Review, 3(1), 1-10.

28. Sastre, L. (2005). “Simultaneidad exportaciones e importaciones, curva J y condición de Marshall-Lerner, en España”. Tribuna de Economía, (824), 209-222.

29. ---------- (2010). “Economías abiertas y condición de Marshall-Lerner”. Economic Analysis Working Papers Nº 09.

30. Schaling, E. y Kabundi, A. (2014). “The Exchange Rate, the Trade Balance and the J-Curve effect in South Africa”. SAJEMS, 17(5), 601-608.

31. Sek, S. K. y Har, W. M. (2014). “Testing for Marshall-Lerner Condition: Bilateral Trades between Malaysia and Trading Partners”. Journal of Advanced Management Science, 2(1), 23-28. Disponible en: https://doi.org/10.12720/joams.2.1.23-28

32. Siklar, I. y Celik, M. (2018). “Estimation of the Marshall-Lerner Condition and J Curve Dynamics for Turkey”. International Journal of Economics and Financial Research, 4(2004), 125-130.

33. Türkay, H. (2014). “The validity of Marshall-Lerner condition in Turkey: A cointegration approach”. Theoretical and Applied Economics, XXI(10), 21-32.

34. Velazco, J. y Pinilla, V. (2017). “Development Models, Agricultural Policies, and Agricultural Growth: Peru, 1950-2010”. Sociedad de Estudios de Historia Agraria (August), 1-27. Disponible en: https://doi.org/10.13140/RG.2.2.32972.10886