Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Latinoamericana de Desarrollo Económico
versión On-line ISSN 2074-4706
rlde no.31 La Paz mayo 2019
Cientific Article
A Regional Landscape of Bolivian Economic Growth
Un panorama regional del crecimiento económico boliviano
Pablo Mendieta Ossio*
Abstract
Bolivia is a wide surface country, with more than one million of squared kilometers and diverse ecological ecosystems. Besides its landlockedness, Bolivian economic activity has been shaped by the diverse geographic characteristics mainly distance and the availability of communication channels. In this paper I use a novel regional database of regional economic activity to analyze in what extent the spatial dimension has influenced medium term economic growth of the nine regions during the past 45 years. Contrary to standard approach based on contiguity or geographical distance to introduce spatial issues in the analysis, I use an exponential decay approach built on "true distance" jointly a gravity model. Then, I found as significant the inclusion of spatial consideration in the estimation of static and dynamic balanced panel data models, where I found how the process of regional economic growth has been slightly influenced by this spatial feature implying the still low degree of integration among Bolivian regions.
Key words: Regional economic growth, panel data; spatial econometrics.
Resumen
Bolivia es un país con una superficie amplia, con más de un millón de kilómetros cuadrados y diversos ecosistemas ecológicos. Además de su mediterraneidad, la actividad económica boliviana se ha marcado por las diversas características geográficas, principalmente la distancia y la disponibilidad de canales de información. En este documento uso una de base de datos regional para analizar en qué medida la dimensión espacial ha influido en el crecimiento económico a mediano plazo de los nueve departamentos durante los últimos 45 años. Contrariamente a la aproximación convencional, basada en la contigüidad o la distancia geográfica para introducir problemas espaciales en el análisis, uso un enfoque de decaimiento exponencial basado en la "distancia verdadera" conjuntamente con un modelo de gravedad. Luego, encuentro como significativa la inclusión del aspecto espacial en la estimación de modelos de panel estáticos y dinámicos, donde encuentro cómo el proceso de crecimiento económico regional se ha visto ligeramente influenciado por esta característica espacial, lo que implica el aún bajo grado de integración entre los departamentos de Bolivia.
Palabras clave: Crecimiento económico regional, datos de panel, econometría espacial.
Classification/Clasificación JEL CODES: C31, O54, R11.
1. Motivation
One of the best-known geographical features of Bolivia is its landlockedness. In fact, there is empirical evidence that landlocked countries grow at a lower rate than non-landlocked ones, even this perverse effect could be partially mitigated with good policies (Paudel, 2014), and greater emphasis to logistic and infrastructure (Arvis et al., 2010). But besides this renowned characteristic of Bolivian political geography, there another geographical factor which affects global and regional economic growth of the country and the nine regions compose Bolivia. This is the large and diverse surface, with more than one million of squared kilometers (the 28th largest in the world) and a difference of elevation from 6.542 meters above the level sea in the Sajama to 70 meters near the Paraguay river. Also, Bolivia comprises 13 ecological regions from the Andeans to the Amazon basin.
There is also another geographical factor is the remoteness to main markets, a feature which is common to most of Southern part of Latin America. A survey about this factor and its influence in trade patterns, including external trade composition, is found in Robertson and Robitaille(2017).
Then, I will address the question on how the second geographical characteristic has shaped the economic growth of the nine regions during the last five decades. Specifically, I will focus on the evidence of convergence including spatial consideration and the dynamics of regional economic growth and the relationship across the regions.
Domestic distance matters for the composition of exports. For example, Morales and Sachs (1989) pointed out that high transportation costs resulted in emphasis in high value added per unit weight exports, mainly mining resources. This resulted in a low degree of diversification. So, I will focus on how distance within Bolivian regions could explain actual regional composition of GDP and its dynamics since 1970.
To answer this question, I will use techniques of spatial econometrics, mainly promoted during the last years by Anselin and Rey (2014), with emphasis on panel data. This approach was developed by Elhorst (2013) as well as a spatial variant of the well-known method for the estimation of dynamic panels developed by Arellano and Bond (1991) and modified by Lee and Yu (2014). They provide a suitable way to incorporate distance issues in econometric estimation.
The paper is organized as follows. After this introduction, I describe the dataset used in this paper, where I emphasize the novel nature of it. Then I will define how I can include distance in the econometric estimation, given the diverse nature of Bolivian landscape, discussing if it affects the previous findings on regional convergence. After that, I will estimate a balanced panel data regression of the dynamics of regional Bolivian economic growth to try to answer how a shock could affect other regions. I conclude this paper with a discussion of the results.
2. A novel database of Bolivian Regional Economic Activity
Actually, official figures of regional economic activity are released by the National Institute of Statistics (INE), with the method of 'base year', fixed in 19901. Data is available since 1988 in its web site. However, it is possible to infer previous data because INE made previous efforts to quantify regional economic activity in the seventies and eighties. Published reports account that INE calculated regional GDP during the seventies with the base year 1970 and the period between 1980 to 1986 with base 1980. These database are only available on printed format in COPSCZ (1982) and INE-Bolivia (1992).
Fortunately, during the process of building the database Santa Cruz Data2, sponsored by the Chamber of Industry and Commerce of Santa Cruz (CAINCO), there was a retropolation of regional data. It is available at the mentioned web address for the period 1965 to 2015 for Santa Cruz. Although it has not been published, the retropolation of GDP also considered the other eight regions of Bolivia for the period 1970 to 2014. It must be noted that until the crafting of this work, it was the unique long run data available.
Given the nature of it, I use this database for the present research3. There is available regional GDP data for 45 years. The specific series were built using retropolation of total GDP, not sectoral one. Except for 1987, where it was constructed using the regional composition of Bolivian GDP found in Villarroel( 1992), the previous method was used to build a whole series real GDP valued at 1990 prices. To avoid the problem of non-stationarity, I use the logarithmic growth of the GDP regional series yit = Δln(GDPi,t) = ln(GDPi,j) - ln (GDPi,t-1), where i represents the region and t the year4.
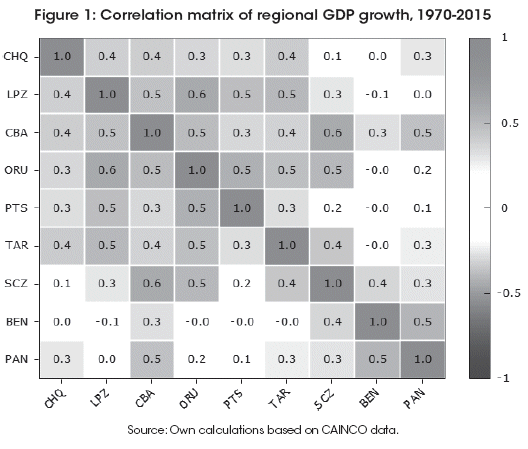
It allows us to see the relationship between regions. A first and basic analysis of the correlation matrix R, where the generic element ri,j . is the linear correlation between growth of region i with the correspondent of region j. It could be seen in form of heathmap (Figure 1) and it shows correlations across Bolivian regions.
The correlation across regions is statistically significant. The exceptions are i) Chuquisaca with Santa Cruz, Beni and Pando, ii) La Paz, Oruro, Tarija and Potosi with Beni and Pando, iii) Potosi with Santa Cruz.
3. The Diversity of Bolivian Geography and its Inclusion in Econometric Analysis
In the current section I will discuss the construction of the spatial weight matrix, a key element of the analysis of spatial relationships across Bolivia and why it must be built with a different approach than the conventional ones5.
In order to set the main ideas, suppose we have a time series for a typical region i of n ones that compose a country, all of them in form a balanced panel data. We will assume a very simplistic specification with some region specific and time specific dichotomic variables and a linear trend:
![]()
Where αi is a specific factor affecting region i, γt is a common factor during the period t. It must be noted that yi,t = Δln(GDPi,t). Simplifying the previous expression for a single equation estimation, we have the econometric specification:
![]()
If we like to estimate the effects of other regions on economic activity of region i, then a more suitable specification is:
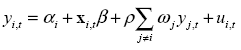
Where ωj is the weight attached to the effect of region j to region i and ρ is a global spatial correlation across regions. Obviously, for i = j the weight wj = 0. In matrix notation:
![]()
The matrix Y = [y1 y2...yi ...yn] is matrix containing whole regional time series of all the country.
But this description is incomplete because it does not include feedback effects. For example, a shock in region i will have spillovers in another regions j different than i. But them also have spillovers in the same regioni. So, a better description of the system is better to use the matrix W = [w1 w2...wi ...wn]' . Then:
![]()
Then, to find the final equilibrium of the system, it is easy to prove than the previous system could be stated as:
![]()
Therefore, it will be crucial how we create the weight matrix.
Anselin and Rey (2014) propose two methods. The first one is based on contiguity across regions while the second rests on distance, mainly from the centroids of every region. Both are misleading if they are applied to Bolivia without any adjustment, while they have been applied to many contiguous regions assuming that they have good communication ways, besides the general critique to these ways found in Fiaschi and Parenti (2014).
Given that we are considering just the nine main regions with different ecological zones and elevations and there are no communication ways in many cases, I will apply a modified version of the distance exponential decay, generally defined as:
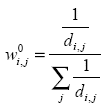
Where di,j is the distance of the main way between capitals of regions i and j. I have constructed this matrix of inverses of distances and times of travel according Google Maps information of travel time at June of 2018. This goes along the spatial specification suggested in Chen (2012), known also as the Cliff-Ord weights.
Nevertheless, this approach would be inadequate if we do not consider differences of population of different capital cities. So, following the approach of Day and Lewis (2013), I will add an additional term related to the 'gravity' view, where the weight, broadly speaking, is:
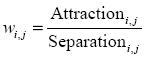
Then, I will use the following weight:
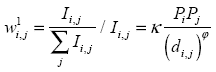
In this case, I use a 'gravity approach' suggested by Chen (2015), where Pi is the population of the capital city of region i. I am using the geometric mean between population measured in 1976 census and 2012 census.
In the case of the parameter φ, it lies between 0 and 3. I calibrated this parameter according with the value that maximizes the correlation between W1 and the matrix of correlations R which deliver a value of at 1.69. Besides, I calibrate the parameter κ in order that max(Ii,j) = 1.
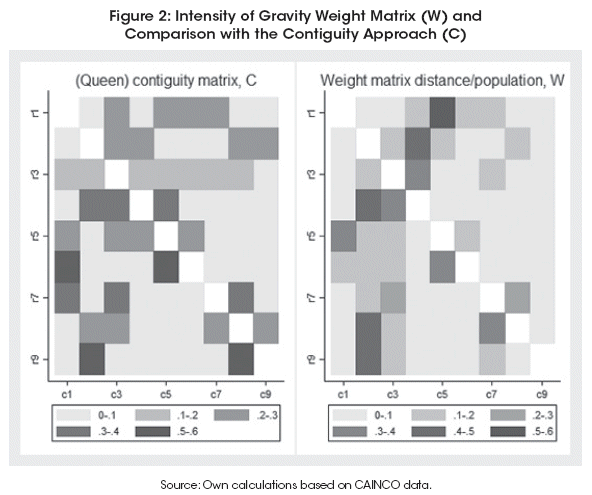
The matrix according this concept is shown in Figure 2, where it is compared to the contiguity weight matrix. The weighting approach followed with the distance/population scheme creates a more diverse spatial pattern than the one that is based on contiguity.
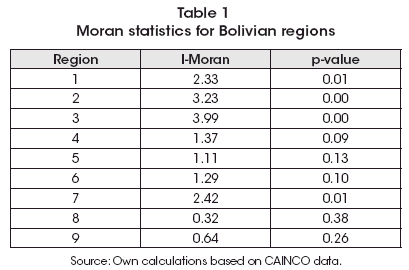
With the previous weight matrix, I computed the I-Moran statistic for complete series, shown in Table 1, where spatial correlation is important for less than half of Bolivian regions: Chuquisaca, La Paz, Cochabamba and Santa Cruz, while there is some weak evidence in the rest of cases.
Given the detail about the weight matrix, I will estimate in the following section a panel with determinants of regional economic growth including some interdependence between the data.
4. Medium run Fundamentals of Regional Economic Growth in Bolivia
There are two issues I will address in this section. The first is which were the determinants of the regional economic growth in Bolivia, while the second is if there is a spatial pattern behind this relationship.
To focus these issues, I will use a spatial panel methodology, estimating some selected models. Using previous estimates, I will regress regional GDP growth respect to three variables I found significant in previous studies, mainly in Mendieta and Martin (2009). They are the (log of) terms of trade, external growth relevant for Bolivia and a macroeconomic stability index. The last two were built according these formulas:
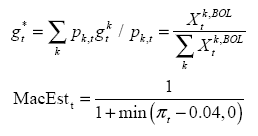
The first expression is a weighted average of main trade partners of Bolivia, where the weight is the share of exports of Bolivia to country k on total exports. In the case of macroeconomic stability, it is measured as the reciprocal of inflation, mainly to capture the hyperinflation period between 1982 to 1985.
I must add that these series and the regional growth ones are all stationary. In the case of regional series, I ran the Im-Shin test of panel unit root test. In other cases, the standard Augmented Dickey Fuller, so I can apply a diversity of models for panel data without unit root considerations.
To estimate these panels, I use the routine created by Belotti et al. (2017) while the standard tools of usual panel data are applied to non-spatial models. I will estimate some kinds of models given the impressive advance in this econometric area, as it is reviewed in Elhorst (2013). After choosing the most relevant, then I will discuss the direction and magnitude of estimated effects.
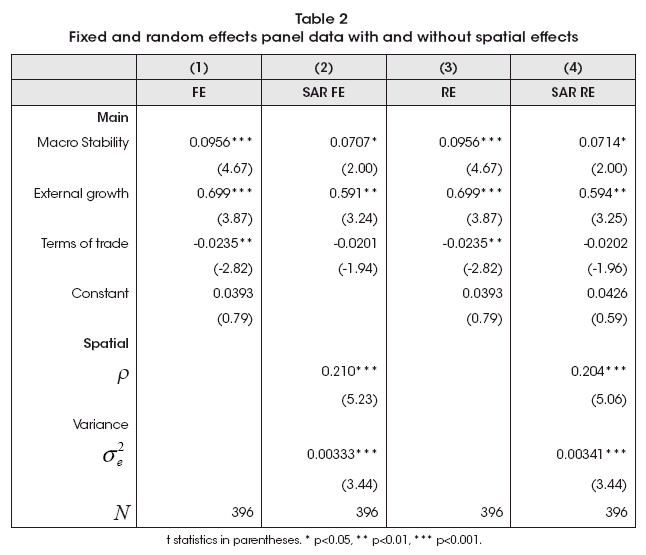
The first models are the classical Fixed Effects (FE) and Random Effects (RE) which I estimated with and without spatial lag error (Spatial Auto-Regressive or SAR) of the form Y = Xβ +ρWY + u, a denomination popularized since Anselin (1988). Results are shown in Table 2.
These estimates are consistent with the importance of macroeconomic stability and a strong effect of foreign conditions, mainly of economic activity. In the case of terms of trade, it is not significant when we include some spatial consideration. It is important to note that spatial consideration seems relevant according two models estimated with a parameter of spatial correlation (ρ) around 0.2.
Finally, the Hausman test, explained with detail in Wooldridge (2010), delivers a value of χ2(4) = 6.79, which is consistent with no systematic differences between FE and RE estimates.
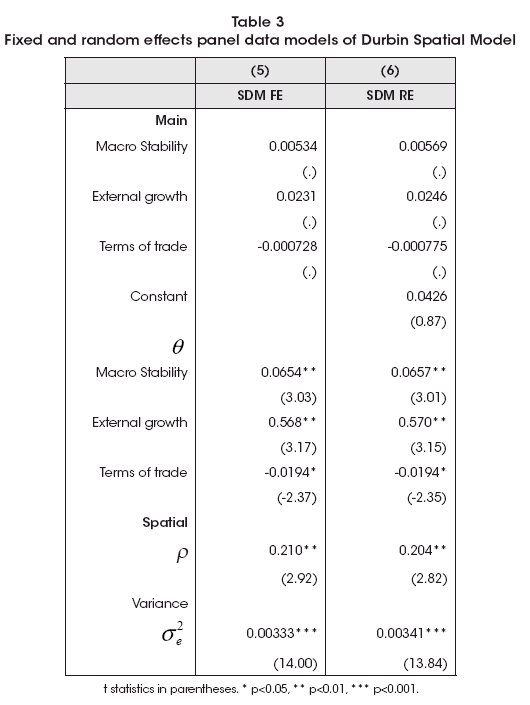
The second class of models are the classical Fixed Effects (FE) and Random Effects (RE) for the Spatial Durbin Model (SDM) of the form Y = Xβ + ρWY + WXθ + u. Results are shown in Table 3. It could be seen that spatial parameter is like the SAR model, around 0.2, as in previous regressions.
Regarding the parameters, it must be noted that β are close to zero while θ was close to βSAR . I have broadly crossed this information with Instrumental Variable estimation method of Alvarez et al. (2017). Then, I will focus in the SAR model (models 2 and 4).
Macroeconomic stability parameter is like the SAR model, while there is smaller effect of external growth. However, terms of trade become significant in this alternative approach. So external determinants of Bolivian whole and regional growth remain significant. Due absence of asymptotic properties, a Hausman test was not feasible to perform, as was cautioned by Belotti et al. (2017).
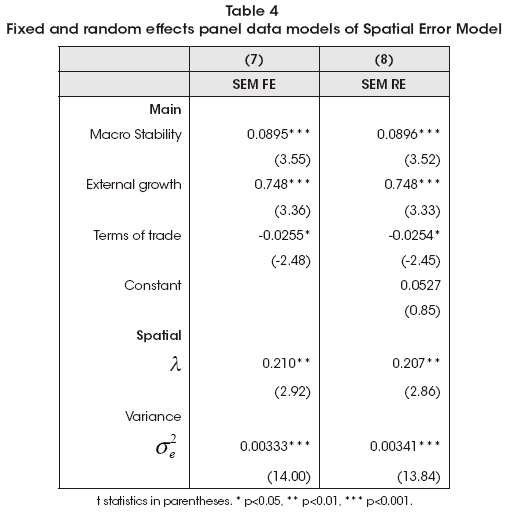
The third class of models to be estimated are the Spatial Error Model (SEM), which takes the form of Y = Xβ + u where u = λWu + ν . Results are shown in Table 4. In this case, spatial spillovers come from the disturbances or innovations, where the main model is free of spatial interactions.
As the previous case, the results are coherent with other ways to estimate this spatial pattern as the effects of the determinants of regional economic growth. So, we have at least two approaches that could be relevant to study the effects: the SAR one and the SEM.
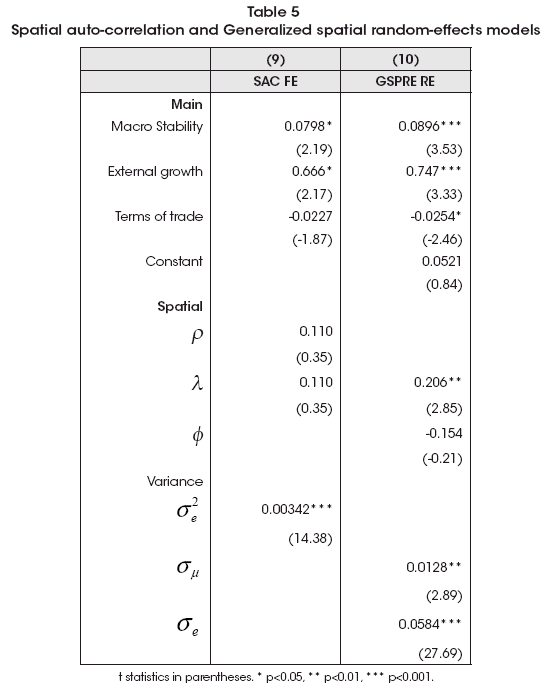
In order to be exhaustive in the econometric procedure and choose which seems more suitable for the analysis, I will estimate two kinds of models. The first one are other two extensions of spatial models as the Spatial Autoregressive with Fixed Effects (Y = Xβ+ ρWY + WXθ +u/u = λWu + ν) and the Generalized spatial random-effects model (Yt = Xβ+ u + Zt /u = λWu + ν![]() Zt = ΦWzt + wt). The estimates of these models are shown in Table 5, where these more general specifications point to a SEM one, which seems more parsimonious than both.
Zt = ΦWzt + wt). The estimates of these models are shown in Table 5, where these more general specifications point to a SEM one, which seems more parsimonious than both.
The last kind of models to be tested are those with both spatial and temporal lags. The general specification is Yt = ![]() Yt-1 + Xtβ + ρWYt + ut . Let us denote Lt as the temporal lag operator (Ltxt = Xt-1) and Ls the spatial lag operator (LSxt = Wxt). Then, the previous specification becomes as:
Yt-1 + Xtβ + ρWYt + ut . Let us denote Lt as the temporal lag operator (Ltxt = Xt-1) and Ls the spatial lag operator (LSxt = Wxt). Then, the previous specification becomes as:
![]()
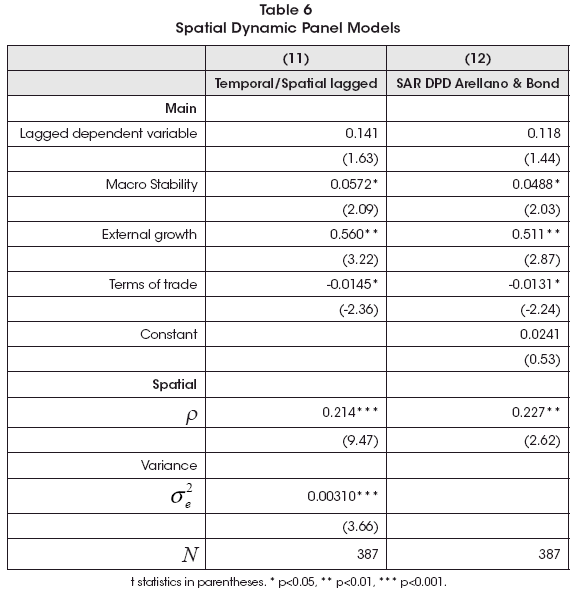
To estimate these models, I have used two variants. The first one is the used in previous regressions while the second is the spatial variant of the well-known Dynamic Panel Data (DPD) model of Arellano and Bond (1991), with the spatial specification of Shehata and Mickaiel (2012). They correct bias estimates due the correlation that arises between regression variables and the error term given the demeaning process involved in this process. Both estimations are in Table 6.
Both approaches deliver similar results: there is a weak signs of dynamic temporal lag significance. So, a spatial static model seems more reliable to analyze than the dynamic one. This is consistent with the low degree of temporal autocorrelation found in the analysis of the data as the non-significance of the parameter related to the lagged dependent variable in non-spatial DPD models (not reported).
So, we have a wide range of models. To choose which could be more relevant I will use the Bayesian Information Criteria (BIC). Given this approach, I will use these models as equivalent ones:
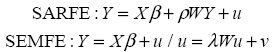
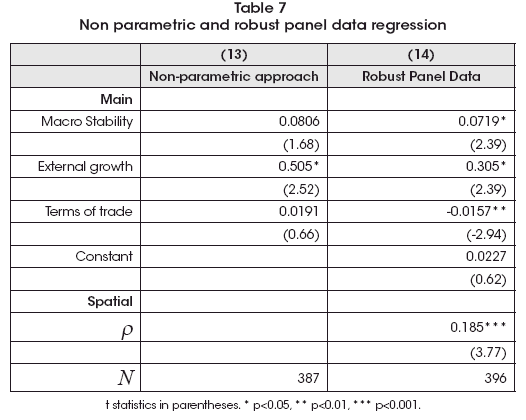
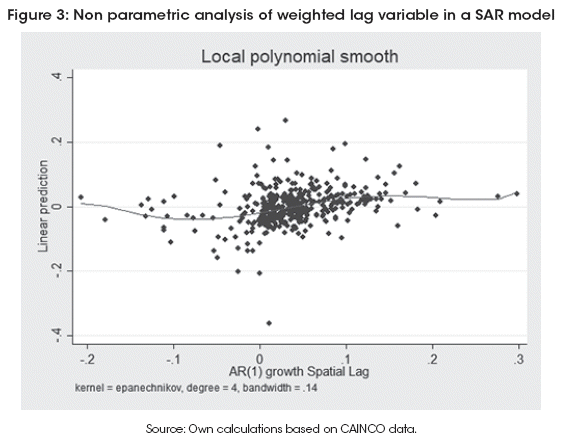
In order to finish the estimation stage, I will add two other robustness analysis. The first is to find if there is non-linearity in the weighted spatial lag (ρW), through a non-parametric approach. Results of the estimation is on the left side of Table 7, while Figure 3 shows the non-parametric estimate of the parameter ρ, following the procedure created by Verardi and Libois (2012) according the method proposed by Baltagi and Li (2002). It could be seen that there is a near linearity effect of spatially lagged variable.
So, I will use the following relationships:
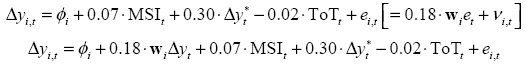
Where MSI is the Macroeconomic Stability Index, ToT is Terms of Trade and Δy*t is the external growth relevant for Bolivia.
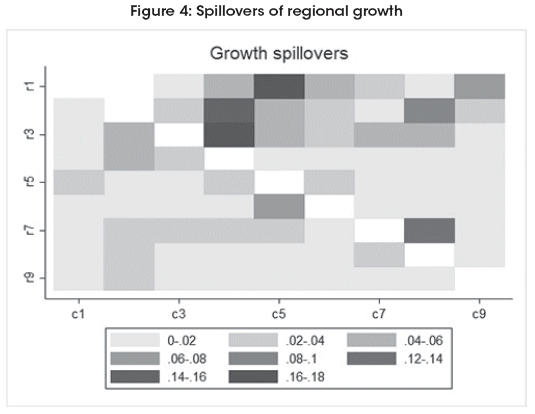
Given that I am interested to analyze the spatial pattern and spillovers, I will simulate the effects of one standard deviation of region i growth in the other regions, coherent with the weight matrix and the estimated spatial parameter. This is, I will compute the matrix Φ = (I-ρW)-1 z, where the vector is normalized against its own standard deviation. This simulation is shown in Figure 4.
Even it could be expected that bigger regions could have more spillovers than small ones, this pattern is not found. In fact, there seems to be more relationships across similar regions.
There are some interesting features according the analysis:
Chuquisaca and Tarija are the most benefited by higher growth in Potosi, where the relationship goes from the last to the first ones.
Oruros shock favors La Paz and Cochabamba.
More activity in Beni is favorable for Santa Cruz.
Surprisingly, Beni and Pando are more benefited by La Paz than other regions.
So, there seems that the spatial pattern is clearer in the West part of Bolivia, which regions are part of cluster. The low relationship between the East and West side of Bolivia could be driven by still inadequate ways of communication. It is still visible in the magnitude of the spatial parameter.
5. Final remarks
In this document I tried to discover the spatial pattern behind the Bolivian economic growth since the seventies, with a novel database. I used extensively different econometric methods suitable for panel data, trying to look the more adequate for the analysis. I found that there are some spillovers across Bolivian regions, but they are probably clustered according the geographical regions they belong.
This result is coherent with the previously found in Montero and Del-Río (2013), where they do not find a clear spatial pattern when they analyze converge among Bolivian regions. The main implication is that different regions of Bolivia would not be communicated among them. It could be result of lack of infrastructure and logistics, which can deliver production from one region to another in a suitable and continued way.
Finally, this work could be improved with methodology considering time travel among different regions, which has changed in the time; or it could be enhances with an estimation of a heterogeneous spatial effect, like the recent analysis of LeSage and Chih (2017). This final robustness check could deliver more insights respect to the hypothesis of the lack of infrastructure and logistic in the Bolivian case.
Notas
* Head of the Bolivian Center of Economics at the Chamber of Industry and Commerce of Santa Cruz (CAINCO) and student of the PhD program in Economics at the Private University of Bolivia (UPB).The author is thankful for the comments of anonymous referee and the training received from Darwin Ugarte, Diego Escobari and Oscar Molina. Obviously, the responsibility is completely mine. The views expressed do not necessarily represent corresponding ones of any institution related to the author. Contacto: pablo.mendieta@cainco.org.bo
1 Currently, INE is carrying the change of base year and the methodology to 'chained' national accounts as many other countries.
2 Available at www.santacruzdata.com.
3 I am indebted with CAINCO, who supported this retropolation, for allowed me to use this data.
4 Some statistics and the complete series are available in the working paper version of this paper at https://sites.google.com/site/pmendiet/papers.
5 A good basic review of spatial models is found in Elhorst (2003).
Fecha de recepción: 28 de enero de 2019
Fecha de aceptación: 29 de marzo de 2019
Manejado por ABCE/IISEC
References
1. Álvarez, Inmaculada; Barbero, Javier and Zoo, José. (2017). “A panel data toolbox for Matlab”. Journal of Statistical Software, 76(6), 1-27.
2. Anselin, Luc. (1988). Spatial Econometrics: Methods and Models. Kluwer Academic Publisher. [ Links ]
3. Anselin, Luc and Rey, Sergio Joseph (2014). Modern Spatial Econometrics in Practice: A Guide to GeoDa, GeoDaSpace and PySAL. Chicago: GeoDa Press.
4. Arellano, Manuel and Bond, Stephen. (1991). “Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations”. The Review of Economic Studies, 58(2), 277-297.
5. Arvis, J.F.; Raballand, G. and Marteau, J.F. (2010) The Cost of Being Landlocked: Logistics Costs and Supply Chain Reliability. Directions in Development. World Bank Publications.
6. Baltagi, Badi and Li, Dong. (2002). “Series estimation of partially linear panel data models with fixed effects”. Annals of Economics and Finance, 3(1):103-116.
7. Belotti, Federico; Hughes, Gordon and Piano Mortari, Andrea. (2017). “Spatial panel data models using Stata”. Stata Journal, 17(1), 139-180.
8. Chen, Yanguang. (2012). “On the four types of weight functions for spatial contiguity matrix”. Letters in Spatial and Resource Sciences, 5(2), 65-72.
9. ---------- (2015). “The distance-decay function of geographical gravity model: Power law or exponential law?”. Chaos, Solitons & Fractals, (77), 174-189.
10. COPSCZ. (1982). Diagnóstico agropecuario del departamento de Santa Cruz. Comité de Obras Públicas de Santa Cruz. [ Links ]
11. Day, Jennifer and Lewis, Blane. (2013). “Beyond univariate measurement of spatial autocorrelation: disaggregated spillover effects for Indonesia”. Annals of GIS, 19(3), 169-185.
12. Elhorst, J. Paul. (2003). Specification and estimation of spatial panel data models. International Regional Science Review, 26(3), 244-268. [ Links ]
13. ---------- (2013). Spatial Econometrics: From Cross-Sectional Data to Spatial Panels. Springer Briefs in Regional Science. Springer Berlin Heidelberg. [ Links ]
14. Shehata, Emad-Abd Elmessih and Mickaiel, Khaleel Sahra (2012). "Spregdpd: Stata module to estimate spatial panel Arellano-Bond linear dynamic regression: Lag & Durbin models". Statistical Software Components, Boston College Department of Economics.
15. Fiaschi, Davide and Parenti, Angela. (2014). “How Reliable are the Geographical Spatial Weights Matrices?” Region et Developpement, (40), 53-68.
16. INE-Bolivia. (1992). “Cuentas regionales de Bolivia por actividad economica (serie 1980-1986)”. Instituto Nacional de Estadistica, Division de Cuentas Regionales.
17. Lee, Lung-fei and Yu, Jihai. (2014). “Efficient GMM estimation of spatial dynamic panel data models with fixed effects”. Journal of Econometrics, 180(2), 174-197.
18. LeSage, James and Chih, Yao-Yu. (2017). “A matrix exponential spatial panel model with heterogeneous coefficients”. Geographical Analysis, 50 (4), 422-453.
19. Mendieta, Pablo and Martin, Dennise. (2009). “En busca de los determinantes del crecimiento económico boliviano”. Document presented at the 2009 Bolivian Conference on Development Economics.
20. Montero, Casto and Del-Río, Marco. (2013). Convergencia en Bolivia: un enfoque espacial con datos de panel dinámicos”. Revista de Economía del Rosario, 16 (2), 233.
21. Morales, Juan Antonio and Sachs, Jeffrey D. (1989). “Bolivia’s Economic Crisis”, book 3, 57-80. University of Chicago Press.
22. Paudel, Ramesh C. (2014). “Economic growth in developing countries: Is landlockedness destiny?”. Economic Papers: A journal of applied economics and policy, 33(4), 339-361.
23. Robertson, Peter E. and Robitaille, Marie-Claire. (2017). “The tyranny of distance and the gravity of resources”. Economic Record, 93(303), 533-549.
24. Verardi, Vincenzo and Croux, Christophe. (2009). “Robust regression in stata”. Stata Journal, 9(3), 439-453.
25. Verardi, Vincenzo and Libois, Francois. (2012). “XTSEMIPAR: Stata module to compute Semiparametric Fixed-Effects Estimator of Baltagi and Li”. Statistical Software Components, Boston College Department of Economics, February, 2012.
26. Villarroel, David. (1992). “Descentralización y políticas de población (Bolivia)”. Technical report, CEPAL. Disponible en: http://repositorio.cepal.org/handle/11362/21203.
27. Wooldridge, J.M. (2010). Econometric Analysis of Cross Section and Panel Data. MIT Press [ Links ]