Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Latinoamericana de Desarrollo Económico
versión On-line ISSN 2074-4706
rlde no.23 La Paz mayo 2015
ARTÍCULO CIENTÍFICO
Aplicación del algoritmo de Vartia: el sector de educación primaria en Bolivia
Vartia algorithm application: The primary education sector in Bolivia
Raúl Rubin de Celis Cedro*, Lourdes Espinoza Vásquez**
Resumen
La evaluación de cambios en el bienestar, desde un enfoque microeconómico, se ha concentrado en el cálculo de la variación equivalente y compensatoria a través del enfoque de integrabilidad. Sin embargo, el uso de esta metodología implica especificar de manera precisa la función de demanda de un bien o servicio. Dentro de las áreas sociales, la aproximación de funciones de demanda presenta varios inconvenientes, por lo que se pretende testear la robustez del algoritmo de Vartia y verificar si, en sectores como el de la educación, esta metodología puede constituirse en un mecanismo alternativo para la medición del bienestar cuando existen cambios en los niveles de precio.
Palabras clave: Bienestar, variación equivalente, variación compensatoria, Algoritmo de Vartia, integrabilidad.
Abstract
The standard approach in order to assess the changes in welfare is the calculation of the equivalent variation or the compensating variation, which relies in what the literature has been called the integrability method. This methodology needs a precise and well defined demand function. In general the use of empirical approximations for this demand function has many drawbacks. In this paper we test the robustness ofVartia algorithm instead of applying the integrability method. We verify that, in sectors like education, this algorithm can be used as an alternative mechanism to assess the changes in the welfare when the level of prices changes.
Keywords: Welfare, equivalent variation, compensating variation, Integrability Alghoritm of Vartia.
Clasificación/Classification JEL: D63; I31
1. El bienestar desde un enfoque microeconómico
El bienestar de un individuo representativo o de una sociedad es un concepto multidimensional muy difícil de aproximar en la evidencia empírica; más complicado aun es realizar una cuantificación del mismo. En esa línea, la teoría económica realiza aportes señalando, por una parte, que el bienestar puede ser visto a través de la suma del excedente del consumidor, y por otra, que los cambios en el bienestar, bajo un equilibrio parcial, se pueden aproximar mediante un análisis de indiferencia, calculando las variaciones equivalente y compensatoria1.
Cuando consideramos el excedente del consumidor y nos enfocamos en los cambios en el bienestar de un hogar o de un individuo, es relevante considerar las variaciones en los niveles de precio. Si estamos frente a una disminución de precios, el cambio en el excedente del consumidor es positivo, es decir, es una mejora en el bienestar del consumidor. En cambio, si estamos frente a una subida de precios, la variación del excedente del consumidor es negativa, es decir, implica una disminución en el bienestar del consumidor. El cálculo de esta área a través de una integral sería:
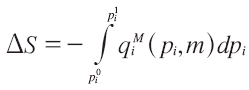
donde: qiM( pi,m) = demanda marshalliana de un bien
Por su parte, el empleo de las variaciones equivalente y compensatoria se basa en un análisis de indiferencia, en el que se considera que el bienestar viene reflejado por el cambio en los niveles de utilidad de un individuo cuando existen variaciones en los niveles de precio.
Recordemos que la Variación compensatoria (VC) se refiere a la cantidad de dinero (renta) que hay dar o quitar al individuo para dejarlo en su utilidad inicial con los precios finales; el consumidor puede por tanto recomponer su canasta de consumo después del cambio en precios. Por su parte, la Variación equivalente (VE) es la cantidad de dinero (renta) que hay que dar o quitar al individuo para dejarlo en el nivel de utilidad final con precios iniciales, es decir, como si los precios hubiesen cambiado, o situación equivalente a un cambio de precios (ver Cuadro 1).

Los conceptos de VC y VE guardan una estrecha relación con el enfoque de compensación de Hicks, según el cual, a partir de la búsqueda del efecto-sustitución y del efecto-ingreso, las medidas que estamos considerando definen la cantidad de dinero que hay que sustraer o dar al individuo después del cambio en precios o precios e ingreso real. Sin embargo, el problema con este enfoque es que la utilidad (U) es un concepto no observable y, por consiguiente, no cuantificable. Esto imposibilitaría contar con una medida del cambio en el bienestar del consumidor en términos cuantitativos; sin embargo, a través de las extensiones del problema primal y dual del consumidor podemos encontrar funciones como la Función de Utilidad Indirecta (V), que posee dentro de sus argumentos variables cuantificables como el precio (p) y el ingreso (m), que permiten medir o evaluar los cambios en los niveles de bienestar de un agente representativo.
Empleando las extensiones del problema primal y dual del consumidor, y con la ayuda de una función de utilidad indirecta se puede definir implícitamente la VC y la VE de la siguiente manera:
Si obtenemos los parámetros de la función de utilidad indirecta, podemos usar esta función (reemplazando precios e ingreso iniciales y finales) para obtener directamente la VC o la VE. Por otra parte, empleando la función de mínimo gasto podemos definir de manera explícita la VC y la VE para un cambio en el precio de la siguiente manera:
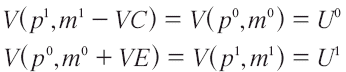
Si obtenemos los parámetros de la función de utilidad indirecta, podemos usar esta función (reemplazando precios e ingreso iniciales y finales) para obtener directamente la VC o la VE. Por otra parte, empleando la función de mínimo gasto podemos definir de manera explícita la VC y la VE para un cambio en el precio de la siguiente manera:
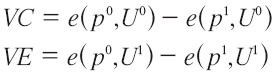
A partir de la definición explícita podemos obtener en términos de integrales la VC y la VE para un cambio en el precio. Para la VC tendríamos:
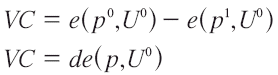
Si el cambio en el mínimo gasto con respecto al precio es:
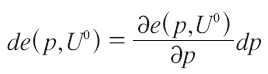
y por el lema de Shephard la derivada del gasto con respecto al precio es la demanda hicksiana, reemplazando, tenemos una expresión para la VC:
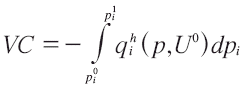
Para la VE, sería:
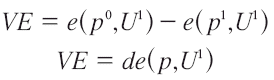
Si el cambio en el mínimo gasto con respecto al precio es:
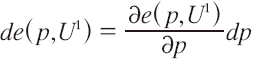
y aplicamos nuevamente el lema de Shephard, tenemos una expresión para la VE:
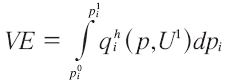
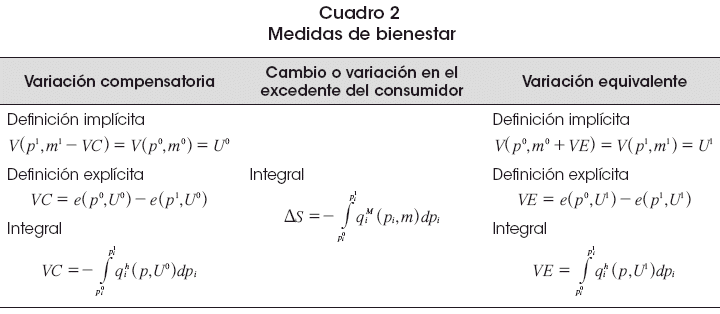
En el Cuadro 2 se puede observar un resumen de lo anterior:
2. Medición a partir de la dualidad: el problema de la integrabilidad
El problema de la integrabilidad consiste en recuperar la función de utilidad del consumidor a partir de la función de demanda; las implicaciones de lo anterior son significativas en cuanto al buen comportamiento de una función de demanda.
Recordemos que si x (p, m) es un sistema de funciones de demanda que maximizan la utilidad, se puede resumir el comportamiento observable del consumidor en los siguientes tres puntos (Jehle y Reny, 2011):
- Presupuesto equilibrado es decir: p · x (p,m) = m.
- Semidefinida negativa: la matriz de Slutsky asociada s (p,m) debe ser semidefinida negativamente.
- Simetría: s (p,m) debe ser simétrica
Estas tres condiciones garantizan que la función de demanda sea homogénea de grado cero en precios e ingreso, es decir que si los precios y el ingreso suben en una misma cuantía, la cantidad demandada debería seguir siendo la misma2.
De acuerdo con la intuición de Antonelli, si una función que depende de precios e ingreso satisface las tres condiciones anteriores, refleja la función de demanda para algún consumidor que maximiza su utilidad, es decir, es una función de demanda continuamente diferenciable de buen comportamiento y que agota la renta. Por su parte, de acuerdo a Border (2003), se puede considerar una función de demanda x* tal que:
![]()
la que se obtiene de un proceso de maximización de la utilidad u, y que al ser reemplazada en la utilidad inicial nos permite obtener una función de utilidad indirecta (V), que puede ser definida como:
![]()
Dado que u es no saciable localmente, la función de utilidad indirecta es estrictamente creciente en m.
Por su parte, la función de gasto hicksiana (℮) está definida por:
![]()
Del lema de Shephard se sabe que:
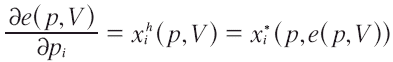
Suponiendo que V está dada, podemos tener la ecuación diferencial total:
![]()
La solución a la anterior ecuación diferencial y el valor de V se da considerando lo siguiente: Border (2003) señala que en el cálculo, por lo general, las ecuaciones diferenciales tienen muchas soluciones, a menudo indexadas por "constantes de integración". Por ejemplo, tomemos la ecuación diferencial simple:
![]()
Para alguna constante a, la forma general de la solución es:
![]()
donde C es una constante arbitraria de integración, lo que significa que la ecuación diferencial y' = a tiene infinitas soluciones, una para cada valor de C. Si asumimos el parámetro V como constante, entonces puede ser tomado como una constante de integración.
También se puede mencionar y rara vez especificar a C como una "condición" del problema, siempre y cuando no conozcamos la función "y" de antemano. En lugar de ello, usualmente se usa la condición inicial (x0, y0), especificando de la siguiente manera:
![]()
En este caso simple, la forma de trasladar la condición inicial en la constante de integración es resolver la ecuación:
![]()
y reescribir la solución como:
![]()
En vez de hacer explícito que la solución depende de las condiciones iniciales, muchos textos de ecuaciones diferenciales reescriben la solución como:
![]()
A partir de esto, se tratará de responder qué significaría resolver la ecuación diferencial de la sección anterior e'(p) = x*(p,e(p)), una condición inicial correspondiente para la "constante de integración" V es el par (p0,m0) que satisface:
![]()
De la equivalencia de minimización del gasto y maximización de la utilidad, sujetos a un presupuesto dado, obtenemos la relación:
![]()
De acuerdo a Hurwicz y Uzawa, definimos las funciones de ingreso compensadas en términos de la función de gasto hicksiana a través de e:
![]()
Obsérvese que:
![]()
y
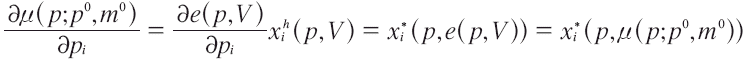
En otras palabras, las funciones de ingreso compensadas dan la solución a e(p) = μ(p;p0,m0), a la ecuación diferencial e'(p) = x*(p,e(p)); en términos de la condición inicial se tiene: e(p0) = m0.
Analizando la función de ingreso compensadas y (p0,m0) como variables de interés si fijamos cualquier precio, p* ∈ Rn++ y se define la función v: Rn++× R++:
![]()
La función "v" es otra función de utilidad indirecta. Esto es:
![]()
Para observar esto, e es estrictamente creciente en V,
![]()
Podemos usar v para encontrar la utilidad U, al menos en el rango de x* por:
![]()
Border (2003) detalla cómo se puede obtener la función de utilidad a partir de demandas de mercado. Dada una función de demanda x*:
a) resolver de "alguna forma"3 la ecuación diferencial:
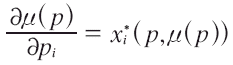
Escribir la solución de manera explícita en términos de las condiciones iniciales μ(p0) = m0 como μ(p;p0,m0).
b) Usar la función μ para definir la función de utilidad indirecta v:
![]()
c) Invertir la función de demanda para tener (p, m) como función de x*.
d) Definir la utilidad en el rango de x*:
![]()
3. Algoritmo de Vartia
El aporte del algoritmo de Vartia en materia de evaluación del bienestar es que se puede calcular el ingreso compensado, a partir de una aproximación numérica (Vartia, 1983). La ventaja de este algoritmo, a diferencia del problema de integrabilidad, es el cálculo de VC y VE sin la necesidad de recuperar funciones de utilidad y resolver ecuaciones diferenciales. El algoritmo se basa en una resolución a partir de técnicas iteradas numéricas de funciones de demanda implícitas, lo cual hace versátil el cálculo para cualquier función de demanda. En contrapartida, es necesario iterar la mayor cantidad de veces la aproximación numérica para poder tener un resultado lo más exacto posible; si el número de iteraciones tiende al infinito, el resultado siempre sería exacto. Claro está que también dependerá de la función de demanda para que la convergencia al resultado sea lo más rápido posible y no sea siempre en el infinito. Esta demás decir que, al ser una solución que se mejora conforme se realizan las iteraciones, ésta debe ser programada, puesto que a partir de cálculos manuales sería casi imposible tener resultados fehacientes.
Para analizar los cambios en el ingreso, Vartia parte de las condiciones de movimiento sobre las superficies de indiferencia. En lo que sigue se presenta una revisión del concepto básico sobre el cual fue construido dicho algoritmo, y la forma en la que éste se aproxima a los resultados obtenidos mediante la integrabilidad.
Sea t una variable auxiliar tal que 0≤ t ≤ 1 y que p(t); una curva diferenciable en el espacio de precios que conecta de p0=p(0) a p1=p(1). m(t) es cualquier nivel de ingreso desde m0=m(0). Si u(x) es una posible función de utilidad, entonces V(p, m)=u(x(p, m)) es la correspondiente función de utilidad indirecta. Diferenciando totalmente V(t)=V(p(t), m(t)) con respecto a t se tiene:
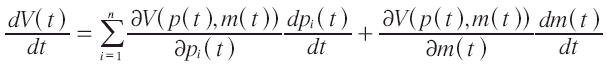
Lo anterior es la tasa de cambio en la utilidad para cada punto t cuando los precios p(t) e ingreso m(t) cambian de manera arbitraria. Usando la identidad de Roy tenemos:
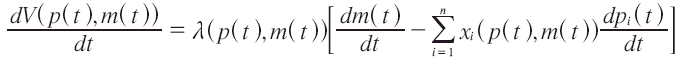
V(p,m) es estrictamente creciente en m, λ(p, m)>0, entonces la condición necesaria y suficiente para x(p(t), m(t)) de movimiento sobre la misma superficie de indiferencia es la tasa de cambio en la utilidad para cada t ∈ [0,1], lo que lleva a la ecuación diferencial de primer orden en m (t):
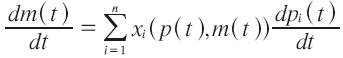
Ésta es la ecuación básica para el análisis de Vartia. Sin embargo, m(t) es una función desconocida a ser resuelta4. Para resolver la ecuación básica de Vartia, el autor aproximó el algoritmo a partir de métodos numéricos, cuya principal característica es la iteración para lograr una convergencia al resultado. Las técnicas más relevantes son: Método de Euler, Método de Euler mejorado o Formula de Heun, Método de Taylor de tres términos, Método de Runge-Kutta, Método de Adams-Bashforth/Adams-Moulton y Método de Milne. Para entender de donde sale la ecuación básica de Vartia se muestra la resolución del problema de pérdida o ganancia de bienestar del consumidor, mediante los primeros dos métodos señalados.
a) Método de Euler
Zill (1997) señala que una de las técnicas más simples para aproximar soluciones de ecuaciones diferenciales se conoce como método de Euler, o de las rectas tangentes. Supóngase que se desea aproximar la solución del problema de valor inicial:
![]()
Si h es un incremento positivo en el eje x, entonces se puede encontrar un punto (x1, y1)=(x0+h,y1) sobre la recta tangente a la curva de solución desconocida en (x0,y0), tal como se muestra en el Gráfico 1.
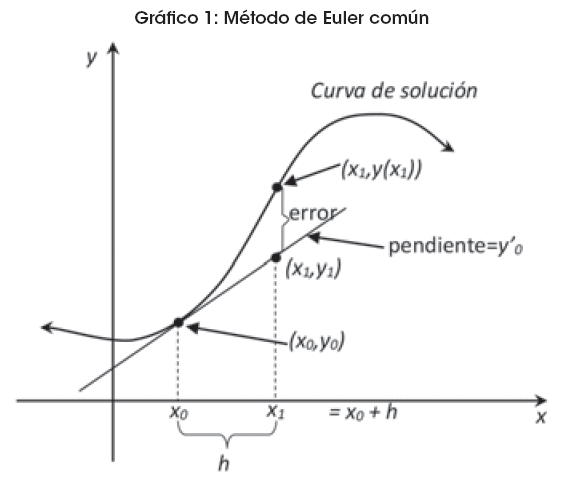
Por la fórmula de punto y pendiente de la ecuación de una recta se tiene:
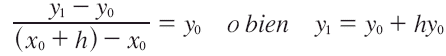
donde y0 = f(x0,y0). Si se denomina a x0+h como x1, entonces el punto (x1,y1) en la tangente es una aproximación al punto (x1,y(x1)) en la curva de solución; esto es y1 ≈ y(x1). Por supuesto, la precisión de la aproximación depende fuertemente del incremento h. Por lo común se debe seleccionar el tamaño de paso que sea "razonablemente pequeño".
Suponiendo un valor uniforme (constante) de h, puede obtenerse una sucesión de puntos (x1,y1), (x2,y2), ... , (xk,yk), los cuales es de esperar se encuentren cercanos a los puntos (x1,y(x1)), (x2,y(x2)), ... , (xk,y(xk)) (ver Gráfico 2).
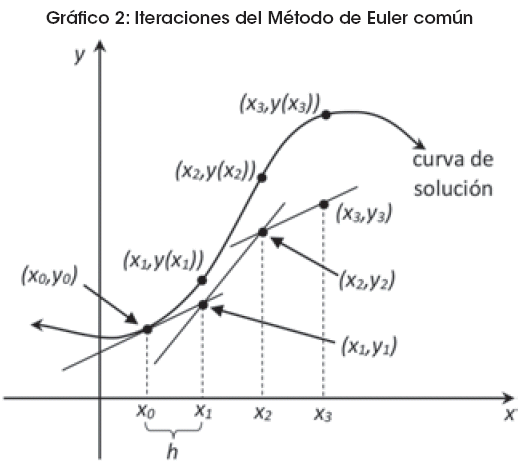
Ahora, utilizando (x1,y1) es posible obtener el valor de y2, el cual es la ordenada de un punto sobre una nueva recta "tangente". Se tiene así
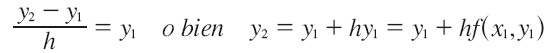
En general se deduce que:
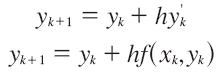
donde
![]()
De manera análoga, se puede deducir que:
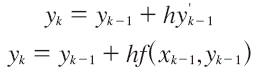
donde
![]()
La diferencia entre xk-xk-1 es h. Resolviendo la ecuación básica de Vartia se tendría:
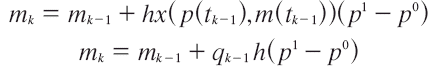
Para este caso, la diferencia entre tk-tk-1= h. Si se reemplaza dicha identidad en la diferencia de la "ruta" que conecta los precios se tendrá: p(tk)-p(tk-1 )=h(p1-p0), obteniendo la primera versión del algoritmo de Vartia.
![]()
Sin embargo, la solución bajo este método presenta errores de truncamientos locales y globales, como lo muestra Zill (2009). Dichos errores se dan porque en la sucesión de valores y1, y2, y3,... que son generados, el valor de y1 usualmente no concuerda con la solución real en x1, en particular, y(x1), porque el algoritmo sólo da una aproximación de línea recta a la solución. Esto ocurre en cada paso, es decir, si se supone que yk es precisa, entonces yk+1 tendrá error de truncamiento local. El error total en yk+1 es una acumulación de errores en cada uno de los pasos de iteración previos. Este error total se llama error de truncamiento global.
b) Método de Euler mejorado o fórmula de Heun
La fórmula:
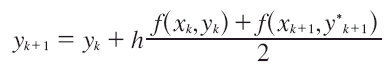
donde
![]()
se conoce como fórmula de Euler mejorada, o fórmula de Heun. Los valores f(xk ,yk) y f (xk+1, y*k+1) son aproximaciones a la pendiente de la curva en (xk,y(xk)) y (xk+1,y(xk+1)); en consecuencia, el cociente:
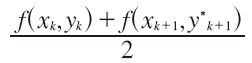
puede interpretarse como una pendiente promedio en el intervalo entre xk y xk+1.
Las ecuaciones de la fórmula de Heun pueden visualizarse fácilmente. En el Gráfico 3 se muestra el caso en que k=0.
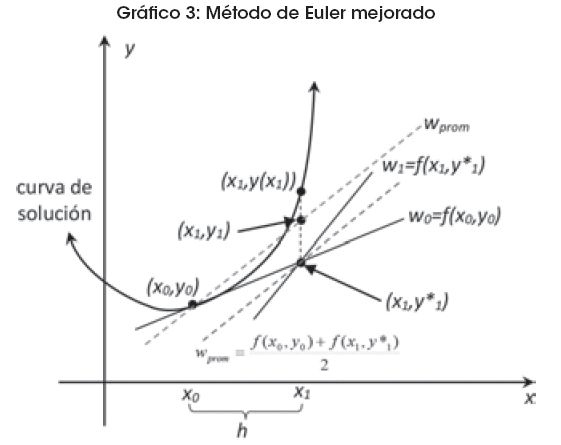
Obsérvese que:
![]()
son pendientes de las rectas que se indican, las cuales pasan por los puntos (x0,y0) y (x1,y*1), respectivamente. Tomando un promedio de estas pendientes, se obtiene la pendiente de las rectas oblicuas punteadas. En vez de seguirla recta de pendiente w = f(x0, y0) hasta el punto de ordenada y*1, obtenida mediante el método de Euler normal, se continúa la recta por (x0,y0) con pendiente wprom, hasta llegar a x1. Examinando el Gráfico 3 parece factible admitir que y1 es una mejora de y*1 Zill (1997) muestra que el método de Euler mejorado es más preciso que el método de Euler común5.
Además, podríamos decir que el valor de
![]()
predice el valor de y(x1), en tanto que
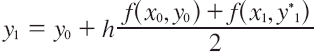
corrige esta estimación.
Una versión análoga de la fórmula de Heun es:
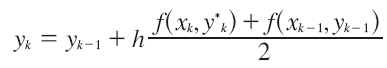
donde
![]()
Resolviendo una vez más la ecuación básica de Vartia se tiene:
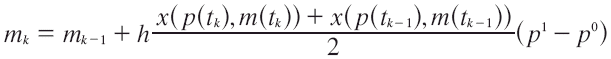
De la anterior sección se sabe que pk-pk-1 = h(p1-p0); entonces:
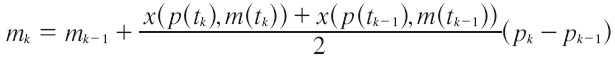
Realizando algunas operaciones, obtenemos nuevamente el algoritmo principal de Vartia6.
![]()
donde
![]()
4. Aplicación empírica
Habiendo determinado el marco conceptual para la evaluación de cambios del bienestar a partir de un enfoque microeconómico, en esta sección se realiza una aplicación empírica en un sector social, tal cual es la educación primaria en Bolivia, calculando la Variación Equivalente, inicialmente con el método de integrabilidad y posteriormente con el algoritmo de Vartia, a fin de verificar si este último puede reproducir los resultados de integrabilidad, sin necesidad de tener una especificación formal de la función de demanda por este servicio.
Se realiza únicamente el cálculo de la Variación Equivalente, debido a que se asume una disminución del 1% en el precio de la educación primaria; en tal sentido, definida una baja del precio a fin de garantizar un mayor bienestar a los hogares, es relevante el cálculo de dicha variación.
a) Estimación de la demanda por servicios de educación
Se estimó la demanda por educación utilizando la encuesta de hogares del año 2012, tomando únicamente el nivel primario. La unidad de análisis fue el hogar y las demandas estimadas consideraron datos mensuales, de cantidad, precio y la aproximación de ingreso. La cantidad de horas demandadas por educación primaria (q) fue aproximada con el número de horas que destinan los niños, por hogar, al asistir a la escuela. El precio de la educación (p) se aproximó a partir del gasto del hogar que se realiza en educación al año en cada miembro7 que recibe educación primaria; lo anterior incluye matrícula, pensiones, transporte, etc., elementos que permiten el acceso al niño o niña a la escuela.
El ingreso (m) debería estar constituido por el ingreso disponible que destina cada hogar en cada niño o niña; el criterio principal considerado es el cálculo del ingreso disponible por persona dentro del hogar, sin tomar en cuenta a los niños que van a primaria, debido a que ellos no deciden directamente si van o no ala escuela. Por los problemas de colinealidad entre variables, se considera el problema primal del consumidor, que consiste en maximizar un nivel de utilidad dado un nivel de precios e ingreso, es decir:

En este caso, z es una cesta de bienes que consume el individuo, y pT, un vector de precios. Entonces se puede decir para este caso en particular que el ingreso es:
![]()
o, de manera equivalente:
![]()
Donde p es el precio de la educación; q, la cantidad de demandantes por educación; potros un vector de precios de otros bienes; qotros, un vector de cantidades demandadas de otros bienes; y a, el ahorro o desahorro del individuo. Este criterio se incorporará en los modelos de demandas que se estiman en las siguientes secciones. Cabe resaltar que lo más relevante es la obtención de los parámetros a partir de las variables disponibles, y no al revés.
b) Modelo lineal de demanda
Si la función de demanda x(p, m) a estimar tiene la siguiente forma explícita:
![]()
donde β, α y γ son parámetros a estimar; є es el error de estimación, la principal dificultad es estimar; "γ" el ingreso de cada miembro del hogar, (m) no se encuentra en la encuesta de hogares. Sin embargo, a partir del criterio del problema primal del consumidor, se puede aproximar otra versión de la función de demanda como:
![]()
Reexpresando algunos términos se tiene:
![]()
Donde ε es el nuevo error de estimación. La estimación de la ecuación anterior genera un problema de multicolinealidad, por lo que muchas veces, dependiendo de cuán alta o baja sea esta, se recomienda no hacer nada al respecto. Claro está que este criterio se aplica por lo general si la multicolinealidad es baja; si la anterior expresión se estimara en una versión log-lineal, el coeficiente de determinación sería 1, presentando multicolinealidad perfecta y exacta, por lo cual es necesario realizar medidas correctivas.
Como se conoce la forma de la multicolinealidad, se estimará la siguiente ecuación:
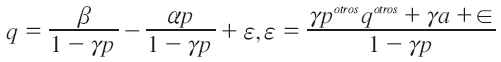
La estimación se debería hacer por mínimos cuadrados no lineales, definiendo inicialmente valores iniciales para los parámetros. Al existir la posibilidad de una baja convergencia, se optó por realizar dos estimaciones, siendo la ecuación auxiliar la siguiente:
![]()
Donde u = error de estimación de la ecuación auxiliar.
La ecuación auxiliar es reducible porque la dependiente (q) aún está presente en la variable dependiente (pq); reducirla significaría un modelo que dependa únicamente de p y q, olvidándonos del ingreso totalmente, así que en lugar de emplear (pq) como tal, se usó una variable proxy que es el ingreso disponible por persona del hogar (m_pc), sin tomar en cuenta a los niños en primaria8, obteniendo:
![]()
De dicha estimación se obtendrá el valor estimado para γ. Una vez obtenido dicho parámetro se estimó:
![]()
donde v es el error de estimación.
Los resultados de este modelo según departamento para la regresión auxiliar q = γm_pc + u son los que se presentan en el Cuadro 3.
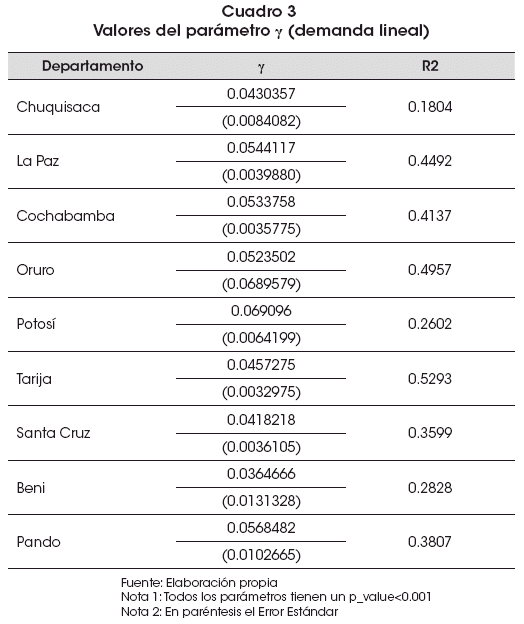
Los resultados de la estimación q_m= β – αp + v se presentan en el Cuadro 4:
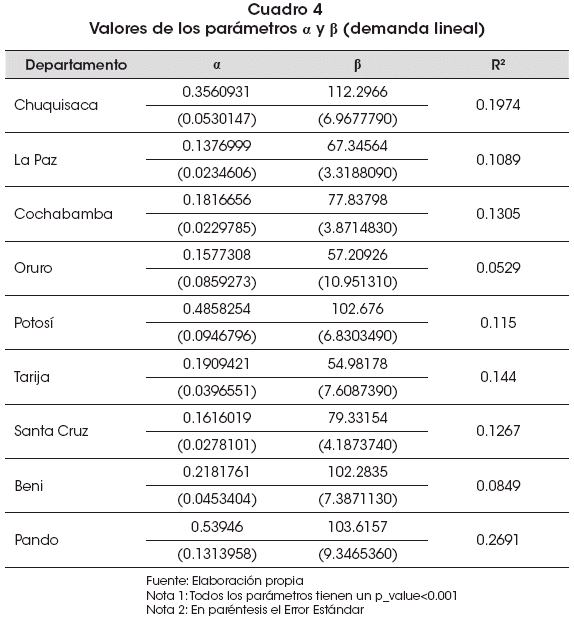
c) Modelo Log-Lineal de demanda
Si la función de demanda x(p,m) a estimar tiene la siguiente forma explícita:
![]()
Donde β, α e γ son parámetros a estimar; y є es el error de estimación, aplicamos logaritmos:
![]()
Bajo el criterio del problema primal del consumidor se tendría:
![]()
o
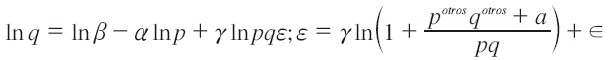
Donde ε es el nuevo error de estimación. En este caso en particular se tiene multicolinealidad perfecta y ajuste en un 100%; sin embargo, desarrollando dicha ecuación podemos obtener:
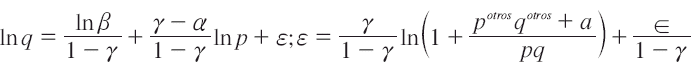
o
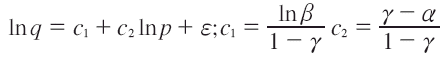
Surge otro problema, que es la estimación de dos parámetros reducidos c1 y c2, mientras se tienen como incógnitas los parámetros estructurales β, α e γ, imposibilitando la obtención de los parámetros estructurales; en consecuencia se tendrían dos ecuaciones con tres incógnitas. En tal sentido, se realizaron dos regresiones bajo el mismo criterio empleado en la estimación de la demanda lineal. La ecuación auxiliar fue especificada como:
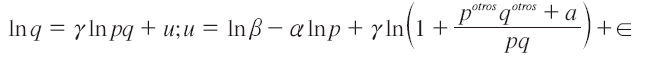
Dicha ecuación es aún reducible; dado que la variable dependiente (q) está presente en la independiente (pq), se usó una variable, el ingreso disponible por persona del hogar (m_pc), sin tomar en cuenta a los niños en primaria, obteniendo:
![]()
Donde u es error de estimación de la ecuación auxiliar. De dicha estimación se obtendrá el valor estimado para γ. Una vez obtenido dicho parámetro se estimó:
![]()
v es el error de estimación.
Los resultados por departamento para la regresión auxiliar ln q = γ ln m_pc + u; obtenidos con el modelo Log-Lineal de demanda se presentan en el Cuadro 5:
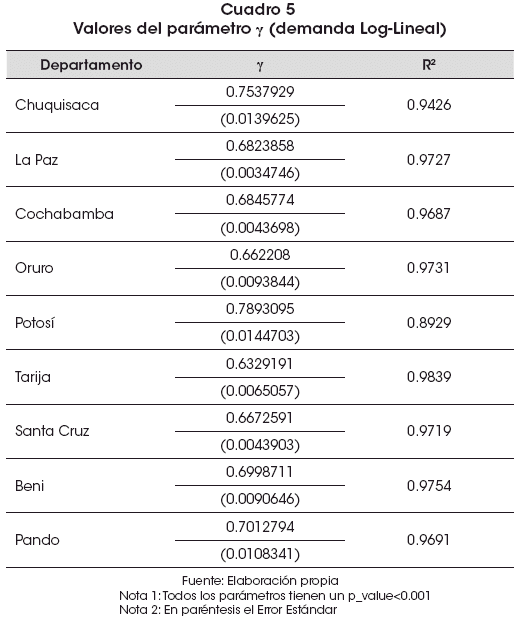
Los resultados de la estimación lq_m=ln β- α ln p+ v se presentan en el Cuadro 6:
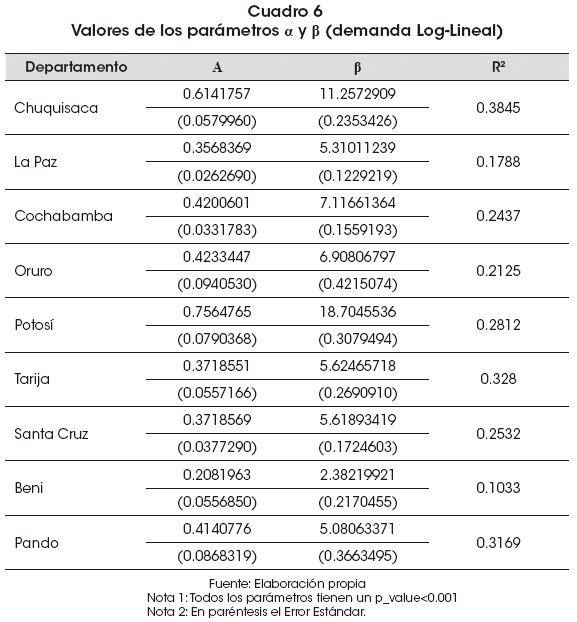
5. Estimación del bienestar en la educación primaria
a) El problema de la integrabilidad
Obtenidos los parámetros de las demandas especificadas para el cálculo de las variaciones equivalente y compensatoria mediante integrabilidad, recordemos que:
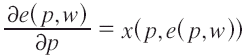
De acuerdo a la función de demanda lineal explícita definida anteriormente se tiene:
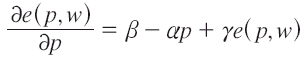
En términos de la función de ingreso compensada, sería:
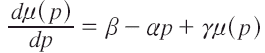
o
![]()
La ecuación diferencial anterior se puede resolver por coeficientes indeterminados (enfoque aniquilador)9. Por tanto, la función valor para esta demanda es:
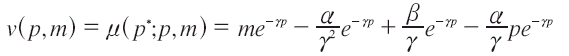
Para analizar la disposición a pagar dado un cambio de precios, lo relevante es analizar la pertinencia de una VC o VE; la variación compensatoria da o quita al individuo un monto de dinero a su ingreso para mantener la utilidad o bienestar a precios iniciales. Sin embargo, cuando se intenta mejorar el bienestar del individuo, ante un aumento del consumo de servicios de educación primaria debería bajar el precio, por tanto, no trata de mantener la utilidad o bienestar inicial, al contrario es una situación que trata de mantener un bienestar final o bienestar equivalente a una situación en la que se reduce el precio de la educación. La disposición a pagar más correcta de calcular sería, por tanto, una VE.
Calculando el bienestar a precios finales, tenemos:
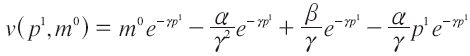
Éste debe igualar al bienestar a precios iniciales, ajustado vía ingreso, es decir, el ingreso inicial más el ajuste o disposición a pagar (m1 = m0+ VE). Por tanto, se tiene:
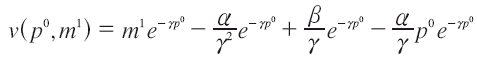
entonces:
![]()
Como ya se explicó, se sabe que m1 = m0+ VE, obteniendo:
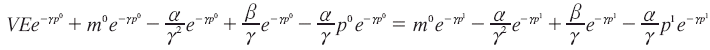
La VE sería entonces:
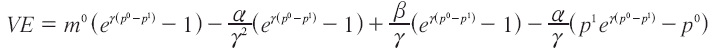
Para el caso de una demanda log-lineal tendríamos lo siguiente. Partimos de:
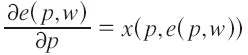
De acuerdo a la función de demanda log-lineal tenemos que:
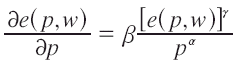
La función de ingreso compensada sería:
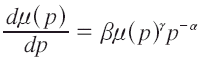
o
![]()
La anterior ecuación es una ecuación diferencial ordinaria de primer orden no lineal10. La función valor asociada para esta demanda es:
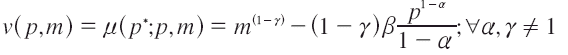
Si los parámetros α e γ son iguales a 1, la resolución se debe hacer por el método de Frobenious11. La función valor para este caso en particular es:
![]()
Suponiendo una disminución en el nivel de precios, nos interesa calcular la VE, por lo que, calculando el bienestar a precios finales, tenemos:
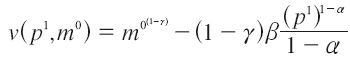
Este debe igualar con el bienestar a precios iniciales, ajustado vía ingreso, es decir, el ingreso inicial más el ajuste o disposición a pagar (m1 = m0 + VE). Por tanto, se tiene:
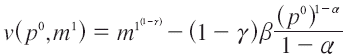
entonces:
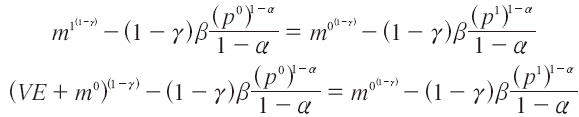
La VE sería:
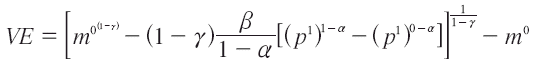
Empleando las especificaciones anteriores se procedió a realizar el cálculo de la Variación Equivalente para el sector primario de educación, suponiendo la presencia de una disminución del 1 % en el nivel de precios del servicio. Los parámetros β, α e γ se estimaron y son conocidos; el ingreso promedio mensual es Bs. 1.166,243. Este valor se aproximó a partir del monto promedio que recibe cada miembro del hogar del ingreso disponible total de cada hogar. Cabe resaltar como limitación que este monto supone una distribución dentro del hogar de manera igualitaria; no se consideró a los niños que asisten a primaria como miembros del hogar. Por otra parte, se asume que el precio o gasto promedio mensual de asistir a la escuela es aproximadamente Bs. 100.60. Con todos esos supuestos, los resultados para la Variación Equivalente, calculada mediante integrabilidad, con las dos especificaciones de la demanda, son los que se presentan en el Cuadro 7:
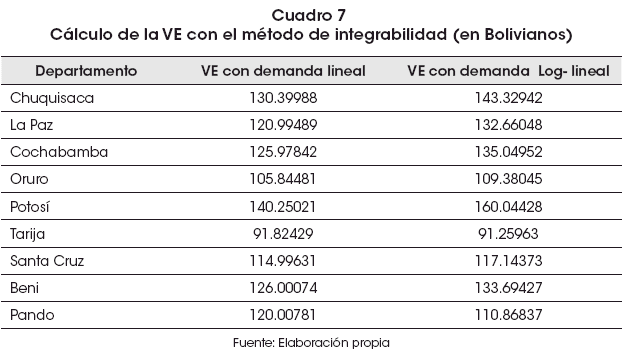
b) Algoritmo de Vartia
Para la aplicación empírica del algoritmo de Vartia, se programó el mismo y se realizaron 100.000 iteraciones, tomando en cuenta los parámetros estimados anteriormente. Nuevamente se asumió un ingreso promedio de Bs. 1.166, 243 y un gasto promedio escolar de Bs. 100,60.
Considerando una disminución del 1 % en el precio de la educación primaria, los resultados encontrados para la Variación Equivalente, tanto con una demanda lineal como con una log lineal, son los que se presentan en el Cuadro 8:
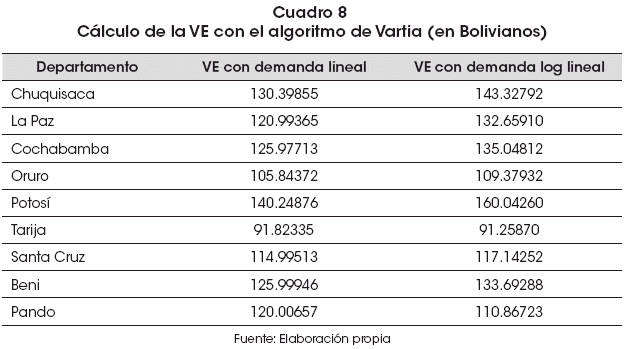
Contrastando estos resultados con los obtenidos mediante integrabilidad, se observan divergencias mínimas equivalentes al 0.001%, mostrando por tanto la fortaleza de esta metodología en lugar de la integrabilidad. Lo anterior respalda la idea de que este algoritmo puede ser una medida alternativa para el cálculo de cambios de bienestar, principalmente en sectores sociales, donde existen muchas complicaciones para la aproximación de funciones de demanda.
6. Conclusiones
Las metodologías de integrabilidad y el algoritmo de Vartia permiten aproximar cambios en el bienestar ante variaciones en los niveles de precio. Si bien ambas son parecidas en los resultados, dado que parten de un criterio de eficiencia, el nivel de flexibilidad de una frente a la otra no es trivial. El enfoque de integrabilidad exige que el investigador conozca la resolución de ecuaciones diferenciales, que cambia en función a la forma que tome la demanda. Si bien en este documento se trató de analizar diferentes modelos de demanda (lineal y log lineal), esto no quiere decir que éstas sean las únicas formas de comportamiento que pueda presentar la evidencia empírica, especialmente en sectores sociales como el de educación o salud. En contrapartida, el algoritmo de Vartia tiene una ventaja, traducida en la especificación "directa" de la función de demanda, sea cual sea su forma explícita. Si bien para aproximar la Variación Equivalente (o Variación Compensatoria) se requiere de varias iteraciones, al tener que programarse el algoritmo, las mismas pueden realizarse de manera factible y fehaciente. El cálculo de la Variación Equivalente en el sector de educación primaria en Bolivia, utilizando integrabilidad y el algoritmo de Vartia, permitió concluir que, para aproximar cambios de bienestar que responden a variaciones en los niveles de precio, el algoritmo de Vartia muestra mayor flexibilidad respecto del enfoque de integrabilidad.
Fecha de recepción: 22 de octubre de 2014
Manejado por: ABCE
Fecha de aceptación: 27 de mayo de 2015
Notas
* Economista, Ingeniero de sistemas, Profesor de la Carrera de Economía en la Universidad Católica Boliviana. Contacto: rrubin_de_celisc@ucb.edu.bo.
** Economista, Profesora de la Carrera de Economía en la Universidad Católica Boliviana. Contacto: lespinozav@ucb.edu.bo.
1 Ambas medidas del bienestar fueron introducidas por Hicks.
2 Para mayor detalle se recomienda revisar el teorema "Presupuesto equilibrado y simetría Implica homogeneidad'.
3 La expresión de "alguna forma" se refiere al hecho de que en las ecuaciones diferenciales, sean éstas ordinarias o no, existen diversas técnicas para poder encontrar la solución. No existe un único método de resolución.
4 Integrando la ecuación anterior se tiene:
5 No se detallarán las diferencias de ambos métodos, sin embargo, se recomienda revisar la sección 9.6 de Zill (1997), el cual trata sobre errores y estabilidad.
6 En el paper de Vartia (1983) se realizan otras consideraciones para los valores iniciales. Para entender con mayor precisión estos detalles se recomienda revisar el documento original.
7 No es el total del gasto del hogar en educación primaria, sino lo que se gasta de manera individual.
8 Es probable que m_pc recoja el efecto del gasto en otros bienes.
9 Se recomienda ver el capítulo de ecuaciones diferenciales lineales de orden superior, en Zill (1997).
10 Se recomienda ver el capítulo de ecuaciones diferenciales de primer orden, en Zill (1997).
11 Se recomienda ver el capítulo de ecuaciones diferenciales con coeficientes variables, en Zill (1997).
Referencias
1. Border, KC. (2003). "The Integrability Problem". Division of the Humanities and Social Sciences. California Institute of Technology [ Links ]
2. Breslaw, Jon A. y Smith, J. Barry. (1995). "A Simple and Efficient Method for Estimating the Magnitude and Precision of Welfare Changes". Journal of Applied Econometrics, 10, 313-327.
3. Jehle, Geoffrey A. y Reny Philip J. (2011). Advanced Microeconomic Theory. Tercera edición. Pearson.
4. Mendieta, Juan Carlos. (2007). "Economía de bienestar aplicado". Notas de Clase. Facultad de Economía. Universidad de los Andes. [ Links ]
5. Varian, H. (1998). Análisis microeconómico. Tercera edición. Barcelona, España: Antoni Bosch.
6. Vartia, Yrjö O. (1983). "Efficient methods of measuring welfare change and compensated income in terms of ordinary demand functions". Econometrica, 51 (1), 79-98. [ Links ]
7. Zill, Dennis G. (1997). Ecuaciones diferenciales con aplicaciones. Tercera edición. México: Grupo Editorial Iberoamérica.
8. ---------- (2009). Ecuaciones diferenciales con aplicaciones de modelado. Novena edición. México: Cengage Learning Editores.