Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Latinoamericana de Desarrollo Económico
versión impresa ISSN 2074-4706versión On-line ISSN 2309-9038
rlde n.16 La Paz nov. 2011
Hodrick-Prescott, Goodwin y ciclos económicos en Bolivia
Hodrick-Prescott, Goodwin and Business Cycles in Bolivia
Horacio Villegas Quino a , Raúl Rubín de Celis b , Javier Aliaga Lordemann c
Resumen
Los ciclos económicos no tienen un comportamiento idéntico en el corto y largo plazo, mostrando que no existe equilibrio ni de corto ni largo plazo. La causa principal de la inestabilidad es la incidencia de las fuerzas exógenas en la economía doméstica. Un posible aumento de estas fuerzas exógenas hace que los ciclos del producto sean cada vez más inestables.
La interacción del acelerador con la propensión marginal a ahorrar y el tiempo que se dedica a la producción de nuevos bienes de capital y consumo, pueden minimizar el efecto de las fuerzas exógenas. La interacción anteriormente mencionada se la puede aproximar como el ambiente de la inversión; cuanto más alta ésta sea, mayor será la posibilidad de reducir posibles choques externos.
Palabras clave: Ciclos económicos, equilibrio, estabilidad, corto plazo, largo plazo, acelerador, no linealidad, inestabilidad, caos.
Abstract
Business cycles do not show identical behavior in the short and the long term, evidencing that there is no equilibrium. The main cause of instability is the incidence of exogenous forces on the domestic economy. A possible increase of these exogenous forces causes more instability in the cycles of the product.
The interaction between the accelerator and the marginal propensity to save, and the time devoted to the production of new capital goods and consumption, can minimize the effect of exogenous forces. The interaction mentioned above can be approximated as the investment environment; the higher this is, the greater the possibility of reducing external shocks.
Keywords: Bussines Cycles, Equilibrium, Stability, Short run, Long run, accelerator, nonlinearity, instability, chaos.
Clasificación/Classiffication JEL: C62, E32
1. Introducción
El descubrimiento de que ciertos fenómenos de dinámica económica, en particular los ciclos persistentes (continuos), no pueden ser enfrentados efectivamente por medio de modelos lineales, ha llevado a un creciente número de investigadores a hacer uso de métodos de análisis no lineal. Según Navarro (2002), esto es necesario para un profundo entendimiento del comportamiento complejo de sistemas dinámicos. Equilibrio estable e inestabilidad, incluso ciclos límites, son revelados ahora, más que como una configuración, en un más rico y complejo universo teórico. Tan pronto como la linealidad ha sido dejada, incluso un modelo simple puede mostrar un comportamiento muy complicado.
Encontrar causalidad entre series puede ser, en algunos casos, bastante simple; pero el análisis no lineal permite una mejor aproximación entre algunas variables. Es decir que la causalidad y los supuestos de muchos modelos pueden ser bastante aceptables, pero la forma de aproximación de estos modelos a una forma lineal, limita el análisis y puede llevar a teorías equivocadas.
Goodwin (1951) desarrolló un modelo no lineal, enfatizando la importancia de la inversión como generador de ciclos económicos. El modelo de Goodwin tiende a ser estable a pesar de ser no lineal. Recientemente Chian (2007) se basa en Lorenz y Nusse, los cuales reconstruyen el modelo y muestran que el caos está presente en el modelo, y éste es alto en la medida que la no linealidad del modelo es elevada. Por ello, este documento analizará los ciclos económicos en Bolivia a partir de estas nuevas consideraciones al modelo de Goodwin. Cuantificará los parámetros y obtendrá los ciclos mediante el filtro Hodrick-Prescott, y predecirá el comportamiento de éstos en la economía boliviana.
2. Modelo de Van der Pol forzado de ciclos económicos no lineales
Goodwin (1951) definió una ecuación oscilatoria sobre el producto y la inversión:
![]()
donde y(t) es el ingreso, α es la propensión marginal a consumir, φ(y) refleja las decisiones de inversión, 0 * (t) estaría compuesto por variables exógenas en el periodo t + θ , ![]() es el tiempo en que se tarda en producir nuevos bienes de consumo y θ es el tiempo que se tarda en la fabricación de bienes de capital. Los valores de
es el tiempo en que se tarda en producir nuevos bienes de consumo y θ es el tiempo que se tarda en la fabricación de bienes de capital. Los valores de ![]() y θ están expresados en años.
y θ están expresados en años.
Chian (2007) y Matsumoto (2007) mencionan a Lorentz, Lorenz y Nusse que consideraron la siguiente generalización de la ecuación (1), la cual suponía un comportamiento caótico en el multiplicador acelerador no lineal de Goodwin.
![]()
donde A(x) es una función par (even function) con A(0) < 0, y B (x) es una función impar (odd function) con B (0) = 0. Asumiendo que los gastos de inversión son una función periódica y continua del tiempo:
![]()
donde α es la amplitud de la fuerza exógena y w la frecuencia de la fuerza exógena, y
![]()
Obtenemos un modelo de Van der Pol forzado de ciclos económicos no lineales.
![]()
De acuerdo a estas consideraciones, se podría aproximar la ecuación (1) a la siguiente expresión:
![]()
Asumiremos que α sin(wt + b) es el componente no lineal de la tendencia del producto, donde α está compuesto por fuerzas exógenas (exogenous forces), w es la frecuencia de dicha fuerza exógena y b refleja el periodo en el cual comienza dicha fuerza exógena.
Aproximando (6) a la ecuación de Van der Pol se tiene:
![]()
donde v es el acelerador no lineal.
3. Modelo econométrico
La tendencia Hodrick-Prescott es una tendencia no lineal. Por tanto, una manera de expresar dicha tendencia puede ser:
![]()
donde yhp es la tendencia Hodrick-Prescott, c + γt es la tendencia lineal y NLT es el componente no lineal de la tendencia Hodrick-Prescott. Se debe tratar de aproximar NLT a una forma funcional. De acuerdo a las ecuaciones (6) y (7), NLT sería:
![]()
4. Resultados
En Aliaga, Rubín de Celis y Villegas (2011) se muestran los siguientes resultados para α, ![]() y θ:
y θ:
Cuadro 1
Parámetros en su forma estructural del modelo de Goodwin
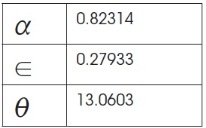
Fuente: Elaboración propia
Asimismo, la estimación del acelerador se detalla en el siguiente cuadro:
Cuadro 2
Acelerador no lineal del modelo de Goodwin
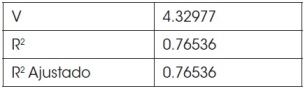
Fuente: Elaboración propia
4.1. Componente no lineal
El cálculo del componente no lineal se lo realizó a partir de la expresión (8) a través de una regresión lineal, para así poder obtener el componente no lineal. La serie NLT presenta problemas de raíz unitaria, por tanto la expresión (9) se tuvo que diferenciar dos veces para poder usar variables estacionarias en la regresión.
Cuadro 3
Parámetros del componente no lineal de la tendencia
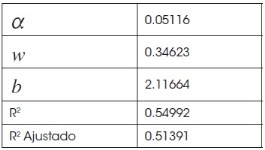
Fuente: Elaboración propia
4.2. Ciclos límite y ciclos económicos
Los ciclos límite nos permiten analizar la estabilidad del modelo. Tradicionalmente la estabilidad estaba dada por la coexistencia de múltiples ciclos económicos, y saber cuáles eran estables o no era posible a través de la bifurcación de Hopf. Debido a la presencia de este componente no lineal, se podría decir que éste distorsiona de manera significativa la estabilidad del modelo.
Se graficó el ciclo límite y los ciclos económicos para Bolivia a partir de la ecuación (7). Las condiciones iniciales que se establecieron se obtuvieron a partir los ciclos obtenidos por el filtro Hodrick-Prescott. Los valores de z(0) corresponden al año 2009 y z'(0) es la diferencia entre el año 2009 y el año 2008.
Gráfico 1: Ciclo límite
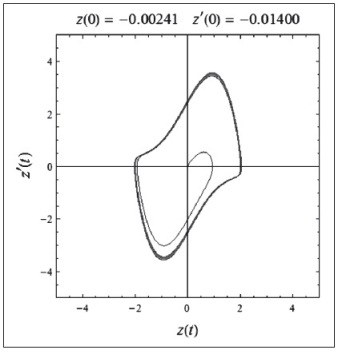
Fuente: Elaboración propia
Gráfico 2: Ciclos económicos
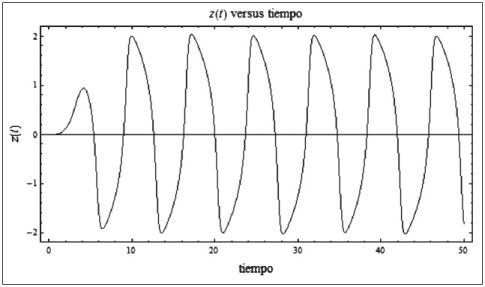
Fuente: Elaboración propia
Sin embargo, existe una sobredimensión de z'(0), por lo que es necesario reducir el valor de z'(0).
Gráfico 3: Ciclo límite con variación menor de z'(0)
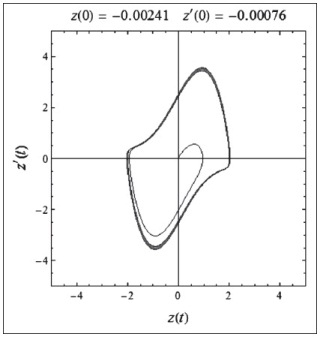
Fuente: Elaboración propia
Gráfico 4: Ciclos económicos con variación menor de z'(0)
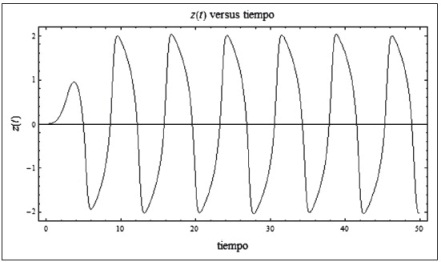
Fuente: Elaboración propia
Los casos anteriores muestran una solución inestable, es decir que se observan desvíos en las trayectorias de los ciclos límite. La solución es inestable y se observa de mejor forma en los ciclos límite; una solución estable se da cuando la fuerza exógena es igual a cero. Al ser diferente de cero, ésta es inestable, aunque no caótica. Para ejemplificar de mejor manera se amplía el valor de las fuerzas exógenas y se puede advertir el comportamiento inestable, como se muestra a continuación.
Gráfico 5: Ciclos límite con un valor mayor a 0.05 de las fuerzas exógenas
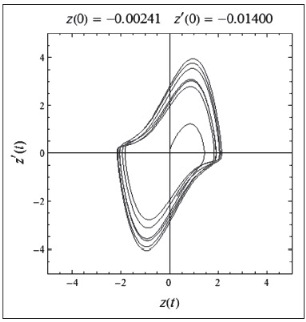
Fuente: Elaboración propia
Gráfico 6: Ciclos económicos con un valor mayor a 0.05 de las fuerzas exógenas
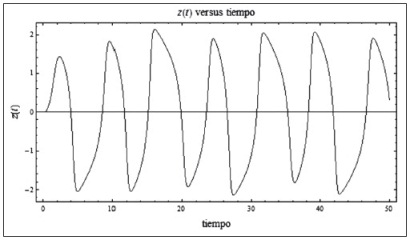
Fuente: Elaboración propia
Esta ejemplificación confirma las primeras dos situaciones de ciclos límite y ciclos económicos mencionados con anterioridad, confirmando la inestabilidad de los ciclos económicos.
5. Conclusiones
La complejidad en el análisis de los ciclos económicos se da sobre todo por la presencia de una tendencia no lineal, como es la tendencia Hodrick-Prescott. Los ciclos económicos no tienen un comportamiento idéntico en el corto y largo plazo, mostrando que no existe equilibrio de corto y largo plazo. La causa principal de la inestabilidad es la incidencia de las fuerzas exógenas en la economía doméstica. Un posible aumento de estas fuerzas exógenas hace que los ciclos del producto sean cada vez más inestables.
La interacción del acelerador con la propensión marginal a ahorrar y el tiempo que se dedica a la producción de nuevos bienes de capital y consumo pueden minimizar el efecto de las fuerzas exógenas. La interacción anteriormente mencionada se la puede aproximar como el ambiente de la inversión; cuanto más alta sea ésta, mayor será la posibilidad de reducir posibles choques externos.
En Bolivia, el ambiente de inversión es bajo con respecto a la incidencia de las fuerzas exógenas, porque estas últimas logran distorsionar el equilibrio de corto y largo plazo.
Artículo recibido en: enero de 2011
Manejado por: ABCE
Aceptado en: julio de 2011
Referencias
1. Ackley, Gardner. (1970). Teoría macroeconómica. México: The Macmillan Company. 1° Ed. Unión Tipográfica. Editorial hispano-americana. [ Links ]
2. Aliaga, J.; Rubín de Celis, Raúl y Villegas Quino, Horacio. (2011). El modelo de Goodwin. Ciclos económicos e inversión en Bolivia. Revista Latinoamericana de Desarrollo Económico, N° 15 Universidad Católica Boliviana San Pablo [ Links ]
3. Chian, Abraham C.L. (2007). Complex Systems Approach to Economic Dynamics. Berlin: Springer-Verlag. [ Links ]
4. Chiang, Alpha C. (1996). "Métodos fundamentales de economía matemática". 3º Ed. Madrid: McGraw-Hill. [ Links ]
5. Costain, James. (2005). Apuntes sobre PIB y hechos estilizados. Universidad Carlos III de Madrid. [ Links ]
6. Hodrick, Robert y Prescott, Edward C. (1997). Postwar U.S. Business Cycles: An
Empirical Investigation. Journal of Money, Credit, and Banking, 29 (1): 1-16.
7. Goodwin, R. M. (1951). The Nonlinear Accelerator and the Persistence of Business Cycles. Econometrica, 19: 1-17.
8. Greene, William. (2002). Econometric Analysis. 5° Ed. Prentice Hall.
9. Maravall, Agustín, y del Río, Ana. (2001). Time Aggregation and the Hodrick-Prescott Filter. Banco de España. [ Links ]
10. Maravall, Agustín y del Río, Ana. (2007). Temporal Aggregation, Systematic Sampling, and the Hodrick-Prescott Filter. Banco de España. [ Links ]
11. Matsumoto, Akio y Suzuki, Mami. (2006). Coexistence of Multiple Business Cycles in Goodwin's 1951 model. The Institute of Economic Research. Chuo University.
12. Matsumoto, Akio. (2007). Note on Goodwin's 1951 Nonlinear Accelerator Model with an Investment Lag. The Institute of Economic Research. Chuo University. [ Links ]
13. Navarro, Jesús. (2002). No linealidad y dinámica económica: algunos comentarios ". Revista venezolana de análisis de coyuntura. Universidad Central de Venezuela. [ Links ]
14. Zhang, W. (2005). Differential Equations, Bifurcations, and Chaos In Economics. World Scientific Publishing Co. Pte. Ltd. [ Links ]
a Investigador senior y administrador del proyecto CELA del Instituto de Investigaciones Socio Económicas (IISEC) de
b Investigador asociado del Instituto de Investigaciones Socio Económicas (IISEC) de
c Director del Instituto de Investigaciones Socio Económicas (IISEC) de














