Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Latinoamericana de Desarrollo Económico
versión impresa ISSN 2074-4706versión On-line ISSN 2309-9038
rlde n.15 La Paz mayo 2011
ARTICULO ORIGINAL
Análisis y pronóstico de la demanda de potencia eléctrica en Bolivia: una aplicación de redes neuronales
Power Electric Demand in Bolivia Analysis and projection: A Neuronal Network Application
Gimmy Nardó Sanjinés Tudela *
*Investigador del Instituto de Investigaciones Socio Económicas (IISEC-UCB). La Paz–Bolivia. g_sanjinez_t@ucb.edu.bo
Resumen
El objetivo del presente trabajo de investigación es analizar la demanda de energía eléctrica en Bolivia con base en el pronóstico de series de tiempo. La predicción de datos futuros desde la perspectiva económica es importante porque se utiliza para optimizar la asignación de la energía en el tiempo, bajo la premisa de que cualquier mejora en la disminución del error de pronóstico representa una mejora en el excedente del consumidor. El pronóstico, por su complejidad, es realizado básicamente mediante cuatro fases; modelos armónicos, modelos Arima x Sarima, modelos Arma-Garch y finalmente modelos con base en redes neuronales artificiales. Los resultados muestran que el mínimo error se logra utilizando redes neuronales artificiales, y finalmente se concluye que el beneficio económico por la implementación de los modelos de redes neuronales artificiales en la predicción de la demanda de potencia eléctrica se presenta por la reducción de los costos incrementales generados por el error de pronóstico.
Palabras clave: Demanda eléctrica, asignación energética, inteligencia artificial, redes neuronales artificiales, modelado en espacio de frecuencias, pronóstico, Modelos Arima x Sarima, Modelos Arma-Garch, estimación de número de armónicas, transformada de Fourier.
Abstract
The objective of this research is to analyze the demand for electricity in Bolivia, based on time series forecasting. The prediction of future data from the economic perspective is important because it is used to optimize the power allocation over time under the premise that any improvement in forecast error reduction is an improvement in consumer surplus. The prognosis for its complexity is done primarily through four phase’s harmonic models, models Arima x Sarima, Arma-Garch models and finally models based on Artificial Neural Networks. The results show that the minimum error is achieved using artificial neural networks and finally concluded that the economic benefit from the implementation of artificial neural network models in predicting the electrical power demand is presented by the reduction of incremental costs generated by the forecast error.
Keywords: Electrical demand, Allocation Energetics, Artificial intelligence, Artificial Neuronal Networks, Modeled in Space of Frequencies, Forecast, Models Arima x Sarima, Arma - Garch Models, Estimation of Number of Harmonicas, Transformed of Fourier.
Clasificación / Classification JEL: C45, Q41
1. Introducción
La energía eléctrica es un recurso esencial que forma parte de las actividades del ser humano, por esto es de especial interés, tanto para las autoridades que regulan el sector eléctrico como para las empresas involucradas en este sector, que el manejo del recurso sea eficiente. Dada la importancia del sector, los elementos que se deben manejar son la planeación, la asignación y la minimización de costos. Esto es necesario para lograr un uso racional del recurso buscando la sustentabilidad (García, 2010).
La planeación, como pilar fundamental, involucra generalmente el pronóstico del nivel de demanda como base para la oferta del sistema y la creación de políticas y normas, logrando de esta manera el óptimo desempeño del sistema; de manera indirecta se busca que los usuarios finales del recurso posean conciencia y educación para su uso.
El Comité Nacional de Despacho de Carga (CNDC) es la institución encargada de la planificación y la operación del Sistema Interconectado Nacional de Bolivia, y el administrador del mercado eléctrico mayorista.
El CNDC fue creado por la Ley Nº 1604 (Ley de Electricidad) del 21 de diciembre de 1994. Es una persona jurídica pública, no estatal y sin fines de lucro; su domicilio legal es la ciudad de Cochabamba. Sus actividades, que se desarrollan desde febrero de 1996, estuvieron supervisadas por la Superintendencia de Electricidad hasta abril de 2009; a partir de esa fecha está sujeta a la supervisión de la Autoridad de Fiscalización y Control Social y del Ministerio de Hidrocarburos y Energía.
El CNDC es responsable de coordinar la operación de la generación, transmisión y expansión óptima del Sistema Interconectado Nacional, de realizar el despacho de carga a costo mínimo y de la administración del mercado eléctrico mayorista, de acuerdo con los lineamientos del Ministerio de Hidrocarburos y Energía.
Para alcanzar el propósito de minimización de costos en su actividad de distribución de energía, el CNDC requiere de instrumentos que le permitan lograr pronósticos insesgados y de mínima varianza en intervalos de horas. Estos pronósticos viabilizarían acopiar de las empresas generadoras de energía el requerimiento de la tensión necesaria en sus redes para satisfacer los requerimientos de los centros urbanos y centros productivos.
Con base en lo anteriormente expresado, el objetivo de la presente investigación es proveer de métodos e instrumentos que posibiliten describir el patrón de comportamiento de la demanda, y finalmente el pronóstico.
2. Pronóstico de potencia eléctrica
El pronóstico de la demanda de potencia o carga es fundamental en cualquier problema de toma de decisiones sobre un sistema eléctrico, y es, por tanto, una de las actividades básicas en la planificación. Para estudios de planeamiento de largo plazo, el pronóstico de demanda debe considerar horizontes que pueden variar entre cinco y veinticinco años, dependiendo del horizonte de planeamiento, y puede abarcar un área geográfica a escala local o nacional. La determinación del área geográfica depende de si requiere el planeamiento de generación, transmisión o distribución. Asimismo, el pronóstico de demanda puede referirse a la potencia pico, a la energía total demandada o al comportamiento de la curva de carga (García y Cabrera, 2003).
En el presente trabajo, la demanda de potencia de corto plazo se refiere a la curva de carga diaria o demanda de potencia horaria, y se plantea para realizar pronósticos a nivel nacional. El pronóstico en el corto plazo de la potencia tiene como objetivo el manejo eficiente y asegurar la operatividad del sistema eléctrico, optimizando el despacho económico horario.
El despacho económico de carga es una de las más importantes funciones dentro del mercado mayorista de electricidad, el cual se debe realizar para garantizar el suministro de energía, maximizando la seguridad del sistema interconectado nacional, y minimizando los precios mayoristas en el mercado horario de energía. Para ello la CNDC elabora el plan de despacho, en el que prevé asignar la producción a los generadores más económicos, según la declaración de costos que éstos hacen al CNDC. Asimismo, dada la naturaleza de la energía eléctrica, que hace que la misma deba ser producida en el preciso momento en que es requerida por los consumidores, debe hacerse un seguimiento continuo, llamado operación en tiempo real, que tiene como finalidad verificar el cumplimiento del programa de despacho y tomar de manera inmediata las acciones necesarias para afrontar las desviaciones que surgen respecto del mismo, tales como el aumento o disminución de la demanda de energía, siempre buscando minimizar los costos de operación y maximizando la seguridad del suministro.
Para llevar a cabo el despacho económico horario, las empresas distribuidoras y comercializadoras de energía deben proporcionar al CNDC el pronóstico de la demanda de potencia diaria de la región a la cual le suministra la carga. Una vez recibidos los pronósticos de demanda de potencia del país y las ofertas de potencia para cada una de las horas del día de las empresas generadoras, el CNDC se encarga de elaborar el programa horario de generación de los recursos del sistema interconectado, bajo criterios de eficiencia económica y técnica.
Se muestra en el Cuadro 1 la participación de las empresas en la satisfacción de demanda por potencia eléctrica, tomado en cuenta las empresas reguladas y no reguladas.
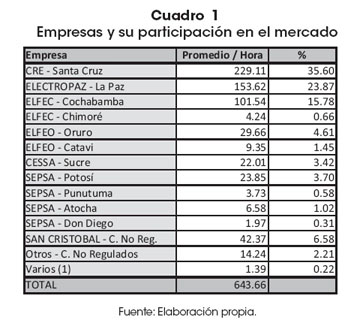
Con base en la descripción de la problemática abordada se procede a plantear la metodología y secuencia de la aplicación, las mismas que se muestran y aplican en los siguientes acápites.
3. Planteamiento metodológico
La presente investigación comprende la realización de las siguientes fases o componentes para el logro del objetivo:
- Acopio de los datos y sistematización
- Análisis espectral e interpretación de resultados
- Modelado lineal y análisis de resultados
- Diagnóstico de no linealidad
- Modelado no lineal y análisis de resultados
- Estructuración y entrenamiento de la red neuronal artificial
- Diagnóstico del mejor experto y pronóstico
- Análisis de resultados
4. Análisis, modelado y pronóstico de la potencia demandada (horas-día)
Graficar, observar y analizar el comportamiento de los datos es la primera y más importante herramienta en el análisis de series de tiempo. Esto permite concebir la complejidad de la evolución a modelar. Es por esta razón que se inicia el análisis graficando los 5204 datos horarios que conforman la serie real (Gráfico 1); en la misma se muestra el comportamiento de la demanda de potencia total (expresada en MW) abastecida por las diferentes empresas en los meses de diciembre 2009 a julio 2010.
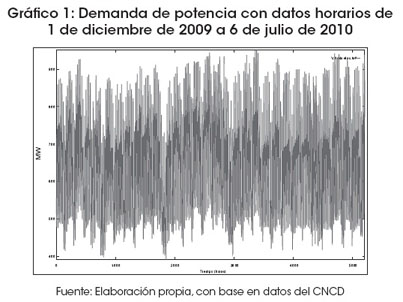
Para realizar el análisis del comportamiento de demanda diario se hace uso del análisis espectral, que comprende dos fases; la primera, el análisis mediante la transformada de Fourier, y la segunda, el modelado mediante modelos no lineales armónicos. El presente análisis se realiza porque en este punto se presume la existencia de ciclos y/o estacionalidades al interior de la serie. Asimismo, se puede afirmar que cada hora se incrementa, en promedio, un 0.002 MW la demanda de potencia.
La transformada de Fourier consiste en transformar los datos del espacio del tiempo al espacio de las frecuencias, resultado que demuestra la existencia de periodicidades o patrones periódicos.
En otras palabras, se trata de muestrear la función cuya transformada se desea conocer, de tal modo que el intervalo del muestreo nos defina la longitud de onda de Nyquist. Esta última debe ser resultado de una estimación de la máxima frecuencia existente en la función buscada.
La estimación empírica de la transformada de Fourier se realiza utilizando las siguientes ecuaciones:
Función par: Sea f(x) una función par, entonces, la transformada de Fourier es:
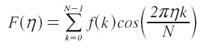
Función impar: La función buscada es imaginaria y está dada por:
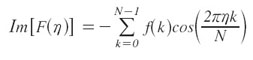
La aplicación de la mencionada transformación se muestra en el Gráfico 2.
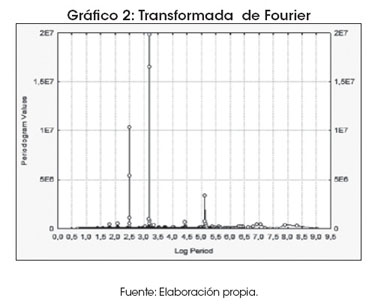
Con base en los resultados obtenidos que se observan en el Gráfico 2, se menciona que la demanda de potencia, analizada con datos horarios, muestra un comportamiento estacional con por lo menos dos periodicidades diarias y al menos una semanal. Es decir, existen, al interior de la serie, frecuencias significativas correspondientes a las 10 horas, 20 horas y 168 horas. Las dos primeras se explican porque existen dos o más armónicas inmersas durante las 24 horas de demanda de potencia y la tercera corresponde a la existencia de al menos un ciclo semanal en el patrón de consumo.
Dados los resultados obtenidos, se procede a modelar estos patrones cíclicos mediante modelos no lineales armónicos. El análisis armónico corresponde al modelado no lineal con base en la composición de funciones senoidales y cosenoidales, como se expresa de manera formal en la siguiente ecuación:
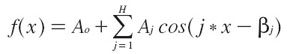
Donde :
0<x<2<π
H: número máximo de armónicas
Aj: Amplitud j
Bj: Fase j
A continuación se muestra el modelo generado para los datos promediados diarios (en el siguiente: orden martes, miércoles, jueves, viernes, sábado, domingo y lunes); luego se muestran en el Gráfico 3 los datos reales y estimados por el modelo.
![]()
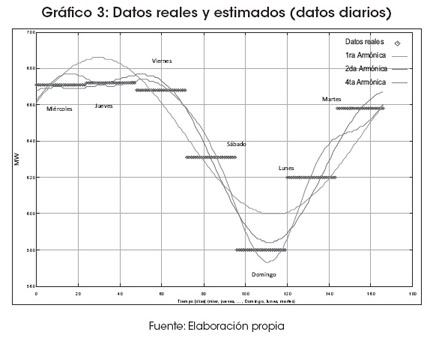
Dados los resultados del modelo, se puede diagnosticar un modelo con segunda armónica con datos promediados semanales. El modelo muestra un máximo consumo los días miércoles, jueves y viernes, y un mínimo el día domingo. Esto es corroborado por la existencia de una primera amplitud de 43.13 y una segunda de 15.45, con un desfase de -1 y -5.02.
Realizando el mismo análisis para los promedios de demanda de potencia hora-día, se afirma que la mínima demanda promedio se localiza entre las 3 y 4 de la mañana y la máxima de 7 a 8 de la noche; se puede también mencionar que existe un segundo consumo máximo, de 10 a 12 en el mediodía. Esta interpretación se acompaña mediante el modelo estimado y el Gráfico 4.
![]()
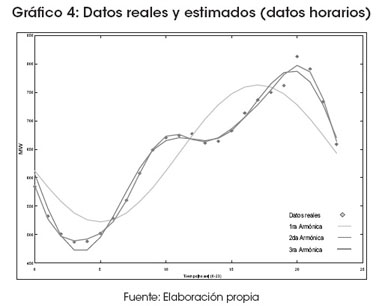
Realizado el análisis espectral, se puede concluir que en la serie temporal se tienen dos componentes cíclicos, uno correspondiente al día y otro a la semana. Los ciclos nos ayudan a comprender que existen demandas diferenciales entre día y noche, fines de semana y semana de trabajo. Patrones más importantes a la hora de realizar los pronósticos.
A continuación se estiman los parámetros para modelos lineales ARIMA (p,d,q) x SARIMA(P,D,Q).
El principio básico del modelado de series de tiempo es la construcción de un “filtro” lineal, el cual genere, por un lado, el modelo del patrón lineal, y, por otro, ruido blanco. Estos modelos tienen la forma:
![]()
Donde:

La ventaja en estos modelos es que la estimación de parámetros es relativamente sencilla, pero su debilidad yace en la adaptabilidad. En general el pronóstico realizado con este tipo de modelos es conservador, porque tienden a la media de manera exponencial y evitan los valores extremos, que son en realidad los que se requiere predecir.
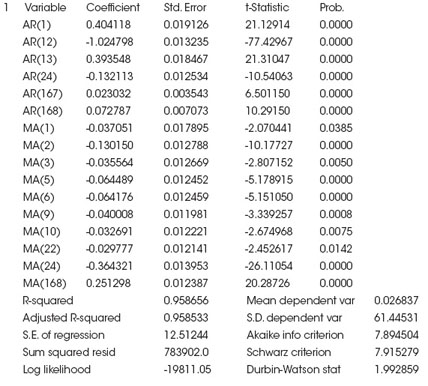
El modelo matemático diagnosticado remplazando los parámetros estimados es el siguiente1:
![]()
Las estimaciones se realizan con datos que poseen una desintegración de primer orden y otra de orden 24 estacional, la misma que se empleó con base en la información del análisis espectral.
El modelo muestra básicamente el componente estacional, el cual se demuestra mediante los parámetros correspondientes al modelo SARIMA.
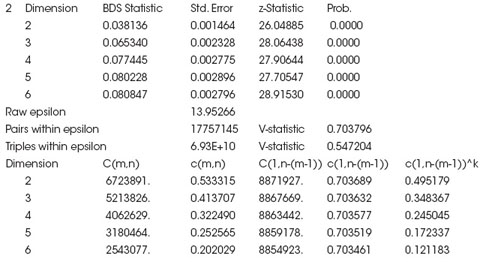
Luego de realizado el modelado lineal se pasa a buscar patrones no lineales, para lo cual se hace uso de la prueba dada por Brock, el cual por su robustez es utilizado para detectar patrones de comportamiento no lineal.
La presente prueba contrasta la hipótesis nula de independencia e idénticamente distribuidas para series de tiempo x(t) mediante el uso de la correlación espacial. Para examinar esta correlación espacial, la serie de tiempo debe llevarse a un m-espacio, para construir el siguiente vector:
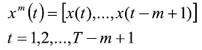
En este caso, la transformación a diferentes espacios o dimensiones crea nuevos vectores en sus respectivas dimensiones. Así, esta transformación permite tomar datos de la serie temporal y transformarlos a un espacio dimensional superior. La motivación detrás de esto es examinar la correlación en un contexto hiperespacial.
La dependencia de x(t) es examinada a través del concepto de correlación integral, una medida que examina las distancias entre puntos, mediante una transformación en una dimensión m dada, para diferentes dimensiones. Para cada una de las dimensiones de transformación m se elige un épsilon , con cuyos datos la correlación integral está definida por:
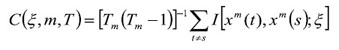
donde: Tm=T-m+1, t y s tienen rango de 1 a T-m+1 en la sumatoria y son restringidos tal que t≠s.
Los resultados de la aplicación de la prueba2 demuestran la existencia de patrones no lineales inmersos en el conjunto de datos, por lo cual se inicia el modelado mediante modelos no lineales ARMA - GARCH y luego mediante modelos de Redes Neuronales Artificiales.
Los modelos ARCH y GARCH, denominados así por su nombre en inglés, Generalizaed Autorregressive Conditionally Heteroscedastic, representan procesos con media condicional igual a cero. Sin embargo, también se puede considerar procesos dependientes de la media denominados ARMA-GARCH. En este tipo de modelos se puede considerar un modelo simple de regresión lineal con errores GARCH, que se expresa formalmente de la siguiente manera:
![]()
Un modelo ARMA con errores GARCH se expresa de la siguiente manera:
![]()
Finalmente, un proceso GARCH se define como:
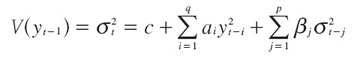
Los parámetros estimados para el modelo muestran que es significativa la dependencia sobre las varianzas rezagadas y que el modelo es diagnosticado de manera adecuada3.
Siguiendo con la metodología planteada, se procede al modelado mediante modelos de redes neuronales artificiales que conforman un componente del conjunto denominado sistemas expertos.
Basados en la eficiencia de los procesos llevados a cabo por el cerebro, e inspirados en su funcionamiento, varios investigadores han desarrollado desde hace más de 30 años la teoría de las Redes Neuronales Artificiales (RNA), las cuales emulan las redes neuronales biológicas, y que se han utilizado para aprender estrategias de solución basadas en ejemplos de comportamiento típico de patrones; estos sistemas no requieren que la tarea a ejecutar se programe, ellos generalizan y aprenden de la experiencia.
Las redes neuronales artificiales son modelos matemáticos no lineales inspirados por el sistema nervioso biológico, que simulan el proceso de aprendizaje del ser humano. Se utilizan principalmente para la clasificación y predicción de datos y variables. En lo que respecta a su uso en predicción, a diferencia de los modelos clásicos de regresión, la magnitud de los coeficientes para cada nodo o neurona no son importantes, esto porque no se puede esperar coherencia en sus signos; lo importante es el ajuste del modelo. Estos pesos, que expresan finalmente el conocimiento y capacidad de inferencia, deben estimarse mediante algún método de optimización no lineal. Éste finalmente definirá el tipo de aprendizaje que se desea utilizar.
El modelamiento de la neurona biológica es relativamente sencillo. Se compone de una entrada p, un valor de peso w, un bias b (este valor tiene como justificación que permite que la neurona artificial mueva su frontera de decisión, que es una recta, de tal forma que no pase por el origen), una función de suma Σ, una función de activación f y una salida a:
El Gráfico 5 muestra la representación de una neurona artificial; muchas de estas neuronas interconectadas forman una red neuronal. Se aprecia que la única entrada del exterior es p, el cual se multiplica con un valor específico de cada neurona w (peso); éstos son llevados a una sumatoria con otro valor propio de la neurona, denominado b. El valor resultante se lleva a través de f (función de activación o de transferencia), de donde sale el valor resultante, que es transmitido a la siguiente neurona o al exterior.
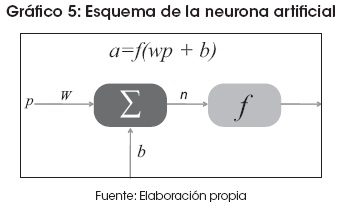
De acuerdo al número y a la distribución de las neuronas artificiales, ellas conforman capas o niveles. Capa o nivel es el conjunto de neuronas cuyas entradas provienen de la misma fuente (que puede ser otra capa de neuronas) y cuyas salidas se dirigen al mismo destino (que puede ser otra capa de neuronas).
Una red neuronal artificial es la interconexión de varias neuronas. El Gráfico 6 muestra una red neuronal estructurada en capas; es una de las estructuras en las cuales se pueden asociar las neuronas. En este sentido, los parámetros fundamentales de la red son: el número de capas, el número de neuronas por capa y el tipo y número de conexiones entre neuronas. No existe un método o regla que determine el número óptimo de neuronas ocultas para resolver un problema dado, generalmente se determinan por prueba y error, es decir, partiendo de una arquitectura ya entrenada, se realizan cambios aumentando y disminuyendo el número de neuronas ocultas y el número de capas, hasta conseguir la arquitectura que se ajuste a la solución del problema.
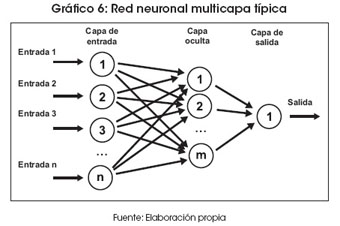
Luego de conformar el esquema de la red neuronal, se procede a la etapa de aprendizaje de la red. El aprendizaje es el proceso por el cual una red neuronal modifica sus pesos en respuesta a una información de entrada. Los cambios que se producen durante el proceso de aprendizaje se reducen a la destrucción, modificación y creación de conexiones entre las neuronas. En el caso de las redes neuronales artificiales, se puede considerar que el conocimiento se encuentra representado en los pesos de las conexiones. En realidad puede decirse que se aprende modificando los valores de los pesos de la red. Durante el proceso de aprendizaje, los pesos de las conexiones de la red sufren modificaciones, por tanto, se puede afirmar que este proceso ha terminado (la red ha aprendido) cuando los valores de los pesos permanecen estables. En forma general, se consideran dos tipos de aprendizaje: supervisado y no supervisado. La diferencia fundamental entre ambos tipos estriba en la existencia, o no, de un agente externo (supervisor) que controle el proceso de aprendizaje de la red.
Por lo general las redes neuronales aprenden por medio de ejemplos, los cuales comúnmente se presentan a la red en patrones de entrada y salida. El objetivo del aprendizaje o entrenamiento de la red es ajustar los parámetros de la red, pesos y umbrales, con el fin de que las entradas presentadas produzcan las salidas deseadas, es decir con el fin de minimizar la función de error.
De manera formal, existen dos categorías de algoritmos de aprendizaje: el descenso por gradiente, y técnicas de entrenamiento de segundo orden (gradiente conjugado, Levenberg-Marquardt -LM). Todos los algoritmos parten de una condición inicial xo y luego se modifican por etapas, de acuerdo con:
![]()
donde pk representa una dirección de búsqueda y el escalar positivo α es la tasa de aprendizaje que determina la longitud del paso. El entrenamiento finaliza cuando una de las siguientes condiciones se presenta:
- Cuando se ha alcanzado la cantidad máxima de iteraciones.
- Cuando se ha alcanzado el error final deseado.
- Cuando la ejecución del gradiente alcanza un valor por debajo del mínimo gradiente.
Las RNA se han empleado para resolver numerosos problemas, entre ellos, los económicos y financieros, destacando en gran medida su aplicación en la predicción de series temporales y su capacidad para detectar y explotar la no-linealidad existente en los datos, aun en condiciones en las existen datos incompletos o la presencia de ruido. También se destacan por su desempeño en la solución de problemas complejos, en los cuales el reconocimiento de modelos o comportamientos es importante. Su uso resulta especialmente útil en la modelización de aquellos fenómenos complejos en los cuales la presencia de relaciones no lineales entre las variables es habitual. La aplicación de este tipo de técnicas en el terreno de la economía ha proporcionado interesantes resultados, sobre todo en los campos de la teoría económica y la econometría. El gran aporte de esta metodología consiste precisamente en la eliminación de la hipótesis reduccionista de linealidad, que ha venido dominando el análisis económico a lo largo de su historia. Si bien dicha hipótesis simplificadora ha permitido formular modelos matemáticos con los que explicar el fenómeno económico, al no contemplar la no linealidad inherente a los sistemas económicos, dichos modelos ofrecían una visión parcial de la realidad. Desde el punto de vista de la econometría, principal herramienta de análisis y validación con la que cuenta el economista, no podemos olvidar que una de las hipótesis fundamentales sobre las que se construye el ya clásico Modelo Lineal Básico es, como su propio nombre indica, la linealidad de las ecuaciones. El empleo de técnicas econométricas sustentadas en una falsa linealidad ha conducido a la especificación de modelos incompletos, los cuales mostraban sus carencias al enfrentarse a fenómenos de dinámica no lineal.
El tipo de red neuronal utilizado en el presente trabajo es el Perceptrón Multicapa; cabe aclarar que no se utiliza la red neuronal de base radial por motivos de capacidad de inferencia y ajuste del mismo.
Se muestra a continuación el proceso de construcción de los modelos de redes neuronales, el cual consta de las siguientes etapas
- Normalización de datos
- Selección de variables de entrada.
- Estimación de los parámetros de los modelos
Las mencionadas etapas son exigidas por la metodología para un adecuado modelado y posterior pronóstico.
La sección que se describe a continuación debería ubicarse después del pronóstico, pero por razones de metodología se antepone a la del pronóstico, para mostrar los parámetros estimados. Esta estimación es resultado de un proceso de búsqueda del mínimo. Este mínimo resulta de la adecuada combinación de diferentes parámetros, proceso computacionalmente muy costoso pero en cuya búsqueda se pueden utilizar algoritmos genéticos. Este proceso se puede observar en el Gráfico 7, en el cual se trata de lograr convergencia mediante la minimización tanto de errores de entrenamiento como de validación.
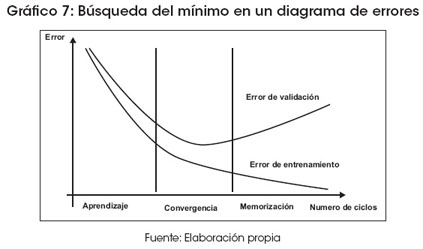
Los parámetros seleccionados se muestran en el Cuadro 1. En el Gráfico 8 se muestra la estructura utilizada para el modelo de pronóstico de demanda de potencial eléctrico.
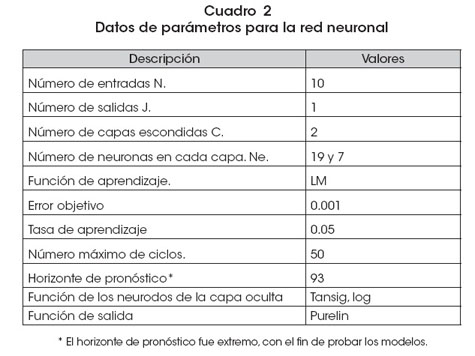
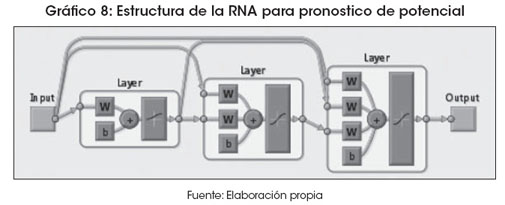
El último paso es poner la red neuronal optimizada en producción. Esto depende en gran medida del software que se esté utilizando y el entorno en que se encuentran los datos. En el presente estudio se utilizó la herramienta de MatLab referente a redes neuronales.
El Gráfico 9 muestra el ajuste logrado por la red neuronal artificial en las fases de entrenamiento (0.996), validación (0.995) y prueba (0.994).
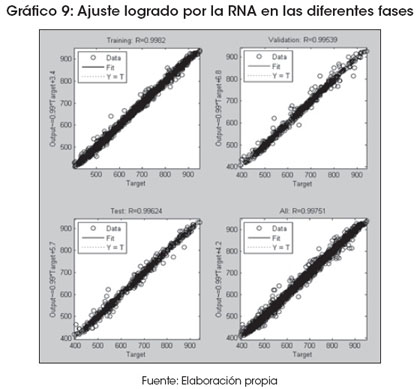
El pronóstico generado por la red neuronal para estimar datos futuros se muestra en el Gráfico 8, donde se puede apreciar que el pronóstico realizado es muy próximo a los datos reales. Esto se puede afirmar mediante los indicadores de MAE de 6 y MAPE de 0.00964.
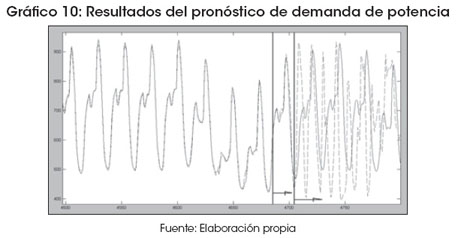
Se debe mencionar que la generalización de la red está influenciada por tres factores: el tamaño y eficiencia del conjunto de aprendizaje, la arquitectura de la red y la complejidad del proceso evolutivo del fenómeno, en este caso la demanda de potencia. Utilizar un conjunto de aprendizaje pequeño no resulta, necesariamente, en una mejor capacidad de predicción, pues este sobreaprendizaje hace que la red memorice detalles de la serie de tiempo, en vez de aprender la relación esencial entre los datos de entrada y salida. Para asegurar la apropiada generalización de la red, el modelo matemático debe ser validado bajo condiciones extremas. Esto se logra con un conjunto de datos que no hayan sido utilizados para el aprendizaje y son utilizados para la evaluación del modelo. Con estas recomendaciones se finaliza el análisis y modelado de la presente investigación.
5. Conclusiones
En el presente trabajo se estimaron básicamente cuatro modelos, los mismos que no son mutuamente excluyentes sino, más bien, complementarios. Esta afirmación se la realiza porque cada modelo captura ciertas características de la serie en estudio. Empero, la que mejores resultados muestra, dadas las características descritas de la serie, es el modelo matemático obtenido del entrenamiento una red neuronal artificial. Este modelo tiene un ajuste del 99 por ciento y un MAE y MAPE menores a los otros modelos.
Desde la perspectiva económica, se concluye que cualquier mejora en la disminución del error de pronóstico representa una mejora en el excedente del consumidor. El beneficio económico por la implementación de los modelos de redes neuronales artificiales en la predicción de la demanda de potencia eléctrica se presenta por la reducción de los costos incrementales generados por el error de pronóstico. Dichos costos adicionales se pueden producir en un primer escenario porque el pronóstico de la demanda de potencia sea superior al valor real, entonces el precio de generación de la potencia demandada es alto porque éste se halla con base en el costo de la última unidad generada para compensar el pronóstico de la demanda. El segundo escenario en el cual el pronóstico de la demanda es menor o inferior a la demanda real implica la disminución en la calidad de prestación del servicio en un mercado regulado por un sistema de calidad-penalidad.
El despacho y la operación en tiempo real están concebidos con el objetivo de reducir el exceso o déficit de carga que ocurrirían por el error del pronóstico. Cuando, durante el transcurso del día, se observa que el pronóstico de la demanda de potencia para la hora h con la cual se programó el despacho económico puede ser significativamente más alto que la demanda real en la hora h, mediante la actividad del despacho se permite que las empresas distribuidoras adviertan al CNDC esta situación, y se altere la programación inicial de despacho de carga. Mediante la operación en tiempo real se optimiza la actividad operativa, de tal manera que la generación total de carga compense la demanda real. Si se aprecian caídas en las tensiones locales porque el despacho de carga es inferior a la demanda real, el CNDC debe coordinar las actividades para que se aumente la producción de los generadores y se pueda despachar el déficit de carga. De esta forma se minimizan las pérdidas en cuanto a que la cantidad de potencia comprada corresponda a la que realmente se consume.
Con respecto al precio, con base en lo anterior, se puede mencionar que, a mayor exactitud y precisión en los pronósticos, las empresas no se ven perjudicadas por la disminución del costo unitario reflejada en la tarifa, porque sus ingresos representados dentro del costo unitario por distribución y comercialización siguen siendo los mismos. Sin embargo, como comercializadora puede obtener una mejora en el bienestar, porque al disminuir el costo unitario por prestación de servicio se supone un aumento en el consumo.
Artículo recibido en: agosto de 2010
Manejado por: ABCE
Aceptado en: marzo de 2011
Referencias
- García, A. (2010). Introducción a la regresión armónica dinámica. Análisis y predicción de la coyuntura económica. Universidad Complutense de Madrid. [ Links ]
- García, D. y A. Cabrera (2003). Predicción de la demanda eléctrica de corto plazo mediante redes neuronales artificiales. SIE. Centro Universitario de Ciencias Exactas e Ingeniería. Universidad de Guadalajara, México. [ Links ]
- Gobierno de Bolivia. (1994). Ley de electricidad N° 1604 de 21 de diciembre de 1994 . Reglamentos aprobados por D.S. N° 24043 de 28 de junio de 1995. [ Links ]
- Gonzales, V. (2007). “Un modelo Spline para pronóstico de la demanda de energía eléctrica”. Escuela de Ingeniería Industrial y Estadística, Facultad de Ingenierías, Universidad del Valle, Cali, Colombia
- Mallo, C. (2007). “Predicción de la demanda eléctrica horaria mediante redes neuronales artificiales”. Departamento de Economía Cuantitativa. Universidad de Oviedo.
- Martinic, N. Gamma. (2008). “Ray Astrophysics, Chacaltaya Cosmic Rays Observatory”. Universidad Mayor de San Andrés, La Paz, Bolivia.
- Mendoza, J. (2006). “Pronóstico de carga a corto plazo utilizando redes neuronales artificiales”. Scientia et Technica, Universidad Tecnológica de Pereira - Colombia
- Pérez, S. y F. Garbati. (2008). Modelo matemático para la demanda de potencia. Universidad Nacional de Colombia. Red de Revistas Científicas de América Latina, El Caribe, España y Portugal. Redalyc. [ Links ]
- Mallo, C. (2008). “Predicción de la demanda eléctrica horaria mediante redes neuronales artificiales”. Departamento de Economía Cuantitativa. Universidad de Oviedo.
- Sante, R. (2009). “Transformada rápida de Fourier”. Departamento de Economía Cuantitativa. Universidad Complutense de Madrid
- Tabares, H. y J. Hernández (2008). “Mapeo de curvas típicas demanda de energía eléctrica del sector residencial, comercial e industrial de la ciudad de Medellín, usando redes neuronales artificiales y algoritmos de interpolación”. Departamento de Ingeniería Eléctrica, Facultad de Ingeniería, Universidad de Antioquia.
- Villada, F., D.R. Cadavid y J.D. Molina (2008) .“Pronóstico del precio de la energía eléctrica usando redes neuronales artificiales”. Grupo de manejo eficiente de la energía (GIMEL), Universidad de Antioquia, A.A. 1226, Medellín, Colombia. Redalyc.
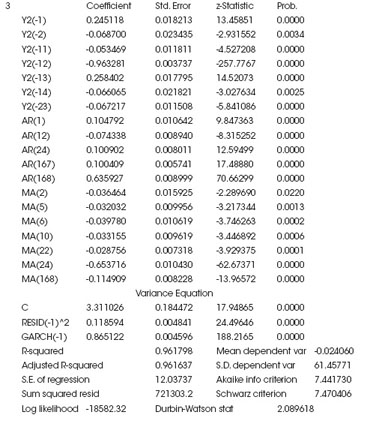

Anexo 1: Simulación de series autorregresivas integradas con medias móviles de orden superior
Cada serie autoregresiva de primer orden, denominada AR(1), se puede comenzar con un parámetro, que se denomina Ø1. La condición de serie autoregresiva estacionaria está dada por -1‹Ø1‹+1:
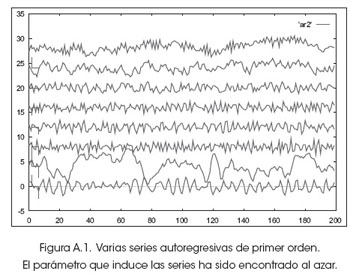
En la figura A.1 se muestran algunos fragmentos simulados de series ARIMA(p,d,q). Se ha utilizado ruido blanco para generar las series temporales. El σ de la serie aleatoria se ha tomado como 1.
Se puede observar que cuando las autocorrelaciones oscilan, entonces la serie temporal simulada tiende también oscilar con una frecuencia cercana a la frecuencia de Nyquist.
En la figura A.3 se puede ver la potencia espectral de las series temporales simuladas en la figura A.1. Nótese que las coordenadas están en escala log-log. El rango de las frecuencias en la figura A.3 corresponde al rango comprendido desde un valor cercano a cero hasta la frecuencia de Nyquist, esto es, 0.5 en escala del inverso de la escala del muestreo para las series temporales con un intervalo de muestreo dado.
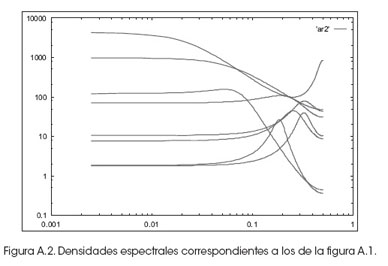
Como regla general, en la potencia espectral, ya sea que posea una función decreciente o no, cuando la serie temporal varía en forma suave o bien es una función creciente, la serie temporal oscila entre un valor y el siguiente.
En cuanto a las series autoregresivas de orden superior, es decir, cuando p>2, d>2, y q>2, que se muestran en la Figura A.3, los parámetros se encuentran dentro del triángulo de estacionariedad. Esas condiciones implican que los valores para los coeficientes ØØ se 1 y 2 encuentren al interior o sobre la frontera del triángulo de estacionariedad. A esto se suma que existen diferentes perfiles de las series temporales cuando los parámetros se encuentran en una de las cuatro zonas limitadas por la parábola -0.25 x Ø12 y la línea Ø1=0. En todos los casos se trata ya sea de comportamiento de exponenciales atenuados o bien de funciones sinusoidales atenuados. Es conveniente simular estas series temporales para estudiar la clasificación de estos perfiles. Desde el punto de vista algebraico, buscar estos comportamientos es equivalente a obtener raíces de un polinomio. Cuando dichas raíces son reales, entonces se trata de perfiles de exponenciales atenuados; caso contrario, cuando son complejos, entonces se trata de sinusoidales atenuados.
Finalmente, en la Figura A.4 se aprecian las potencias espectrales para cada una de las series autorregresivas integradas de medias móviles. Tanto en la figura A.2 como en la A.4, cada potencia espectral se multiplicó por 2n, donde n va desde 0 hasta 19, para evitar que las potencias espectrales se confundan entre sí. La obtención de la potencia espectral es a través de la convolución del ruido y el espectro del proceso lineal.
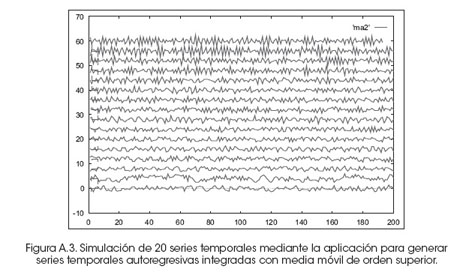

De las potencias espectrales obtenidas se puede mencionar que las series autoregresivas y de medias móviles integradas poseen un espectro relativamente constante, excepto cuando aparecen oscilaciones cerca de la frecuencia de Nyquist.
Para las series autoregresivas de medias móviles integradas de orden superior las Figuras A.1 y A.3 se muestran las series temporales generadas con los coeficientes que cumplen que: -1‹ z ‹+1 y i ‹|1|
Aquí vale la pena mencionar la manera teórica de obtener la potencia espectral de las series simuladas. Básicamente se remplaza en una función entera de operadores la expresión e h por cada operador, y se obtiene sacando módulos al cuadrado, funciones enteras en cos^2rnf h con n algún número entero. Por supuesto que se tiene otra manera de comprobar esto, y es obteniendo la transformada de Fourier digital de las series ARIMA(p, d, q) de entrada.
Anexo 2: Simulación con modelos armónicos
En los análisis modernos de la teoría de la información perteneciente a la ingeniería de sistemas, en el espacio de la frecuencia se utiliza la transformada de Fourier digital, haciendo uso del teorema del muestreo. Es decir, tratamos de muestrear la función cuya transformada deseamos conocer, de tal modo que el intervalo del muestreo L sea lo suficientemente pequeño como para que dos de esas muestras nos definan la longitud de onda de Nyquist. De esa manera esta última definirá la máxima frecuencia existente en la función buscada.
Si se desea encontrar en forma numérica las transformadas digitales, las ecuaciones:
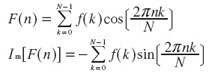
permiten estimar y mostrar los comportamientos a corto y largo plazo, mediante la función par e impar.
Lo anterior se puede expresar de mejor manera para su aplicación como:
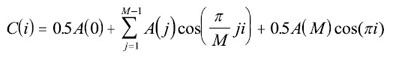
El problema central de la simulación correspondiente a la presente sección corresponde a generar series artificiales con base en un modelo cuyos parámetros fueron estimados previamente. Para lograr este objetivo se utiliza el siguiente modelo, que escrito de manera general se denota como:

En la anterior ecuación se expresan las combinaciones complejas que muestran las periodicidades de un periodo real contenido en una serie temporal. De este modo se ajusta a un modelo matemático. Esto es importante, sobre todo para generar series temporales mediante la simulación.
Para el análisis de las series temporales, por ejemplo correspondientes a la variabilidad climática, cada uno de los factores climáticos día a día se somete al análisis armónico, pues para que la transformada de Fourier detecte la frecuencia se requieren muchos más ciclos en la serie temporal. Para este fin se simula el comportamiento con la primera, segunda y cuarta armónica; de esta manera de obtiene un comportamiento representativo de los factores climáticos y se conoce si estas series son o no estacionales.
En la Figura A.5 se muestra la simulación, con las correspondientes armónicas que la posibilitaron, y los correspondientes parámetros del modelo matemático de comportamiento expresado en el primer modelo matemático.
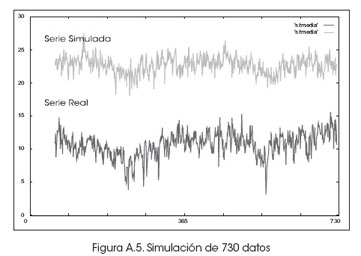
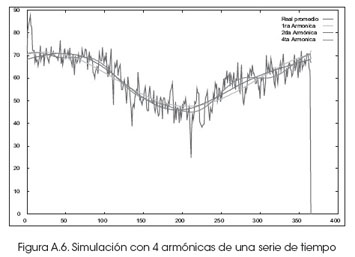
Anexo 3: Simulación con modelos ARMA-GARCH
La finalidad de un modelo no es, naturalmente, reproducir la realidad en toda su complejidad, sino captar formalmente lo que es esencial para comprender algún aspecto de su estructura o comportamiento.
En el presente caso se simulan series que corresponden a los modelos ARMA-GARCH. La simulación que se realiza muestra datos que poseen las mismas características matemáticas, estadísticas y físicas que la serie original o real que se modela. Estas series deben aproximarse tanto como sea posible a la serie inicial. La aplicabilidad de estas series artificiales se muestra en la creación de datos para analizar diferentes escenarios, y para completar series de datos incompletas y otros que puedan presentarse.
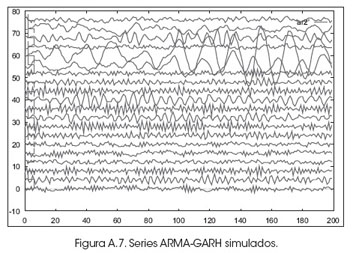
En la Figura A.7 se muestran series ARMA-GARCH simuladas. En tales gráficos se podrán observar la serie original en la parte inferior y las series simuladas en las series que se grafican en la parte superior.
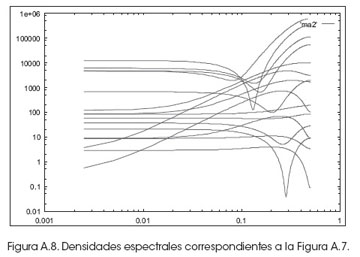
En la Figura A.8 se muestra el espectro de las series simuladas, las mismas que muestran que superan la frecuencia de Nyquist.
Anexo 4: Aspectos importantes de las redes neuronales artificiales
Estructura y aprendizaje de la red de propagación hacia atrás
En la red de la Figura A.9 se muestra una capa de entrada con n neuronas y una capa de salida con m neuronas y al menos una capa oculta de neuronas internas. Cada neurona de una capa recibe entradas de todas las neuronas de la capa anterior y envía su salida a todas las neuronas de la capa posterior. No hay conexiones hacia atrás, denominadas feedback, ni laterales entre neuronas de la misma capa.
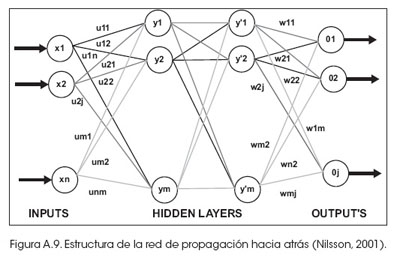
La aplicación de la red tiene dos fases, una hacia delante –feedforward- y otra hacia atrás – backpropagation. Durante la primera fase el patrón de entrada es presentado a la red y propagado hacia delante a través de las capas, hasta llegar a una capa de salida. Obtenidos los valores de salida de la red, se inicia la segunda fase, comparándose estos valores con la salida esperada para obtener el error. Se ajustan los pesos de la última capa proporcionalmente al error. Se pasa a la capa anterior con una retropropagación del error, ajustando convenientemente los pesos y continuando con este proceso hasta llegar a la primera capa. De esta manera se han modificado los pesos de las conexiones de la red para cada ejemplo o patrón de aprendizaje del problema del que conocíamos su valor de entrada y la salida deseada que debería generar la red ante dicho patrón.
A diferencia de la red perceptron multicapa, la técnica de propagación hacia atrás o generalización de la regla delta requiere el uso de neuronas cuya función de activación sea continua, y, por tanto, diferenciable. Esta característica es la que obviamente la distingue en general.
Describiendo la red de propagación hacia atrás, ésta se inicia con la presentación de un patrón de entrada, X : x, x, …, x, y especificación de la salida deseada que debe generar la red: d1, d2, …, dM. Luego se calcula la salida actual de la red, para lo cual se presentan las entradas a la red y se calcula la salida que presenta cada capa hasta llegar a la capa de salida de la red y1, y2, …,yM. Esto último implica aplicar los siguientes pasos:
- - Se calculan las entradas netas para las neuronas ocultas procedentes de las neuronas de entrada. Para una neurona oculta j:
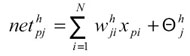
- en donde h se refiere a magnitudes de la capa oculta; el subíndice p, al p-ésimo vector de entrenamiento, y j a la j-ésima neurona oculta. El término Θ puede ser opcional, pues actúa como una entrada más.
- - Se calculan las salidas de las neuronas ocultas:
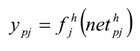
- - Se realizan los mismos cálculos para obtener las salidas de las neuronas de salida (output).
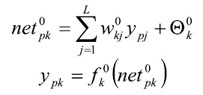
Luego de cumplir estos pasos, se calculan los términos de error para todas las neuronas. Si la neurona k es una neurona de la capa de salida, el valor de delta es:
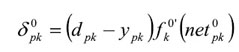
La función f, como se citó anteriormente, debe cumplir el requisito de ser derivable, lo que implica la imposibilidad de utilizar una función escalón. A continuación se muestra la salida sigmoidal:
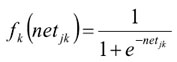
La derivada de la función f sigmoidal es:
![]()
por lo que, en términos de error, la neurona de salida es:
![]()
Si la neurona j no es de salida, entonces la derivada parcial del error no puede ser evaluada directamente; por lo tanto, se obtiene el desarrollo a partir de valores que son conocidos y otros que pueden ser evaluados.
La expresión obtenida en este caso es:
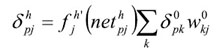
donde observamos que el error en las capas ocultas depende de todos los términos de error de la capa de salida. De aquí surge el término propagación hacia atrás. En particular, la función sigmoidal:
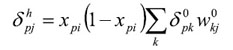
donde k se refiere a todas las neuronas de la capa superior a la de la neurona j. Así, el error que se produce en una neurona oculta es proporcional a la suma de los errores conocidos que se producen en las neuronas a las que está conectada la salida de ésta, multiplicado cada uno de ellos por el peso de la conexión. Los umbrales internos de la neurona se adaptan de forma similar, considerando que están conectados con los pesos desde entradas auxiliares de valor constante.














