Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Latinoamericana de Desarrollo Económico
versión impresa ISSN 2074-4706versión On-line ISSN 2309-9038
rlde n.13 La Paz jun. 2010
ARTICULO ORIGINAL
Las empresas en Santa Cruz, ¿continúan en una estructura monocéntrica?
Xavier Salazar y Miguel Atienza
Resumen
Este trabajo contrasta la hipótesis de que, en la ciudad de Santa Cruz de la Sierra (Bolivia), las empresas continúan concentradas de forma monocéntrica. Para ello se estima un modelo estadístico que compara densidades locales para contrastar la hipótesis monocéntrica. Los índices de concentración y diversificación de actividades encontrados basados en datos empíricos de 2007, dan la pauta de patrones de concentración relevantes según anillos y posibles subcentros.
Abstract
This paper contrasts the hypothesis that, in the city of Santa Cruz de la Sierra (Bolivia), companies/enterprises are still concentrated in a monocentrical way. To proof this hypothesis, a statistical model is estimated to compare local densities. Indices concerning concentration and activities diversification, based on empiric data from 2007, give the hint of relevant concentration patterns according to rings and possible sub – centers.
Keywords: Monocentrical Enterprise Concentration, Comparative Statistical Model,
JEL Classification: L00; L1; C1; C4;D2; D24
Introducción
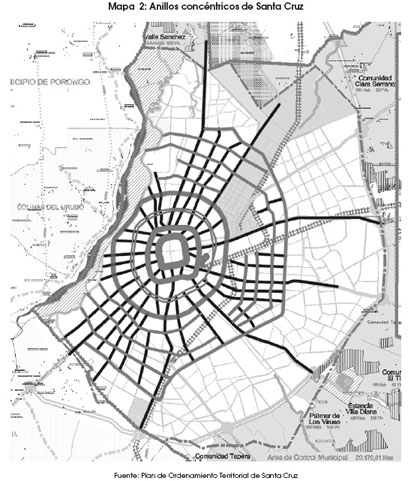
Este trabajo se enfoca en la organización intra-urbana de la ciudad de Santa Cruz, ordenada y planificada al mejor estilo del modelo de Alonso, con una estructura que pasó de reticular, en la Colonia, a un claro monocentrismo, en los siglos XIX y XX; donde la estructura caminera rodea el Distrito Central de Negocios (DCN) con anillos radiales concéntricos. En estos momentos, tras 30 años de crecimiento poblacional y constante migración campo-ciudad sobre el promedio departamental, la ciudad pudo haber pasado a una estructura policéntrica.
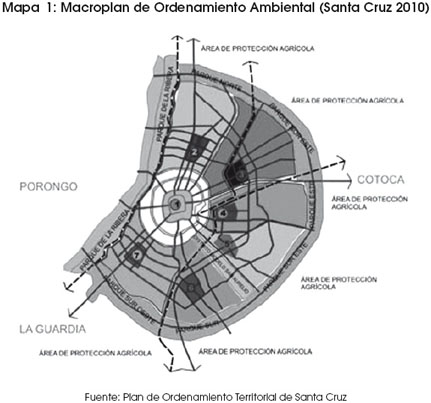
El análisis de la estructura de la ciudad es de interés no sólo como un espacio geográfico donde se pueden formular políticas, sino también porque conforma un medio ambiente para facilitar las relaciones socioeconómicas que se desarrollan dentro de sus límites. El planificar y generar nuevos subcentros dentro de una ciudad debe velar tanto por dotar de bienes y servicios públicos suficientes para la población como también de un espacio adecuado a las empresas que dan empleo a sus habitantes. El Plan de Ordenamiento Territorial (PLOT) de Santa Cruz, la herramienta para el manejo del territorio en sus variables físico espaciales del Plan Estratégico de Desarrollo Municipal (PEDM), propone seis nuevos subcentros enfocados más desde el punto de vista urbano residencial que desde el empresarial (véase mapa 1). Es, sin embargo, necesario evaluar las nuevas centralidades propuestas en el macroplan de ordenamiento ambiental desde el punto de vista empresarial, para lograr tanto la provisión adecuada de amenidades residenciales como para potenciar las ventajas de la proximidad con las empresas.
El carácter monocéntrico o policéntrico de una ciudad no sólo se basa en dónde las personas viven, sino también en dónde se desarrollan las actividades productivas que las personas hacen para vivir. Para ello se necesita identificar los patrones de localización de las actividades empresariales de la ciudad de Santa Cruz; y según la concentración y especialización de sus actividades poder justificar la necesidad de nuevos subcentros.
Es verdad que algunos sectores empresariales “siguen” a los conglomerados de personas, por cuanto se sitúan en zonas de alta densidad poblacional, ya que esto les representa un mayor mercado. Sin embargo, las amenidades que atraen a las personas no son las mismas que atraen a las empresas; al entender esto se puede tener una mejor evaluación sobre si los subcentros propuestos son idóneos para enmarcar y focalizar futuras políticas de mitigación ambiental, ventajas fiscales y otras políticas de apoyo a la consolidación de un nuevo subcentro.
Enfocando la atención en la localización de las empresas que participan en la economía de Santa Cruz de la Sierra, antes que en la población residente, se pueden responder más a cabalidad las siguientes preguntas:
¿Cuál es la distribución espacial de las empresas en relación a la estructura productiva de Santa Cruz? Giuliano y Small (1991) y McMillen y McDonald (1998) encontraron que diferentes centros tienen caracteristicas de mix industrial muy diferentes. Algunos subcentros son muy especializados y otros, imitando al centro histórico, tienen una composición diversificada1. Es importante estudiar lo diversificado que es cada subcentro, para saber si se requieren políticas que apoyen la tendencia hacia la diversificación de actividades o lograr una distribución espacial policéntrica más especializada que incentive las economías internas y externas de escala de forma natural. Para ello se estimarán los índices de concentración y dispersión de las actividades cruceñas según anillos o zonas propuestas para subcentros. Al calcular los índices de concentración y dispersión se lograrán dos cosas; por un lado, un punto inicial para que, en investigaciones futuras sobre el mismo tema, se pueda medir el impacto de políticas del gobierno central o regional sobre el tejido empresarial de Santa Cruz, y, por otro, se cuente con estadísticos instrumentales para evaluar la hipótesis central de este trabajo. Asimismo se calcularán índices de diversificación o especialización mediante los índices de Entropía Total, Relacionada y no Relacionada, que permiten hacer un ranking de zonas o anillos según su especialización, útil para nuevos emprendimientos.
¿La localización de las actividades económicas, en la ciudad de Santa Cruz de la Sierra, se concentra espacialmente en anillos concéntricos según el planteamiento teórico mono céntrico de un Distrito Central de Negocios2 (DCN)? Esta pregunta tiene relevancia actual, por cuanto existen nuevas competencias autonómicas3 que proporcionan instrumentos de política municipal que pueden ser aprovechados para incentivar la localización y agrupación de algún sector o tipo de actividad particular, hacia alguna zona específica4 dentro de la ciudad para lograr mayor impacto en el desarrollo o la contención ambiental. Para evaluar si Santa Cruz ya se puede considerar una ciudad policéntrica o continúa siendo una ciudad monocéntrica, se empleará el modelo de Odland (1978) que permite abordar el problema desde un punto de vista estático comparativo.
Dado el acelerado crecimiento poblacional de Santa Cruz5 de los últimos años debido a masivas migraciones campo-ciudad, y evidenciando que, según los índices de especialización estimados por la Cámara de Industria y Comercio (CAINCO), algunos subcentros propuestos en Santa Cruz puede que tengan una fuerte especialización agroindustrial que potencian las fuerzas dispersoras del DCN, se plantea como hipótesis del trabajo que la estructura empresarial de Santa Cruz de la Sierra ya se comporta como una ciudad policéntrica.
1. Revisión bibliográfica
La localización de una empresa es clave para diversos factores que influyen en su competitividad, como el acceso a mercados, la accesibilidad a recursos y posibles acuerdos entre empresas del mismo o diferente sector en que se desarrolle su actividad. Se considera que quien comenzó a formalizar la teoría de localización de las actividades empresariales fue Johann H. Von Thunen (1826), basado en el principio de la función de puja por productividad–distancia de David Ricardo, para estudiar el mercado de la tierra urbana y agrícola mediante funciones de puja que varían con la distancia. Posteriormente los estadounidenses Ricard M. Hurd (1903) y Robert M. Haig (1926) se dedicaron al problema de la renta de la tierra y el ingreso, y en particular a explicar el resultado contraintuitivo que existía en las ciudades americanas, donde los pobres vivían cerca del centro, donde la tierra era cara, y los ricos vivían en la periferia, donde la tierra era barata.
William Alonso (1960) y Muth (1969) dieron un paso más allá para explicar la distribución espacial de los precios de las casas, consumo de tierra y orden espacial de los residentes determinados por los costos de transporte al centro de una ciudad monocéntrica, naciendo el concepto de Distrito Central de Negocios6. Para ello establecieron dos hipótesis:
a) El precio de la tierra decrece con la distancia al DCN (Pendiente negativa del gradiente de renta)
b) El consumo de la tierra per cápita, se incrementa con la distancia al DCN (pendiente negativa del gradiente de densidad)
Según Pérez y Polèse (1996), el DCN puede presentar distintas formas; aquí se mencionan tres, pudiendo cada una de ellas evolucionar como modelo propio o como combinación entre ellas:
1. Modelo de consolidación del DCN en el centro histórico: En este modelo, el DCN se consolida en lo que es el centro histórico; entonces el DCN se renueva en el centro histórico;
2. Modelo de desplazamiento del DCN de lo que es el centro histórico: aquí el DCN no es el mismo que el centro histórico, es decir que, dada la evolución en la estructura económica de la ciudad, el DCN aparece en una localización diferente a la del centro histórico. La concentración busca otra localización hasta conformarse en un área diferente a la original (Lungo, 1998);
3. Modelo polinuclear del DCN: dada la evolución de la ciudad hacia un modelo polinuclear, no existe un DCN dominante, porque hay diversos centros diferenciados (pero ninguno es lo bastante grande para ser llamado centro) (Krugman, 1996).
Rosen (1974) y Coulson (1989) probaron el modelo monocéntrico en un marco hedónico, utilizando variables dummy de localización (Norte, Sur, Este y Oeste) para capturar subcentros que pueden tener gradientes propios que se fundirían con el gradiente del DCN. El Plan de Ordenamiento Territorial (PLOT) de Santa Cruz también hace referencia a distintas densidades poblacionales en diferentes zonas de la ciudad, lo que origina los subcentros propuestos por el macroplan de ordenamiento ambiental Santa Cruz 2010.
Richardson (1977) notó la existencia empírica de un gradiente de renta positiva que era contrario a las hipótesis de Alonso (1960), y especuló que era efecto de grandes barrios o urbanizaciones, aunque también existían las probables fuerzas dispersoras de las externalidades de congestión, errores de medición de la distancia y la diferencias medioambientales en el que el modelo se desarrolla. De esta forma dio paso a la búsqueda de condiciones formales para pasar de un modelo monocéntrico a uno policéntrico. Anas (1998) indica que existen tres aproximaciones de modelos que ponen a prueba la monocentralidad:
1. Point Pattern Analysis: Desarrollado por Thomas (1981), define estadísticos de distancia entre unidades y las compara con distribuciones teóricas tales como la postulada por Christaller (1966) o por una distribución lograda al azar por un proceso Poisson. Una aplicación empírica de este análisis la hizo Getis (1983) para la ciudad de Chicago.
2. Análisis de fractales.7: Desarrollado por Batty y Longley (1994) para un estudio de fronteras en Gales. Los fractales de dimensión permiten representar patrones de desarrollo bidimensionales, capturando irregularidades tanto en el interior como en el exterior de un área. Es un método utilizado para analizar la frontera de una ciudad, porque el fractal se mantiene ante cambios de escala.
3. Estructura urbana por comparación de densidades: Una visión intuitiva y simplificadora, utilizada por McDonald (1987) para el mercado laboral, es identificar uno o más centros de empleo y estimar cómo dichos centros afectan el empleo y la densidad de población alrededor de ellos. Giuliano y Small (1991) definen el centro (conteniendo el DCN) como un subcentro tal como un agrupamiento de zonas continuas, todas con una densidad de empleo que excede un mínimo D, y que de manera conjunta exceden un mínimo E. Estas definiciones facilitan la comparación entre centros dentro de una ciudad, ya que el patrón de centros puede ser sensible a los valores de corte D y E y a la escala.
Esta investigación se enmarca dentro de la perspectiva de desarrollo empresarial, para el análisis de subcentros por comparación de densidades. La investigación no tiene el objetivo de proponer nuevos subcentros, sino evaluar aquellos que se plantearon en el macroplan de ordenamiento ambiental. Teniendo en cuenta que los subcentros no eliminan la importancia del DCN (Mc Donald y Prather, 1994), el interés de conocer si una Santa Cruz policéntrica mediante condiciones formales se debe a que algunos subcentros menos especializados tienen la potencialidad de convertirse en otras ciudades (como sucedió con la ciudad de El Alto, en La Paz) y otros subcentros tienden a convertirse en zonas especializadas en algún sector, y es esta potencialidad la que permite a las empresas ser más competitivas y generar avances tecnológicos. Este trabajo busca distinguir cuáles de los centros propuestos tienen potencialidad hacia la especialización, para enfocar las políticas municipales que los potencien, y así acelerar el desarrollo productivo.
Para ello se utiliza el modelo de Odland (1978), que, dentro de la aproximación por comparación de densidades, determina el número, tamaño y localización de los subcentros simultáneamente con la distribución de la población. En dicho modelo se considera que el ordenamiento de las actividades productivas es el resultado del balance entre las condiciones de consumo de tierras productivas y las condiciones de consumo de tierra residencial.
Las condiciones de consumo de tierras productivas residenciales sustituidas por actividades empresariales en una o varias zonas conducen a ventajas de economías de escala o economías de aglomeración, que son dadas en concentraciones de actividades del mismo sector y/o de sectores complementarios. Las condiciones para las actividades residenciales son establecidas funcionalmente por personas que trabajan y sus costos de transporte son inherentes a su actividad. De esta forma se logra el balance entre las condiciones de producción (como proximidad a su centro de trabajo) y las condiciones de uso residencial (proximidad a su domicilio).
Estas consideraciones son formalizadas en un modelo matemático de programación que localiza las actividades productivas y la población sobre un conjunto finito de zonas y determina el número de viajes al trabajo entre cada par de zonas según la densidad de población, el costo de transporte y la especificación de las condiciones de producción y consumo residencial. El proceso de modelación plantea un conjunto de condiciones formales que son asociadas con soluciones de densidad poblacional y distancia entre zonas. Estas condiciones son comparables con las soluciones de densidad poblacional y distancia entre zonas y el DCN de una ciudad monocéntrica, y ésta es la base para las pruebas estadísticas de la hipótesis de monocentralidad aplicable a una ciudad en particular.
El test es básicamente una comparación de densidades por zonas y puede ser planteado teóricamente de la siguiente manera: si la sumatoria de los costos marginales de producción, transporte y congestión residencial (residential crowding) es pequeña en relación con la densidad de población (primera condición) y el área de extensión de la ciudad (segunda condición), la estructura monocéntrica deja de mantenerse.
Este tipo de test de monocentralidad se enmarca en la aproximación por comparación de densidades utilizada por primera vez por McDonald (1987) para el mercado laboral. Esta aproximación es más simple que aproximaciones como el Análisis de Patrón de Puntos8, utilizada por Thomas (1981), o el análisis de fractales desarrollada por Batty y Langley (1994), porque existe discrecionalidad al definir los subcentros. Teniendo esto en cuenta, el modelo se especifica teóricamente bajo el supuesto de que la ciudad puede ser tratada como un número finito de zonas iguales que no se intersectan entre sí.
2. Especificación del modelo de Odland
Sea Qj el nivel de producción de la zona j, y sea f(Qj) el costo de producción por unidad 9 de la zona j . Sea Pi la población en la zona i, y sea g(Pi) la pérdida de ingreso real per cápita10 en la zona i, donde dicha pérdida es medida como el ingreso necesario para restaurar los niveles de utilidad en la zona de menor densidad. Las funciones f(Qi) y g(Pi) pueden variar de zona a zona por las amenidades locales derivadas del medio ambiente.
Entre cada par de zonas se logra un patrón que minimiza la suma de costos de producción, costos de transporte de los conmutantes entre cada par de zonas y las pérdidas de ingreso de la población. Esto corresponde formalmente a la minimización de la función objetivo:
![]()
Donde tij es el costo de conmutación entre la zona i y la zona j, y Nij es el número de conmutantes que viajan de la zona i a la zona j
Dicha minimización está sujeta a cuatro restricciones:

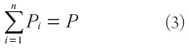
![]()
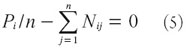
La primera dice que la producción total Q es suficiente para ocupar el total de la mano de obra de la ciudad, P es la población total de la ciudad, q es la producción por empleado, y n es el número de personas por trabajo. El modelo supone pleno empleo.
La segunda restricción asegura que cada miembro de la población de la ciudad tiene una residencia en alguna zona en particular. Se asume que cada individuo que trabaja es un dueño de hogar.
La tercera restricción asegura que cada zona reciba suficientes conmutantes para lograr la producción asignada a esa zona.
Finalmente, la última restricción logra que el número de conmutantes saliendo de cada zona no exceda el número de empleados residiendo en cada una de las zonas.
Al minimizar el Lagrangiano se pueden obtener las condiciones Kuhn Tucker, cuyo procedimiento se detalla en el Anexo 7.2, y cuyo principal resultado es la condición:
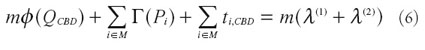
Si esta condición se mantiene, estaríamos en una ciudad monocéntrica; si la ciudad es policéntrica, la igualdad se rompería y se convertiría en mayor.
Los precios sombra representados por λ(1) y λ(2) capturan la densidad de la población de la ciudad y la densidad del área de extensión de la ciudad, respectivamente.
Para realizar el test de monocentralidad, el procedimiento teórico empleado mide la relación entre pares de zonas, de forma que se pueda medir la relación de una zona con el centro. Para poder usar la información disponible, Odland utiliza distancias entre las zonas en lugar de costo de transporte y densidad poblacional en zonas de tamaño irregular, en lugar del número de residentes de zonas de igual tamaño. La relación entre costo de transporte y distribución poblacional se redefine como:
![]()
Donde Y es la función que describe el costo marginal de incrementar la densidad poblacional y tiene una forma logarítmica, y S es la distancia entre la zona i y el DCN. Luego se define la diferencial de densidades poblacionales como dij=Di-Dj
Para lograr la ecuación a estimar de la condición para ver si la ciudad es monocéntrica
![]()
Donde xij es una transformación de la fución de distancia Sij tal que:
Xij=Sij si Sij< r teniendo que r es el radio circular del DCN
Xij=2r-Sij si Sij> r
Entonces, si los parámetros de la ecuacion estimada tienden a C1=0, C2=1, C3=0, estaremos ante una forma monocéntrica, y si los parámetros satisfacen C1<1 y C2>0, estaremos ante una forma estructural policéntrica.
La condición Odland para la monocentralidad puede ser testeada econométricamente con un test de Wald, e inclusive tiene la flexibilidad de poder reemplazar la diferencia de densidades poblacionales por una diferencia de densidades empresariales medida por el índice de concentración empresarial. Y puesto que utiliza la distancia entre zonas como aproximación al costo de transporte, también existe la flexibilidad de utilizar contigüidad de zonas.
3. Metodología de investigación
La unidad de análisis son las empresas que desenvuelven sus actividades productivas en la ciudad de Santa Cruz de Sierra, en Bolivia, con el fin de analizar cómo se agrupan dentro de las unidades vecinales para conformar una estructura monocéntrica o policéntrica.
Para ello, utilizaremos información secundaria a manera de muestra de la población total de empresas que desarrollan sus actividades en Santa Cruz. En 2007, el Registro de Comercio estimó una población total de 7.915 empresas formales activas en Santa Cruz, de las cuales se trabajará con 2.221 empresas (de las 2.449 empresas registradas en la Cámara de Industria y Comercio, CAINCO, en dicho año).
El estudio se limita a 2.221 empresas porque varias de ellas no pudieron ser ubicadas mediante la dirección que pusieron en la base de datos CAINCO, bien porque no estaban claras, bien porque el portal www.santacruzvirtual.com no tenia registrada la calle. También había otras cuya dirección quedaba en una zona no urbana o bien en otro municipio. De las empresas que fueron ubicadas, 52 tuvieron que ser sometidas a uno de estos supuestos11:
1. En caso de haber calles del mismo nombre en distintos barrios, y que no se especificaba el barrio, se tomó el barrio más cercano al centro.
2. En caso de que la empresa estuviera en una avenida principal que divide dos unidades vecinales, se tomó la unidad vecinal más lejana al centro.
Se reclasificaron las empresas de CAINCO según el Código Industrial Internacional Único (CIIU) a uno, dos y tres dígitos.
Para estimar las distancias de cada unidad vecinal al centro urbano, se cruzó la información obtenida de tres fuentes primarias: estadísticas obtenidas del Instituto Nacional de Estadística (INE), el Plan de Ordenamiento Territorial (PLOT 2003 -2010), publicado por el Plan Regulador de Santa Cruz, y el Informe Distrital elaborado por el Centro de Estudios Empresariales de la CAINCO (CEBEC/CAINCO).
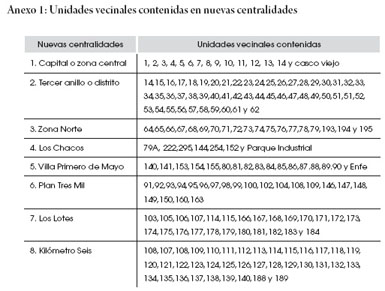
Se hace uso de una técnica descriptiva mediante índices de concentración y especialización según las zonas planteadas como subcentros por el PLOT. Los subcentros planteados por el Macro Plan de Ordenamiento Ambiental son 7, y fueron delimitados por criterios de densidad poblacional (véase Anexo 7.1):
También se realizó la comparación mediante anillos concéntricos, como lo sugiere el modelo de Alonso. Una vez estimado el modelo de Odland (1978), se verificó la monocentralidad mediante la prueba conjunta de coeficientes de Wald (véase mapa 2). Se emplearon los anillos detallados en el capítulo de morfología urbana del primer tomo del PLOT Santa Cruz 2010, y no así los propuestos por el nuevo plan de ordenamiento vehicular de la Alcaldía de Santa Cruz, que cuenta con más anillos, pero que aún no es oficial por estar siendo discutido con los transportistas en la actualidad. Estos nueve anillos concéntricos no acaparan la totalidad de la dimensión de la ciudad; es por ello que las empresas que están fuera del noveno anillo están catalogadas como “No ubicadas”.
La diferencia principal entre centralidades y anillos radicó en el costo de transporte reflejado en la distancia hacia el centro. Las centralidades asumieron una reducción de costos de transporte totales al evitar tener que trasladarse al centro para obtener algunos bienes que no logran en su mismo subcentro. En cambio, los anillos suponen que los agentes toman la decisión de manera individual respecto a la distancia entre su mercado objetivo y sus proveedores.
A fin de estimar la localización de las empresas, el índice de Ellison y Glaeser (1997) fue considerado el más apropiado como Índice de concentración empresarial, porque reúne características interesantes desde el punto de vista estadístico. Sin embargo, la incorporación del índice de Herfindhal restringe el uso de este índice, ya que no se cuenta con estadísticas de participación de mercado de las empresas. Ante esta restricción, se optó por utilizar el Cociente de Concentración Geográfica Primaria, definido como:

El rango de G oscila entre 0 y 1, pero si el numerador llega a ser menor puede llegar a tomar valores negativos. Para ver el desarrollo lógico de la expresión, supongamos una ciudad dividida en M subunidades territoriales, cada una de las cuales participa del empleo industrial según las cuotas de participación x1, x2,...xM. Supongamos también que s1, s2, ...sM, sean la parte de empleo de una industria cualquiera que se encuentra localizada en una de las subunidades territoriales.
Otra medida tradicionalmente utilizada es el Índice normal de concentración geográfica o Índice de concentración MCO, pero se la descartó, pues no es más que una versión normalizada del Cociente de Concentración Geográfica Primaria. Sin embargo, se estimará también este índice para ver la robustez del resultado
Otra medida tradicionalmente utilizada del grado en que una industria difiere de la distribución espacial global del empleo industrial agregado es el índice primario de concentración geográfica:

Donde, de forma similar, xi refleja la proporción de cuotas agregadas de los sectores para la subunidad territorial i, y si refleja la participación en el empleo en la subunidad territorial i. Su valor oscila entre 0, que significa dispersión (o concentración espacial idéntica a la media de todas las industrias), y 1, que medirá la concentración (todo el sector se encuentra localizado en un territorio). El índice primario de concentración geográfica g no es más que una versión normalizada del índice G.
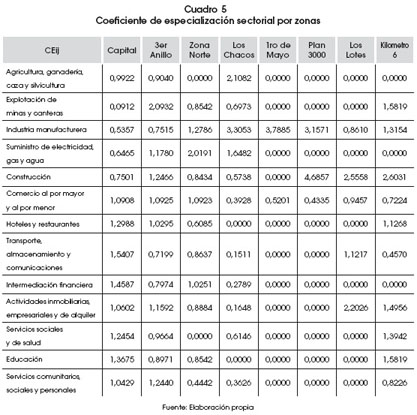
Respecto al índice de especialización, existen varios tipos de índices para medir el grado de diversificación de actividades en una ciudad, pero el más utilizado es el Coeficiente Regional de Especialización Sectorial, porque elimina todas las subjetividades de escala y es fácilmente adaptable a distintos ámbitos espaciales:
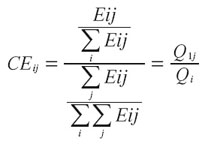
Donde:
Eij = Cantidad de empresas del sector de actividad i en el Anillo j
∑Ej = Cantidad de empresas total del Anillo j
∑E1 = Cantidad de empresas del sector de actividad i en el conjunto de Anillos (n)
∑∑En = Cantidad de empresas total en el conjunto de Anillos (n)
Sin embargo, este índice tiene una débil base teórica, por lo que se utiliza el Índice de Entropía Total utilizado por Sambharga (2000) junto con la Entropía no relacionada, pues permite distinguir las economías de localización (medida por la entropía total) de las economías de urbanización (medida por la entropía relacionada). Esta medida fue escogida por su “rigor técnico, base teórica fuerte y ausencia de subjetividad”. (Frenken et al., 2004). El índice de Entropía es simétrico12 entre las empresas, es insensible a las permutaciones de las porciones del mercado entre las empresas y satisface la condición de Lorenz, según la cual una expansión que preserve la media (es decir, una dispersión de la distribución de las porciones del mercado hacia los extremos) produce un incremento en el índice.
La Entropía Total se define de la siguiente forma:
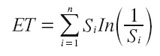
Donde S es la proporción o porcentaje de la i-ésima categoría, a cuatro dígitos, del Stándar Industrial Classification (SIC). Cuando ET tiende a 0, todo el empleo se concentraría en un solo sector, de forma que ET se maximiza al valor de ln(n), por lo que cuanto mayor sea el valor de ET, mayor su diversificación.
La Entropía No Relacionada se define como:
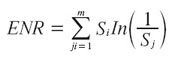
Donde j = 1…m, pero las categorías de los sectores del SIC están a solo dos dígitos, de forma que la medida es menor que la ET porque omite los sectores que están relacionados bajo una misma categoría.
Tenemos entonces que la Entropía Relacionada no es más que la Entropía total menos la Entropía no relacionada. Este índice está relacionado directamente con el grado de diversificación empresarial y está basado en tres elementos de la diversidad de la empresa: (a) el número de segmentos de producto en los que la empresa opera, (b) la distribución de las ventas totales de la empresa entre cada segmento de producto, y (c) el grado de relación entre varios segmentos de producto; tanto la medida de la entropía como el índice de Herfindahl recogen los dos primeros elementos, pero sólo la medida de entropía recoge el tercero de ellos (Palepu, 1985). De acuerdo con Waterson (1984) y Palepu (1985), el índice básico de entropía (ET) puede desagregarse en dos componentes: nivel de diversificación relacionada de la empresa (ER ) o entropía intergrupos, y nivel de diversificación no relacionada (ENR) o entropía intragrupos, siendo utilizado el sistema de clasificación estándar industrial (SIC) por esta medida para definir grupos de productos relacionados y no relacionados; así, productos que presentan SIC de cuatro dígitos distintos de industrias, pero que se encuentran dentro de los mismos SIC de dos dígitos de grupos industriales, son considerados relacionados (Hoskisson y Johnson, 1992).
4. Resultados
4.1. Localización y especialización dentro de la ciudad
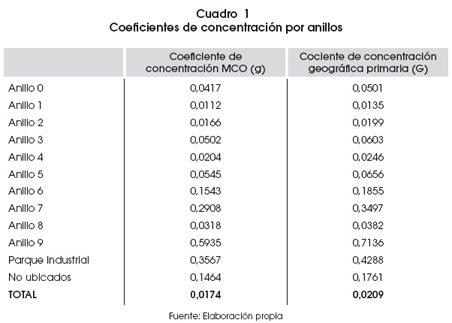
Los índices estimados muestran que hay una mayor concentración (especialización) de actividades en el anillo noveno, en el parque industrial (que llamaremos anillo 10 para simplificar), en los anillos 7, 6 y en los anillos 3 y 5. Los anillos que parecen tener más diversificación de actividades son los anillos 1, 2, 4 y, como era previsible, el anillo central o anillo 0 (tabla 1). En el mapa previo, los anillos están ordenados del centro para afuera, siendo el anillo 0 el centro, el primer anillo rojo el anillo 1, el segundo anillo rojo el 2, el anillo 3, el doble (interno y externo), y así hasta el anillo 9.
También se nota a primera vista que el índice escogido es más robusto que el índice de concentración MCO, por contar con valores menores que su homologo.
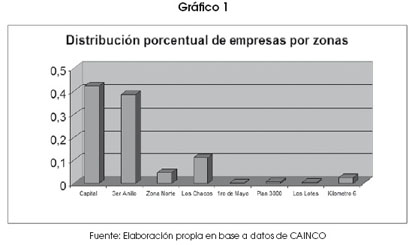
En relación con los subcentros, el subcentro Capital, conformado por los anillos 0, 1 y 2 tiene un 40% de las empresas de la ciudad y está muy diversificado. El subcentro 3er anillo, que lo rodea, comprende los anillos 3 y 4, y en él se concentra el 35% de las empresas de la ciudad. A partir de este subcentro, los subcentros se dividen en subcentros no circulares. El subcentro Los Chacos acapara con el 10% de las empresas, pero es interesante saber que este subcentro es básicamente el parque industrial con algunas unidades vecinales más, por lo que ese 10% genera la mayor producción departamental (Gráfico 1).
Gráficamente se observa que existe una mayor concentración empresarial en el centro o capital (conformado por el centro, el primer y el segundo anillo), que es casi igualada por las empresas en el tercer anillo. La zona “Los Chacos” contiene a toda la zona industrial, por lo que tiene una importante participación empresarial.
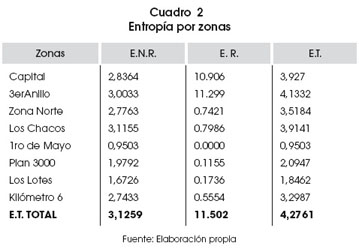
La Entropía Total (E.T.) estimada por zonas muestra que Santa Cruz tiene una alta especialización; sin embargo, las zonas que mayor Entropía Relacionada tienen son la capital y la zona del tercer anillo. (Tabla 2). De manera similar, el análisis de la entropía por anillos nos muestra un centro cuyas empresas se encuentran más relacionadas. Sorprendentemente, las empresas que más aprovechan los beneficios de localizarse cerca de su mercado antes que cerca de sus proveedores no son las que se encuentran más al centro, sino las que están entre el segundo y tercer anillo (tabla 3). Probablemente las empresas que están en el parque industrial no tengan una Entropía Relacionada elevada, por su escasa diversidad.

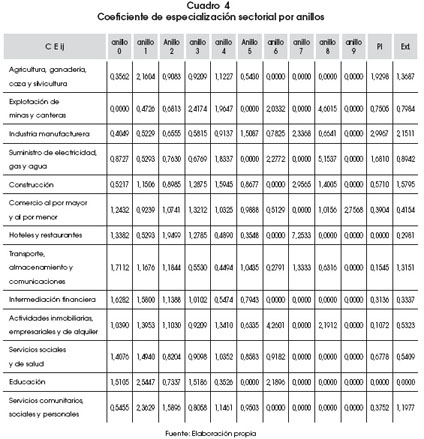
Los coeficientes de especialización sectorial calculados por anillo nos muestran una concentración de actividades terciarias en el centro, primer y segundo anillo. A medida que nos vamos alejando del centro, y tal como lo vimos anteriormente, las actividades se diversifican, observándose que las actividades más alejadas del centro son las más orientadas a las actividades primarias, como lo sugiere el modelo de la ciudad monocéntrica de Alonso. El sector de intermediación financiera se especializa dentro de los primeros tres anillos de la ciudad, como de forma similar lo hacen los servicios de salud y educación. El sector de agricultura tiende a especializarse en lugares alejados de la ciudad, aunque muchos cuentan con su casa matriz en el centro de la ciudad.
Lo mismo podemos observar en las zonas o subcentros planteados por el PLOT. Las mayores actividades terciarias se realizan en el primer anillo. La zona del tercer anillo muestra también una especialización en comercio y servicios. La zona Norte, Los Chacos, la zona primero de Mayo y el Plan 3000 muestran una especialización importante en industria manufacturera. Sin embargo, sólo la zona industrial en Los Chacos muestra una especialización de importancia en la exploración de soya y otros productos agropecuarios, al ser el parque industrial, donde se localizan las principales industrias de procesamiento agrícola departamental.
4.2. Contrastación de la hipótesis de policentrismo
Como se indicó previamente, se estima la variable dependiente como una aproximación de costo de transporte de transformación lineal de la densidad de empresas sobre la variable independiente, que es la distancia de cada unidad vecinal y la distancia estimada de dichas unidades vecinales al centro de la ciudad. La forma en que se estima esta distancia es por el anillo más próximo a cada unidad vecinal. Se estima que cada anillo tiene una anchura aproximada de un kilómetro.
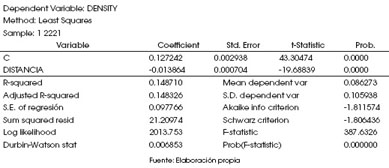
Dicha estimación, aunque tiene un muy bajo R2, se transforma en la estimación de la diferencial de las densidades (dij) entre la densidad empresarial de una unidad vecinal i y la densidad del centro j para la estimación de la ecuación de condición monocéntrica de Odland. La regresión estimada mediante MCO nos da coeficientes con signos congruentes con las variables teóricas.

Con las relaciones ya estimadas, comprobamos la hipótesis nula de monocentralidad de las empresas en la ciudad de Santa Cruz mediante un test de coeficiente conjunto de Wald.

Comprobamos que no se rechaza la hipótesis nula (que las empresas que se desarrollan en la ciudad de Santa Cruz se distribuyen espacialmente de forma monocéntrica).
5. Conclusiones
Las empresas en la ciudad de Santa Cruz de la Sierra continúan distribuyéndose espacialmente de forma monocéntrica. Un posible subcentro en formación es el parque industrial, que se especializa en actividades primarias y secundarias, las que se ven complementadas por las actividades especializadas en sectores de actividades terciarias del DCN.
Las empresas en la ciudad de Santa Cruz mantienen una cohesión cercana al centro de la ciudad. Esto muestra que las actividades se encuentran concentradas mayormente en los primeros tres anillos de la ciudad, por lo que se concluye que la ciudad de Santa Cruz es monocéntrica y su centro crece concéntricamente sobre su eje. La forma particularmente planificada de la ciudad contribuye a que las distancias recorridas al centro sean mínimas, lo cual colabora a mantener el centro sobre el centro histórico de la ciudad.
Se estimaron índices de concentración y se describió la localización de actividades según los subcentros y anillos propuestos, justificando que el Plan de Ordenamiento Territorial planifique una ampliación del área de la zona industrial hacia la zona de Villa Primero de mayo y Zona norte. De manera homóloga, incluir la zona del tercer anillo como parte de la zona de Santa Cruz Capital, ampliando así lo que se puede considerar el “centro” de la ciudad, tendrá un efecto similar
Los índices de especialización calculados corroboraron la localización teórica de actividades según modelos conocidos, como los de Alonso y Muth, y muestran la localización de las actividades en la ciudad para políticas de agrupación de actividades que posiblemente puedan ser implementadas por las autonomías.
También la Alcaldía de Santa Cruz puede incentivar la relocalización de empresas industriales de zonas cuya especialización es residencial hacia zonas más comerciales o industriales, mediante zonas con impuestos más reducidos o un pago de patente por contaminación para determinado tipo de empresas si se mantienen en esas zonas residenciales, como ser la zonas de Los Lotes y la zona Kilómetro Seis.
REFERENCIAS
Alonso, W. 1964. Location & Land Use. Cambridge, MA: Harvard U. Press [ Links ]
Anas, A. 1992. “On the Birth and Growth of Cities: Laissez-Faire and Planning Compared”. Reg. Sci. Urban Econ., 22:2, pp.243-58.
Anas, A. y K. Ikki. 1996. “GeneraI Equilibrium Models of Polycentric Urban Land Use with Endogenous Congestion and Job Agglomeration”. Journal of Urban Economics, 40:2, pp. 232-56.
Anas, Alex., R. Arnott & K. Small.1998. “Urban Spatial Structure”. Journal of Economic Literature, Vol. 36, No. 3, pp. 1426-1464. Sept.1998
Bacon, Robert. 1984. Consumer Spatial Behavior. Oxford, UK.: Clarendon Press. [ Links ]
Batty, M. y P. Longley. 1994. Fractal Cities: A Geometry of Form and Function. London: Academy Press. [ Links ]
Berliant, M. y K. Hideo. 1996. “The Endogenous Foundations of a City: Population Agglomeration and Marketplaces in a Location- Specific Production Economy”. Working paper, U. Rochester.
Bishop, P. y Peter Gripaios. 2007. “Explaining Spatial Patterns of Industrial Diversity: An Analysis of Subregions in Great Britain”. Urban Studies, 44:9,1739-1757.
Brueckner, J.K. 1979. “A model of non-central production in a monocentric city”. Journal of Urban Economics, Vol. 6, pp. 444.463
Christaller, W. 1966. Central Places in Southern Germany. London: Prentice-Hall. [ Links ]
Cervero, R. y W. Kang-Li. 1998. “Subcentering and Commuting: Evidence from the San Francisco Bay Area, 1980-1990”. Working Paper, Inst. of Urban & Regional Development, U. C. Berkeley.
CEBEC/CAINCO. 2004. “Aporte de Santa Cruz a Bolivia”. Versión preliminar, septiembre.
Coulson, E. y E. Bond. 1998. “A Hedonic Approach to Residential Succession”. Review of Economics and Statistics, 72(3). August, 433-444.
Duranton, G. y D. Puga. 2000. “Diversity and specialization in cities: why, where and when does it matter”. Urban Studies, 37(3), pp. 533–555
Ellison, G. y E.L. Glaeser. 1997. “Geographic Concentration in U.S. Manufacturing Industries: A Dartboard Approach”. Journal of Political Economics & Political Economics, 105:5, pp. 889-927.
Frenken, K., F.G. Oort, T. Van Verburg y R.A. Boschma. 2004. “Variety and regional economic growth in the Netherlands”. Final report to the Ministry of Economic Affairs, The Netherlands.
Getis, A. 1983. “Second-order Analysis of Point Patterns: The Case of Chicago as a Multi-Center Urban Region”. The Professional Geographer, 35-1, February, pp. 73-80.
Glaeser, E.L. et al. 1992. “Growth in Cities”. Journal of Political Economy, 100:6, pp. 1126-52.
Giuliano, G. y K.A. Small. 1991. “Subcenters in the Los Angeles Region”. Reg. Sci. & Urban Econ., 21:2, pp. 163-82.
Hamilton, B.W. 1982. “Wasteful Commuting”. Journal of Political. Economy, 90:5, pp. 1035-53.
Haig, R. 1926. “Toward understanding of the metropolis”. Quarterly Journal of Economics , XL 3 may 1936 and Regional survey of Ney York and its Environs NY city plan (1927).
Helsley, R.W. y W.C. Strange. 1991. “Agglomeration Economies and Urban Capital Markets”. Journal of Urban Economics, 29:1, pp. 96-112.
Henderson. V. y A. Mitra. 1996. “The New Urban Landscape: Developers and Edge Cities”. Journal of Regional Science & Urban Economics, 26:6, pp. 613-43.
Hoskisson, R. y R. Johnson. 1992. “Corporate Restructuring and Strategic Change: the effect on Divertification Strategy and R y D intensity”. Strategyc Managment Journal, 13, pp. 625-634.
Hotelling, H. 1929. “Stability in Competition”. Economic Journal, 39:1, pp. 41-57.
Hurd, R.M. 1903. Principles of city land values. New York: The recodan guide. [ Links ]
Instituto Nacional de Estadística (INE). Información recuperada de www.ine.gov.bo [ Links ]
Jacobs, J. 1969. The Economy of Cities. NY: Random House. [ Links ]
Krugman, P. 1991. Geography and Trade. Cambridge, MA: M.I.T. Press. [ Links ]
Krugman, P. 1991. “Increasing Returns and Economic Geography”. Journal of Political Economic, 99:3, pp. 483-99.
Krugman, P. 1993. “First Nature, Second Nature and Metropolitan Location”. Journal of Regional Science, 33:2, pp. 129-44
Krugman, P. 1996. The Self-Organizing Economy. Cambridge, MA: Blackwell. [ Links ]
LeRoy., S. y J. Sonstelie. 1983. “Paradise Lost and Regained: Transportation Innovation, Income, and Residential Location”. Journal of Urban Economics. 13: 1, pp. 67- 89.
Lungo, M. 1998. Gobernabilidad urbana en Centroamérica. San José. [ Links ]
Martin, R. y P. Sunley. 2003. “Deconstructing clusters, chaotic concept or policy panacea?”. Journal of Economic Geography, 3, pp. 5–35.
McMillen, Daniel P. y John F. McDonald. 1998. “Suburban Subcenters and Employment Density in Metropolitan Chicago”. J. Urban Econ., 43:2, pp. 157-80.
McDonald, J. 1987. “The Identification of Urban Employment Subcenters”. Journal of Urban Economics, 21:2, pp. 242-58.
McDonald, J. y P. Prather. 1994. “Suburban Employment Centres: The Case of Chicago”. Urban Studies, 31:2, pp. 201-18
McDonald, J. y H. Woods Bowman. 1979. “Land value functions: A reevaluation”. Journal of Urban Economics, Vol. 6, pp. 25.41,
Mills, E. 1972. Studies in the Structure of the Urban Economy. Baltimore: Johns Hopkins Press. [ Links ]
Moses Leon y Harold Williamson, Jr. 1967. “The Location of Economic Activity in Cities”. American Economic Review., 57:2, pp. 211-22.
Muth, R. 1969. Cities and Housing. The U. of Chicago Press, Chicago [ Links ]
Odland, J. 1978. “The Conditions for Multi-Center Cities”. Economic Geography, Vol. 54, No. 3
Oh´Uallachain, B. 1989. “Agglomeration of Services in American Metropolitan Areas”. Growth & Change, 20:3, pp. 34-49.
Papageorgiou, G. y H. Mullally. 1976. “Urban Residential Analysis: 2. Spatial Consumer Equilibrium”. Environment and Planning, 8, pp. 489-506.
Palepu, K. 1985. “Diversification Strategy, Profit Performance and the Entropy Measure”. Strategic Management Journal, Vol 6, 239-255
Pérez, S. y M. Polèse. 1996. Modelos de análisis y de planificación urbana. Estudio sobre la evolución y tendencias de la ciudad de Puebla. 1a. ed., Plaza y Valdés, México. [ Links ]
Polése, M. 1998. Economía urbana y regional. Introducción a la relación entre territorio y desarrollo. 1a. ed., Libro Universitario Regional, Costa Rica. [ Links ]
Prado-Salmón, F. Plan estratégico de desarrollo municipal. Reformulación del PDMS 2010 e integración con el PLOT y los planes sectoriales. [ Links ]
Richardson, H. 1977. “The New Urban Economics: An Evaluation Socio-Economic”. Planning Sciences, 10, pp. 137-47.
Romer, P. 1986. “Increasing Returns and Long-Run Growth”. Journal of Political Economics, 94:5, pp. 1002-37.
Rosen, K. y M. Resnick. 1980. “The Size Distribution of Cities: An Examination of the Pareto Law and Primacy”. Journal of Urban Economics, 8:2, pp. 165-86.
Sambharya, R. B. 2000. “Assessing the construct validity of strategic and SIC-based measures of corporate diversification”. British Journal of Management, 11, pp. 163–173.
Thomas, R.W. 1981. “Point Pattern Analysis”. En: N. Wrigley and R. J. Bennett (eds.): Quantitative Geography: A British View. London: Rout-ledge & Kegan Paul, pp. 164-76
Von Thunen, J. 1826. Der isolerte Staat in Beziehung auf Land, Wirtschaft und Nationalökonomie. Hamburg: F. Perthes 1st vol 3d vol 1863. [ Links ]
Von Boventer, E. 1976. “Transportation Costs, Accessibility and Agglomeration Economies: Centers, Subcenters, and Metropolitan Structure”. Papers, Regional Science Association, 37, pp. 167-83.
Waterson, M. 1984. Economy theory of the industry. Cambridge: Cambridge University Press. [ Links ]
White, M. 1976. “Firm Suburbanization and Urban Subcenters”. Journal of Urban Economics, 3:4 pp. 323-43.
1 Para tres útiles formas de especificación de subcentros especializados en bienes complementarios, suplementarios o independientes, ver Anas et al. (1998: 1442)
2 Dicho planteamiento asume que las empresas de actividades de pérdida de peso se sitúan en la periferia y las empresas de actividades de ganancia de peso se sitúan en el centro.
3 El régimen autonómico fue avalado por el referéndum de febrero del 2006 y sus estatutos avalados en el referéndum de febrero 2007. En la actualidad, la nueva Constitución Política del Estado avalada en el referéndum de enero 2009 también hace referencia a las autonomías, aunque las competencias y políticas de implementación aun están siendo discutidas.
4 Una zona específica puede ser planteada como una zona con amenidades empresariales, que puede o no coincidir con las amenidades residenciales, o una zona donde localizar ciertas empresas de mayor impacto potencial en empleo o que necesiten de condiciones para mitigación ambiental.
5 De acuerdo a las tendencia del crecimiento de la población, el INE estima que el departamento alcance 2,4 millones de personas para el 2005 (con una tasa de crecimiento de 4.87% para 2001-2005) y 3.1 millones en el 2010 (con tasa de crecimiento de 4.98% para 2005-2010), siendo para entonces el departamento más poblado del país.
6 El Distrito Central de Negocios (DCN) se define como la principal “área central” de la ciudad, que presenta la más alta concentración de servicios a la producción y otros servicios superiores y de funciones comerciales (Pérez y Polèse, 1996).
7 Un fractal es la resultante de un proceso limitado que se repite reiteradamente cuanto menor es la medida de la distancia.
8 El Point Pattern Analysis se basa en definir estadísticos de distancia entre unidades y las compararlas con distribuciones teóricas tales como la postulada por Christaller (1966) o la de Alonso (fecha) y Muth (fecha).
9 La derivada es supuesta menor a cero para permitir las economías de aglomeración, y se asume que los costos de producción son independientes de los niveles de producción de otras zonas (derivada cruzada igual a cero)
10 Su primera derivada es mayor a cero, tal que esa pérdida de ingreso real per cápita se incrementa con el tamaño de la población de una zona, y que los efectos de la congestión poblacional no son percibidos por las personas, siendo su derivada cruzada igual a cero.
11 Se hace que uno de los supuestos aleje a la empresa al anillo más próximo y el otro acerque a la empresa al anillo más próximo.
12 La concentración para empresas simétricas debe decrecer cuando el número de ellas aumenta de n a n + 1
Anexos
Anexo 1: Unidades vecinales contenidas en nuevas centralidades

Anexo 2: Desarrollo matemático del modelo de Odland
El modelo determina el orden espacial de la ciudad al localizar niveles productivos y densidades poblacionales en un conjunto limitado de zonas y determinando un número de conmutantes entre cada par de zonas en un patrón que minimiza la suma de los costos de producción, costos de transporte de los conmutantes y las pérdidas de ingreso reales por el aumento residencial. Formalmente, la función objetivo:
![]()
está sujeta a:
![]()
![]()
![]()
![]()
Las condiciones Kuhn-Tucker para la solución optima se obtienen de las derivadas del Lagrangiano, tal que:
para todo i;

para todo j;
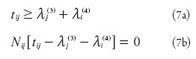
para i y j;

Las condiciones (6), (7) y (8) determinan, para una solución óptima, la distribución del empleo, actividad residencial y conmutación, respectivamente. Para que la zona j sea un centro de empleo la condición (6a) debe mantener la igualdad y el nivel de producción será determinado como el valor de QJ que soluciona:
![]()
De manera similar con la condición (8a), que se mantiene en igualdad como parte de la solución óptima entre las actividades residenciales en la zona i determinada como el valor Pi que soluciona:
![]()
Finalmente, la condición (7a) tiene que mantener su igualdad si el flujo de conmutantes de la zona i a la zona j es parte de la solución óptima.
![]()
Para hallar la condición de una ciudad monocéntrica, se supone que todo el empleo es concentrado en un zona que llamaremos a partir de ahora DCN, que, al igual que en (9), se mantiene en igualdad y en desigualdad para el resto de las zonas:
![]()
Dado que la producción del DCN es la producción de toda la ciudad, la solución óptima localizará las demás personas fuera del DCN a un número M de zonas residenciales. La condición (8a) se mantendrá en igualdad para todos los miembros de las M zonas:
![]()
y dado que todos los conmutantes lo harán de las M zonas al DCN, la condición (11) se mantendrá en igualdad para esos viajes para todo i є M:
![]()
Las igualdades (13 y (14) pueden ser sumadas para cada zona de M:
![]()
Esta ecuación tan sólo especifica la distribución de la población que se asocia con una ciudad de forma monocéntrica. Una condición para mantener la forma monocéntrica puede ser obtenida al añadir las condiciones (12) y (15). Estas dos ecuaciones pueden ser sumadas en pares de zonas, que tiene un miembro del set M como origen y al DCN como destino. El resultado cancelando términos es:
![]()
Esta ecuación también puede ser sumada para los m miembros del set de zonas M:
![]()
Esta relación sólo se mantiene para una ciudad monocéntrica. Pero para una ciudad que no es monocéntrica, la igualdad se transforma en una inequidad “Mayor a”.














