Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Fides et Ratio - Revista de Difusión cultural y científica de la Universidad La Salle en Bolivia
versión On-line ISSN 2071-081X
Fides Et Ratio vol.26 no.26 La Paz set. 2023
ARTÍCULOS ORIGINALES
Estimación y análisis de
estabilidad del modelo de
crecimiento económico de
Solow para el Perú
Estimation and stability analysis of the
Solow model of economic growth for Perú
Luis Francisco Laurente Blanco1![]()
1 Ingeniero Economista, Maestro en Informática. Profesor e Investigador
de la Universidad Autónoma de lea (UAI), Chincha Alta, lea, Perú.
flaurenteblanco@gmail.com
Artículo Recibido: 22-02-2023 Artículo Aceptado: 05-07-2023
Resumen
Este artículo evalúa los parámetros del modelo de Solow para el Perú en el periodo de crisis internacional y pandemia del COVID-19. Las estimaciones utilizan modelos de largo plazo con información del Banco Central del Perú (BCRP). Los resultados muestran que el efecto del capital en la producción de largo plazo no sufrió variaciones importantes durante la crisis internacional. Durante el COVID-19, los parámetros del modelo se mantuvieron estables a pesar de las drásticas medidas implementadas por el Gobierno que afectaron a la producción. Las políticas realizadas por el Gobierno y el BCRP durante la pandemia fueron decisivas para la recuperación económica.
Palabras clave: Análisis de estabilidad, COVID-19, crisis internacional, modelo neoclásico.
Abstract
This article evaluates the Solow model parameters for Perú in the period of international crisis and COVID-19 pandemic. The estimates use long-term models with information from the Central Bank of Perú (BCRP). The results show that the effect of capital on long-term production did not suffer significant variations during the international crisis. During COVID-19, the model parameters remained stable despite the drastic measures implemented by the Government that affected production. The policies carried out by the Government and the BCRP during the pandemic were decisive for the economic recovery.
Keywords: COVID-19, international crisis, Neoclassical model, stability analysis.
JEL Classifications: C32, C51, F41
Introducción
Los diversos shocks que ocurren en el mundo son adversos al crecimiento del PBI peruano de largo plazo, es el caso de la crisis financiera de 2008-2009 que trajo una reducción importante en el crecimiento del producto potencial o de largo plazo. Por otro lado los diversos shocks de demanda también mostraron efectos adversos importantes en el comportamiento del producto. Asimismo, en marzo de 2020 comienza el Estado de Emergencia en el Perú debido a la pandemia mundial COVID-19 la misma que paralizó la producción pues la medida incluía cierre de fronteras y aislamiento obligatorio que impedía el tránsito normal de la producción (Laurente, 2021). Estos shocks que tienen efectos en el producto según su intensidad muchas veces pueden generar fluctuaciones importantes y estos por su intensidad casi nunca son autocorregibles mas bien son efectos que podrían quedarse para siempre en una economía (Jiménez, 2018). Frente a esto es deber de la autoridad monetaria y del Gobierno contrarrestar estos impactos y en otros casos corregirlo mediante la aplicación de políticas económicas que permitan retornar al comportamiento de largo plazo del producto.
En el estudio del crecimiento económico del producto de largo plazo, existen dos principales enfoques que la estudian. El primero es el enfoque debido a la demanda. En este enfoque se encuentra dos modelos que la explican, el modelo de Shaikh y Moudud (2004) que es una ligera modificación en el cambio tecnológico del modelo de Kaldor (1957) y el modelo de Thirlwall (1979) donde explica que el crecimiento del producto de largo plazo se determina por las exportaciones de la economía o lo que es lo mismo determinada por la demanda externa como su principal determinante.
El segundo enfoque es el de oferta conocido como el modelo neoclásico de Solow-Swan (1957). Este enfoque sostiene que el crecimiento de una economía está determinado por factores de oferta como son los factores de producción exógeno capital y trabajo.
Para el caso peruano, Céspedes (2014) señala que los determinantes del PBI potencial antes de la crisis internacional de 2008-2009, fueron la inversión (capital), el nivel de empleo y la productividad; esos determinantes fueron muy importantes en la década pasada. Tras la crisis todos estos factores sufren un comportamiento decreciente, además como factores del PBI potencial se reducen a la inversión y la productividad los cuales al desacelerarse provocaron un efecto persistente para reducir el crecimiento del PBI potencial. Uno de los principales causantes de la desaceleración de la productividad fue el sector externo mediante una importante disminución de los términos de intercambio que tiene efectos de corto y largo plazo en la productividad. El producto potencial peruano depende de determinantes estructurales y de coyuntura que contribuyen en el efecto de largo plazo en el crecimiento del producto. El producto potencial ha experimentado un importante quiebre estructural debido a la crisis internacional de 2008-2009, lo que para años posteriores presenta un comportamiento decreciente debido a disminuciones importantes de la inversión que a su vez disminuyó la acumulación de capital. Por otro lado, el crecimiento de la productividad la misma que afecta el uso eficiente de los factores de producción, también sería el causante de la reducción del producto potencial peruano. La reducción del PBI potencial peruano tras la crisis fue decreciente y sus importantes determinantes como son la inversión, el empleo y la productividad presentaron el mismo comportamiento. Luego, como señala Jiménez (2017) para recuperar el crecimiento del producto de largo plazo en el Perú es necesario estimular reformas estructurales que incrementen el crecimiento de la inversión y la productividad.
El objetivo del trabajo es hallar los valores de los parámetros del modelo de Solow para el Perú prestando atención al período de crisis internacional y la presencia de la pandemia COVID-19- El período analizado corresponde a una frecuencia mensual de 2001m5-2022ml2. Debido que el estudio es para la producción de largo plazo, se utiliza el método de cointegración de Gregory-Hansen para estimar la existencia de cointegración de largo plazo con presencia de quiebre estructural entre las variables del modelo. El resto del documento se organiza de la siguiente forma: la sección 2 presenta la revisión de la literatura; la sección 3 discute la metodología del modelo. La sección 4 presenta los resultados de las estimaciones y la sección 5 las conclusiones más relevantes de la investigación.
Revisión de literatura
En la estimación y aplicaciones empíricas del modelo de Solow se utilizan diversas técnicas econométricas para verificar el valor de sus parámetros. En el trabajo de Boyko et al (2020) se utiliza regresión lineal para estimar los parámetros del modelo de Solow para Rusia. En sus resultados señalan que el modelo de Solow y el modelo de producción de Cobb-Douglas aproximan adecuadamente la información. Los parámetros que se estimaron fueron: el proceso de innovación, el nivel de tecnología, elasticidad del trabajo y la elasticidad del capital. Los resultados de la estimación muestran que el trabajo y el capital tienen un efecto directo sobre la función de producción. Por su parte Barossi-Filho, Silva y Diniz (2005) estudian la evidencia empírica del modelo de Solow. En su análisis utilizan test de raíz unitaria para datos de panel y la estimación de cointegración para evaluar la existencia de ecuaciones de largo plazo. En la estimación hacen uso del método de mínimos cuadrados dinámicos y reportan la existencia de una estructura de capital sobre el ingreso en el largo plazo. Gutiérrez et al (2004) estudian el modelo de Solow y aplicaciones en la economía colombiana.
En sus resultados reportan que las fuentes de un crecimiento económico son todavía un tema de gran debate en un país. Señalan que la tasa de crecimiento según el modelo de Solow es exógena y no dependería de la inversión o del sistema tributario y que el ahorro tras alcanzar su estado estacionario a una tasa dada, cualquier política que incentive el ahorro no tendrá más efecto sobre el crecimiento económico en el largo plazo. Concluyen que para que el país incremente su crecimiento se debe aplicar políticas que incentiven el uso de capital humano y físico; y buscar principalmente un proceso simultáneo entre estos factores de producción. Rosas (2017) realiza una estimación del modelo de Solow-Swan para los países de la OCDE. Para sus resultados usa la metodología de estimación transversal para analizar los determinantes del crecimiento económico para estos países usando el modelo de Mankiw. Reporta que el modelo de Solow aumentado o de Mankiw donde se ajusta el crecimiento del PBI per cápita y sus determinantes capital físico, fuerza laboral y acumulación de capital humano, tiene un buen ajuste para la información de los países y que estos convergen aproximadamente según el modelo de Mankiw. Para el caso peruano, Jiménez (2018) estudia el producto de largo plazo y su brecha desde dos enfoques distintos; desde el enfoque de demanda y el enfoque de oferta según el modelo neoclásico Solow-Swam. En su estimación utiliza técnicas de cointegración para verificar la existencia de relaciones de largo plazo entre sus variables. En sus resultados de los modelos señala que las políticas aplicadas a la demanda afectan a la capacidad de la economía en el largo plazo. Según las estimaciones del modelo de Solow reporta que la demanda no tiene efecto sobre el producto potencial y que sólo influye en las fluctuaciones del producto.
Willington (1998) estudia el crecimiento regional y sus determinantes en Argentina con especial tratamiento en el contraste de la hipótesis de convergencia. En sus resultados señala que para el caso de las regiones argentinas la variable stock de capital humano es la única que explica significativamente al crecimiento per cápita en el período de estudio. Además señala que cada provincia converge a su estado estacionario a una velocidad distinta del resto de las provincias. Hoeffler (2000) estudia el modelo de Solow y su aplicación para África. En su resultado señala que el modelo aumentado de Solow puede aproximar completamente el crecimiento de África siempre que se tenga en cuenta los efectos a los países no observados y para la endogeneidad de la inversión en la estimación. Por su parte, Magnani (2013) estudia el modelo de Solow prestando atención al desempleo. En sus resultados reporta que un incremento en la demanda agregada debido a un incremento en el gasto público o en la tasa de ahorro, reduce el desempleo lo que estimula una variación positiva en el PBI, así el modelo de Solow tiene un efecto intermedio en estimular la variación del producto. Por su parte, Ibarra (2018) aplica el modelo de Solow para estudios ambientales y de reciclaje utilizando la premisa que la materia prima, así como el trabajo y el capital, tiene un efecto importante en el crecimiento económico. Señala además que al considerar el reciclaje en el modelo de Solow, el impacto se refleja en un mayor nivel de capital debido al incremento de la materia prima disponible y el reciclaje que permite la reutilización y la disminución de la contaminación en el largo plazo en un determinado proceso productivo. Así en términos del modelo de Solow, el reciclaje sería equivalente a una mejora en la tecnología lo que desplaza la función de producción. En aplicaciones de ecuaciones diferenciales ordinarias para economías dinámicas que aproximan el crecimiento económico, capital y ciclos de las transacciones comerciales entre países, se encuentra el trabajo de Tsoularis (2021) que modela con el uso de ecuaciones diferenciales el comportamiento de la producción. En su trabajo no toma en cuenta los modelos de ecuaciones diferenciales para modelos de caos y bifurcaciones económicos.
Metodología
A. Especificación del modelo
El modelo de Solow estudia tres variables de interés: el producto (Y), el capital (K) y el trabajo (L). La función de producción está formulada a partir de la oferta en la economía y su relación con los factores de producción. Está dada por la siguiente expresión
![]()
donde el término expresa el tiempo que está analizada las variables. Esta función de producción se denomina neoclásica cuando no se considera algún progreso tecnológico. A continuación se estudia las condiciones que cumple la función de producción:
(a) Función de producción. La función de producción es dada por Y=F (K, L) es la cantidad de bienes producidos por K unidades de capital y L unidades de trabajo en un determinado período de tiempo. En una economía cerrada donde el total de la producción es la inversión y consumo, la producción es
![]()
donde C(t) representa la función de consumo e I(t) es la inversión en el período t. Un importante supuesto en el modelo son las condiciones de Inada (1963) para valores K> 0 y L > 0, dado por
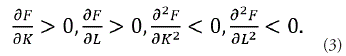
Las primeras dos condiciones indican que el capital Ky el trabajo tienen efectos positivos sobre la producción y las siguientes condiciones indican que estos incrementos son decrecientes. Evaluando en el límite las condiciones de Inada se tiene
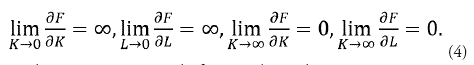
Estos límites aseguran que la función de producción F es estrictamente cóncava con pendiente decreciente que va desde infinito cuando L, K -> 0 a una pendiente cero cuando L, K -> ∞. La otra condición de Inada indica que la función de producción F es lineal y homogénea de grado 1 en los factores Ky L, esto es
![]()
a este valor de homogeneidad se conoce como retornos constantes a escala que no es otra cosa que cualquier incremento en el capital y trabajo resultando en un incremento proporcional al nivel de producción. En particular, dado que la hipótesis de retornos constantes se puede simplificar en la función de producción; esto es, si seleccionamos ![]() y fijando el nivel de producción por trabajador como
y fijando el nivel de producción por trabajador como ![]() y el nivel de capital por trabajador como
y el nivel de capital por trabajador como ![]() , se tiene
, se tiene
![]()
La función de producción está expresado en términos del trabajo y capital por unidad de trabajador. Esta simplificación de la función de producción se denomina función intensiva e indica que la cantidad de producción por trabajador depende únicamente de la cantidad de capital por trabajo y no de la economía en general. Esta función intensiva f(x) no cumple con la homogeneidad lineal de las condiciones de Inada.
(b) Crecimiento del capital K en la economía. El crecimiento del stock de capital K es equivalente al crecimiento de la inversión I la cual es usada para incrementar el capital sujeto a la depreciación. La inversión es igual a la suma de la tasa de variación del capital y la tasa de depreciación del capital,
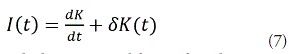
donde δ es la tasa de depreciación del capital. Si denotamos como c(t) e i(t) como el consumo e inversión por unidad de trabajo, se tiene
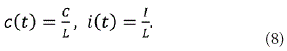
Entonces el nivel de producto por unidad de trabajo es
![]()
(c) Función de producción de Cobb-Douglas y de Solotv. La función de producción Cobb-Douglas se escribe como
![]()
donde Yes la producción, K es la cantidad de capital usado, L costo del trabajo, A es el coeficiente de producción, α es una constante que representa la elasticidad del producto respecto al capital y la constante β representa la elasticidad del producto respecto al trabajo. El coeficiente de producción A está asociado con el nivel de tecnología y otros factores distintos al capital y trabajo. En general este coeficiente se considera en función del tiempo aunque para propósitos de estimación se considera como una constante.
El modelo de crecimiento económico de Solow se basa en la función de producción Cobb-Douglas con la particularidad que el progreso tecnológico y científico se encuentra dentro de la ecuación como un factor de crecimiento a parte del capital y el trabajo. La evolución del tiempo es el factor dado por eγΔt donde el valor de Y caracteriza el grado del progreso científico y tecnológico. El factor eγΔt caracteriza la introducción de procesos de innovación en la economía y además la introducción de este coeficiente reduce el efecto asociado a la tendencia determinística en las variables. La función de producción de Solow está dada por
![]()
El modelo describe la influencia de los factores capital, trabajo e innovación tecnológica sobre el crecimiento económico donde el progreso en ciencia y tecnología depende del tiempo. Cuando γ=U el progreso tecnológico es cero y el modelo de Solow es la función de producción de Cobb-Douglas. El valor de γ = 0 indica también la ausencia del tiempo. Para aplicaciones empíricas de la ecuación, las variables se obtienen de las estadísticas y los coeficientes del model A,α,β,γ son calculados en la estimación. Para calcular los retornos a escala del modelo de Solow de la ecuación (11) se calcula la operación α + β y los retornos son los siguientes: si α + β < 1 los retornos son decrecientes a escala, α + β = 1 los retornos son crecientes a escala y α + β > 1 los retornos son crecientes a escala. En particular, los retornos son crecientes a escala cuando un incremento en una unidad de los factores permite que el nivel de producción se incremente en más de uno. Para estimaciones econométricas, la ecuación (1) queda determinada como la siguiente ecuación:
![]()
donde los términos θ son los parámetros de largo plazo del modelo de producción.
B. Datos
Las variables que se utilizan en la investigación corresponden al producto (Y), stock de capital (K) y el trabajo (Z). Para obtener la información se realizó una exploración de las estadísticas del Banco Central del Perú (BCRP, 2022) disponible en la página web de la institución y que es de uso público. Para el factor trabajo (Z) se utilizó el promedio móvil de tres meses de la PEA ocupada en miles de personas. Para la variable stock de capital (K) se utilizó la información de la liquidez de las empresas bancarias en moneda nacional de las obligaciones a plazo en millones de soles y de las obligaciones a plazo de la liquidez del Banco de la Nación en millones de soles y posteriormente se realizó una suma entre estos valores para obtener la variable. Para la variable producto (Y) se utilizó la información del producto bruto interno en millones de dólares. Para su conversión en la moneda local, se utilizó la información del tipo de cambio interbancario sol-dólar promedio del período y se realizó la multiplicación con la información del producto en dólares obteniéndose esta información en la moneda local. Se considera información de frecuencia mensual en el período mayo de 2001 (200Im5) hasta diciembre de 2022 (2022ml2) con un total de 260 observaciones, que es más conveniente que la utilización de información trimestral pues permite una mejor aproximación en los tests estadísticos a usarse. Todas las variables se calculan en escala logarítmica con la finalidad de linealizarlas y mantenerlas en una escala más homogénea. Adicionalmente al empleo de los test de significancia para los modelos se considera tres hipótesis de interés de la ecuación (11). La primera corresponde a los rendimientos constantes a escala en el largo plazo H0 α + β = 1. La segunda a los rendimientos decreciente a escala en el largo plazo H0 α + β < 1 ; y la tercera hipótesis corresponde a los rendimientos crecientes a escala en el largo plazo H0 α + β > 1.
Resultados empíricos
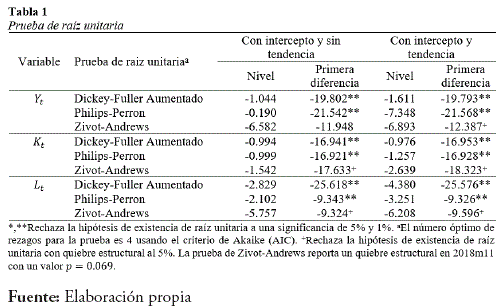
Para encontrar la relación de largo plazo o de cointegración entre las variables, se debe probar que las series producción (F), stock de capital (iT) y trabajo (L^ son integradas de orden uno /(I). Para ello se evalúa mediante la prueba de raíz unitaria a las series calculadas en niveles para intercepto y sin tendencia e intercepto con tendencia; y en primeras diferencias usándose las pruebas de Dickey-Fuller Aumentado (Dickey y Fuller, 1979), Phillips y Perron (1988) y Zivot y Andrews (1992), este último analiza la hipótesis de raíz unitaria con quiebre estructural. Para analizar los rezagos a utilizar, se hace uso del criterio de Akaike (AIC) la cual señala que 4 es el número de rezagos máximos a utilizarse para estas series. En la Tabla 1 se muestra los resultados de la aplicación de los test de raíz unitaria, donde se reporta la existencia de una raíz unitaria para las series en niveles ya sea con intercepto sin tendencia y con intercepto y tendencia. Para el análisis de las series en primeras diferencias, la tabla muestra que para las series se rechaza la hipótesis de raíz unitaria, por lo tanto debido a estos resultados se tiene que las series analizadas son o integradas de orden uno. Similares resultados se encontró con el test de raíz unitaria de Zivot y Andrews (1992) donde muestra que las series son integradas de orden uno y con la existencia de un quiebre estructural en 2018mll con un valor p=0.069 aceptando la hipótesis nula de raíz unitaria con quiebre estructural.
Para el análisis de cointegración de las variables se utiliza el test de Gregory y Hansen (1996) de cointegración con quiebre estructural donde se tiene la hipótesis nula que no existe cointegración en el punto de quiebre. Esta prueba señala que se rechaza la hipótesis nula si el valor absoluto de los estadísticos es mayor que el 5% valor crítico. Los resultados de la aplicación del test se muestran en la Tabla 2, en ella reporta que un valor del estadístico ADF de -6.09 mayor al valor crítico en valor absoluto de -5-50 al 5% lo que evidencia un quiebre estructural en fecha 2018ml0. Por otro parte, los estadísticos calculados de Phillips Za y Zt indican la existencia de un quiebre en 2018m9 a un valor crítico de 5%. En consecuencia, se incluye una variable artificial (D) con valores iguales a cero en el periodo 200 Im5-2018m9 e igual a uno para el período 2018ml0-2022m12.
Considerando la variable artificial, la ecuación de cointegración que se somete a prueba a partir de la ecuación (12) es la siguiente
![]()
donde Yt es el producto, t es la tendencia, Kt es el stock de capital, D es la variable dummy que capta el quiebre estructural, Lt es el empleo. En consecuencia los parámetros θ0,θ1,θ2 y θ3 de la ecuación (12) que son calculadas para el período antes y después del quiebre y se expresa como el siguiente sistema
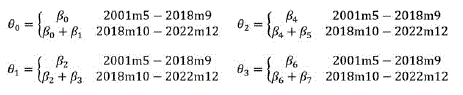
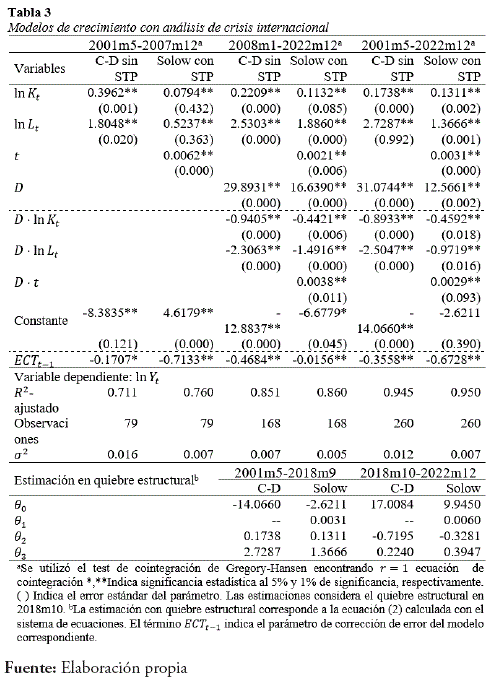
Para la estimación de la ecuación anterior se utiliza cuatro rezagos según el criterio de Akaike y el método de estimación de las ecuaciones de largo plazo es el de mínimos cuadrados completamente modificados (FMOLS). La Tabla 3 muestra los modelos de crecimiento de la ecuación (13) para el análisis de crisis internacional. Para la estimación se considera tres estimaciones que corresponden al período antes de la crisis (200Im5-2007ml2), período pos-crisis 2008ml-2022ml2 y una estimación que considera ambos períodos (2001m5-2022ml2). Además en cada período se hace uso de un modelo de Cobb-Douglas que no considera cambio tecnológico (STP) y un modelo de Cobb-Douglas con cambio tecnológico denominado como el modelo de Solow.
La primera columna de la Tabla 3 muestra las variables consideradas en la ecuación (13), los efectos cruzados de la variable dummy y el coeficiente de ajuste ECTt; del modelo de corrección de error. Se muestra también los estadísticos y los parámetros de la ecuación (12) que son calculados según el sistema de ecuaciones. Las siguientes columnas muestran las estimaciones de la ecuación (13) para los períodos antes y después de la crisis internacional. Las estimaciones muestran que todas las variables son significativas al 1% de significancia y en la estimación del modelo de corrección de error, el parámetro ECTfl que indica la velocidad de convergencia, se observa que este valor es menor de cero y estadísticamente significativo para todos los modelos lo que muestra que existe esta convergencia entre el corto y largo plazo, así los modelos de largo plazo son estables. Al analizar las estimaciones se observa que el nivel de capital en el período antes de la crisis habría sido ligeramente menor al período poscrisis. Asimismo, en la estimación considerando el total de la muestra, el capital no muestra una variación importante. Con esto se puede pensar que el efecto del nivel de capital sobre la producción no habría sido muy afectada en el largo plazo para la economía peruana. Por otro lado, el efecto del empleo en la producción en el período antes de la crisis habría sido menor que el período poscrisis, lo que muestra que el nivel de empleo ha sido una variable importante para regresar al nivel de producción a su nivel de largo plazo tras sufrida una crisis, lo que nos deja evidencia que tras una crisis es necesario incentivar el empleo debido que esta variable puede tomar importancia para mejorar las condiciones de la producción.
Para verificar los parámetros de los modelos con el quiebre estructural se utiliza la ecuación (13), y las ecuaciones del sistema. Este cálculo se muestra en la parte inferior de la Tabla 3, se observa que respecto al tiempo, el parámetro Q1 del modelo de Solow tuvo un ligero incremento tras el quiebre, lo que muestra que el tiempo en ambos períodos de análisis estaría teniendo un ligero efecto sobre el crecimiento de la producción. Respecto al parámetro O2 que captura el efecto del capital sobre la producción, se observa una variación importante para ambos modelos Cobb-Douglas y Solow. Esta variación de pendiente muestra que efectivamente el quiebre de 2018ml0 tuvo variación en los parámetros, es decir, que en el período antes del quiebre el efecto que tenía el capital sobre la producción era positivo para ambos modelos y el efecto para el período 2018ml0-2021ml2 fue inverso. De este modo el período 2018ml0 de quiebre habría sido muy importante para la variación de los parámetros del modelo en la economía peruana.
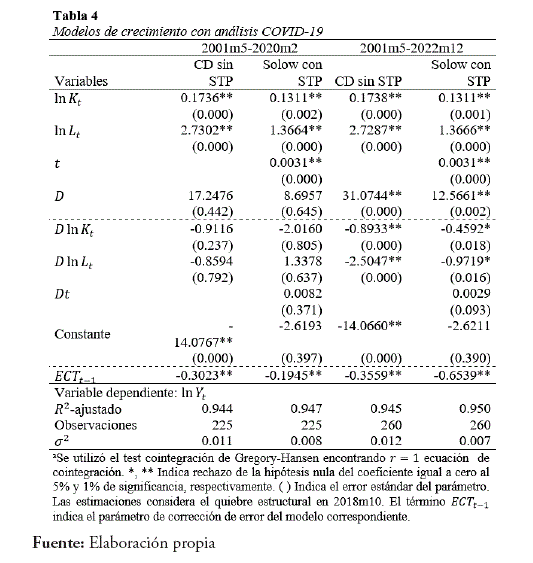
Para conocer el comportamiento del modelo de Solow debido al COVID-19, la Tabla 4 muestra la estimación de los coeficientes de la ecuación (12) y (13) para los períodos de estimación antes de la pandemia y estimación con muestra completa. Las estimaciones muestran que todas las variables son significativas al 1% de significancia y el coeficiente de corrección de error ECTc ¡ es estadísticamente significativo y menor a cero mostrando la convergencia entre el corto y largo plazo. Los resultados muestran que los parámetros de los modelos para ambos períodos no variaron significativamente para las variables consideradas. Este resultado es interesante debido que el Perú durante la pandemia de COVID-19 ha implementado acciones rígidas que afectaron a la economía en el país ya que se paralizó todas las actividades productivas y de servicios dejando al país en cuarentena obligatoria por varios meses (MINCETUR, 2020). Al parecer las acciones inmediatas del Gobierno y del Banco Central (BCRP) de apoyo al sector productivo habrían tenido mucha influencia para mantener el nivel de producción sin una variación importante en el largo plazo (ADEX, 2020; Montoro, 2020). En este sentido, la implementación de las políticas monetarias y fiscales en el Perú durante el período de pandemia han sido determinantes para contrarrestar el impacto ya que estas habrían permitido una cierta estabilidad en el comportamiento de largo plazo de las variables consideradas (Gamero y Pérez, 2020).
Haciendo una comparativa de las estimaciones para evaluar el efecto de la crisis internacional y el COVID-19, se puede concluir que la crisis internacional tuvo un efecto mayor sobre los parámetros de los modelo de Solow en comparación con el período de pandemia, aunque las condiciones de la economía en ese período no fueron las mismas que las condiciones económica previas a la pandemia donde el país estaba robusto respecto a indicadores macroeconómicos. Luego, las rápidas acciones realizadas por el Gobierno en coordinación con el Banco Central durante la pandemia fueron determinantes y con certeza sirven como aprendizaje para futuros shocks de demanda o de oferta que pueda afectar al Perú.
Discusión
En el análisis comparativo de las estimaciones del modelo de Solow para el Perú se determinó que el nivel de capital en el período antes de la crisis habría sido menor al período poscrisis, esta diferencia no es significativa en los parámetros de estimación a diferencia del nivel de empleo que presenta una diferencia importante para mejorar la producción en el período de poscrisis. Al respecto, Jiménez (2018) al estudiar el producto de largo plazo y su brecha desde dos enfoques distintos, tuvo como resultados que las políticas aplicadas a la demanda afectan a la capacidad de la economía en el largo plazo. Según sus estimaciones del modelo de Solow señala que la demanda no tiene efecto sobre el producto de largo plazo y que sólo influye en las fluctuaciones. Por otro lado Céspedes (2014) señala que el producto potencial peruano depende de determinantes estructurales y de coyuntura que contribuyen en el efecto de largo plazo en el crecimiento del producto. El producto potencial ha experimentado un importante quiebre estructural debido a la crisis internacional de 2008 y 2009, lo que para años posteriores a 2010 presenta un comportamiento decreciente debido a disminuciones importantes de la inversión que a su vez disminuyó la acumulación de capital. Por otro lado, el crecimiento de la productividad la misma que afecta el uso eficiente de los factores de producción, también sería el causante de la reducción del producto potencial peruano. La reducción del PBI potencial peruano tras la crisis fue decreciente y sus importantes determinantes como son la inversión, el empleo y la productividad presentaron el mismo comportamiento. Luego, señala que para recuperar el crecimiento del producto de largo plazo en el Perú es necesario estimular reformas estructurales que incrementen el crecimiento de la inversión y la productividad.
Por otra parte, en el análisis del modelo de Solow considerando el período de pandemia COVID-19 se muestra que no hubo una diferencia significativa en los parámetros estimados a pesar de las medidas de aislamiento social obligatorias implementadas por el Gobierno para salvaguardar la salud de la población. Estas medidas afectaron negativamente a la producción nacional y al empleo (López, 2021; Vega et al, 2021). Sin embargo, esta caída en el producto fue transitoria pues a la producción no le tomó mucho tiempo en recuperarse (Pomasunco y Miranda, 2021). Se debe tener en cuenta que esta recuperación no fue producto de las fuerzas del mercado, sino al trabajo del Banco Central en el control monetario y su acertada coordinación con el Gobierno en la implementación de diversas medidas de política de apoyo a las micro y mediana empresa para reactivar la economía (Armas y Gondo, 2023).
Conclusiones
En este artículo se realiza una exploración del modelo de Solow-Swam para el Perú evaluado en período de crisis internacional y en presencia de la pandemia COVID-19- Para la estimación se emplea el método de mínimos cuadrados completamente modificados (FMOLS) por sus siglas en inglés. En el análisis comparativo de las estimaciones se observa que el nivel de capital en el período antes de la crisis habría sido menor al período poscrisis. Asimismo, en la estimación con toda la muestra el factor capital no muestra una variación importante respecto a la estimación anterior. Este resultado señala que en el largo plazo el efecto del stock de capital sobre el nivel de producción se mantiene sin mucha variación. Por su parte, los parámetros del nivel de empleo en el período pre y poscrisis internacional se ven con una notable variación. Esto indica que el empleo fue un determinante con mayor importancia para mejorar la producción en el período poscrisis lo que es coherente con el hecho que la crisis internacional habría afectado al empleo y esta variable se hizo más importante para incrementar el nivel de producción. La estimación de la muestra completa señala que estos parámetros se habrían mantenido con un comportamiento estable y que la crisis no habría afectado drásticamente en los valores de largo plazo de los parámetros del modelo.
Por otra parte, en el análisis con la presencia de la pandemia COVID-19 se realizaron estimaciones para el período 2001m5-2020m2 y 200Im5-2022ml2 que corresponden al período pre y durante la pandemia. En los resultados no se observa una diferencia significativa en los parámetros de estimación ya que estos presentan valores muy similares a pesar de que las medidas implementadas en el país fueron las más rígidas del mundo donde se paralizó la producción y el empleo; sin embargo, el nivel de producción se habría recuperado inmediatamente. Cabe señalar que el Gobierno tuvo un papel importante en esta recuperación debido que en coordinación con el Banco Central (BCRP) implementaron diversas medidas para reactivar la economía y apoyar a la micro y mediana empresa, como es el caso de la creación del programa REACTIVA-Perú que consistía en la estimulación del crédito a las empresas peruanas para que pudieran seguir operando y disminuyeran su reducción abrupta del empleo. Por otra parte, es claro que la estabilidad que el país fue conservando en la última década fue determinante para hacerle frente a la presencia de la pandemia.
Según esta comparativa de la estimación y los valores de los parámetros, se tiene que los efectos después de la crisis financiera de 2008 habrían tenido mayor impacto en la economía peruana en comparación con la presencia de la pandemia COVID-19- Este fenómeno se debería a que el país, períodos antes de la pandemia, se encontraba con una estabilidad monetaria y fiscal para hacerle frente. En este sentido, las políticas económicas deben de imitarse de aquellas que se implementaron en los últimos años pues fueron capaces de resistir a una pandemia mundial y una rápida recuperación en la producción con el uso de una oportuna coordinación entre el Gobierno y el BCRP.
Agradecimientos
El autor agradece a la Universidad Autónoma de lea (UAI) por el financiamiento del presente estudio. Agradece también al Dr. Giorgio Aquije, a la escuela de Contabilidad, al Departamento de Investigación de la UAI por las facilidades brindadas y a los revisores anónimos de la presente revista por sus contribuciones para mejorar el trabajo.
Referencias
ADEX. (2020). MYPES ayudarán a reactivar el país a través de compras públicas. Recuperado de https://www.adexperu.org.pe/notadeprensa/mypes-ayudaran-a-reactivar-el-pais-a-traves-de-compras-publicas/ [ Links ]
Armas, A., y Gondo, R. (2023). Transición del control de agregados monetarios al esquema de metas explícitas de inflación. Revista Moneda. Recuperado de https://www.bcrp.gob.pe/publicaciones/revista-moneda/revista-moneda-192.html [ Links ]
Barossi-Filho, M., Silva, R G., y Diniz, E. (2005). The Empirics of the Solow Growth Model: Long-Term Evidence. Journal of Applied Economics, 5(1), 31-51. https://doi.org/10.1080/15l40326.2005.12040617 [ Links ]
BCRP. (2022). Base de datos de estadísticas del Banco Central de Reserva del Perú. Recuperado de https://estadísticas.bcrp.gob.pe/estadisticas/series/Links ] Arial, Helvetica, sans-serif" size="2">
Boyko, A. A., Kukartsev, V. V., Tynchenko, V. S., Korpacheva, L. N., Dzhioeva, N. N., Rozhkova, A. V., y Aponasenko, S. V. (2020). Using linear regression with the least squares method to determine the parameters of the Solow model. Journal ofPhysics: Conference Series, 1582(1), 0-8. https://doi.org/10.1088/1742-6596/1582/1/012016 [ Links ]
Céspedes, N. (2014). El producto potencial de la economía peruana. Moneda, 163(5), 2125- Recuperado de http://www.bcrp.gob.pe/docs/Publicaciones/Revista-Moneda/moneda-163/moneda-163-05.pdf [ Links ]
Dickey, D. A., y Fuller, W. A. (1979). Distribution of the Estimators for Autoregressive Time Series With a Unit Root. Journal of the American Statistical Association, 74(366), 427431. https://doi.org/10.2307/2286348 [ Links ]
Gamero, J., y Pérez, J. (2020). Impacto de la COVID-19 en el empleo y los ingresos en Perú (Nota técnica país). Organización Internacional del Trabajo: Panorama laboral en tiempos de la COVID- 19 (Vol. I). Recuperado de https://www.ilo.org/wcmsp5/groups/public/---americas/---ro-lima/documents/publication/wcms_756474.pdf [ Links ]
Gregory, A. W., y Hansen, B. E. (1996). Tests for cointegration in models with regime andtrendshifts. OxfordBulletinofEconomicsandStatistics, 58(2), 555-560. https://doi.org/10.1111/j.1468-0084.1996.mp58003008.x [ Links ]
Gutiérrez, É., Rendón, J., y Álvarez, R (2004). El crecimiento económico en el modelo de Solow y aplicaciones. Semestre Económico, 7(14), 1529- Recuperado de http://www.redalyc.org/articulo.oa?id=165013658001
Hoeffler, A. (2000). The augmented Solow model and the african grotvth debate (CID Working Paper No. 36). Recuperado de https://core.ac.uk/download/pdf/6720369.pdf [ Links ]
Ibarra, D. (2018). El modelo de crecimiento económico Solow-Swan aplicado a la contaminación y su reciclaje. Revista Mexicana de Ciencias Forestales, 4(15), 7-24. https://doi.org/10.29298/rmcf.v4i15.445 [ Links ]
Inada, K.-I. (1963). On aTwo-Sector Model of Economic and a Growth: Comments Generalization. The Review of Economic Studies, 30(2), 119-127. https://doi.org/doi.org/10.2307/2295809 [ Links ]
Jiménez, F. (2017). Crecimiento y desindustrialización prematura en Perú 1950-2015, un análisis kaldoriano. Economía, 40(80), 155-222. https://doi.org/10.18800/economia.201702.005 [ Links ]
Jiménez, F. (2018). Capacidad productiva, cambio técnico y productividad: estimaciones alternativas del producto de largo plazo (Documento de Trabajo No. 454). Recuperado de http://repositorio.pucp.edu.pe/index/handle/123456789/126783 [ Links ]
Kaldor, N. (1957). A Model of Economic Growth. The Economic Journal, 67(268), 591-624. https://doi.org/10.2307/2227704 [ Links ]
Laurente, L. (2021). Demanda de turismo internacional en tiempos de COVID-19 en la región de Puno-Perú. Economía Coyuntural, 6(1), 49-78. https://doi.org/doi.org/10.5281/zenodo.4657227 [ Links ]
López, R. (2021). Ensayo sobre el COVID-19 en el Perú: Algunas reflexiones en medio de la pandemia. Estudios Económicos, 38(76), 259-278. https://doi.org/10.52292/j.estudecon.2021.2156 [ Links ]
Magnani, R (2013). The Solotv Growth Model tvith Keynesian Involuntary Unemployment (No. 1). CEPII. Recuperado de papers2://publication/uuid/lFDD63E0-00A2-48B3-9007-4EC9B6594AE7 [ Links ]
MINCETUR (2020). Perú: Arribo de visitantes extranjeros a establecimientos de hospedaje, según región. Serie estadística 2003-2019- Recuperado de http://datosturismo.mincetur.gob.pe/ appdatosTurismo/Content3.html [ Links ]
Montoro, C. (2020). El programa Reactiva Perú. Revista Moneda, 182, 2433- Recuperado de https://www.bcrp.gob.pe/docs/Publicaciones/Revista-Moneda/moneda-182/moneda-182-04.pdf [ Links ]
Phillips, P. C, y Perron, P. (1988). Testing for a unit root in time series regression. Biometrika, 75(2), 335-346. https://doi.org/10.1093/biomet/75.2.335 [ Links ]
Pomasunco, D., y Miranda, G. (2021). Reactiva Perú: Operatividad e implementación. Revista Moneda, 186, 33-39. Recuperado de https://www.bcrp.gob.pe/publicaciones/revista-moneda/revista-moneda-186.html [ Links ]
Rosas, E. (2017). Estimación empírica del modelo ampliado de Solow-Swan y la hipótesis de convergencia condicional, 1985-2011. Revista de Economía, 33(87), 69114. Recuperado de https://www.redalyc.org/articulo.oa?id=674070979003 [ Links ]
Shaikh, A. M., y Moudud, J. K. (2004). Measuring capacity utilization in OECD countries: A cointegration method (Working Paper No. 415). Recuperado de www.levyinstitute.org/pubs/wp415.pdf [ Links ]
Solow, R M. (1956). A Contribution to the Theory of Economic Growth. The Quarterly Journal of Economics, 70(1), 6594. https://doi.org/doi.org/10.2307/1884513 [ Links ]
Swan, T. W. (1957). Economic growth and capital accumulation. Economic Record,33(64), 103-108. https://doi.org/10.1111/j.1475-4932.1957.tbO1279.x [ Links ]
Thirlwall, A. P. (1979). The balance ofpayments constraint as an explanation of international growth rate differences. Banca Nazionale Del Lavoro Quarterly Review, 32(128), 4553- Recuperado de https://ideas.repec.org/a/psl/bnlqrr/197901.htmlLinks ] Arial, Helvetica, sans-serif" size="2">
Tsoularis, A. (2021). On Some Important Ordinary Differential Equations of Dynamic Economics. In (Ed.), RecentDevelopments in the Solution of Nonlinear Differential Equations, IntechOpen, 118. https://doi.org/doi.org/10.5772/intechopen.97130Links ] Arial, Helvetica, sans-serif" size="2">
Vega, M., Lahura, E., y Saavedra, E. (2021). Análisis de los picos de las dos olas de la pandemia del COVID-19 en el Perú. Revista Moneda, 186, 5255- Recuperado de https://www.bcrp.gob.pe/publicaciones/revista-moneda/revista-moneda-186.htmlLinks ] Arial, Helvetica, sans-serif" size="2">
Willington, C. (1998). Un análisis empírico del crecimiento económico regional en Argentina (Paper de Discusión No. 14). Argentina. Recuperado de https://www.ieral.org/images_db/noticias_archivos/12-53798661.pdf [ Links ]
Zivot, E., y Andrews, D. W K. (1992). Further Evidence on the Great Crash, the Oil-Price Shock, and the Unit-Root Hypothesis. Journal of Business & Economic Statistics, 10(3), 251270. https://doi.org/10.2307/1391541Links ] Arial, Helvetica, sans-serif" size="2">