ARTÍCULOS ORIGINALES

 

El conjunto de los números y dos formas de entender al número "π"
Set of numbers and two ways to understand "π" number

Bruno E. Vargas Biesuz¹
bvargasb@ulasalle.edu.bo
Instituto de Investigación en Ciencias Económicas y Finacieras,
Universidad La Salle Bolivia

Artículo Recibido: 10-01-2017 Artículo Aceptado: 25-02-2017

 

---

Resumen

Es bastante conocido que el número irracional "pi", de amplia aplicación en las matemáticas, es la razón entre la longitud de una circunferencia y el diámetro que esta genera. Sin embargo hay otra forma de entender a este número, a través del cálculo de la superficie de una parte de la circunferencia y esto se logra con el uso de herramientas del cálculo integral.

El método utilizado para este propósito: es el análitico matemático, y el resultado obtenido es la verificación de la propuesta establecida.

Se pretende por tanto, verificar que la integral de una función, definida en un intervalo determinado, resulta ser el número "pi". Luego de una serie de consideraciones, operaciones matemáticas y cálculos, al final del trabajo se obtiene el resultado esperado.

Por tanto, la superficie de media circunferencia es el número "pi" y, esta es una interpretación alternativa, no aritmética de esta importante constante matemática.

Palabras claves: Conjunto de números, numero irracional, número "", integral definida.

---

Abstract

It is well known that the irrational "pi, of wide application in mathematics, is the ratio between the length of a circumference and the diameter that this generates. However there is another way of understanding this number, this is through the calculation of a part of the circumference and this is done with tools of integral calculus.

The method used for this purpose is the mathematical analysis, and the result obtained is the verification of the established proposal.

It intends to verify that the integral of a function over a given interval, also turns to be "pi" number. Carried out some considerations, mathematical operations and calculations, ay the end of this paper, the expected result is reached.

Therefore, the surface of a half circumference is also the "pi" number, this is an non arithmetic alternative interpretation of this fundamental mathematical constant.

Keywords: Set of numbers, irrational number, "number, definite integral.

---

 

 

Introducción

De una u otra forma, todos utilizamos los números y se tiene una noción intuitiva básica de lo que representan. Por otra parte, los sistemas educativos formales, enseñan cómo manejarlos. Sin embargo, a decir del matemático Michael Spivack "... lo que en realidad los números son, queda más bien en la penumbra y no entendemos lo que son" (Spivak,1986, p.16).

Dejando de lado la preocupación por conceptualizar lo que un número és, quienes se ocupan de su estudio, los matemáticos, para entender sus propiedades, utilizarlos y sacarles provecho en muchas aplicaciones, los han ordenado o clasificado en clases o conjuntos. Por supuesto, para este logro han transcurrido muchos años (siglos) y un prolijo trabajo intelectual.

 

Referentes conceptuales

Los números naturales. Estos se los utiliza básicamente para contar y con ellos, se pueden hacer algunas operaciones aritméticas. Se los identifica con el símbolo N y puede definirse como todos los números que son enteros (sin parte decimal) y positivos, es decir mayores que el número cero (0).

N={ 1, 2, 3,........}

Es evidente que los números naturales tienen muchas limitaciones. Por ejemplo, si solo existiesen estos números, no podría ser posible establecer una idea como la de una temperatura de -10° (menos diez grados).

Para superar estas limitaciones los matemáticos idearon las siguientes clases de números.

Los números enteros. A estos se los define como todos los números enteros, tanto positivos como negativos.

Este conjunto de números se los identifica con el símbolo Z (del alemán "Zahl", numero).

Portanto, Z= {...-3,-2,-1, 0,+1,+2,+3 ...}

Al igual que en el anterior caso, con solo la existencia de los números enteros, no sería posible comprender la existencia de algo como 2,35 unidades monetarias.

Esta nueva limitación, fue superada con la definición de un conjunto de números más amplio, que se obtienen dividiendo un par de números enteros.

Los números racionales. A estos números se los designa por el símbolo Q (del inglés "quotient" o cociente).

Los números racionales son números que pueden expresarse en forma de fracción, por ejemplo , en los que a y b son números enteros, pero además, b debe ser necesariamente diferente de cero. En lenguaje matemático, todo esto se expresa como:

Para establecer si un número es racional, de lo que se trata es que el número pueda ser escrito como fracción irreducible. Pueden darse varios casos, por ejemplo.

Todos estos números decimales, que han sido expresados como fracciones, son números racionales.

Sin embargo existen otros números como v2= 1,414213562. ... cuya parte decimal no tiene ningún patrón de repetición. Este tipo de números, también conocidos como números decimales infinitos no periódicos, que definitivamente no pueden ser expresados como fracciones, nos lleva a otro conjunto numérico.

Los números irracionales. A estos se los designa con el número Q^c es decir, los números irracionales son todos los números que no son racionales.

Estos pueden ser conceptualizados como aquellos números que no se pueden expresar como una razón o fracción de dos números enteros.

Existen muchos números irracionales, algunos de ellos son muy conocidos y extremadamente importantes en distintos ámbitos de las ciencias, por ejemplo el número "e" base de los logaritmos naturales (neperianos) y el muy conocido "π". Los matemáticos, han desarrollado varias pruebas formales que muestran la irracionalidad del número "π".

Lo considerado hasta aquí, ayuda al propósito de este artículo, que es presentar dos formas de entender al número irracional "π", lo cual se mostrará luego de explicar otros dos conjuntos de números.

Los números reales. Como los números naturales y enteros, pueden ser expresados como fracciones, N y Z son de hecho también números racionales. Esta consideración permite establecer que la unión del conjunto de los números racionales y los irracionales, determinan el conjunto de los números reales, simbolizados por R.

Los números complejos. Además de todos los conjuntos de números analizados hasta ahora, existen los llamados números complejos. Estos números simbolizados por C, se caracterizan por ser números compuestos por una parte real y una parte imaginaria. Por ejemplo en su forma binomica: 5 + i es un numero complejo en el que cinco (5) es un número real e "i", es llamada "unidad imaginaria":

El número "π", enfoque geométrico. Los sabios geómetras de la antigüedad, ya se percataron de la existencia de una relación intrínseca o de proporcionalidad entre la longitud de una circunferencia (L) y la longitud del diámetro que esta genera (D).

Al dividir la longitud de una circunferencia, entre la longitud de su diámetro, se obtiene siempre un número fijo o constante; este número no es otro que "π", que se aproxima a la cifra : 3,141592654......

Por ejemplo, si la longitud de una circunferencia es 251 cm. y la longitud del diametro es 80 cm. El cociente de estas magnitudes es π = 3,14

En otro caso, con la longitud de la circunferencia de 188,5 cm y un diametro de 60 cm, el cociente es la misma constante matematica π = 3,14. Existe un teorema matemático que prueba rigurosamente que "π" es un numero irracional, cuya demostracion no es sencilla.

 

El numero "π" desde el enfoque del cálculo integral.

Llamemos a "C" la circunferencia con centro en el origen (0,0) y radio unitario (r = 1).

Esta circunferencia puede ser definida como el conjunto de pares ordenados ( x , y ), tales que x² + y² = 1

En ternimos de la notacion de la teoria de conjuntos:

La ecuacion x² + y² = 1, define una circunferencia con centro en el origen y radio unitario.

A partir de la conocida formula geométrica que permite calcular la superficie o area de una circunferencia:

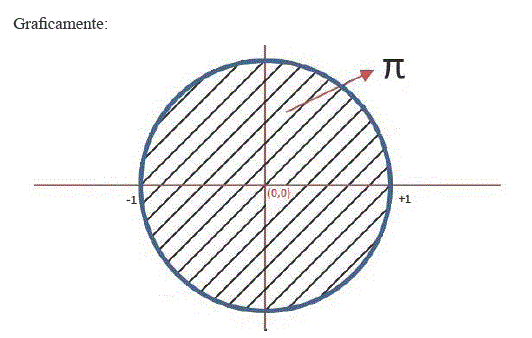
En este caso el area o superficie de la circunferencia "C" es π

Gráficamente:

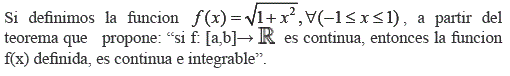
Gráficamente:

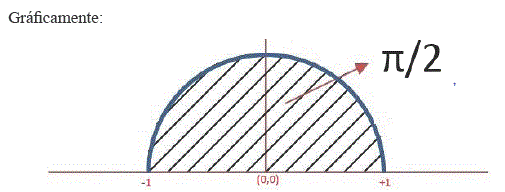
La superficie de esta media circunferencia es π/2. Ahora utilizando la integral de Riemann, como herramienta para calcular la superficie de una figura geometrica, se tiene:

 

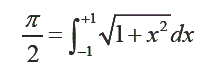
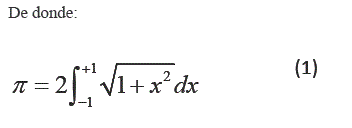
Para verificar esto ultimo, se debe resolver la integral definida dada. Para facilitar el cálculo, expresamos la igualdad (1) del siguiente modo:

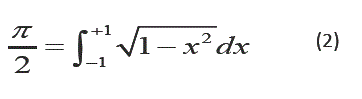
Se resuelve ahora el segundo miembro de la igualdad (2), considerando la siguiente sustitucion trigonometrica:

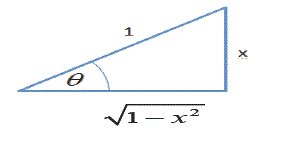
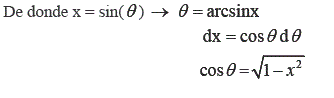
Sustituyendo en (2):

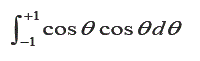
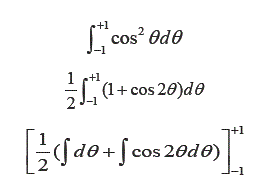
Para resolver el segundo termino de la expresion entre corchetes, se realiza el siguiente cambio de variable:

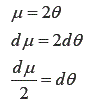
Resolviendo y sustituyendo

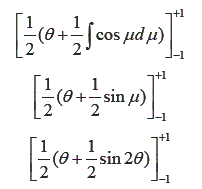
Aquí se debe recordar la siguiente identidad trigonométrica:

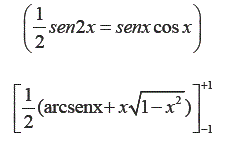
Retomando la ecuacion (2):

 

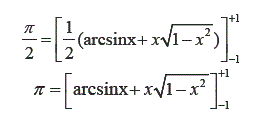
Método

Para probar de forma no aritmética la interpretación del número irracional "π", se utilizó el método analítico matemático, fundamentalmente del cálculo integral.

Resultados y discusión.

Sustituyendo los limites de integración:

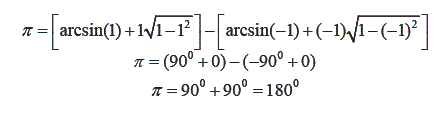
Luego de los cálculos realizados, se verifica que efectivamente, la función integrada, que corresponde a media circunferencia, en el intervalo dado, es el número "pi". Nótese que en la circunferencia trigonométrica definida en radianes, π = 180°, que es precisamente el resultado obtenido.

 

Conclusión.

• Se ha verificado que la constante matemática "pi", no es simplemente la razón entre la longitud de la circunferencia y el diámetro que esta genera, lo cual es una consideración básicamente aritmética. El resultado obtenido, es una forma alternativa de entender al número irracional "pi", mediante el uso de las herramientas del calculo integral. Por tanto, una interpretación matemática alternativa de esta fundamental constante matemática.

• En consecuencia se ha logrado el objetivo establecido y verificado la propuesta.

• Finalmente, es pertinente recordar que esta constante matemática es usada en practicamente todas las ciencias, como ejemplos: toda la geometría de los cuerpos circulares y esféricos; la extensión de sus decimales es útil en el campo computacional; los juegos de las computadoras usan series numéricas con valor "pi"; todos los fenómenos ondulatorios de la física; las ecuaciones de las ondas gravitacionales; las series de Fourrier que se usan en las telecomunicaciones; diseño y fabricación de productos como neumáticos, relojes, vasos, botellas; en astronomía para el cálculo de de la extensión de las superficies de los palnetas, etc.

 

Referencias

Howard E. Taylor & Thomas L. Wade. (1971). Calculo diferencial integral. Mexico: Editorial Limusa Willey.         [ Links ]

Matematicas 7° Primaria.(2001). La Paz Bolivia: Editorial Bruño.         [ Links ]

Spivak, Michael R.(1986). Calculo. Barcelona: Editorial Reverte S.A.         [ Links ]

Smith R. &- Minton R. (2001). Cálculo (Tomo 1). Mc Graw Hill.         [ Links ]

Espinoza Ramos E. (2008) Análisis Matemático I (para estudiantes de ciencias e ingenieria). Servicios Gráficos.         [ Links ]

Lázaro M.(2004) Cálculo Diferencial. Moshera Ed.         [ Links ]