Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Fides et Ratio - Revista de Difusión cultural y científica de la Universidad La Salle en Bolivia
versión On-line ISSN 2071-081X
Fides Et Ratio v.7 n.7 La Paz mar. 2014
ARTICULOS ORIGINALES
VALOR ACTUAL NETO Y TASA DE RETORNO: SU UTILIDAD COMO HERRAMIENTAS PARA EL ANÁLISIS Y
EVALUACIÓN DE PROYECTOS DE INVERSIÓN
NET PRESENT VALUÉ AND INTERNAL RATE OF RETURN: ITS UTILITTAS TOOLS FOR ANÁLISIS AND EVALUATION OF
Lic. Marcos Roberto Mete
Instituto de Investigación en Ciencias Económicas y Financieras Universidad La Salle - Bolivia
marcosmete@gmail.com
Recibido: 07/07/2013
Aceptado: 11/01/2014
RESUMEN
El objetivo del presente trabajo es introducir a los usuarios de las herramientas financieras Valor Actual Neto y Tasa Interna de Retorno en las cuestiones inherentes a su aplicación para la evaluación y selección de proyectos de inversión: utilidad, interpretación de resultados, supuestos implícitos en los cálculos, errores y restricciones. Se presentarán las herramientas Valor Actual Neto modificado y TIR modificada como alternativa para solucionar esos supuestos, errores y restricciones.
PALABRAS CLAVE
Flujos de efectivo, Reinversión, VAN, Valor Actual Neto, Tasa interna de Retorno, TIR, TIR múltiple, TIR modificada, Valor Actual Neto modificado
ABSTRACT
The objetive of this paper is to introduce the users of the Net Present Valué and Internal Rate of
Return financial tools on issues inherent in its application for the evaluation and selection of investment projeets: utility. interpretation of results. assumptions underlying the c al c ul ati o ns , errors and restrictions. Modified VPN and modified TIR tools will be presented as an alternative to solve these assumptions, errors and restrictions.
KEYWORDS
Cashflow, Reinvestment, NPV, Net Present Valué, Internal Rate of return, IRR, Múltiple Internal Rates of return, Modified Internal Rate of return, Modified Net Present Valué.
I. INTRODUCCIÓN
Una vez que hemos confeccionado los flujos de efectivo vinculados con uno o varios proyectos, debemos evaluar la viabilidad económico financiera de las diferentes alternativas que se nos presentan. La decisión pasará por aceptar o rechazar la propuesta en caso de tratarse de proyectos independientes, o bien, de aceptar la más conveniente en caso de tratarse de proyectos mutuamente excluyentes.
La teoría financiera nos brinda una gran gama de herramientas para la evaluación y selección de proyectos, siendo las más utilizadas las basadas en el descuento de flujos de efectivo, Valor Actual Neto (VAN) y Tasa Interna de Retorno/Rendimiento (TIR).
En el presente artículo nos abocaremos al análisis pormenorizado de estas herramientas; veremos sus supuestos, problemas y criterios de aceptación.
Una vez concluido el mencionado análisis presentaremos las alternativas del VAN modificado y TIR modificada como solucionadoras de los problemas y supuestos restrictivos que presentan el VAN y la TIR tradicionales.
El desarrollo del presente artículo se basará tanto en conceptos teóricos como en ejemplos prácticos. Al concluir su lectura, el lector estará en condiciones de comprender las dificultades y problemas que trae aparejada la utilización de las herramientas de VAN y TIR, a la vez que habrá adquirido las competencias necesarias para analizar y aplicar las herramientas VAN modificado y TIR modificada, las cuales resultan imprescindibles para garantizar un correcto análisis financiero en pos de asegurar la estabilidad y proyección futura de las organizaciones.
II. OBJETIVOS
El objetivo general del presente trabajo es adentrar a los usuarios de las herramientas financieras Valor Actual Neto y Tasa Interna de Rendimiento en las cuestiones inherentes a su aplicación para la evaluación y selección de proyectos de inversión: utilidad, interpretación de resultados, supuestos implícitos en los cálculos, errores y restricciones. A su vez, se les presentará como alternativas de solución a esos supuestos, errores y restricciones, las herramientas de Valor Actual Neto Modificado y Tasa Interna de Rendimiento modificada. El objetivo específico consiste en demostrar, a través de un caso de aplicación, como una incorrecta utilización e interpretación de estas herramientas puede conducir a tomar decisiones financieras inapropiadas que pueden poner en peligro la sostenibilidad financiera de las organizaciones.
III. DESARROLLO
l)Valor Actual Neto (VAN)
a) Definición
El Valor Actual Neto de un proyecto es el valor actual/presente de los flujos de efectivo netos de una propuesta, entendiéndose por flujos de efectivo netos la diferencia entre los ingresos periódicos y los egresos periódicos. Para actualizar esos flujos netos se utiliza una tasa de descuento denominada tasa de expectativa o alternativa/oportunidad, que es una medida de la rentabilidad mínima exigida por el proyecto que permite recuperar la inversión, cubrir los costos y obtener beneficios. Para su cálculo se utiliza la siguiente ecuación:
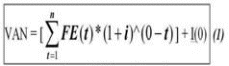
Fuente: Elaboración propia
Donde:
VAN: Valor Actual Neto
FE (t): flujo de efectivo neto del período t
i: tasa de expectativa o alternativa/oportunidad
n: número de períodos de vida útil del proyecto
I (0): inversión inicial (neta de ingresos y otros egresos)
Cabe destacar que el VAN así calculado traduce ingresos y egresos a su valor equivalente en el período 0. Si se quiere seleccionar otro período de referencia, deberá ajustarse la ecuación en la forma correspondiente.
b) Criterio de aceptación
Si el Valor Actual Neto de un proyecto independiente es mayor o igual a 0 el proyecto se acepta, caso contrario se rechaza. Para el caso de proyectos mutuamente excluyentes, donde debo optar por uno u otro, debe elegirse el que presente el VAN mayor.
c) Explicación del criterio de aceptación Un VAN negativo no implica necesariamente que no se estén obteniendo beneficios, sino que evidencia alguna de estas situaciones: que no se están obteniendo beneficios o que estos no alcanzan a cubrir las expectativas del proyecto. Lamentablemente el VAN no nos aclara con precisión en cual de estas situaciones no encontramos, beneficios inexistentes o beneficios insuficientes, solamente nos indica que el proyecto debe rechazarse.
Por lo tanto, un VAN igual a 0 no significa que no haya beneficios sino que ellos apenas alcanzan a cubrir las expectativas del proyecto.
Asimismo, un VAN mayor a 0 indica que el proyecto arroja un beneficio aún después de cubrir las expectativas.
d) Supuestos y consideraciones especiales Los principales supuestos que sustentan y que a la vez limitan el cálculo y la utilización del VAN son los siguientes:
Los ingresos son reinvertidos a una tasa igual a la tasa de expectativa hasta el final del proyecto.
Los egresos tienen un costo financiero igual a la tasa de expectativa.
e) Conclusiones respecto al VAN Los supuestos mencionados precedentemente, restrictivos pero consistentes ya que afectan a todos los proyectos de igual forma, permiten que el VAN sea útil para comparar proyectos mutuamente excluyentes aunque presenten montos de inversión diferentes (escala de inversión) o diferentes patrones de flujos de efectivo, algo que no sucede con la herramienta TIR, de la cual nos ocuparemos más adelante.
En conclusión, podemos afirmar que el Valor Actual Neto, por la consistencia de sus supuestos, es el criterio que debe utilizarse para el análisis y evaluación de proyectos, ya sean independientes o mutuamente excluyentes.
2) Tasa interna de rendimiento/retorno (TIR)
a) Definición
Es otro criterio utilizado para la toma de decisiones sobre los proyectos de inversión y financiamiento. Se define como la tasa de descuento que iguala el valor presente de los ingresos del proyecto con el valor presente de los egresos. Es la tasa de interés que, utilizada en el cálculo del Valor Actual Neto, hace que este sea igual a 0.
El argumento básico que respalda a este método es que señala el rendimiento generado por los fondos invertidos en el proyecto en una sola cifra que resume las condiciones y méritos de aquel. Al no depender de las condiciones que prevalecen en el mercado financiero, se la denomina tasa interna de rendimiento: es la cifra interna o intrínseca del proyecto, es decir, mide el rendimiento del dinero mantenido en el proyecto, y no depende de otra cosa que no sean los flujos de efectivo de aquel.
b) Cálculo de la TIR
El cálculo de la TIR puede resultar muy complejo si la vida útil del proyecto excede los dos períodos. En ese caso, la solución requiere considerar a la TIR como incógnita en la ecuación del Valor Actual Neto, ya que ella tiene la particularidad de ser la única tasa que hace que el resultado de aquel sea igual a 0:
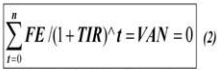
Fuente. Elaboración propia
Donde:
TIR: Tasa Interna de Rendimiento/Retorno
VAN: Valor Actual Neto
FE (t): flujo de efectivo neto del período t
n: número de períodos de vida útil del proyecto
Dado el siguiente flujo de fondos
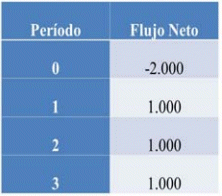
Tabla 1: Flujo de efectivo para V.A.N. y T.I.R.
Los resultados del cálculo del V.A.N son los siguientes:
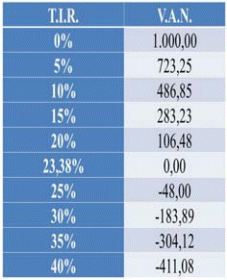
Tabla 2: Resultados del V.A.N.
Tal como puede apreciarse, la tasa que arroja un V.A.N igual a 0 es 23,38%, siendo ella la TI.R del flujo.
Al despejar TIR, la ecuación llega a ser un polinomio de grado T, siendo ella una de las raíces positivas del polinomio.
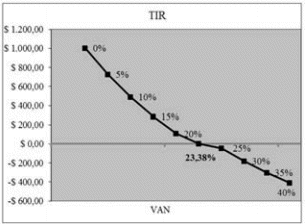
Gráfico 1: V.A.N. y T.LR.
Con T > 2, tal como se mencionara precedentemente, el polinomio se vuelve de difícil solución. En la actualidad, las calculadoras financieras y el software financiero hacen este cálculo en forma rápida.
c) Criterio de aceptación
i. Proyectos independientes: surge de la comparación entre la TIR y la tasa de expectativa o alternativa/oportunidad.
o Si la TIR es mayor a la tasa de expectativa, el proyecto es financieramente atractivo ya que sus ingresos cubren los egresos y generan beneficios adicionales por encima de la expectativa o alternativa.
o Si la TIR es menor a la tasa de expectativa, el proyecto no es financieramente atractivo ya que hay alternativas de inversión que pueden generar mejores resultados. Dentro de este escenario se nos pueden presentar dos alternativas:
o TIR menor a la expectativa pero mayor a 0: significa que los ingresos apenas cubren los egresos del proyecto y no se generan beneficios adicionales.
o TIR menor a 0: significa que los ingresos no alcanzan a cubrir los egresos, por ende, el proyecto genera pérdidas.
o Si la TIR es igual a la tasa de expectativa es indiferente realizar el proyecto o escoger las alternativas, ya que generan idéntico beneficio. En caso de no existir alternativas debería llevarse a cabo el proyecto ya que los ingresos cubren los ingresos y generan beneficios.
¡¡.Proyectos mutuamente excluyentes:
Surge de la comparación entre las TIR de las diferentes alternativas, pero teniendo en cuenta las consideraciones de aceptación/rechazo para proyectos independientes.
o Proyectos de inversión: debe optarse por aquel que presente la mayor TIR. En caso de que ambos presenten TIR negativas, deberían rechazarse y buscar otras alternativas.
o Proyectos de financiamiento: debe optarse por aquel que presente la menor TIR.
d) Supuestos y consideraciones especiales Los principales supuestos que sustentan y que a la vez limitan el cálculo y la utilización de la TIR son los siguientes:
o Los ingresos son reinvertidos a una tasa igual a la TIR hasta el final del proyecto.
o Los egresos tienen un costo financiero igual a la TIR.
e) Problemas, desventajas y limitaciones Una de las mayores desventajas o limitación de la TIR es que su comportamiento depende de la forma y composición de flujo de fondos del proyecto. Existen flujos para los cuales hay una única solución, otros para los que no hay solución posible para la TIR y otros para los cuales hay más de una solución posible.
Otra cuestión a tener en cuenta es que la decisión de aceptar o rechazar proyectos independientes dependerá del tipo de proyecto de que se trate, Inversión o Financiamiento.
Además, en caso de proyectos mutuamente excluyentes, que son aquellos en los cuales solo puede optarse por uno de ellos, la TIR no tiene en cuenta los problemas de diferentes volúmenes de inversión inicial (problema de escala) ni la diferente periodicidad de los flujos de efectivo.
Analizamos cada uno de estos problemas mencionados anteriormente a continuación
i. La TIR múltiple
Si el flujo de fondos presenta un solo cambio en el signo del "flujo neto" tendría una sola TIR. En cambio si el "flujo neto" cambia de signo más de una vez, puede presentarse más de una solución para la TIR. Esta situación se conoce como "TIR múltiple" La razón de esta última situación encuentra su origen en la definición de la TIR: una de las raíces reales positivas del polinomio de grado T que expresa el VAN como función de la tasa de interés. La regla de Descartes plantea que todo polinomio de grado T tiene T raíces, muchas de las cuales coinciden Para el caso de la TIR las raíces son las veces que el "flujo neto" cambia de signo, por ende, un flujo de fondos podría tener tantos resultados de TIR como cambios de signo en el "flujo neto" presente.
Veamos el caso de la TIR múltiple a través de un ejemplo
Dado el siguiente flujo de fondos:
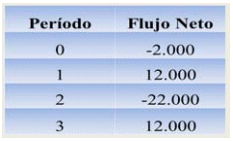
Tabla 3: Flujo Neto que presenta más de un cambio de signo
Tal como puede apreciarse, el flujo neto expone tres cambios de signo, por ende, podrían presentarse hasta tres resultados posibles de TIR.
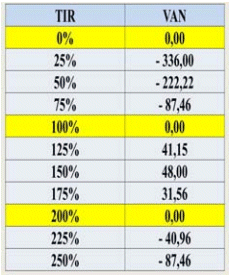
Tabla 4: T.I.R. múltiple
Del cuadro de resultados expuesto anteriormente se desprende que existen tres soluciones posibles de TIR para el flujo en cuestión. La pregunta que surge entonces es: ¿Por qué resultado debo optar? ¿0%, 100%, 200%? Debido que todas carecen de sentido y no existe una buena y justificada razón para optar por una de ellos, la TIR simplemente no puede usarse en este caso.
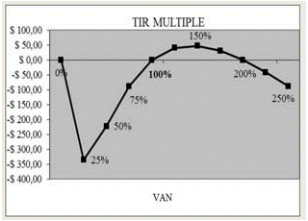
Gráfico 2: T.I.R. múltiple
Tal como se mencionara anteriormente, el criterio de decisión de la TIR para proyectos independientes establece que debe aceptarse un proyecto siempre y cuando su TIR sea mayor o igual a la tasa expectativa. ¿Esto es siempre así o existen casos en los cuales el criterio varíe? Para responder el interrogante veamos el siguiente ejemplo.
Tenemos el proyecto A, de inversión, y su correspondiente flujo:
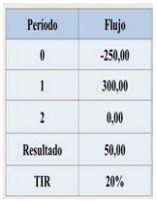
Tabla 5: Ejemplo Proyecto de Inversión
ii.Financiamiento e Inversión
Los proyectos pueden dividirse en dos grandes grupos: aquellos que buscan proporcionar fuentes de financiamiento a las organizaciones (proyectos de financiamiento) y los que proporcionan fuentes de inversión para sus recursos (proyectos de inversión).
En este caso deberíamos aceptar el proyecto si la tasa de expectativa es menor o igual al 20%, caso contrario debería rechazarse.
Ahora nos encontramos frente al proyecto B, de financiamiento, con el siguiente flujo:
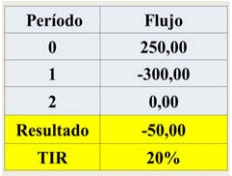
Tabla 6: Ejemplo Proyecto de Financiamiento
En conclusión, tal como puede apreciarse en los ejemplos anteriores, el criterio de decisión de la TIR dependerá del tipo de proyecto de que se trate, inversión o financiamiento. Para el caso de proyectos de inversión el criterio indica que deben aceptarse si la tasa de expectativa es menor o igual que la TIR, mientras que para el caso de proyectos de financiamiento el criterio establece que deben aceptarse siempre y cuando la tasa de expectativa sea mayor o igual a la TIR

Tabla 7: Criterios de Decisión para T.I.R.
iii. Problema de escala en proyectos mutuamente excluyentes
Para analizar este problema me basaré en el planteo de una situación. Se presentan dos propuestas de negocios mutuamente excluyentes. Propuesta 1: usted me entrega 3 bolivianos ahora y yo le devolveré 4,50 el día de mañana. Propuesta 2: usted me entrega 20 bolivianos ahora y yo le devolveré 25 el día de mañana. Usted sólo puede elegir una de las propuestas, ¿cuál de ellas elegiría?
La respuesta correcta es la propuesta 2. Para comprobarlo, basta con analizar el siguiente cuadro resumen.
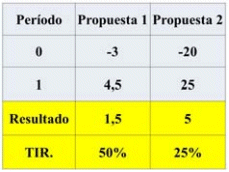
Tabla 8: Ejemplos Propuestas con escalas de inversión diferentes
Este análisis pone en evidencia otro defecto de la TIR. Su regla básica indica que debería optarse por la propuesta 1 porque la TIR es del 50% en comparación con la propuesta 2 que solo alcanza al 25%.
¿En qué esta equivocada la TIR? En que hace caso omiso a los problemas de escala, los diferentes volúmenes de inversión inicial. Aunque la propuesta 1 tiene una TIR mayor, la inversión inicial es mucho más pequeña.
iv. Problema de periodicidad/patrón de los flujos en proyectos mutuamente excluy entes
Al igual que en el caso anterior, para demostrar esta falencia de la TIR, me basaré en un ejemplo.
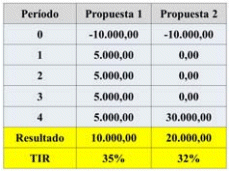
Tabla 9: Ejemplos Propuestas con patrones de flujos de efectivo diferentes
¿Qué propuesta aceptaría usted? La respuesta es la 2, ya que proporciona una ganancia de 20.000 frente a los 10.000 de la propuesta 1.
El interrogante que se plantea es: ¿Por qué conforme a la regla de aceptación de la TIR deberíamos optar por la propuesta 1, con una TIR del 35% y una ganancia de 10.000, en lugar de la propuesta 2 con una TIR del 32% y una ganancia de 20.000?
La respuesta evidencia otra falencia de la TIR., los problemas de periodicidad. Tomando en cuenta que la TIR supone que los ingresos son reinvertidos hasta el final del proyecto a una tasa igual a ella, la propuesta 1 presenta un mayor potencial de reinversión que la propuesta 2 (en esta última no hay posibilidad de reinversión), es por ello que su TIR resulta mayor
f) Conclusiones respecto a la TIR Habiendo desarrollado precedentemente los supuestos restrictivos, problemas, desventajas y limitaciones de la TIR el interrogante a plantear es: ¿por qué, a pesar de todos ellos, se la sigue utilizando en el ámbito financiero?
Es probable que la TIR haya sobrevivido porque resume y presenta la información sobre un proyecto en forma sencilla a través de una sola tasa de rendimiento, algo que el VAN por si solo no permite. Es esa habilidad de la TIR la que explica su supervivencia en el ámbito financiero.
IV. CONCLUSIONES GENERALES Y PROPUESTA DE MEJORA
1) Conclusión Inicial
Luego de la lectura de los puntos precedentes podemos extraer como conclusión que ambas herramientas presentan supuestos y problemas que restringen o, en el peor de los casos, impiden su utilización en el análisis y evaluación de proyectos.
Si bien la TIR resulta la más perjudicada al presentar supuestos y problemas en simultáneo, el criterio del VAN tal como se lo presenta, ve reducida su aplicación debido a los supuestos implícitos en él: reinversión de los ingresos a una tasa igual a la expectativa y egresos con un costo igual a la expectativa, situaciones que muy rara vez se presentan en la realidad cotidiana.
Con el fin de resolver los problemas inherentes en el uso de la TIR y plantear supuestos diferentes en lo que hace a tasa de reinversión para los ingresos y tasa de costo para los egresos, tanto en el uso de la TIR como en el uso del VAN, propongo la utilización de los criterios de Valor Actual Neto Modificado (VANM) y de Tasa Interna de Rendimiento Modificada (TIRM).
2) Propuesta de mejora: VAN y TIR modificados
a) TIR modificada (TIRM)
Con la TIR modificada se garantiza la existencia de una sola tasa, independientemente de la estructura de los flujos, a la vez que se eliminan los problemas de escalas de inversión y patrón de los flujos y se introduce la reinversión de los ingresos y costo de los egresos a tasas diferentes a la TIR.
b) Valor Actual Neto Modificado (VANM)
Con el VAN modificado se eliminan los supuestos implícitos en el VAN tradicional al introducirse la reinversión de los ingresos y costo de los egresos a tasas diferentes a la tasa de expectativa o alternativa/oportunidad.
c) Cálculo del VANM y de la TIRM
El cálculo de ambos se realiza mediante la conversión del flujo neto del/los proyecto/s de la siguiente forma:

Empleando una tasa de interés relevante del mercado financiero ir (tasa de depósitos a Plazo Fijo, inversiones en la Bolsa, compra de moneda extranjera, etc.), se calcula el valor futuro de los ingresos del proyecto en el último período de vida útil (período n). Denominamos a este equivalente VF. Por otro lado se calcula el valor en el período 0 de los egresos del proyecto empleando una tasa de interés relevante del mercado financiero ic (costo de capital: préstamos bancarios, emisión de bonos, etc.); denominamos a ese equivalente VA.
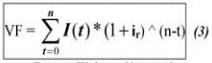
Fuente: Elaboracion propia
Donde:
VF: valor final de los ingresos del proyecto en el último período de vida útil.
I (t): valor de los ingresos del período t.
ir: tasa de interés relevante del mercado para la reinversión de los ingresos del proyecto, n: último período de vida útil del proyecto.

Fuente Elaboracion propia
Donde:
VA: valor de los egresos del proyecto en el período 0.
E (t): valor de los egresos del período t.
ic: tasa de interés relevante del mercado para el cálculo de los costos financieros de los egresos del proyecto n: último período de vida útil del proyecto.
La TiR modificada es aquella que permite establecer una relación de equivalencia entre VA y VF.
![]()
Fuente Elaboracion propia
Así, la TIRM resulta ser el valor positivo de la enésima raíz de la razón entre VF y VA:
![]()
Fuente Elaboracion propia
Para la determinación del Valor Actual Neto Modificado (VANM) procedemos de idéntica manera que para el Valor Actual Neto tradicional: calculamos el neto entre el valor en el período 0 del flujo de ingresos (VF) y el de egresos (VA), utilizando para el cálculo una tasa de interés de expectativa o alternativa/oportunidad i (relevante del mercado financiero)
![]()
Fuente Elaboracion propia
Para el caso de proyectos mutuamente excluyentes que presenten diferentes escalas de inversión debe agregarse la siguiente consideración: los excedentes del inversionista, entendidos como la diferencia positiva entre las inversiones iniciales de ambos, serán reinvertidos a una tasa idéntica a la utilizada para la reinversión de los ingresos ordinarios del proyecto. Una vez calculado el Valor Final de esos excedentes serán sumados al Valor Final de los ingresos ordinarios del proyecto de menor inversión inicial a efectos de determinar su TIR modificada. Donde:
![]()
Fuente: Elaboración propia
VF I = Valor final de la diferencia entre inversiones iniciales de proyectos mutuamente excluyentes
D I (0) = Diferencia entre la mayor inversión inicial y la menor inversión inicial de proyectos mutuamente excluyentes
ir: tasa de interés relevante del mercado para la reinversión de los ingresos del proyecto.
n: último período de vida útil del proyecto.
En este caso la fórmula de la TIRM quedará de la siguiente forma:
![]()
Fueme. Elaboración propia
Para el caso del Valor Actual Neto Modificado (VANM) procedemos de idéntica manera que para el Valor Actual Neto tradicional: calculamos el neto entre el valor en el período 0 del flujo de ingresos (VF) y el de egresos (VA), utilizando para el cálculo una tasa de interés de expectativa o alternativa/oportunidad i (relevante del mercado financiero)
![]()
Fuente: Elaboración propia
d) Criterios de aceptación de la TIRM i) Proyectos independientes: surge de la comparación entre la HRM y la tasa de expectativa o alternativa/oportunidad.
o Si la TIRM es mayor a la tasa de expectativa, el proyecto es financieramente atractivo ya que sus ingresos cubren los egresos y generan beneficios adicionales por encima de la expectativa o alternativa. o Si la TIRM es menor a la tasa de expectativa, el proyecto no es financieramente atractivo ya que hay alternativas de inversión que pueden generar mejores resultados. Dentro de este escenario se nos pueden presentar dos alternativas:
o TIRM menor a la expectativa pero mayor a 0: significa que los ingresos apenas cubren los egresos del proyecto y no se generan beneficios adicionales.
o TIRM menor a 0: significa que los ingresos no alcanzan a cubrir los egresos, por ende, el proyecto genera pérdidas.
o Si la TIRM es igual a la tasa de expectativa es indiferente realizar el proyecto o escoger las alternativas, ya que generan idéntico beneficio. En caso de no existir alternativas debería llevarse a cabo el proyecto ya que los ingresos cubren los ingresos y generan beneficios.
ii) Proyectos mutuamente excluyentes: surge de la comparación entre las TIRM de las diferentes alternativas, pero teniendo en cuenta las consideraciones de aceptación/rechazo para proyectos independientes.
o Proyectos de inversión: debe optarse por aquel que presente la mayor TIRM. En caso de que ambos presenten TIRM negativas, deberían rechazarse y buscar otras alternativas. o Proyectos de financiamiento: debe optarse por aquel que presente la menor TIRM.
e) Criterios de aceptación del VANM i) Proyectos independientes: Si el Valor Actual Neto Modificado (VANM) de un proyecto independiente es mayor o igual a 0 el proyecto se acepta, caso contrario se rechaza.
ii) Proyectos mutuamente excluyentes: debe elegirse el que presente el VANM mayor.
iii) Explicación del criterio de aceptación: Un VANM negativo no implica necesariamente que no se estén obteniendo beneficios, sino que evidencia alguna de estas situaciones: que no se están obteniendo beneficios o que estos no alcanzan a cubrir las expectativas del proyecto. Lamentablemente el VANM no nos aclara con precisión en cual de estas situaciones no encontramos, beneficios inexistentes o beneficios insuficientes, solamente nos indica que el proyecto debe rechazarse. Por lo tanto, un VANM igual a 0 no significa que no haya beneficios sino que ellos apenas alcanzan a cubrir las expectativas del proyecto. Asimismo, un VANM mayor a 0 indica que el proyecto arroja un beneficio aún después de cubrir las expectativas.
3) Ejemplificación de la mejora: VAN y TIR modificados
Proyectos independientes
Dado el siguiente flujo de fondos generado por un proyecto de inversión, cuya tasa de expectativa es del 12% anual
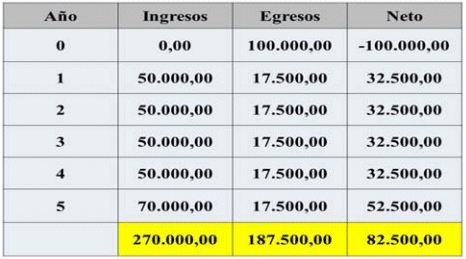
Tabla 10: Flujos de Efectivo del ejemplo de mejora
Los resultados preliminares son los siguientes:
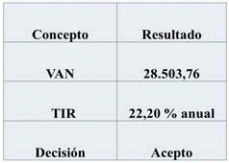
Tabla 11: Resultados preliminares del ejemplo de mejora
Para el cálculo del VAN debe utilizarse la ecuación (1) mientras que para el cálculo de la TIR debe utilizarse la ecuación (2).

(2) TIR = 22,20% anual.
El resultado del VAN asume que los ingresos serán reinvertidos hasta el año 5 a una tasa del 12% anual y que los egresos tienen un costo del 12% anual. Por su parte, el resultado de la TIR asume que los ingresos serán reinvertidos hasta el año 5 a una tasa del 22,20% anual y que los egresos tienen un costo del 22,20% anual. Tal como mencionara precedentemente, estos supuestos rara vez se presentan en la realidad financiera.
A efectos de demostrar las desviaciones que pueden generar los supuestos precedentes tomaremos como referencia una tasa de reinversión para los ingresos del 3% anual y una tasa de costo para los egresos de 10% anual. Los resultados son los siguientes:
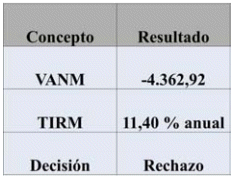
Tabla 12: Resultados ajustados del ejemplo de mejora
Para el cálculo de la TIRM deben utilizarse la ecuaciones (3), (4) y (6), mientras que para el cálculo del VANM deben utilizarse las ecuaciones (3), (4) y (7).

Tal como puede apreciarse, el hecho de haber cambiado los supuestos implícitos del VAN y la TIR en lo que hace a tasas de reinversión y de costo para así calcular el VAN modificado (VANM) y la TIR modificada (TIRM), nos ha llevado a modificar la decisión respecto al proyecto: de aceptar con una TIR del 22,20% y un VAN de 28.503,76 pasamos a rechazar debido a la existencia de un VAN de -4.362,92 y una TIR del 11,40%. Cabe destacarse que el proyecto se rechaza por no cumplir con las expectativas, un rendimiento del 12%. Esto último debe aclararse siempre ya que es diferente la consideración que debe tenerse a un proyecto que no cumple las expectativas a uno que genera pérdidas; respecto al primero podrían buscarse alternativas que lo mejoren y así quede en condiciones de cubrir las expectativas mientras que el segundo debería rechazarse sin más consideraciones.
4) Conclusiones finales
Una vez analizadas en forma detallada las herramientas VAN y TIR podemos extraer como conclusión que ambas, tal como se las presentan inicialmente, cuentan con supuestos y problemas que restringen o, en el peor de los casos, impiden su utilización en el análisis y evaluación de proyectos. Esta situación puede traer graves problemas financieros a aquellas organizaciones que las utilicen de este modo, sin comprender sus supuestos, problemas y criterios de decisión. Para las organizaciones aceptar proyectos que a primera vista parecen redituables, pero que en realidad ni siquiera cubren sus costos, implica poner en riesgo su situación financiera y, por ende, su proyección futura.
A efectos de solucionar los problemas que inicialmente presentan el VAN y la TIR, hemos introducido los conceptos de VAN modificado y TIR modificada. Mediante su utilización el público usuario podrá analizar y evaluar sus proyectos de inversión y financiamiento, en base a pautas reales y sin temer cometer errores que pueden conducirlos a tomar decisiones incorrectas que pondrían en peligro su situación financiera.
El análisis y evaluación de proyectos necesariamente se ve afectado por riesgo e incertidumbre; si a esta situación le agregamos la utilización de herramientas que presentan supuestos restrictivos y problemas en simultáneo, nos encontramos en un escenario que dista de ser el ideal para tomar decisiones tan controversiales como las de obtención e inversión de dinero. Considero que la aplicación de las herramientas de VAN modificado y TIR modificada le agregan solidez al análisis y evaluación de proyectos de inversión. Debemos tener presente que estos proyectos se nos presentan en todos los ámbitos, además del financiero: administración, marketing, ingenierías, sistemas, etc. y que hoy en día resulta imprescindible efectuar un análisis pormenorizado y lo más exacto posible de la sostenibilidad financiera de las organizaciones, ya sean públicas o privadas, tengan o no fin de lucro. Es en este sentido que debe valorarse la contribución efectuada por estas herramientas, necesarias para un correcto análisis envistas de garantizar la estabilidad y proyección futura de las organizaciones.
V. BIBLIOGRAFÍA
[1] Mokate K. M.(2004), "Evaluación Financiera de Proyectos de Inversión", Segunda Edición, Ed. Alfaomega -Uniandes, Colombia, pp. 138-181. [ Links ]
[2] Van Horne J. C, Wachowicz Jr. John M.(2010), "Fundamentos de Administración Financiera", Decimotercera Edición, Ed. Pearson Educación, México, pp. 323-350. [ Links ]
[3] Ross S. A., Westerfield R.W., Jaffe J. F. (2009), "Finanzas Corporativas", Octava Edición, Ed. Me Graw Hill, México, pp. 151-184. [ Links ]
[4] SapagN., SapagR (1998), Fundamentos de Preparación y Evaluación de Proyectos, Editorial Me Graw Hill, México. [ Links ]













