ARTÍCULO ORIGINAL

FUNDAMENTOS SOBRE CONVERGENCIA EN MODELOS ITERATIVOS PARA SISTEMAS DE ECUACIONES LINEALES

 

 

José Gil Iñiguez

Vicerrector Académico ULS

 

 

---

 

 

Introducción.

Iteración de Jacobi.

Esta fórmula define el proceso de Jacobi o de los desplazamientos simultáneos. Desarrollando (5), obtenemos

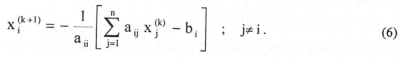
Como se observa, en cada ciclo iterativo se calculan aproximaciones para todas las incógnitas usando solamente aproximaciones del ciclo anterior.

Iteración de Gauss - Seidel.

Este proceso se denomina también de los desplazamientos sucesivos, ya que haciendo i = 1 en (6), tenemos:

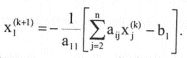
Esta aproximación de x₁ se usa en la aproximación de x₂, o sea:

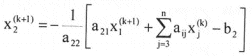
y así sucesivamente, obteniendo en forma general:

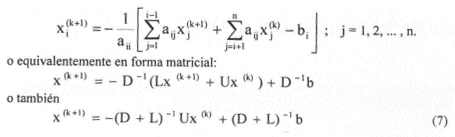
Convergencia.

El criterio anterior de convergencia no podrá ser aplicado bajo la premisa expuesta en el libro "Métodos Numéricos y Programación Fortran" (McCracken y Dom, Ed. Limusa-Wüey, México 1969), donde se asegura queia condición suficiente de convergencia tanto para el método de Jacobi como para el método de Gauss - Seidel es:

La matriz A del sistema es diagonalmente dominante estrictamente, condición más fuerte que la exigida en el libro de McCracken y Dorn. Sin embargo, utilizando el método de Gauss-Seidel tenemos:

Acotación del Error.

Encontraremos ahora una cota superior del error. Si es la diferencia entre dos aproximaciones consecutivas, o sea:

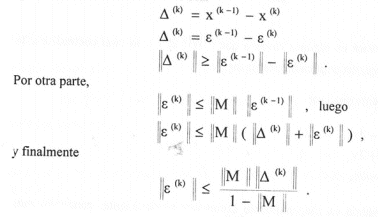
El criterio de convergencia analizado anteriormente no es de mucha utilidad si se lo toma al pie de la letra, ya que son pocos los sistemas de ecuaciones lineales que poseen matrices de coeficientes diagonalmente dominante o matrices de iteración con norma menor que uno; sin embargo si se arreglan las ecuaciones para formar el sistema lo más cercano posible a las condiciones de convergencia anteriormente indicadas, y postulando nuevas condiciones de convergencia como:

Si la sucesión converge a la solución x del sistema, entonces la sucesión de números reales convergerá a cero; si por el contrario esta sucesión de números diverge, entonces puede pensarse que el proceso diverge. Con esta aclaración, un criterio adicional sería detener el proceso una vez que . Por lo tanto, si el proceso iterativo diverge (según los criterios explicados al principio), un despeje adecuado de las incógnitas puede originar convergencia; por ejemplo, en lugar de despejar x_i de la primera ecuación, x₂ de la segunda, etc., se podrían despejar las diferentes x¡ de diferentes ecuaciones, cuidando que los coeficientes de las x_¡ despejadas sean distintos de cero; esta sugerencia presenta, para un sistema de n ecuaciones, n! distintas formas de rearreglar dicho sistema, pero si respetamos lo más que se pueda el criterio de matriz diagonalmente dominante, debemos despejar x, de la ecuación i donde se cumpla que 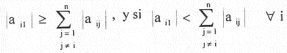, despejar x₁ de la ecuación i donde se verifique que 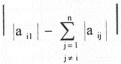tenga el menor valor. Del resto de las ecuaciones hacemos el mismo análisis para x₂ y así sucesivamente podemos encontrar un "buen criterio" para la convergencia si ésta existiera.

Ilustraremos con algunos ejemplos lo mencionado. Como primer ejemplo, veamos el sistema:

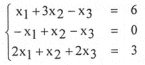
En principio, cualquier método iterativo explicado diverge, pues la matriz del sistema no es diagonalmente dominante y menos estrictamente. Sin embargo, si despejamos x₍ de la segunda ecuación, x₂ de la primera y x₃ de la tercera, tenemos:

Utilizando como aproximación inicial al vector X⁽⁰⁾ = [ 0 0 0 ] ^t y haciendo 18 iteraciones por Gauss - Seidel, obtenemos la siguiente tabla:

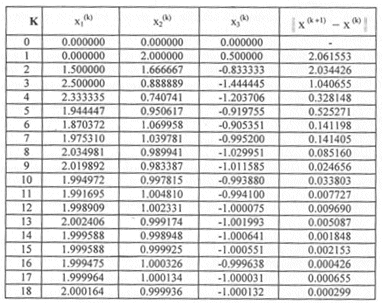
El proceso converge a la solución verdadera, que es:

X = [ 2 1 -1 ]^t

Como un segundo ejemplo, consideremos el sistema

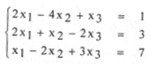
Nuevamente, la matriz del sistema no es diagonalmente dominante. Con el procedimiento explicado, despejamos x₁ de la segunda ecuación, x₂ de la primera ecuación y x₃ de la tercera.

Tenemos entonces el sistema:

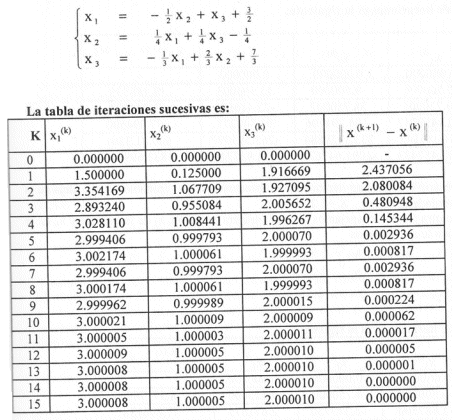
La convergencia a la solución verdadera x = [3 1 2]^t es rápida.

Como tercer ejemplo, consideremos el sistema

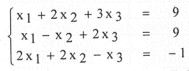
Si despejamos x₁ de la tercera ecuación, x₂ de la segunda y x₃ de la primera, resulta:

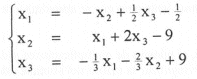
La tabla de iteraciones es la siguiente:

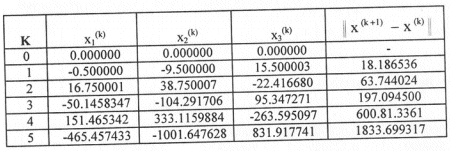
No es necesario realizar más iteraciones: El proceso diverge rápidamente y se aleja de la solución verdadera, que es X = [ 2 -1 3 ]^t

Ensayando otra forma, despejamos x₁ de la tercera ecuación, x₂ de la primera y x₃ de la segunda, con lo que tenemos

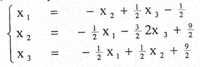
La tabla de iteraciones es la siguiente:

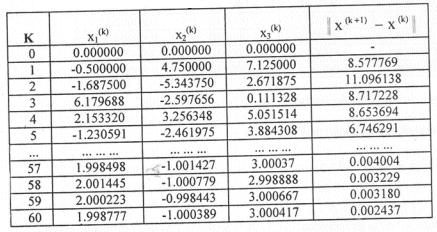
Vemos en este caso que la convergencia es muy lenta pero que se aproxima a la solución verdadera del sistema original.

Para los métodos directos, Gauss - Doolitle, el número de multiplicaciones y divisiones P_n y el número de sumas y restas S_n para triangulizar la matriz del sistema, están dadas por:

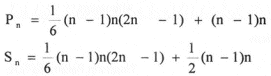
y el número de multiplicaciones y divisiones p_n y el número de sumas y restas s_n para resolver el sistema triangular, están dadas por:

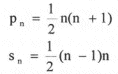
Por tanto, el número total de multiplicaciones y divisiones A y el número total de sumas y restas B son:

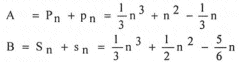
Obviamente, el trabajo computacional para resolver un sistema lineal de orden n por un método directo, es función del número de operaciones necesarias proporcional a n y por otro lado, las necesidades de memoria de máquina serán proporcionales a n^: , lo que constituye mucha exigencia para sistemas que gracias a sus características poseen muchos elementos nulos y por ende son aconsejables los métodos iterativos.

 

Referencia bibliográfica:

- Métodos Numéricos y Programación Fortran

McCraken y Dorn                              Límusa-Wiiey

- Introducción al Análisis Numérico

Anthony Ralston                                Limusa-Wiley

- Análisis Numérico

Gerald                                             Alfaomega

- Análisis Numérico

Burden Richard                                  Alfaomega

- Métodos Numéricos

Burden-Faires                                    Thomson Paraninfo S.A.

- Análisis Numérico

FJ. Scheid                                         McGraw-Hill