Introducción
El acceso irrestricto a la educación de calidad es uno de los derechos humanos más importantes y de mayor amplitud ya que abarca a todas las personas; sin embargo, las brechas educativas entre los grupos de estudiantes son muy evidentes. En ese sentido, el objetivo principal del estudio consiste en determinar el impacto de los años de educación, la desigualdad educativa y el ingreso promedio sobre la inequidad en el ingreso desde el año 1989 hasta el 2019, para lo cual se configura una base de datos de panel para los nueve departamentos de Bolivia. Asimismo, se plantea la hipótesis de que la reducción de la desigualdad educativa y el aumento de los años de educación promedio y del ingreso promedio mensual de Bolivia han impactado significativamente en la disminución de la inequidad en la distribución del ingreso desde el año 1989 al 2019.
Se realiza una regresión lineal por mínimos cuadrados ordinarios (MCO) con datos de panel para los nueve departamentos de Bolivia, en la cual el índice de Gini del ingreso (Gini) es regresado y los años de educación promedio (AEP), el coeficiente de Gini de educación (E) y el ingreso promedio mensual (Ingreso) son los regresores. De acuerdo a los resultados obtenidos, el RA2 se desagrega en dentro (89%) y entre (67%), además, en general (83%), por lo cual el nivel de representación del modelo es elevado, esto implica que un bajo porcentaje del saldo se explica por el término de error y todos los coeficientes estimados son estadísticamente significativos. Por lo tanto, se puede destacar que el índice de Gini del ingreso (Gini) se relaciona positivamente con el coeficiente de Gini de educación (E) y negativamente con los años de educación promedio (AEP) y con el ingreso promedio mensual (Ingreso). También, el signo positivo del coeficiente de Gini de educación (E) indica que cualquier reducción que pueda tener en el tiempo, alcanzaría a provocar una disminución de similar magnitud en el índice de Gini del ingreso (Gini).
El presente estudio está estructurado en base a cinco secciones. En la primera parte se presenta la revisión de la literatura y en el segundo apartado los aspectos metodológicos que guiaron la investigación. Además, en la tercera sección se describe la evolución del índice de Gini del ingreso, de los años de educación, del coeficiente de Gini de educación y del ingreso promedio y en la cuarta parte se presenta el modelo econométrico con datos de panel. Asimismo, en el quinto apartado se muestra los resultados y de manera posterior las conclusiones de la investigación.
1. Revisión de la Literatura
Se considera a las definiciones de inequidad en la distribución del ingreso (Gini), años de educación promedio (AEP), desigualdad educativa (E) e ingreso promedio (Ingreso). Asimismo, se presenta a los métodos de medición de la inequidad en el ingreso y de la desigualdad educativa.
1.1. Definiciones de Inequidad en el Ingreso
Se entiende que la desigualdad en el ingreso es la dispersión en la distribución del ingreso entre la población. Para McKay (2002), “La desigualdad es diferente de la pobreza pero se relaciona a ella. La desigualdad se refiere a las variaciones en los niveles de vida en toda una población. En contraste, la pobreza se enfoca solo en aquellos cuyo nivel de vida cae por debajo de un nivel de umbral apropiado (como una línea de pobreza). Este umbral se puede establecer en términos absolutos (según una norma determinada externamente, como los requisitos de calorías) o en términos relativos (por ejemplo, una fracción del promedio general de vida). La pobreza relativa intuitiva está más estrechamente relacionada con la desigualdad, ya que lo que significa ser pobre refleja las condiciones de vida prevalecientes en toda la población. Pero el grado de desigualdad tendrá implicaciones para ambas concepciones de la pobreza”. También se ve que: “Con respecto a la desigualdad económica, gran parte de la discusión se ha reducido a dos puntos de vista. Uno se ocupa principalmente de la desigualdad de los resultados en las dimensiones materiales del bienestar y puede ser el resultado de circunstancias fuera del control (origen étnico, antecedentes familiares, género, etc.), así como de talento y esfuerzo. Esta visión tiene una perspectiva ex-post u orientada hacia el logro. La segunda visión se refiere a la desigualdad de oportunidades, es decir, se enfoca solo en las circunstancias que están más allá del control de uno, que afectan los resultados potenciales de uno. Esta es una perspectiva ex-ante o potencial de logro.” (United Nations, 2015).
1.1.1. Métodos de Medición de la Inequidad en el Ingreso
1.1.1.1. La Distribución Personal o por Tamaño del Ingreso. Según Todaro y Smith (2015), se trata del indicador más utilizado, el que considera a los ingresos totales que reciben las personas individuales o los hogares. Se cuantifican los ingresos de cada persona, y se ignora el área de residencia y la ocupación laboral (agricultura, manufactura, comercio, servicios). Por lo tanto, se organiza los ingresos personales de manera ascendente y luego se divide la población total en grupos sucesivos, es decir, en quintiles (quintos) o deciles (décimos) según los niveles de ingreso y luego se determina qué proporción del ingreso nacional total recibe cada grupo. Una medida del grado de desigualdad entre los grupos de ingresos altos y bajos en un país es la proporción de Kuznets que relaciona los ingresos recibidos por el 20 por ciento superior y el 40 por ciento inferior. Para tener un mayor desglose de la distribución del tamaño de los ingresos se obtienen los deciles.
1.1.1.2. Distribuciones Funcionales. Es una medida de la distribución funcional o factorial del ingreso, y explica la proporción del ingreso nacional que recibe cada uno de los factores de producción (tierra, trabajo y capital) desde el punto de vista de Todaro y Smith. En lugar de considerar a los individuos como entidades separadas, explica el ingreso de un factor de producción por la contribución que este factor hace a la producción. Con las curvas de oferta y demanda se determinan los precios unitarios de cada factor productivo, cuando estos precios unitarios se multiplican por las cantidades empleadas eficientemente (costo mínimo), se obtiene una medida del pago total para cada factor. La teoría funcional excluye la influencia de las fuerzas no comerciales, como el poder para determinar los precios de los factores, el papel de la negociación salarial colectiva entre empleadores y sindicatos y el poder del monopolista y terrateniente en manipular los precios del capital, la tierra y la producción.
1.1.1.3. El Índice de Bienestar Ahluwalia-Chenery (ACWI). Como señalan Todaro y Smith, este índice se usa para contabilizar la distribución del ingreso, en el que se evalúa la calidad del crecimiento al valorar los aumentos en el ingreso para todos los individuos, pero se asigna un mayor peso a las ganancias de ingresos de las personas de bajos ingresos.
1.1.1.4. Curva de Lorenz. A partir de los ingresos personales se puede construir la curva de Lorenz de acuerdo a Todaro y Smith, en la que los números de los receptores de ingresos se representan en el eje horizontal en porcentajes acumulativos; por ejemplo, en el punto 20, se tiene el 20 por ciento más bajo de la población (más pobre), en el punto 60, está el 60 por ciento inferior. El eje vertical muestra la proporción del ingreso total recibido por cada porcentaje de la población. Como ambos ejes tienen la misma longitud, es acumulativa hasta el 100 por ciento. La figura se encierra en un cuadrado y se dibuja una línea diagonal desde la esquina inferior izquierda (el origen) hasta la esquina superior derecha, por tanto, representa la igualdad perfecta. En cada punto de esa diagonal, el porcentaje de los ingresos recibidos es exactamente igual al porcentaje de los receptores de ingresos; por ejemplo, el punto en la mitad de la diagonal representa el 50 por ciento de los ingresos que se distribuyen a exactamente el 50 por ciento de la población. En la curva de Lorenz se advierte la relación cuantitativa real entre el porcentaje de receptores de ingresos y el porcentaje de los ingresos totales que han recibido en un período determinado. Ahora, cuanto más se aleja la curva de Lorenz de la diagonal, mayor es el grado de desigualdad representado; el caso extremo de perfecta desigualdad estaría representado por la congruencia de la curva de Lorenz con los ejes horizontales inferiores y verticales de la derecha.
1.1.1.5. Índice de Gini. El coeficiente de Gini (relación de concentración de Gini) es una medida resumida final del grado relativo de desigualdad de ingresos en un país, y se la obtiene al calcular la relación del área entre la diagonal y la curva de Lorenz dividida por el área total de la mitad del cuadrado en el que se encuentra la curva. Por lo tanto, el coeficiente de Gini mide la desigualdad agregada y varía desde 0 (igualdad perfecta) a 1 (desigualdad perfecta). En países con distribuciones de ingresos altamente desiguales, el índice de Gini se encuentra entre 0,50 y 0,70, mientras que en países con distribuciones relativamente iguales es de 0,20 a 0,35. Cuando una curva de Lorenz se encuentra por encima de otra curva de Lorenz, la economía correspondiente a la curva de Lorenz superior es más equitativa que la de la curva inferior; pero cuando se cruzan dos curvas de Lorenz, se establece que es necesaria más información (o supuestos adicionales) antes de determinar cuál de las economías es más igual. Por otro lado, el índice de Gini satisface cuatro propiedades: el anonimato, la independencia de escala, la independencia de la población y el principio de transferencia. El principio de anonimato significa que la medida de inequidad no depende de quién tiene el ingreso más alto. El principio de independencia de escala considera que la medida de desigualdad no es afectada por el tamaño de la economía o de la forma en que se mide los ingresos. El principio de independencia de la población determina que la medida de la inequidad no se basa en el número de receptores de ingresos. Finalmente, el principio de transferencia (principio de Pigou-Dalton) establece que, de mantenerse los ingresos constantes, si se transfiere ingresos de una persona más rica a una persona más pobre, la nueva distribución de ingresos resultante es más equitativa (Todaro y Smith, 2015).
1.2. Definiciones de Años de Educación Promedio
De acuerdo al INE (2021), se considera a los años promedio de escolaridad en analogía a los años de educación promedio y se la define de la siguiente forma: “Número promedio de años de educación formal (nivel básico -inicial, primario y secundario superior universitario -licenciatura, técnico universitario- y superior no universitario -institutos normales superiores, académicos militares y policiales e institutos técnicos) adquiridos por la población de 19 años o más de edad”.
Según el Centro de Población de Minnesota (2015), los Años de Estudio Aprobados se definen así: “Se refiere al número total de años de estudio que haya aprobado efectivamente en la enseñanza formal, una persona de 5 años o más”.
1.3. Definiciones de Desigualdad Educativa
Para Muñoz (2003), la desigualdad educativa sucede cuando la sociedad falla en la logro de igualar las oportunidades de ingreso al sistema educativo a las personas con las mismas habilidades, igualar esas mismas oportunidades entre personas de diferentes estratos socioeconómicos, igualar los resultados de los estudiantes que dediquen a su educación el mismo tiempo y esfuerzo sin que en ello afecte su origen social y promover la adquisición de habilidades para el aprendizaje entre la población con estrategias diferenciadas que logren asemejar el desempeño de los beneficiarios. Para Subirats, Gomá y Brugué (2005), la desigualdad educativa es la exclusión de algunas personas o colectivos sociales del acceso, permanencia y aprovechamiento del sistema educativo.
1.3.1. Métodos de Medición de la Desigualdad de Educación
El coeficiente de Gini de educación es utilizado para determinar el grado de la desigualdad en la educación, es decir, mide el ratio de la media (promedio de años de escolaridad) de la mitad de las desviaciones de escolaridad promedio entre todos los pares posibles de personas, y deriva del índice de Gini que es empleado para medir la distribución del ingreso, la riqueza y la tierra. Conjuntamente, el coeficiente de Gini de educación se puede calcular con datos de matriculación de los estudiantes, inversión en educación o logros educativos.
En el estudio de Maas y Criel (1982)), se estiman los coeficientes de Gini basados en datos de matrícula para diversos países de África Oriental, y encuentran que el grado de desigualdad en las oportunidades educativas varía mucho de un país a otro y que los coeficientes de Gini de matriculación se relacionan negativamente con la tasa de matriculación promedio del país. Siguiendo a Ter Weele (1975), se advierte la estimación de los coeficientes de Gini con datos del financiamiento a la educación para diferentes países de África Oriental. Asimismo, Rosthal (1978) determina el coeficiente de Gini de la educación para Estados Unidos y otros indicadores más para la distribución de la educación estimada. También, Sheret (1988) calcula el coeficiente de Gini para Papua Nueva Guinea en base a las tasas de matriculación. De esa manera, los coeficientes de Gini mencionados anteriormente se determinan en base a las tasas de matriculación o en base al financiamiento de la educación y no sobre la distribución del rendimiento educativo.
El estudio de López, Thomas y Wang (1998) muestra la estimación de los coeficientes de Gini de la educación referentes a 12 países, para lo cual utiliza datos de logros educativos. A continuación, los datos que tenían se actualizan y se amplían a 20 países en una versión posterio (López, Thomas, & Wang, 1999). Igualmente, Thomas, Wang y Fan (2000) calculan el coeficiente de Gini de educación para 85 países en base al logro educativo.
Desde el punto de vista de Thomas, Wang y Fan, la primera ecuación de Gini de la educación para grandes poblaciones es: EL=(1μ)n∑i=2i−1∑j=1pi|yi−yj|pj, donde, E l es Gini de educación basado en la distribución del logro educativo, para grandes poblaciones, μ es el promedio de años de escolaridad de la población, P i y P j representan las proporciones de población con ciertos niveles de escolaridad, y i además de y j son los años de escolaridad en diferentes niveles de logro educativo, n es el número de niveles o categorías en los datos de logros que son siete de acuerdo a Barro y Lee (1993), vale decir, se incluye a sin escolaridad (o alfabetización), primaria parcial, primaria completa, secundaria parcial, secundaria completa, terciaria parcial y terciaria completa.
El valor de Gini de educación es sensible al tamaño de la población N cuando es muy pequeño, esta sensibilidad se refleja con el factor [N/(N-1)]. La segunda ecuación de Gini de educación para una población pequeña es: E=[NN−1]*[(1μ)n∑i=2i−1∑j=1pi|yi−yj|pj]=[NN−1]*EL, dónde, E es la educación Gini basada en la distribución del logro educativo, N es el número de individuos de la población que ha sido considerada.
Si a la primera ecuación se la multiplica por el factor [N/(N-1)], entonces, el resultado sería la segunda función del coeficiente de Gini de educación. Cuando el tamaño de la población N se acerca al infinito, [N/(N-1)]=1, la segunda ecuación se convierte en la primera ecuación. De esta manera, cuando el tamaño de la población es lo suficientemente grande, la primera fórmula es ideal para lograr un alto nivel de precisión (Thomas, Wang y Fan, 2000).
2. Diseño Metodológico del Estudio
En esta sección se identifica el problema de investigación, se plantea la hipótesis y el objetivo del estudio, así como la estrategia metodológica utilizada.
2.1. Problema de Investigación
El problema de la investigación ha sido formulado de la siguiente manera: “Se considera que los años de educación, la desigualdad educativa y el ingreso promedio tienen efectos significativos en la inequidad del ingreso”.
2.2. Hipótesis del Estudio
La hipótesis es la siguiente: “La reducción de la desigualdad educativa y el aumento de los años de educación promedio y del ingreso promedio mensual de Bolivia han impactado significativamente en la disminución de la inequidad en la distribución del ingreso desde el año 1989 al 2019”.
2.3. Objetivo General
El objetivo general de la investigación es: “Determinar el impacto de los años de educación promedio, la desigualdad educativa y el ingreso promedio mensual de Bolivia sobre la inequidad en el ingreso desde el año 1989 hasta el 2019”.
2.4. Alcance Temático, Espacial y Temporal
El estudio se basa en el modelo de Martínez, Hernández y Valles (2015), el cual es parte del enfoque conceptual del desarrollo económico. Se emplea el método del análisis de regresión econométrico a los datos de panel que tiene datos estadísticos de los nueve departamentos de Bolivia y comprende el período 1989-2019.
2.5. Fuentes de Información
Se obtienen datos estadísticos para la variable índice de Gini del ingreso (Gini) y para el coeficiente de Gini de educación (E) con base a la Encuesta de Hogares 1989 al 2019 del Instituto Nacional de Estadística de Bolivia (INE, 2021). Además, la variable años de educación promedio (AEP) y el ingreso promedio (Ingreso) se estima con la Encuesta de Hogares 1989 al 2010, y el período 2011-2019 ha sido complementado con datos de años de educación promedio del INE (2020), y con información del ingreso promedio mensual en la ocupación principal del INE (2021), respectivamente.
2.6. Especificación del Modelo
El modelo econométrico es el siguiente1:
Donde, Gini es la inequidad en la distribución del ingreso, AEP son los años de educación promedio, E denota la desigualdad educativa, Ingreso representa el ingreso promedio mensual de la ocupación principal y μ es el término de error. Además, α es el coeficiente de la pendiente, β 1 , β 2 y β 3 son los coeficientes a ser estimados de los años de estudio promedio, desigualdad en el ingreso e ingreso promedio respectivamente.
3. Evolución del Índice de Gini del Ingreso, de los Años de Educación, del Coeficiente de Gini de Educación y del Ingreso Promedio
En esta parte se describe la evolución del índice de Gini del ingreso, de los años de educación promedio, del coeficiente de Gini de la educación y del ingreso promedio de Bolivia en el período 1989 al 2019.
3.1. Evolución del Índice de Gini del Ingreso
De acuerdo a la Unidad de Análisis de Políticas Sociales y Económicas, UDAPE (2021), la inequidad en el ingreso de los bolivianos ha sido moderadamente oscilatoria y se ha reducido paulatinamente a lo largo del tiempo. Hacia el año 1996, el valor del índice de Gini era de 0,59 y aunque a continuación disminuye levemente, para el año 2005 aumenta a 0,60. Sin embargo, a partir de ese año empieza a descender de tal manera que en el año 2007 era de 0,56 y para el año 2019 continúa disminuyendo de forma notoria hasta el valor de 0,42 (Figura 1).
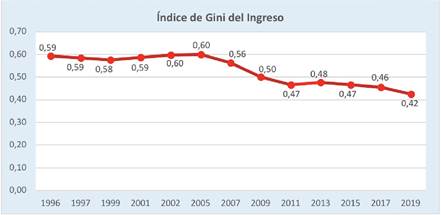
Fuente: Diseño propio en base a la información estadística de UDAPE, 2021.
Figura 1 Bolivia: Índice de Gini del Ingreso, 1996-2019
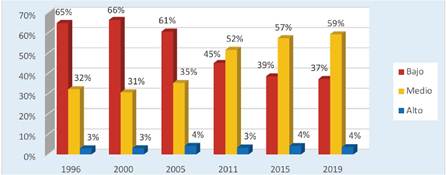
Con base a la información de UDAPE acerca de la distribución de la población según estratos, se ve que desde el año 1996 hasta el 2005 la población de bajos ingresos era la más grande (del 61 al 66%), pero en el período 2011-2019 la población de ingresos medios era la más representativa (del 52 al 59%). La población de ingresos altos crece solamente del 3 al 4 por ciento. (Figura 2)
3.2. Progreso de los Años de Educación Promedio
Según la información estadística del INE (2020), el logro educativo en promedio de la población boliviana se ha incrementado a lo largo del tiempo, aunque no de manera uniforme. Para el año 2011, los años de educación promedio eran de 9,14 y para el siguiente año suben levemente (9,27 años). A continuación, para el año 2013, crecen considerablemente a 9,91 años, pero en el año posterior caen abruptamente (9,37 años). En el período 2016-2019 se incrementan desde 9,35 hasta 9,98 años (Figura 3).
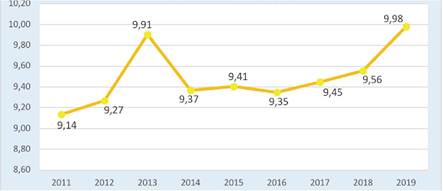
Fuente: Diseño propio en base a la información estadística del INE, 2021.
Figura 3 Años de Educación Promedio, 2011-2019 (En Valores Absolutos)
3.3. Avance del Coeficiente de Gini de Educación
En el largo plazo, el coeficiente de Gini de la educación boliviana se reduce de manera gradual y uniforme. Hacia el año 1989 era de 0,50 y hasta el año 1993 se contrae un poco a 0,48. Conjuntamente, desde el año 1995 al 2007, el coeficiente mantiene el valor de 0,44 y para el período 2009-2015 conserva el valor de 0,42. Posteriormente, en el año 2017 se reduce moderadamente al valor de 0,40 y para el año 2019 alcanza el valor más bajo de todo el período considerado que es de 0,38. Por lo tanto, el coeficiente de Gini de la educación se ha reducido considerablemente a lo largo de los años, lo cual quiere decir que las brechas educativas son más pequeñas (Figura 4).

Fuente: Elaboración propia en base a la Encuesta de Hogares 1989-2019 del INE.
Figura 4 Coeficiente de Gini de Educación, 1989-2019
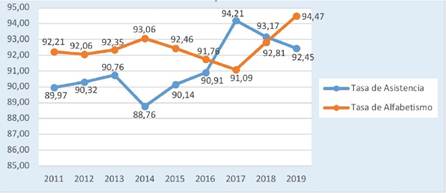
Por otra parte, con base al INE (2020), la tasa de asistencia escolar de la población boliviana entre 6 y 19 años, así como también la tasa de alfabetismo en la población de 15 años o más (INE, 2021) se incrementa moderadamente a lo largo del tiempo pero con oscilaciones considerables. En el año 2011, la tasa de asistencia escolar era del 89,97 por ciento, y para el año 2013 aumenta un poco (90,76%), sin embargo, para el año siguiente se reduce notoriamente a 88,76 por ciento; y hacia el año 2017 se incrementa hasta su máximo nivel (94,21%) y en el año 2019 llega a solamente 92,45 por ciento. Además, la tasa de alfabetismo en el año 2011 era de 92,21 por ciento y en el año 2014 sube levemente a 93,06 por ciento, no obstante, para año 2017 disminuye de manera notoria a 91,09 por ciento, y hacia el año 2019 se incrementa a 94,47 por ciento, el nivel más alto. (Figura 5)
3.4. Evolución del Ingreso Promedio Mensual
El ingreso promedio mensual en la ocupación principal de los bolivianos se incrementa de forma paulatina a lo largo del tiempo (INE, 2020). En el año 2011 era de 1.699 bolivianos y para el año 2013 aumenta a 2.533 bolivianos y en el año 2019 alcanza a 2.967 bolivianos (Figura 6).

Fuente: Elaboración propia en base a la información estadística del INE (2021).
Figura 6 Ingreso Promedio Mensual, 2011-2019 (En Bolivianos)
Ahora bien, con base a las variables presentadas anteriormente, se tiene que analizar el impacto de los años de educación promedio (AEP), el coeficiente de Gini de educación (E) y el ingreso promedio (Ingreso) sobre el índice de Gini del ingreso (Gini).
4. Impacto de los Factores Educativos Sobre la Inequidad en el Ingreso
En esta sección se utilizan datos de panel para Bolivia con la finalidad de determinar el impacto de los años de educación promedio (AEP), el coeficiente de Gini de educación (E) y el ingreso promedio mensual (Ingreso) sobre el índice de Gini del ingreso (Gini) desde el año 1989 al 2019.
4.1. Prueba de Raíz Unitaria a las Variables del Panel de Datos
Como señala Levin, Lin y Chu (2002), se realiza la prueba de raíz unitaria a las variables del índice de Gini del ingreso (Gini), los años de educación promedio (AEP), el coeficiente de Gini de educación (E) y el ingreso promedio mensual (Ingreso), para ello se utiliza los datos estadísticos de los 9 departamentos de Bolivia desde el año 1989 al 2019. Según Hadri (2000), las pruebas de raíz unitaria basadas en panel tienen mayor poder de predicción que las pruebas de raíz unitaria basadas en series de tiempo individuales. Por lo tanto, se plantea las siguientes hipótesis:
| Hipótesis | Estadístico | Decisión |
|---|---|---|
| H 0 :: El panel contiene raíces unitarias, la serie no es estacionaria. | t |
|
| H 1 . El panel no tiene raíces unitarias, la serie es estacionaria. | t |
|
A consecuencia de que todas las variables del panel de datos mostraban una tendencia no lineal e inestable en el tiempo, se las ha linealizado con logaritmos. En cuanto a los resultados de las pruebas de raíz unitaria se observa que la variable Gini resulta ser estacionaria en nivel, sin constante y rezagada un período, es decir, es integrada de orden cero, I(0). Además, la serie de tiempo AEP es estacionaria en nivel y con constante, eso significa que es I(0). También, la variable E es estacionaria en nivel, sin constante y rezagada un período, entonces es I(0). Por último, la serie de tiempo Ingreso resulta ser estacionaria en nivel, sin constante y rezagada un período, eso es, I(0). Entonces, las variables no tienen raíces unitarias, así se rechaza a H 0 ya que la probabilidad del estadístico t es menor que el nivel de significancia del 0,05 por ciento, esto implica que no se rechaza a H 1 . Como las series son I(0), no es necesario realizar pruebas de cointegración al panel de datos, lo que se hace sólo si las variables tienen raíces unitarias o son I(1). En otras palabras, no hay relaciones a largo plazo entre las variables (Tabla 1).
Tabla 1 Pruebas de Raíz Unitaria a las Variables
| Indice de Gini del Ingreso (Gini) en Nivel Sin Constante y Rezagada un Período | ||
| Estadístico | Valor-p | |
| t Sin Ajustar | -1,9979 | 0,0229 |
| t* Ajustada | -1,9327 | 0,0266 |
| Años de Educación Promedio (AEP) en Nivel y Con Constante | ||
| Estadístico | Valor-p | |
| t Sin Ajustar | -5,6027 | |
| t* Ajustada | -4,7559 | 0,0000 |
| Coeficiente de Gini de Educación (E) en Nivel Sin Constante y Rezagada un Período | ||
| Estadístico | Valor-p | |
| t Sin Ajustar | -2,9988 | 0,0014 |
| t* Ajustada | -2,9047 | 0,0018 |
| Ingreso Promedio Mensual (Ingreso) Sin Constante y Rezagada un Período | ||
| Estadístico | Valor-p | |
| t Sin Ajustar | -3,2237 | 0,0006 |
| t* Ajustada | -3,1162 | 0,0009 |
Fuente: Diseño propio en base al programa Stata 15.
En ese sentido, se procede a realizar el análisis de correlación lineal para identificar si existen relaciones entre las variables de educación e ingreso con la inequidad en el ingreso.
4.2. Análisis de Correlación Lineal
A partir del análisis de correlación se puede advertir la relación que existe entre las variables explicativas con la variable explicada del panel de datos.
Entonces, se puede destacar que el índice de Gini del ingreso (Gini) se relaciona positivamente con el coeficiente de Gini de educación (E), y negativamente con los años de estudio promedio (AEP) y con el ingreso promedio mensual (Ingreso). Además, la variable Gini está fuertemente correlacionada con las variables explicativas (Tabla 2).
Tabla 2 Correlación Lineal
| Gini | AEP | E | Ingreso | |
|---|---|---|---|---|
| Gini | 1,0000 | |||
| AEP | -0,8709 | 1,0000 | ||
| A | 0,8275 | -0,7516 | 1,0000 | |
| Ingreso | -0,8780 | 0,8916 | -0,8403 | 1,0000 |
Fuente: Diseño propio en base a los resultados del programa Stata 15.
Ahora bien, al considerar que existe un alto grado de correlación entre las variables, se tiene que estimar el modelo de efectos fijos (Fixed Effects Model, FEM) y el modelo de efectos aleatorios (Random Effects Model, REM), de manera posterior se debe realizar la prueba de Hausman para identificar cuál de los dos modelos está respaldado por los datos.
4.3. Modelo de Efectos Fijos y Aleatorios de Hausman
En base a la prueba de Hausman se puede elegir entre el modelo de regresión con efectos fijos (FEM) y el modelo de efectos aleatorios (REM). De acuerdo a lo establecido, las hipótesis son:
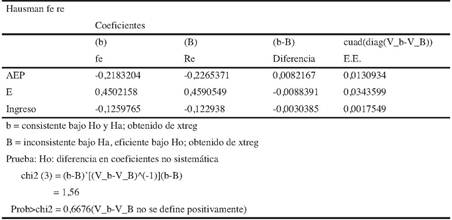
Una vez realizada la prueba de Hausman, se puede establecer que el modelo con efectos aleatorios (REM) es el más apropiado para realizar el análisis de regresión2, por lo tanto, no se rechaza a H0 ya que la probabilidad del estadístico Chi cuadrado es mayor al valor de 0,05 (Tabla 3).
4.4. Regresión Lineal por Mínimos Cuadrados Ordinarios (MCO)
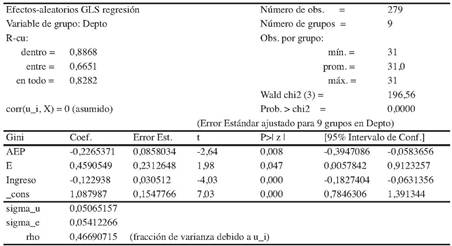
Se realiza una regresión lineal por mínimos cuadrados ordinarios (MCO), en la cual el índice de Gini del ingreso (Gini) es regresado (variable explicada), y los años de educación promedio (AEP), el coeficiente de Gini de educación (E) y el ingreso promedio mensual (Ingreso) son los regresores (variables explicativas). De acuerdo a los resultados obtenidos, el R 2 se desagrega en dentro (89%) y entre (67%), además, en general (83%), por lo cual el nivel de representación del modelo es elevado y todos los coeficientes estimados son estadísticamente significativos3. Por lo tanto, se puede destacar que el índice de Gini del ingreso (Gini) se relaciona positivamente con el coeficiente de Gini de educación (E) y negativamente con los años de educación promedio (AEP) y con el ingreso promedio mensual (Ingreso). También, el signo positivo del coeficiente de Gini de educación (E) indica que cualquier reducción que pueda tener en el tiempo, alcanzaría a provocar una disminución de similar magnitud en el índice de Gini del ingreso (Gini). (Tabla 4)
Tabla 4 Regresión Lineal por Mínimos Cuadrados Ordinarios
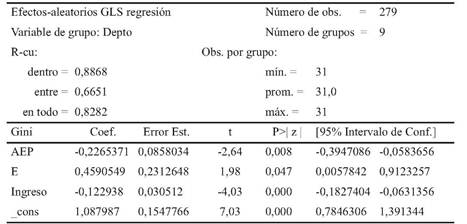
Fuente: Elaboración propia en base a los resultados del programa Stata 15.
A partir de los resultados anteriores se puede ordenar los coeficientes para tener:
Entonces, la ecuación (2) se interpreta de la siguiente forma: si el coeficiente de Gini de educación (E) aumenta en una unidad (y el resto de las variables se mantiene constante), el índice de Gini del ingreso (Gini) se incrementa en 0,45. Asimismo, al considerar que los años de educación promedio (AEP) se incrementan en una unidad, el índice de Gini del ingreso (Gini) se reduce en 0,23 unidades. Además, si aumenta el ingreso promedio mensual (Ingreso) en una unidad, el índice de Gini del ingreso (Gini) se reduce en 0,12 unidades.
Se considera que la desigualdad educativa es el factor de mayor influencia en la inequidad del ingreso, por lo tanto, se proponen una serie de políticas económicas que están orientadas a reducir las brechas educativas entre los grupos de estudiantes.
4.5. Políticas Económicas para Reducir la Desigualdad de la Educación
4.5.1. Políticas Estatales para Disminuir las Brechas Educativas
Uno de los elementos más importantes que crean las brechas educativas en la población es el fracaso escolar, la cual es muy relevante en relación con la exclusión social, no sólo por cuanto se refiere a la marginación o rechazo social e institucional que las personas o colectivos pueden tener a lo largo de su formación (especialmente escolar), sino también, y específicamente, por las funciones que desempeña la educación, es decir, el de otorgar competencias para facilitar la adaptación a la vida profesional y garantizar el desarrollo personal y social que facilite la cohesión y la lucha contra las desigualdades. Además, la dimensión formativa de la exclusión se vincula a otros campos, entre los que destacan el económico y el laboral, esto es, en aquellas áreas en las que se sostiene fundamentalmente la integración social de las personas en las organizaciones y en las comunidades. Ante las diversas formas de exclusiones se necesitan políticas dirigidas a garantizar el acceso al sistema educativo, reducir los niveles de desescolarización, eliminar las barreras e impedimentos al acceso a la educación obligatoria integral, facilitar los medios para la formación de capital humano y social, mejorar y ampliar los programas de alfabetización, reducir el analfabetismo funcional, elevar los niveles formativos bajos con programas de enseñanza, evitar el fracaso escolar con incentivos a los estudiantes, impedir el abandono del sistema educativo con incentivos al estudio y eliminar la barrera lingüística con programas de enseñanza en varios idiomas. (Subirats, Goma, & Brugué, 2005)
4.5.2. Políticas Económicas Integrales Contra la Pobreza y la Desigualdad
En la propuesta de Hujo y Bauerová (2011), se asume que una caída en la tasa de la pobreza no es el resultado de políticas que se concentran en los pobres mediante programas focalizados, sino de políticas que tienen objetivos sociales más amplios como la igualdad, la cohesión social y la justicia social; asimismo, la pobreza está relacionada estrechamente con las desigualdades basadas en la clase social, género, etnicidad y ubicación, que dificultan la inserción de los pobres en los procesos de crecimiento; y por último, no se puede combatir a la pobreza y la desigualdad confiando en que los beneficios del crecimiento económico van a disminuir automáticamente estas problemáticas. Se tienen que aplicar políticas sociales universales, orientadas hacia programas que son económicamente sostenibles, socialmente inclusivos, y democráticamente establecidos; y para lograr el mayor impacto posible, los gobiernos y los actores internacionales implicados en el desarrollo deberían comprometer a las organizaciones (económicas, sociales y políticas) en el diseño de programas considerando que las políticas sociales tienen que ser el eje central. Hay que destacar la necesidad de políticas estatales dinámicas y coherentes que estén orientadas a: 1. La reducción de la pobreza demanda crecimiento y cambio estructural que crea empleos productivos, 2. Los altos niveles de inequidad constituyen un obstáculo para la reducción de la pobreza y deben ser enfrentadas abiertamente, 3. Las políticas sociales amplias son esenciales para la reducción exitosa de la pobreza; 4) La reducción de la pobreza necesita la acción efectiva del Estado y 5. La pobreza se reduce cuando las políticas económicas y sociales, las organizaciones y los convenios políticos se apoyan mutuamente.
4.5.3. Políticas Gubernamentales para la Inclusión al Campo Laboral
Conforme a Subirats, Goma y Brugué, en lo referente al ámbito laboral se pueden distinguir dos tipos de exclusiones sociales, por un lado, la exclusión del mercado de trabajo expresada como las dificultades marcadas de inserción, la exclusión y el desempleo no protegido y de larga duración, y por otro lado la exclusión en el mercado de trabajo, manifestada en la precarización múltiple del empleo y de las relaciones laborales. Aquellas formas de exclusión se focalizan de forma especial y más intensa en ciertos colectivos, definidos en función de sus bajos niveles educativos, de su origen cultural, de su edad, de su contexto familiar y relacional de género, y de su condición de salud. Para evitar la exclusión laboral se puede regular condiciones de estabilidad, establecer condiciones salariales mínimas, dignas y sin excepciones, lograr instrumentos de participación en las empresas, diseñar políticas de bienestar laboral, crear programas de formación permanente, elaborar políticas de educación integral, ofrecer servicios públicos de intermediación y crear nuevas fuentes de empleo. (Brugué, Goma, & Subirats, 2002)
4.5.4. Políticas Públicas de Inclusión en la Vivienda y el Espacio Urbano
Siguiendo a Brugué, Goma y Subirats, en el área de la vivienda y el espacio urbano, la exclusión viene generada por el carácter socialmente selectivo y segregador de los mercados del suelo y de las inmobiliarias, lo que implica una presencia pública generalmente débil o residual. Principalmente hay tres tipos de exclusión, en primer lugar, la discriminación en el acceso y la precariedad económica originada por el excesivo gasto en la vivienda, en segundo lugar, la residencia en condiciones de infravivienda (vivienda sin servicios y equipamientos básicos) y hacinamiento, y en tercer lugar, la desigualdad urbana, es decir, la residencia en barrios sujetos a la degradación. Estas formas de exclusión se focalizan de forma especial y más intensa en ciertos colectivos de bajos ingresos, de su origen u opción cultural, de su edad, de su contexto familiar y relacional de género y de sus condiciones de salud. Las políticas que se proponen son las de promoción pública de viviendas de integración social, subvenciones directas a grupos en riesgo de exclusión, la municipalización de suelo, la oferta de viviendas sociales en el mercado secundario (municipal o pública y privada), la intermediación pública y la regulación del mercado de alquileres, la fiscalización de viviendas vacías, un programa de reconversión en alquileres sociales y las políticas urbanas de una ciudad compacta, es decir, los usos, transporte público, equipamientos, espacios de conectividad, dispersión de centralidades y la supresión de barreras arquitectónicas.
5. Resultados de la Investigación
Se realiza una regresión lineal por mínimos cuadrados ordinarios (MCO) con datos de panel para los nueve departamentos de Bolivia, en la cual el índice de Gini del ingreso (Gini) es regresado y los años de educación promedio (AEP), el coeficiente de Gini de educación (E) y el ingreso promedio mensual (Ingreso) son los regresores. De acuerdo a los resultados obtenidos, el RA2 se desagrega en dentro (89%) y entre (67%), además, en general (83%), por lo cual el nivel de representación del modelo es elevado, esto implica que un bajo porcentaje del saldo se explica por el término de error y todos los coeficientes estimados son estadísticamente significativos. Por lo tanto, se puede destacar que el índice de Gini del ingreso (Gini) se relaciona positivamente con el coeficiente de Gini de educación (E) y negativamente con los años de educación promedio (AEP) y con el ingreso promedio mensual (Ingreso). También, el signo positivo del coeficiente de Gini de educación (E) indica que cualquier reducción que pueda tener en el tiempo, alcanzaría a provocar una disminución de similar magnitud en el índice de Gini del ingreso (Gini).
Entonces, la función estimada [ecuación (2)] se interpreta de la siguiente forma: si el coeficiente de Gini de educación (E) aumenta en una unidad (y el resto de las variables se mantiene constante), el índice de Gini del ingreso (Gini) se incrementa en 0,45. Asimismo, al considerar que los años de educación promedio (AEP) se incrementan en una unidad, el índice de Gini del ingreso (Gini) se reduce en 0,23 unidades. Además, si aumenta el ingreso promedio mensual (Ingreso) en una unidad, el índice de Gini del ingreso (Gini) se reduce en 0,12 unidades. De esta manera, los resultados muestran que la desigualdad en la educación (E) es el factor de mayor relevancia que influye en el aumento de la inequidad del ingreso (Gini), lo cual suele encontrarse en poblaciones con altos niveles de pobreza, así como también con elevados niveles iniciales de inequidad en el ingreso y que tienen un patrón de crecimiento distributivo que no favorece a los más necesitados.
Por lo tanto, se valida la hipótesis del estudio porque la reducción de la desigualdad educativa (E) y el aumento de los años de educación promedio (AEP) y del ingreso promedio mensual (Ingreso) de Bolivia han impactado significativamente en la disminución de la inequidad en la distribución del ingreso desde el año 1989 al 2019. No obstante, se debe considerar que, a consecuencia de tener altos niveles de pobreza y elevados niveles iniciales de inequidad en la distribución del ingreso, cualquier efecto positivo en la reducción de las brechas educativas pueden ser muy limitado, además, el impacto de los factores educativos no es muy visible y se presenta en el largo plazo.
En vista de que la desigualdad educativa es el factor de mayor influencia en la inequidad del ingreso, se propone una serie de políticas económicas que están orientadas a reducir las diferencias educativas y la exclusión social. De esa manera, se plantean las políticas estatales para disminuir las brechas educativas, las políticas económicas integrales contra la pobreza y la desigualdad, las políticas gubernamentales para la inclusión al campo laboral y las políticas públicas de inclusión en la vivienda y el espacio urbano. También, se puede advertir que no hay un enfoque único para reducir la desigualdad educativa, la pobreza y la inequidad en la distribución del ingreso, y se necesita de una fuerte intervención estatal en la conducción de la economía.
Conclusiones
1. En Bolivia, la inequidad en el ingreso ha sido moderadamente oscilatoria y se reduce paulatinamente a lo largo del tiempo; hacia el año 1996, el valor del índice de Gini era de 0,59 y aunque a continuación disminuye levemente, para el año 2005 aumenta a 0,60; sin embargo, a partir de ese año empieza a descender de tal manera que en el año 2007 era de 0,56 y para el año 2019 continúa disminuyendo de forma notoria hasta el valor de 0,42. Además, los años de educación promedio se han incrementado a lo largo del tiempo, aunque no de manera uniforme ya que en el año 2011 eran de 9,14 y para el siguiente año suben levemente (9,27 años); a continuación, para el año 2013, crecen considerablemente a 9,91 años, pero en el año posterior caen abruptamente (9,37 años) y en el período 2016-2019 se incrementan desde 9,35 hasta 9,98 años. También, el coeficiente de Gini de la educación se reduce de manera gradual y uniforme, hacia el año 1989 era de 0,50 y hasta el año 1993 se contrae un poco a 0,48; conjuntamente, desde el año 1995 al 2007, el coeficiente mantiene el valor de 0,44 y para el período 2009-2015 conserva el valor de 0,42; posteriormente, en el año 2017 se reduce moderadamente al valor de 0,40 y para el año 2019 alcanza el valor más bajo de todo el período considerado que es de 0,38; por lo tanto, el coeficiente de Gini de la educación se ha reducido considerablemente a lo largo de los años, lo cual quiere decir que las brechas educativas son más pequeñas. Finalmente, el ingreso promedio mensual se incrementa de forma paulatina a lo largo del tiempo; en el año 2011 era de 1.699 bolivianos y para el año 2013 aumenta a 2.533 bolivianos y en el año 2019 alcanza a 2.967 bolivianos.
2. Se realiza una regresión lineal por mínimos cuadrados ordinarios (MCO) con datos de panel para los nueve departamentos de Bolivia, en la cual el índice de Gini del ingreso (Gini) es regresado y los años de educación promedio (AEP), el coeficiente de Gini de educación (E) y el ingreso promedio mensual (Ingreso) son los regresores. De acuerdo a los resultados obtenidos, el R^2 se desagrega en dentro (89%) y entre (67%), además, en general (83%), por lo cual el nivel de representación del modelo es elevado, esto implica que un bajo porcentaje del saldo se explica por el término de error y todos los coeficientes estimados son estadísticamente significativos. Por lo tanto, se puede destacar que el índice de Gini del ingreso (Gini) se relaciona positivamente con el coeficiente de Gini de educación (E) y negativamente con los años de educación promedio (AEP) y con el ingreso promedio mensual (Ingreso). También, el signo positivo del coeficiente de Gini de educación (E) indica que cualquier reducción que pueda tener en el tiempo, alcanzaría a provocar una disminución de similar magnitud en el índice de Gini del ingreso (Gini).
3. De acuerdo a la ecuación estimada se encuentra que si el coeficiente de Gini de educación (E) aumenta en una unidad (y el resto de las variables se mantiene constante), el índice de Gini del ingreso (Gini) se incrementa en 0,45. Asimismo, al considerar que los años de educación promedio (AEP) se incrementan en una unidad, el índice de Gini del ingreso (Gini) se reduce en 0,23 unidades. Además, si aumenta el ingreso promedio mensual (Ingreso) en una unidad, el índice de Gini del ingreso (Gini) se reduce en 0,12 unidades. De esta manera, los resultados muestran que la desigualdad en la educación (E) es el factor de mayor relevancia que influye en el aumento de la inequidad del ingreso (Gini), lo cual suele encontrarse en poblaciones con altos niveles de pobreza, así como también con elevados niveles iniciales de inequidad en el ingreso y que tienen un patrón de crecimiento distributivo que no favorece a los más necesitados.
4. Ahora bien, se debería considerar que, a consecuencia de tener altos niveles de pobreza y elevados niveles iniciales de inequidad en la distribución del ingreso, cualquier efecto positivo en la reducción de las brechas educativas pueden ser muy limitado, además, el impacto de los factores educativos no es muy visible y se presenta en el largo plazo.
5. En vista de que la desigualdad educativa es el factor de mayor influencia en la inequidad del ingreso, se propone una serie de políticas económicas que están orientadas a reducir las diferencias educativas. De esa manera, se plantea las políticas para disminuir las brechas educativas, las que están dirigidas a garantizar el acceso al sistema educativo, reducir los niveles de desescolarización, eliminar las barreras e impedimentos al acceso a la educación obligatoria integral, facilitar los medios para la formación de capital humano y social, mejorar y ampliar los programas de alfabetización, reducir el analfabetismo funcional, elevar los niveles formativos bajos con programas de enseñanza, evitar el fracaso escolar con incentivos a los estudiantes, impedir el abandono del sistema educativo con incentivos al estudio y eliminar la barrera lingüística con programas de enseñanza en varios idiomas. También, se muestra políticas contra la exclusión social, es decir, las políticas contra la pobreza y la desigualdad, las políticas para la inclusión al campo laboral y las políticas públicas de inclusión en la vivienda y el espacio urbano.