ARTÍCULO

 

Identificación de modelos de aproximación de betas financieras en su medición del riesgo-retorno, aplicable al sistema financiero bancario de Bolivia

 

Identification of models of approximation of financial betas in its measurement of the risk-return, applicable to the banking system of Bolivia

 

 

Juana Isabel Vidaurre Ortega

Licenciada en Administración de Empresas. Universidad Católica Boliviana "San Pablo", Unidad Académica Regional de Santa Cruz de la Sierra
juanividaurre@gmail.com

 

 

---

RESUMEN

El presente trabajo de investigación, tiene como objetivo identificar un modelo de aproximación del coeficiente beta en su medición riesgo-retorno, que pueda ser aplicado al Sistema Financiero Bancario de Bolivia. Por lo anterior mencionado, dentro de este estudio, se aborda la conceptualización e importancia del rendimiento y riesgo, su relación, su aproximación a lo largo de más de cinco décadas y cuyas aportaciones de intelectuales han cambiado la dirección de las finanzas. Posterior a la teoría, se realizó la aproximación práctica de los modelos alternativos para la estimación del coeficiente beta, al igual que su relación y correlación con el modelo tradicional. La propuesta consiste en una estimación que tome sus inicios en el criterio del evaluador y se respalde con medidas estadísticas y econométricas a la hora de calificar el riesgo-retorno de un banco.

PALABRAS CLAVE: Sistema financiero, riesgo-retorno, coeficiente beta

CLASIFICACIÓN JEL: G0, G19

---

ABSTRACT

The present paper was made to identify model to approximate the risk measure Beta over the relationship risk-return that can be applied to the financial bank system of Bolivia. Therefore, within the theoretical framework described and values the importance of the performance and risk, their relationship and their approach around a study of more than five decades, by intellectuals whose contributions have changed the direction of corporate financials. Then practice theory approach of alternative models was preformatted traditional beta coefficient, as well as their relationship and correlation with the traditional model. The proposed is an estimate, which stars with the judgment of the evaluator and is supporting within statistics models and econometrics.

KEY WORDS: Financial system, risk-return, coefficient beta

JEL CLASSIFICATION: GO, G19

---

 

 

1. Introducción

Cuando una persona toma la decisión de invertir; ya sea en un proyecto de negocio o en títulos valores, ya cuenta con una idea de cuánto desea ganar, así como del probable rendimiento que se obtendrá.

Por lo tanto, los principios económicos tiene como esencia, que como seres humanos, siempre buscamos satisfacer el interés propio, y lo recalca uno de los pasajes más famosos de Adam Smith "el pan no lo obtenemos en el Mercado por la benevolencia del panadero, ni la carne por la benevolencia del carnicero, sino porque éstos buscan una ganancia monetaria". Por lo tanto, el hecho de invertir capital en una determinada acción o proyecto, tiene por objetivo inmerso el generar ganancias (rentabilidad, rendimiento o retorno).

Si bien la finalidad de una inversión son los retornos esperados, inherente a esta declaración se encuentra el riesgo de posibles pérdidas o rendimientos por debajo de lo esperado, y cuya relación (riesgo-retorno) fue estudiada por Markowitz, con la finalidad de minimizar la exposición del inversionista al riesgo, maximizando mediante la combinación de carteras de inversión; el rendimiento esperado. Desde la publicación de la teoría de Selección de Portafolio, (Portfolio Selection en inglés) de Markowitz, las decisiones de inversión dieron un gran giro, y como resultado de la teoría los agentes económicos empezaron a formalizar sus metodologías de análisis y estructuración de portafolios optimizados.

A lo largo de los más de 60 años que lleva de uso el modelo de Markowitz, se han puesto en práctica diferentes modelos que coadyuven a esta teoría a estimar el rendimiento a esperar de un activo, de ahí nace uno de los modelos de valuación de activos de capital más famosos: El "Capital Asset Pricing Model" (CAPM), propuesto originalmente por Sharpe y Lintner como una extensión natural al modelo de promedio-varianza de Markowitz

En respuesta a los rendimientos esperados de los inversionistas, el modelo del CAPM, asume la perspectiva del inversor diversificado, y está construido sobre la base que el coeficiente Beta es la medida del riesgo apropiada y qué el inversor sólo demanda recompensas por el riesgo de mercado.

Desde la aparición del CAPM, distintos investigadores han realizados numerosos estudios para evaluar el desempeño del CAPM, por lo cual hasta el día de hoy aún se debaten las desventajas dentro los componentes del modelo.

Una de las críticas más transcendentales es la estimación del coeficiente Beta por su inestabilidad a través del tiempo. Todo se resume en una gran cantidad de información dentro de una sola figura y esta fuerza se convierte en su debilidad [VERNIMMEN, 2010]. Es por ello que su cálculo ha generado controversia a la hora de aplicar un modelo que represente lo que lleva inmerso el coeficiente Beta (la sensibilidad de los cambio en el rendimiento de una acción con respecto a los cambios en el rendimiento del mercado).

Dentro del presente trabajo, se dispuso aplicar modelos de análisis del riesgo sistémico (coeficiente Beta), que permitan estimar de manera más realista, la exposición del inversionista al riesgo del mercado, tomando dentro de su estimación, datos numéricos proporcionados por el mercado y perspectivas profesionales acerca de la relación de los movimientos del rendimiento del mercado con los rendimientos esperados de Empresas o títulos valores.

 

2. Problemática

En países desarrollados, con mercados bursátiles ya maduros, profundos y amplios en información, la estimación del coeficiente Beta, no conlleva gran complejidad, pero si, en países emergentes y en vías de desarrollo en los cuales no existe una amplia gama de empresas que cotizan en bolsa, y si las hay, suelen ser oligopolios o muestras no significativas, la estimación del coeficiente Beta no tiene bases profundas. [PEREIRO, 2010, Pág. 110]

Si bien la estimación del binomio riesgo-retorno que el Beta financiero conlleva en sí mismo, una paradoja en su cálculo. ¿Qué soluciones plausibles, utilizan hoy en día, países con mercados emergentes, como Brasil, Argentina, Chile, entre otros? Dentro de los mercados Emergentes, resolver el predicamento de la estimación de Betas para el riesgo de mercado suele ser adquirida, ya sea por cálculo propio, utilización de los servicios Empresas Calificadoras de Riesgo, Betas de países Desarrollados, entre otros que han sido hasta ahora una opción sin precedentes y que hoy en día continúan generando controversias.

En países tales como Argentina, tienen por fuentes de obtención del Beta; la estimación propia dentro de la organización que alcanza a casi el 50% de las empresas que cotizan en bolsa, aun así, se utiliza en un 30% el uso del beta de los Estados Unidos ya sea comparable de una empresa del mismo rubro, o del Beta del sector en su conjunto y solo el 14% de Empresas dentro de la Argentina aplica algún tipo de proceso de corrección de datos de Estados Unidos, para la aproximación eficiente del Beta¹

Por lo ejemplificado anteriormente, Bolivia al ser una economía en vías de desarrollo, no emergente, posee problemas adicionales en la medición del riesgo sistemático, que aparentemente países vecinos como Argentina suelen resolver con mayor audacia. El mercado bursátil boliviano, no es una fuente generadora o captadora de capitales potencialmente desarrollada, ya que cuenta con una cantidad poco significativa de empresas que emiten en bolsa títulos-valores de deuda y de forma esporádica realizan colocaciones de acciones comunes, a pesar de que en la última década su crecimiento es alentador, gracias a las operaciones de titularización².

A pesar del crecimiento del mercado de valores, han sucedido fenómenos controversiales en la economía boliviana como son los constantes cambios en el sistema económico de nuestro país que actualmente ha generado incertidumbre; el cambio disciplinario en la política monetaria, que conllevó a reformar el uso de los instrumentos financieros, incorporando a esto la nueva Ley de Pensiones y la regulación del Estado sobre la exportaciones.

Añadiendo a la inmadurez del mercado bursátil del país, se encuentra la falta de uso de mecanismos de valuación de riesgo, no sólo del riesgo propio que genera la naturaleza de cada empresa, sino también el riesgo sistemático proveniente de la impredecible conflictividad que nos han caracterizado como país en la última década.

Como resultado de la falta de mecanismos de medición de riesgo sistemático, el coeficiente de Beta es un tema de discusión y compleja aproximación en un país con muy poca información. Lo que ha generado, que los rendimientos esperados de los inversionistas dentro del país, estén marcados por tasas que no necesariamente reflejan el riesgo que ellos llegan a asumir.

Considerandos los elementos mencionados anteriormente, el problema de investigación es el siguiente:

¿Los métodos actualmente utilizados para la estimación de Betas permiten una aproximación confiable del riesgo sistemático aplicable al Sistema Económico del Estado Plurinacional de Bolivia?

 

3. Hipótesis

A causa de la inestabilidad de la información que conlleva el cálculo del Beta financiero, este es bastamente criticado por sus resultados y supuestos que manejan, de manera que la hipótesis de esta investigación se formula de la siguiente manera:

"La estimación del coeficiente Beta con valores de mercado puede ser sustituido por métodos alternos aplicable en Empresas financieras bancarias de Bolivia"

 

4. Justificación

La investigación pretende adecuar uno o más mecanismos de aproximación del coeficiente Beta (β) aplicable al sistema financiero bancario comercial de Bolivia, que permitan contrastar la actual aproximación del coeficiente Beta a valores de mercado, en torno a la valoración de Empresas.

 

5. Objetivo general

Identificar un método de aproximación del Beta financiero en su medición del riesgo - retorno aplicable a la economía del Estado Plurinacional de Bolivia.

Objetivos Específicos

• Realizar aproximación para determinar el coeficiente Betas de los diferentes modelos, con las herramientas científicas y/o tecnológicas utilizadas hoy en día, aplicadas a la unidad de análisis.

• Proponer un mecanismo que sea aplicable al sujeto de estudio.

• Determinar los criterios que colaboren a fijar las métricas del modelo del cálculo del Beta Financiero para el caso boliviano.

• Establecer criterios metodológicos de análisis del coeficiente Beta que puedan remplazar la aproximación a valores de mercado.

 

6. Teoría de selección de Cartera

Uno de los aportes más significativos de las finanzas modernas fue creado por Harry Markowitz, un economistas estadounidense, cuyos aportes para la selección eficiente de carteras, le dieron el mérito de recibir el premio nobel de Economía en 1990.

En 1952 Markowitz publicó una teoría titulada Selección de Cartera (Portfolio Selection, por sus siglas en inglés), en el cual estudiaba el proceso de selección de cartera de inversiones.

Dentro de su estudio, Markowitz afirma que la selección de cartera tiene dos etapas principales para los inversionistas: [MARKOWITZ, 1952 pág. 7-69]

• La primera etapa empieza con la observación y experiencia, y termina con la creencia acerca de los rendimientos futuros de las acciones disponibles.

• La segunda etapa inicia con las relevantes creencias acerca de los rendimientos futuros y termina con la elección de un portafolio.

Si bien su trabajo está dirigido a la segunda etapa, este se fundamenta en los siguientes supuestos para formular su teoría;

1. Los accionistas maximizan sus ingresos capitalizando sus ingresos futuros.

2. Los mercados son eficientes y manejan eficientemente la información.

3. Los inversores tienen aversión al riesgo.

4. Los inversionistas tienen en cuenta la rentabilidad esperada de una acción y la varianza de los retornos deseados.

Los inversores prefieren una mayor rentabilidad, a una menor rentabilidad, para un nivel dado de riesgo.

La teoría de Markowitz empieza con la determinación de; el presupuesto del inversionista, diferentes títulos para inversión, y la proporción de inversión en lo anterior.

Modelo de Valuación de Activos de Capital (CAPM)

Para el accionista ha sido de gran soporte la teoría de Markowitz por la eficiencia de elegir carteras de inversión. Pero en una inversión a determinado riesgo, ¿Cuál es la rentabilidad real que debe exigir un inversionista por asumir esa cantidad de riesgo, dado que el mercado le impone el precio del tiempo y el precio del riesgo?

Pues, desde el aporte de la teoría de Selección de Cartera, esta pregunta se ha convertido en la fuente para la creación de modelos que permitan explicar y predecir el comportamiento del Mercado de Capitales.

Por lo tanto, con el objetivo de hacer más aplicable el modelo de Selección de Cartera, Sharpe (1964) y Lintner (1965) proponen formalmente una extensión al modelo de Markowitz, llamada Capital Asset Pricing Model, (CAPM).

El modelo del CAPM, supone que la rentabilidad de un activo debe estar en función lineal y positiva de la covarianza del rendimiento de la acción en relación al rendimiento del mercado (medido por índices bursátiles), y esta covarianza llega a representar la medida del riesgo sistemático, comúnmente representada por el Beta.

Dentro de la función del CAPM, involucra tres elementos para su estimación: primero, la tasa libre de riesgo , que asume que sus rendimientos son seguros y libre de impago. Segundo, se encuentra la prima de riesgo del mercado , entendida como el plus que el mercado debe otorgar al inversionista por elegir un activo con riesgo, y por último se encuentra el ya mencionado, coeficiente de Beta (β), que ajusta la prima por riesgo, acorde a la volatilidad del activo en relación a los movimientos del mercado.

A continuación el Cuadro 1 muestra los componentes que forman parte del modelo del CAPM:

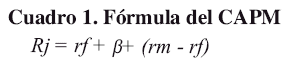
Dónde:

R_j = Rentabilidad esperada de un activo.

r_f = Tasa libre de riesgo.

r_m = Rendimiento del mercado.

β = Riesgo sistemático.

 

Otras aproximaciones para la rentabilidad esperada

Por lo expuesto anteriormente, el modelo del CAPM requiere de la existencia de situaciones o datos, que en la realidad no se presentan a cabalidad y con mayores falencias en los mercados de países emergentes y en vías de desarrollo. A causa de ello es que numerosos profesionales de las finanzas han propuesto cambios o adecuaciones sostenibles teóricamente al simplificado modelo de Share.

A continuación se destacan los modelos que han demostrado mayor consistencia en su hipótesis y resultados en su aplicación empírica.

Betas calculadas con los modelos ARCH-M

El modelo ARCH-M, o también ARCH en la media, es un enfoque presentado por Engle, Lilien, Robins en 1987. Pone la inclusión de la varianza condicional en la ecuación de la media del modelo.

Encuentra su fundamento en la teoría financiera de valuación de activos de la media varianza, según la cual el retorno esperado de un activo está relacionado con su riesgo esperado, y este se mide por su varianza. Esta varianza es llamada incondicional porque asume que la incertidumbre por el rendimiento no varía en el tiempo.

Para generalizar la prima al riesgo, el modelo utiliza la fórmula de ARCH (p, q) que considera a la varianza condicional como un modelo GARCH, de la siguiente manera:

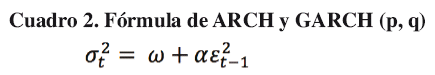
O también

Dónde:

α, ω = Términos constantes siempre positivos.

ε²_t-1 = Variable de interés (termino del error siempre al cuadrado)

Mediante este modelo, primero se verifica si existe volatilidad, es decir, si existe varianza condicional inconstante se procede luego a modelar los errores mediante el modelo ARCH o GARCH (p, q).

Si no fuera el caso y se presenta una varianza condicional constante, se rechaza el uso del modelo ARCH-M y prevalece el coeficiente Beta que se obtuvo mediante la regresión lineal.

Incorporación de Riesgo País

Otra alternativa para estimación de la prima de riesgo es el considerar el riesgo país. El uso de esta herramienta se modernizó desde los años 90's con las empresas calificadoras de riesgo [RIVERO, 2004, Pág. 73-75]

Su estimación está reflejada en el riesgo de crédito de un país Emergente: se toma en cuenta la calificación de riesgo de un Bono del Tesoro General de los Estados Unidos con calificación de riesgo 0 (T-bond) y los bonos emitidos en otro país, la clave de esta cuestión se halla en la posición acreedora o deudora del país que emite dichos bonos.

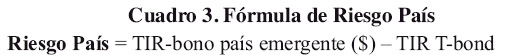
Dumrauf afirma que la suma del riesgo país en el CAPM, es un procedimiento sin prueba empírica cuya estimación se encuentra lejos de ser científico, pero el cual se utiliza mucho, a pesar de presentar los siguientes inconvenientes:[DUMRAUF, 2010, Pág. 254]

• No todas las Empresas sufren de la misma manera el riesgo país.

• Algunos países garantizan el pago de sus deudas manteniendo en su cartera T-Bonds.

• Los fondos analizados en el modelo, usualmente difieren de la duración de flujos de fondos.

 

7. Riesgo de Portafolio o de cartera

Los riesgos que componen un portafolio (entiéndase por portafolio, como la colección de títulos valores de una inversión) son diversos en su forma. Por lo tanto, cuando se habla de un portafolio diversificado de acciones, el riesgo de una acción no debe considerarse únicamente por su riesgo propio (riesgo diversificable), sino también por riesgo no diversificable.

Coeficiente Beta (β)

Si bien, existe un riesgo que es difícil de eludir (riesgo no diversificable), es posible medir el riesgo de mercado de una acción, al observar la tendencia del mismo, a moverse simétricamente con los movimientos generales del mercado, cuya medición es representada por el coeficiente de Beta, el cual se usa ampliamente dentro del modelo CAPM, que conceptualizamos anteriormente.

Los resultados que generan el cálculo de Beta, pueden ser interpretados de la siguiente manera:

• Si el rendimiento de una activo estará muy relacionada a los cambios en el rendimiento del Mercado si el coeficiente de Beta es cercano a 1 (β > 1).

• Los rendimientos de una acción fluctúan simétricamente, con los cambios en el rendimiento del mercado cuando la medición del coeficiente Beta es igual a 1 (β = 1).

• Por el contrario, si el coeficiente de Beta es menor al (β <1) la rentabilidad del activo diverge proporcionalmente de los cambios en los rendimientos del mercado.

Desde la aparición del CAPM, el coeficiente Beta (componente del modelo), ha sido fuertemente criticado por los inconvenientes que presenta su estimación, cuyos resultados del cálculo son muy dependientes de:

1. La cantidad de tiempo sobre el cual es calculado el rendimiento. Ej.: datos diarios, semanales, mensuales o anuales.

2. El número de observación que se tome en cuenta. Ej.: 2 años de rendimientos semanales, 4 años de rendimiento mensuales, etc.

3. El periodo específico usado. Ej.: del 1ro. De Enero al 31 de Diciembre del 2010, o del 1ro. De Enero al 31 de Julio del 2011.

Si bien estos son algunos de los inconvenientes generales de la estimación de Betas, Pereiro remarca que los problemas para estimar el coeficiente de Beta, son aún mayores en Mercados Emergentes:

1. Hay mercados que no tienen las empresas que cotizan en bolsa.

2. Mercados en los que no existe suficiente información nacional o simplemente no es confiable.

3. Suele presentarse precios de acciones con corto tiempo de estimación.

4. Hay mercados que abarca casi en la totalidad de la capitalización de capitales.

5. Frecuentemente los mercados de países Emergentes, suelen mostrar alta volatilidad en sus rendimientos.

En definitiva el modelo inicial del CAPM, genera controversia en su estimación, por lo que a través del tiempo se han presentado diferentes contrastaciones al modelo del CAPM, que a continuación se describe algunas alternativas para la estimación del coeficiente Beta.

 

Otros Métodos para la Estimación del Coeficiente Betas

Betas Comparables

El propósito de este método consiste en buscar una Empresa o conjunto de ellas que contenga similitudes significativas con la Empresa objeto de análisis. Y una vez identificado sus datos se utilizan para el cálculo del costo de capital.

Este método es comúnmente utilizado en países emergentes o en Vías de Desarrollo en cuyos países de origen no existe una secuencia significativa de datos del mercado y normalmente se utiliza como comparables, empresas de mercados bursátiles, donde los movimientos de precio-rendimiento varían con la oferta y demanda. Los datos para su estimación suelen ser brindados por las empresas Calificadoras de Riesgo que brindas datos sobre las Betas y otros índices.

Para utilizar este modelo se debe considerar tres aspectos:

1. El tipo de industria en la que se encuentra la Empresa o Empresas a comparar

2. El grado de apalancamiento operativo tiene parecido razonable

3. El grado de apalancamiento financiero de la Empresa

Una vez seleccionado la Empresa comparable, hay que hacer hincapié en el tercer aspecto; el grado de apalancamiento varía entre Empresas, por lo tanto la estructura de capital nunca es el mismo, en especial en empresas de Mercados Emergentes.

A causa de ese detalle, es que se debe des-apalancar la Beta apalancada de la Empresa a comparar, de la siguiente manera:

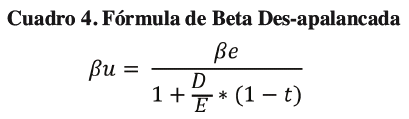
Dónde:

βu= Beta des apalancada

βe= Beta de la comparable

= Relación de endeudamiento de la comparable a precios de mercado

t= Tasa marginal de impuesto a las ganancias de la comparable

Una vez obtenido, se procede a re apalancar el coeficiente de Beta en relación con el endeudamiento de la Empresa local.

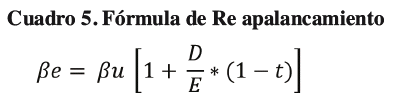
En conclusión, el método de Betas comparables, tiene lógica en su estimación, pero existe el inconveniente de encontrar buenas comparables dentro y fuera del país. No obstante, el uso de este método es uno de los más utilizados por profesores y profesionales a nivel mundial, los cuales aseguran que utilizan este método con respaldo de bases de datos de: Yahoo Finance, Damodaran website, Bloomberg entre otros.

Betas Contables

Una Beta contable se obtiene a través de la comparación de una medida de rendimiento contable de la Empresa y la misma medida de rendimiento contable del mercado. Su teoría tiene base en los estudio realizados por Hill & Stone (1980) donde el Beta calculado con datos contables, puede hallarse mediante la derivada de los retornos sobre el patrimonio de la firma, con respecto a la derivada de los retorno sobre el patrimonio del Mercado. [JIMENEZ, 2012].

Dónde:

β_c = Beta contable basada en el retorno de las acciones (ROE)

Pero, los autores dejan expuesto que las debilidades de un modelo con fuentes contables son las siguientes:

En este tipo de cálculos la estructura de capital tiene una gran influencia en el resultado final, por lo que debe identificarse dicho efecto antes de analizar los resultados.

El uso de rendimientos trimestrales hacen poco robustos los resultados, y requiere de un manejo de pruebas estadísticas constantes.

Se deben tener en cuenta problemas y posibles soluciones para la presencia de auto correlación en la estimación.

Beta Cualitativa

A la fecha, diferentes autores han propuestos alternativas más intrínsecas, para el cálculo del riesgo-retorno y que demuestren la singularidad del riesgo en cada empresa mediante estimaciones cuasi cualitativas y con alto contenido crítico. Dentro de esta investigación se consideran la aproximación cualitativa que analizan los factores internos y externos del riesgo de inversión para cada tipo de empresa.

Dado la ineficiencia de los cálculos de Beta y el escaso significado de las betas históricas, Fernández [FERNÁNDEZ, 2010, Pág. 564] propone una alternativa de estimación del coeficiente Beta, haciendo hincapié en los factores que se consideran riesgosos como parte esencial para estimar la Beta.

La característica principal de este modelo, es de analizar la dinámica de cada uno de los factores que generan riesgo dentro de las actividades de la Empresa, para facilitar la comprensión de los cambios del Mercado con respecto a la Empresa objeto de análisis.

Para la ponderación de los factores está en base al criterio del evaluador como el uso de cualquiera de los métodos. En la estimación, se analiza cada parámetro de riesgo dentro de la empresa, se puntúa del 1 al 5 según su contribución al riesgo, y se define la ponderación de importancia (a mayor riesgo mayor importancia). Terminada la estimación, se procede a sumar las puntuaciones de cada parámetro, y se obtiene la Beta.

Actualmente existen otros métodos cualitativos para la estimación del coeficiente Beta como; CAMEL, MARTILLO y NADEFLEX, entre otros.

Diagnóstico CAMEL

El sistema de calificación CAMEL, se basa en un conjunto de indicadores representativos de la suficiencia de capital, solvencia, y calidad de activos, la calidad de la administración, el nivel y la estabilidad de la rentabilidad y el manejo de la liquidez. Su evaluación es principalmente utilizada en el sector financiero para hacer mediciones de riesgo corporativo y estos componentes en su conjunto logran reflejar la situación de un banco en un momento dado.

Generalmente para llevar a cabo una evaluación tipo CAMEL se requiere la siguiente información:

• Estados Financieros debidamente auditados

• Presupuestos

• Proyecciones de Flujo de Efectivo

• Tablas de amortización de cartera

• Fuentes de financiamiento

• Información relativa a la junta de directores

• Información macro económica.

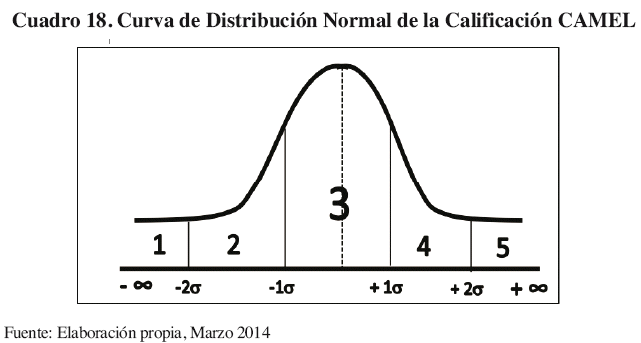
La escala de clasificación se encuentra entre 1 y 5, siendo 1 la calificación óptima indicando fuerte rendimiento y mejores prácticas de gestión del riesgo, mientras que el 5 indica mayor deficiencia, rendimiento débil, y prácticas inadecuadas de la gestión del riesgo.

Para este trabajo de investigación se sigue la metodología de calificación CAMEL enfatizado en la calificación de los ratios financieros. La determinación de escalas para asignar valores entre 1 y 5 se realiza a partir de las desviaciones estándar con respecto a la media de cada componente de calificación del modelo CAMEL.

Como se observa en el Cuadro 8, dada la situación donde el indicador entre "Mayor-Mejor" (por ejemplo los indicadores de rentabilidad), la definición de la escala de calificación 1 se encuentra sumando dos desviaciones estándar para obtener el límite inferior y el "más infinito" se convierte en el límite superior. El caso de que un "Menor-Mejor" valor sea mejor (gastos de administración y gerencia) el proceso se invierte, así el valor de 1 se otorga a los ratios con indicadores que se encuentran entre menos infinito (límite inferior) y la media menos dos desviaciones estándar (límite superior).

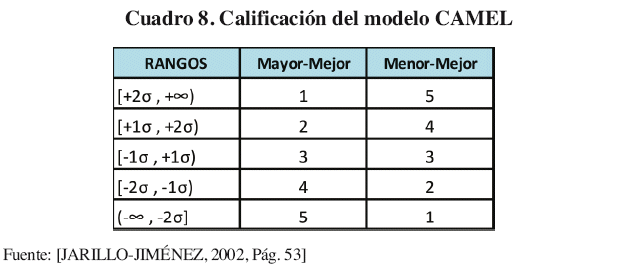
El sistema CAMEL puede ser considerado como una herramienta de filtro, ya que debido a que hay tantas Instituciones Financieras, con frecuencia los reguladores no tienen los recursos para monitorear de cerca cada Institución ya que el sistema CAMEL sólo considera los desempeños históricos y presentes más que los futuros. De manera que se puede errar circunstancialmente a la hora de calificar una institución financiera.

Determinación de la muestra

Para la determinación de la muestra de estudio, la presente investigación determinó como muestra a los Bancos Múltiples [Ley 393 de Servicios Financiero Art. 217] dado que su permanencia en el mercado es la más antigua, además que la complejidad de sus operaciones engloban al resto de las tipologías esgrimidas en la LSF.

Por tanto, los bancos seleccionados son:

• Banco Nacional de Bolivia

• Banco Mercantil Santa Cruz

• Banco Bisa

• Banco de Crédito de Bolivia

• Banco Ganadero

• Banco Económico

 

8. Resultado de la investigación Aproximaciones del coeficiente beta

En el marco de los objetivos, la aplicación práctica de los modelos de estimación del coeficiente Beta descrita con amplitud, es necesaria para la apreciación de sus características, estimación de sus resultados y fiabilidad de los modelos.

Para ello a continuación se realiza las aproximaciones prácticas de los diferentes modelos creados a través del tiempo para la modelación del coeficiente Beta. Se atribuye también los recursos necesarios para la aplicación tanto como sus ventajas y desventajas.

Beta Comparable

Para la aproximación precisa de este modelo se pretende adecuar una Beta del sistema bancario Estadounidense des apalancada, que sirva para re apalancarla con los datos de endeudamiento de los bancos comerciales de Bolivia, a continuación el Cuadro 9, muestra los datos necesarios para la adecuación de este método;

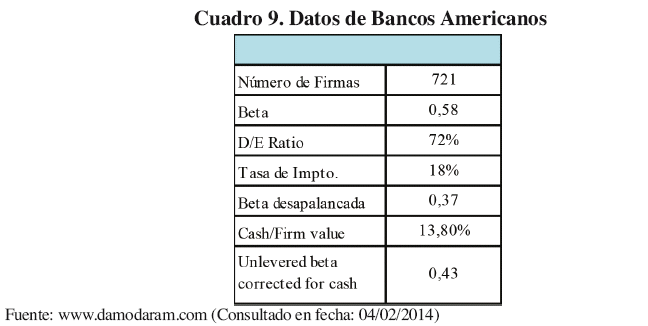
Con los datos anteriores se procede a des apalancar el Beta del sistema bancario estadounidense, lo cual resulta en un Beta de 0,37.

Ahora con la Beta des apalancada y corregida, proporcionamos los datos necesarios del sistema bancario comercial de Bolivia y se procede a re apalancar el coeficiente Beta (ver Cuadro 11.) para cada banco, tomando como fuente de cálculo, su Capital primario³ y Capital secundario todo a valores de mercado.

Particularmente el sistema financiero comercial de Bolivia demuestra una Beta re apalancada de 0,527, ligeramente menor al del sistema financiero estadunidense. El Cuadro 12 muestra el procedimiento de re apalancamiento ejemplificando el sistema financiero bancario comercial.

En la aplicación práctica del modelo para los bancos comerciales, estos fueron comparados de igual manera con el sistema financiero estadounidense. Los coeficientes de riesgo sistemático tienen leves variaciones entre sí. Un coeficiente de 0,51 para el BME demuestra que es el banco con menor relación a los cambios del mercado y en su contra parte el BEC tiene la mayor relación con los cambios en el mercado con 0,61.

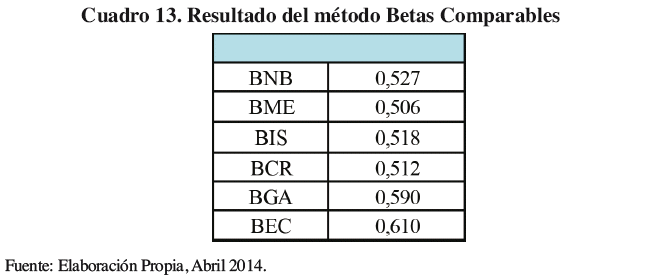
El hecho de tener coeficientes Beta, con proporciones similares al del sistema financiero bancario estadounidense, puede atribuirle el hecho de:

• Irrelevancia del riesgo país que caracteriza a países como el nuestro en Vías de Desarrollo

• Las características diferenciadoras del comparable (productos, servicios, dirección, políticas de dividendos, etc.)

Betas Contables

Para el análisis del coeficiente Beta contable, se recurre a utilizar los Estados Financieros de la empresa a estudiar y el promedio del Sector al que pertenece. En el caso del cálculo del Beta del sistema financiero, se utiliza los rendimientos sobre capital promediados de los bancos comerciales, contra los rendimientos del sistema financiero en su totalidad, lo que resulta en un Beta contable de 0,91 dentro del sistema financiero bancario.

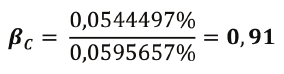
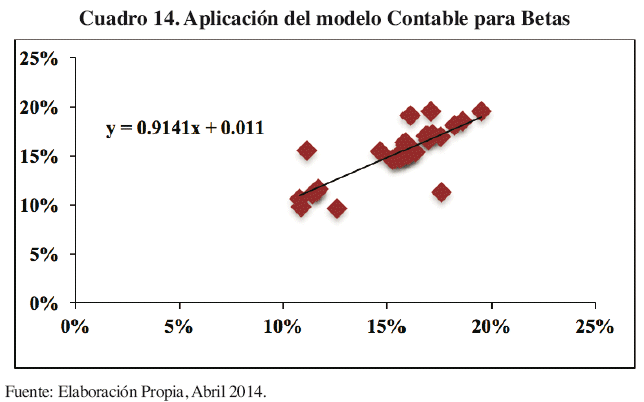
A continuación se muestra la aplicación práctica para el sujeto de estudio. El Cuadro 15 nos muestra que para el análisis contable del coeficiente Beta, los resultados pueden mostrarse de la siguiente manera; el BNB con un coeficiente de riesgo superior a la muestra (Beta 1,70), continuando con el BME con Beta 1,47 y considerando como relación mínima de riesgo-retorno al BEC (0,44).

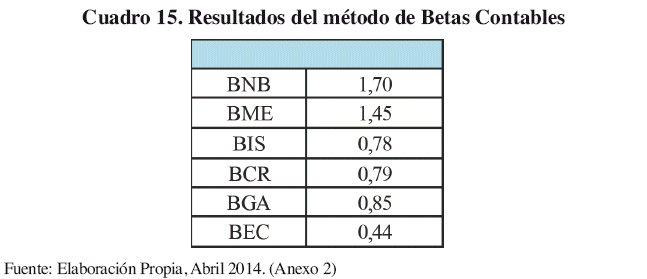
A primera vista el modelo de Betas Contables demuestra datos inversos al método de Betas Comparables [ver cuadro 13] lo que puede dar lugar a mantener cautela con estos datos por las siguientes razones:

• En los supuestos de regresión simple se asume que las variables en cuestión debieran ser estacionarias, lo cual no es una atribución característica del ROE histórico de los bancos estudiados

• La variables históricas mensuales utilizadas para este método, pueden diferir en gran magnitud si se considerase un cálculo del coeficiente Beta con datos de ROE anuales.

• La homoscedasticidad no predomina en los datos históricos del ROE, por el hecho de no ser variables estacionarias.

Beta Cualitativa

En la aplicación práctica del modelo cualitativo de Fernández, el riesgo sistemático del sujeto de estudio proviene de la metodología CAMEL, cuyos elementos o factores de análisis son adecuados en ponderaciones de niveles de riesgo dentro de las actividades del sujeto de estudio. A continuación el Cuadro 16 presenta la calificación subjetiva del riesgo sistemático para la media del sistema financiero bancario comercial.

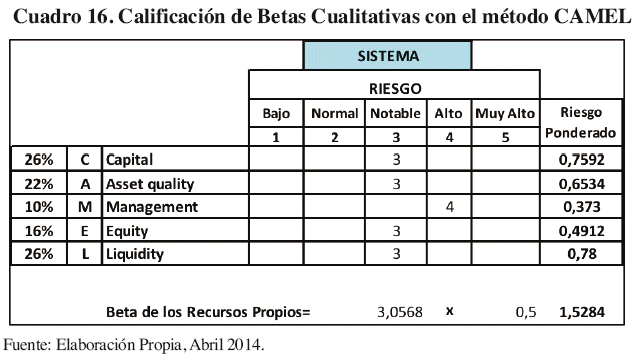
En consideración de los factores de riesgo inherentes en cada empresa mediante la metodología CAMEL, las aproximaciones prácticas de los bancos comerciales de Bolivia, mantienen coeficientes Betas con tendencias arriba de 1,50 en este método subjetivo. Solo dos bancos comerciales, el BIS y BCR, presentan coeficientes de 1,43 y 1,47 sucesivamente, lo cual los destaca como los menos sujetos a los cambios del mercado. Y con la asignación de riesgo sistemático más elevado se encuentra el BGA con 1,65 de coeficiente.

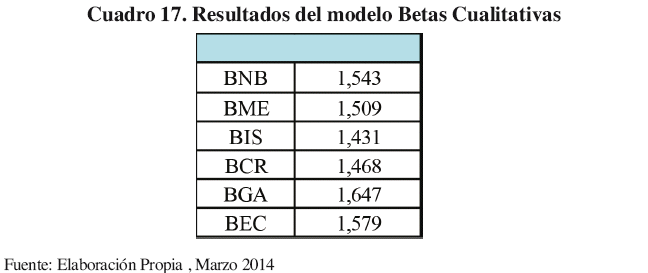
Observando los datos en el Cuadro 17, las calificaciones se encuentran muy cercanas entre sí, a pesar de que sus volúmenes de activos, tamaño de las obligaciones con el público, etc., tengan cantidades muy distintas. Una de las razones por la cual los resultados no mantienen significativos intervalos es:

• Los datos se agrupan alrededor de -1σ y +2σ, lo que se considera como un agrupamiento de datos.

• El cuadro 18 ejemplifica en una curva de distribución normal el Cuadro 8 dando por entendido que los ratios financieros escogidos para la metodología CAMEL calificados según su desviación estándar, no se distribuyen con normalidad (razón por la cual las calificaciones del Cuadro 17, varían entre 1,5 y 1,5)

•La ponderación de calificación varía respecto a la importancia que le pueda dar el evaluador a los factores de riesgo, y ello afecta significativamente a la determinación del coeficiente Beta.

•El parámetro de ponderación de riesgo es dado: por lo que si elegimos un parámetro de 0,5 las calificaciones de riesgo oscilaran entre -2,5 y 2,5. Pero si optamos por un parámetro de 0,6 las calificaciones van de -3 a +3, lo que demuestra un sesgo de calificaciones.

Comparación entre modelos

Los modelos aplicativos para la estimación del riesgo-retorno se muestran el Cuadro 19, para demostrar que sus resultados no convergen entre sí. Mediante su estimación se puede concluir que los datos obtenidos por medio de cada método tienen perspectivas no similares sobre el riesgo que puede afectar a una empresa.

 

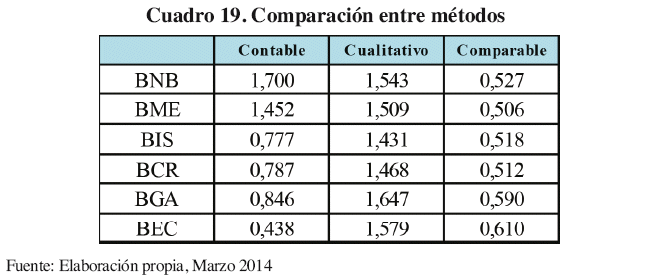
9. Propuesta

La siguiente propuesta está referida a realizar ajustes metodológicos a los métodos alternativos que se detallaron con anterioridad y cuyas estimaciones se realizaron con el fin de generar una idea de la relación entre los modelos, pero que en su primera aproximación, los coeficientes del riesgo-retorno presentaron poca o ninguna percepción de igualdad.

En el caso del método Contable (cuyos resultados provienen de rendimientos estáticos y varían según el tamaño y tipo de muestra (datos diarios, mensuales, anuales, etc.). se asume que la varianza del precio de las acciones no es constante, si se analizan los datos en un escenario internacional donde las cotizaciones en bolsa cambian finitas veces al día, podemos afirmar que el movimiento de los rendimientos de las acciones agrupa periodos de volatilidades altas y bajas, mencionando también el hecho de la falta de estacionalidad, entre otras debilidades.

Por otro lado, para el método de Betas cualitativas (propuesta por Fernández, que es una estimación analítica y a la cual le prosiguen otros métodos relacionado con el CAPM y la medición cualitativa de los factores de riesgo involucrados entre ellos el propuesto por Adolfo Rojas, nos vemos envueltos en la búsqueda de medir y calificar los factores que intervienen en el riesgo propio de la empresa de una manera más objetiva y precisa, sin necesidad de realizar la ponderación a dedo.

A continuación se presenta los ajustes que se realizaron al método contable y al método cualitativo, que gracias a las herramientas estadísticas se procedió a implementar a cada método, ajustes estadísticos y/o econométricos que disminuyeron la subjetividad al análisis y otras debilidades en los modelos para que sean aceptados como reemplazables a la estimación del coeficiente Beta a valores de mercado.

Modelo Contable-GARCH

Como se mencionó anteriormente, la extensión de los modelos ARCH, GARCH y ARCH-M, fue para solucionar el problema de los bastos movimientos de la varianza condicional del término de error, los cuales se dan con mayor intensidad en el mercado de activos.

El cálculo del riesgo sistemático con modelos heteroscedásticos se basó en datos del rendimiento sobre capital (ROE) del sujeto de estudio, que fueron proporcionados por la ASFI con datos desde Enero del 2011 a Diciembre del 2013.

Para resolver los problemas que limitan al modelo contable; realizamos una simulación de datos para obtener una serie más robusta y acercar los rendimientos a la estacionariedad requerida. Se realizó la generación de datos en base al método Monte Cario, con los datos mensuales del ROE (puesto que son los más utilizados teóricamente y el indicador está en base a los rendimientos del patrimonio).

Primero, se generaron 16, 32 y 64 datos aleatorios para verificar la estabilidad del coeficiente beta, en escenarios con mayor número de observaciones simuladas.

El Cuadro 20, muestra los datos generados mediante Monte Carlo. En las columnas contiguas al cálculo del coeficiente Beta para cada banco, se encuentra la diferencia en puntos porcentuales que existe entre cada resultado, esto con el fin de comprobar la estabilidad del nuevo cálculo. Se resalta entonces la inestabilidad que genera la simulación para cada banco. Así por ejemplo; para el BIS "simulación 64" genera una diferencia de 0,19 pp., respecto a la anterior simulación. También la simulación para el coeficiente Beta del BEC genera inestabilidad de 0,19 pp., respecto al anterior.

En conformidad con los resultados obtenidos en la simulación, a continuación se resalta la simulación elegida.

El coeficiente beta de la columna "β Simulación 16" es el que se utilizara en esta investigación: ya que es el paseo aleatorio de menor generación de datos simulados, y se considera que es el más confiable porque se entiende que; a mayor generación de datos aleatorios mayor es la varianza de error y menos confiable las pruebas estadísticas que se le puedan aplicar a la serie de tiempo.

Ya determinado la cantidad de datos aleatorios incorporados a la variable, se realiza su modelación mediante el modelo GARCH (1; 1). El Cuadro 21, da a conocer los nuevos valores estimados y los reportes de evaluación dentro de lo que es la evolución del modelo se percibe los siguientes valores; t-student, y el p-value.

El valor de t-student muestra la significatividad del modelo, los valores son distintos de 0 para el coeficiente de importancia. Por último, lo más importante en el análisis de las variables modeladas es el p-value, ya que demuestra los niveles de significatividad para rechazar o aceptar los modelos, para cada uno de los bancos el p-value rechaza la hipótesis nula de un coeficiente igual a 0.

El cuadro anterior da por aceptado la modelación casi en su totalidad por lo que para afirmar que el modelo está ausente de debilidades se considera el diagnóstico de residuos y el test-ARCH. El Cuadro 22 es un resumen de los correlogramas de residuos. Para la mayoría de los bancos favorablemente se demuestra ausencia de correlación con una significación por encima del 5%, y solo el BGA muestra correlación de residuos en sus dos primeras muestras (0,015 y 0,047) pero de todas maneras, el total de sus muestras concluyen con ausencia de correlación de residuos.

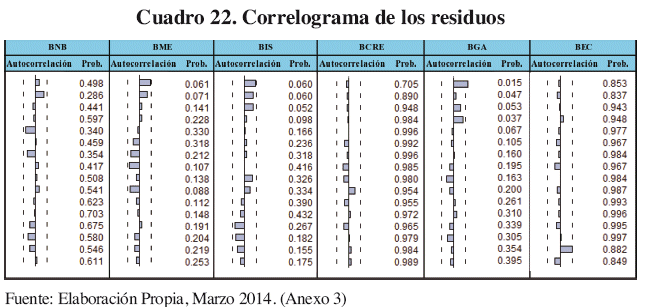
Para finalizar se realizó el test ARCH con la intención de comprobar si las variables han eliminado la heteroscedasticidad de la varianza del termino de error y el Cuadro 23 afirma ello, como se puede ver en la segunda fila, todas las variables se encuentran fuera de la zona crítica siendo el BME el de menor indicador, pero no menos confiable.

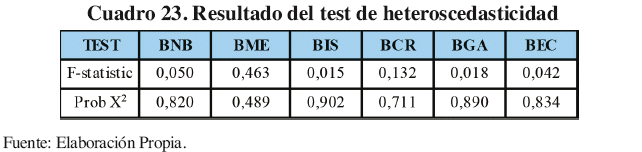
Los resultados obtenidos para el coeficiente Beta mediante los modelos heteroscedásticos, afirma con respaldos de los diagnósticos y evaluaciones, que se pueden eliminar muchas de las debilidades del modelo de Betas Contables. Las salidas de regresión y las evaluaciones al modelo se realizaron mediante el programa EViews®.

Modelo de Betas Cualitativa

Al realizarse la aproximación del coeficiente Beta Cualitativo en base a los estándares de análisis, ratios y calificación CAMEL otorgados por el UFIRS. Su calificación estuvo en base a las desviaciones estándar respecto a la media del sector, cada calificación tuvo su respaldo en las desviaciones estándar [Cuadro 9] y la ponderación de los factores se respaldó en el criterio del evaluador; pero como pudimos apreciar las calificaciones aún mantienen una alta subjetividad [Cuadro 17]

Por lo anteriormente descrito, es que se procedió a adecuar la metodología de calificación CAMEL que utiliza Pablo Fernández para la aproximación de Betas cualitativas. Primero se incorporó como ratios de evaluación de riesgos a los descritos con anterioridad que son proporcionados por la ASFI, y cuyos ratios son estandarizados para todos los bancos. Prosiguiendo, se descartó el uso de estimación mediante desviaciones estándar ya que los datos no mantienen una curva de normalidad Y se utilizó su homóloga la Mediana del Sistema de Bancos Comerciales (BNB, BUN⁴, BME, BIS, BCR, BGA, BEC). En consecuencia para la especificación de los rangos de calificación, se utilizó quintiles, que miden la dispersión total de los datos en intervalos que van de menor a mayor, tal y cual lo hace la calificación CAMEL. A continuación el Cuadro 24, muestra la localización general de los quintiles respecto a la calificación CAMEL, del 1 al 5 hacia la derecha para los indicadores que se encuentren dentro de los quintiles menores considerados mejores, y del 1 al 5 hacia la izquierda para los indicadores que se encuentre dentro los quintiles mayores a considerarse mejores.

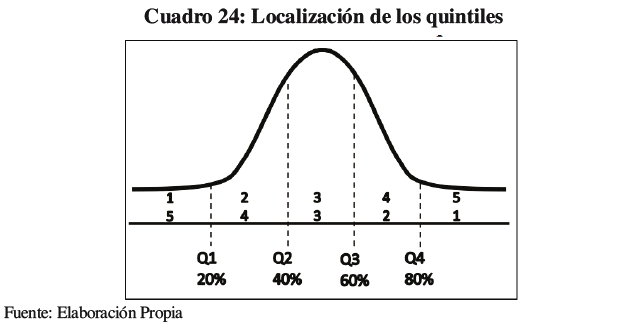
Gracias a este rango de estimación las calificaciones pueden ser más próximas a valores distintos de la mediana.

La ponderación utilizada para los factores de riesgo [ver Cuadro 16] es solo la expresión del criterio del evaluador, pero, como proposición el Cuadro 25, muestra ponderaciones para los indicadores financiero en base a un criterio objetivo presentado en Colombia como normativa para la selección de entidades financieras postulantes a participar del Indicador Bancario de Referencia (IBR)⁵.

Se tomó el criterio de esta ponderación en base a los siguientes fundamentos:

• Es una ponderación realizada en un país latinoamericano (lo que constituye significativa relación de políticas y desarrollo económico)

• Proceden de una institución de fiscalización financiera.

• Tiene una aplicación vigente

• Es entendido que procede de un previo estudio investigativo de la metodología.

Para concluir con el ajuste al modelo, volvemos a utilizar la herramienta estadística de los quintiles, esta vez para ajustar el parámetro 0,5 de riesgo: si bien en el método inicial este parámetro es dado, ahora optamos por acomodar las calificaciones obtenidas que se muestran en la fila "CALIFICACIÓN GENERAL" del Cuadro 26, en los centiles correspondientes al número de calificación.

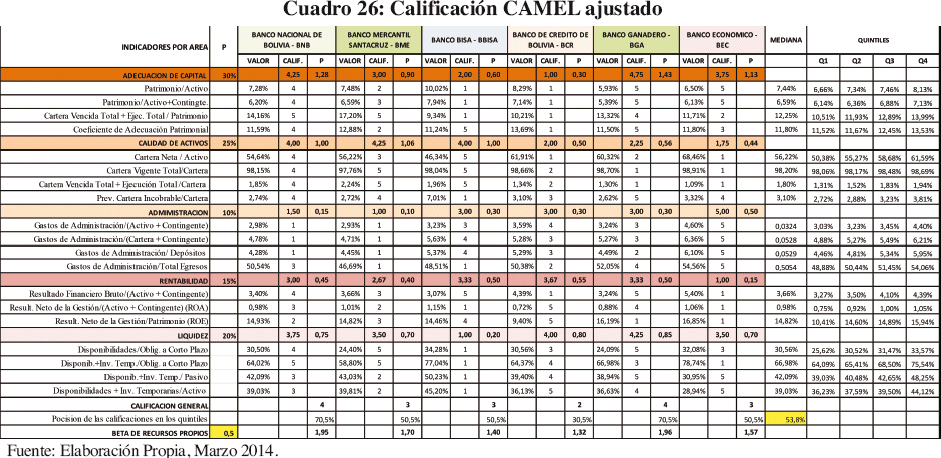
El Cuadro 27, demuestra gráficamente la ponderación del riesgo en base a la calificación CAMEL, para ponderar en base al riesgo la fila "CALIFICACIÓN GENERAL" del Cuadro 26.

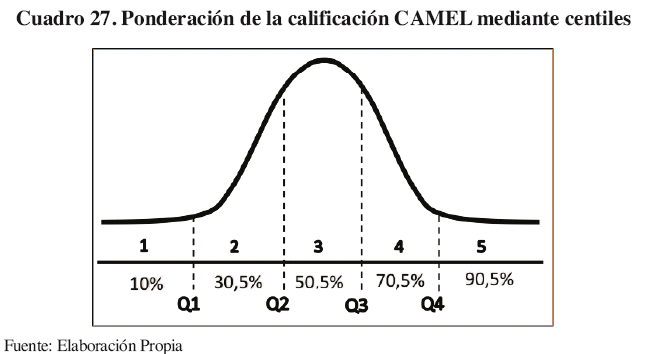
El promedio de estas ponderaciones mediante centiles, se muestras en la fila "Posición de las calificaciones en los quintiles", donde este nuevo riesgo 53,8% viene a ser el parámetro del riesgo obtenido mediante las calificaciones del CAMEL.

El Cuadro 27, también muestra los cambios realizados a la ponderación de los factores de riesgo, la incorporación de los quintiles en la calificación de los indicadores y por último los ajustes al parámetro de riesgo de la empresa.

Con la nueva estructuración del modelo obtenemos coeficientes Beta menos subjetivos y con respaldos académicos y estadísticos: para el BNB (1,95), BME (1,70), BIS (1,40), BCR (1,32), BGA (1,96) y BEC (1,57).

 

Conclusiones

El método de Betas Contables se ve afectado por el número de observaciones, aspecto que no es completamente subsanado a partir de la inclusión de datos simulados debido a la composición de señales (estacionalidad, ciclo, tendencia) inmersas en las series de tiempo financieras.

La aproximación por Betas Cualitativas posee un alto grado de subjetividad por parte de la opinión experta, aspecto que puede ser acotado mediante el uso de medidas estadísticas de posición.

Los resultados obtenidos a través de los modelos alternativos ajustados confirman la utilidad metodológica de la propuesta, por tanto, dichas aproximaciones pueden ser utilizados por especialistas en valoración, consultores financieros, proyectistas, agencias de bolsa, asesores de inversión, entre otros, al momento de efectuar cálculos propios de la valoración de empresas, procesos de fusión, adquisición y desinversión de empresas en países de vías de desarrollo.

 

Notas

1. LOPEZ DUMRAUF, Guillermo; "Finanzas Corporativas", www.duraufnet.com.ar. Fecha de consulta; 31/07/13.

2. Entrevista al Gerente General Jaime Dunn De Ávila NAFIBO Sociedad de Titularización La Bolsa, Argentina(2010).

3. Compuesto por: Capital Social + Aportes No Capitalizados + Reservas - Pérdidas acumuladas.

4. Se considera al Banco Unión, porque a pesar de ser un banco con porcentajes de participación Estatal, compite directamente con los bancos comerciales privados.

5. El Indicador Bancario de Referencia es una tasa de interés de corto plazo para el precio al que los agentes participantes en sus esquemas de formación están dispuestos a ofrecer o aceptar sobre los recursos en el mercado monetario.

6. ASOBANCARIA- Normativa; "Metodología de la selección de las entidades Financieras que participaran en el esquema del indicador bancario de referencia" 2013. www.asobancaria.com (Consultado en fecha: 22/05/2014).

 

Referencias Bibliográficas

Anderson-Sweeney-Willams (2008). Estadística para Administración y Economía, 10^ma. Ed. Editorial: Cengage Learning.

Besley-Eugene (2009). Fundamentos de Administración Financiera, 4^ta. Ed. Editorial: Mc Graw Hill.         [ Links ]

Damodar, Gujarati (2006). Principios de Econometría 3^ra Ed. Editorial Mc Graw Hill.

Damodaran, Aswath (2010). Applied Corporate Finance, 3^TH Edition, John Wiley & Son, Inc.         [ Links ]

Diaz-Santacruz (2010). Decisiones Financieras Bajo Incertidumbre, Ediciones: Escuela Colombiana de Ingeniería.

De Lara, Alfonso (2005). Medición y Control de Riesgos Financieros, 3^ra Ed. Editorial: Limusa.

Elbaum, Marcelo (2006). Administración de Carteras de Inversión, 2da Ed. MACHI.         [ Links ]

Estrada, Javier (2002). The Cost Of Equity In Emerging Markets: A Downside Risk Approach, IESE (Barcelona, Spain) Department of Finance. Elsevier.         [ Links ]

Entrevista al Gerente General Jaime Dunn De Ávila NAFIBO Sociedad de Titularización La Bolsa, Argentina (2010)        [ Links ]

Escoto Leiva (2007). Roxana: Banca Comercial, 1^ra Ed. Editorial: Euned.

Fabris, Julio (2009). Econometría Financiera Modelos y Pronósticos utilizando QMS, EViews®" 1^ra Ed. Omicron Systems S.A.

Feria Domínguez (2005). José Manuel; El Riesgo de Mercado: Su Medición y Control, Ediciones: DELTA.

Fernández, Pablo (2010). Valoración de Empresas, 3^ra Ed. Editorial: Gestión 2000.         [ Links ]

Fundacion Milenio (2013). Los Conflictos en el 2012, La Paz.         [ Links ]

Gómez-Bezares, (2004); Lecturas sobre Gestión de Carteras, (Artículos preparados en el Departamento de Finanzas de la Universidad Comercial de Deusto).         [ Links ]

Gómez, Molina (2011). Supuestos Implícitos en la Utilización del Capital Asset Pricing Model-CAPM- Para el Cálculo del Capital Propio-Equity, Documento Doctorado, ISSN 2248-4752. FCE-CID No 1.FCE Centro Editorial.         [ Links ]

Guzmán Plata, María de la Paz (1998). Los modelos CAPM y ARCH-M obtención de los coeficientes beta para una muestra de 33 acciones que cotizan en la Bolsa Mexicana de Valores, Revista Economía: Teoría y Práctica. Ed. Nueva Época, Numero 9.

Jarillo-Jiménez (2002). Sector Bancario y Coyuntura Económica. El caso Colombiano 1990-2000, 1ra. Ed. Universidad de EAFIT.

Jimenez, John (2012). Documento de Tesis: "Betas Contables", Colegio De Estudios Superiores En Administración.

Lopez Dumrauf, Guillermo (2010). Finanzas Corporativas, 2^da Ed. Ediciones: ALFAOMEGA.         [ Links ]

Loreto-Molano (2009). Capital Asset Pricing Model -Robert Merton; Teoría y Evidencia Empírica Para Colombia 2001-2007, Cuadernos Latinoamericanos de Administración, Vol. IV No. 6, 2008-ISSN 1900-5016.

Madura, Jeff (2010). Mercado e Instituciones Financieras, 8^va Ed. Cengage Learning.         [ Links ]

Markowitz, H.M (1952); "Portfolio Selection", Journal of Finance, 7, (1)        [ Links ]

Márquez de la Cruz, Elena (2001). La elasticidad de sustitución intertemporal y el consumo duradero: un análisis para el mercado de valores español, Universidad Complutense de Madrid Facultad de CC. Económicas y Empresariales.         [ Links ]

Martínez, Clemencia (2007). Estado del arte de las finanzas, Universidad Santo Tomas.         [ Links ]

Nieto, Belén (2001). Los Modelos Multifactoriales De Valoración De Activos: Un Análisis Empírico Comparativo, Tesis de Doctorado,

WP-EC 2001-19, Universidad de Alicante. Depto. de Economía Financiera.

Nistal Bravo, Darlen (2010). El Método CAMEL como método de análisis utilizado por las Instituciones Financieras, COFIN Habana Revista de la Facultad de Contabilidad y Finanzas de la Universidad de la Habana.         [ Links ]

Pereiro, Luis E. (2010). Universidad Torcuato Di Tella, PAPER; "The Beta Dilemma in Emerging Markets" Revista; Journal of Applied Corporate Finance. Vol. 22. Núm. 4. Morgan Stanley Publication, EE.UU.

Pindyck, Robert (2000). Econometría, 4^ta. Ed. Editorial: Mac Graw Hill.         [ Links ]

Rubio, Fernando (2004). Modelo de tres factores en España, Paper. Editorial: Universidad de Valparaiso.

Rubio- Mari (2001). Economía Financiera, 1^ra Ed. Editorial: Antoni Bosch, España (2001)

Smith, Adam (1776). La Riqueza De Las Naciones, The Journal Finance, Vol. 7.

Valencia-Araujo (2008). Fundamentos de Inferencia Estadística, 1^ra Ed. Editorial: Pontificia Universidad Javeriana. (2008)

Vernimmen-Le-Quiry-Dalocchio & Salvy (2010). Corporate Finance Theory and Practice, 2d^a. Ed. John Wiley & Son, Ltd.

 

Citar como:

VIDAURRE Ortega, Juana Isabel (2016). "Las Finanzas Conductuales, el Alfabetismo Financiero y su Impacto en la Toma de Decisiones Financieras, el Bienestar Económico y la Felicidad". Perspectivas, Año 19 - N° 37 - mayo 2016. pp. 41-74. Universidad Católica Boliviana "San Pablo", Unidad Académica Regional Cochabamba. Clasificación JEL: G0, G19.

 

Recepción: 01-3-2016

Aprobación: 06-4-2016