Artículo Científico

 

Un operador de Sheffer en la Lógica IGR_P

 

A Sheffer operator in IGR_P-Logic

 

 

Oscar R. Pino Ortiz

Universidad Católica Boliviana, Cochabamba, Bolivia Los Nogales 2030 Cbba

pino@ucbcba.edu.bo

Recibido: mayo 2018
Aceptado: agosto 2018

 

 

---

Resumen: Una vez explicitado el nexo entre los operadores de una lógica p-multivaluada (p primo) y el anillo de polinomios Z_p[x,y], se demuestra de forma algébrica que la lógica a p valores IGRp admite como operador de tipo Sheffer al operador correspondiente del polinomio

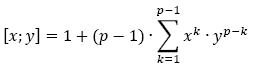
Palabras clave: Lógica, Multivaluada, Sheffer, IGRp

---

Abstract: Defined a functor from a p-multivalued logic (p prime) and the polynomial ring Z_p[x,y], it is demonstrate by algebraic arguments the existence of a Sheffer operator in the p-valued logic IGR_P. The polynomial associated to that operator is:

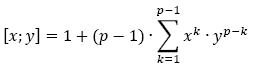
Key words: Logic, Multivalued, Sheffer, IGRp

---

 

 

1     Introducción

En un artículo anterior [7] tuvimos la ocasión de establecer la existencia de un functor natural entre los operadores lógicos L(p) de IGR_P y los polinomios del anillo Z_p [x;y]. Así mismo pudimos construir un operador de tipo Sheffer para la lógica IGR₃. En el este artículo presentamos la demostración de la existencia de un operador de tipo Sheffer para la lógica p-valuada (con p primo) IGR_P. Lo interesante de esta demostración es que mejora en sencillez y naturalidad la propuesta por Emil Post.

El primer resultado mencionado nos permitirá establecer un nexo entre L(p) y el anillo de matrices cuadradas M_p[Z_p].

 

2     Observación

Todo polinomio de Z_p[x;y] determina los valores que toma y está totalmente determinado por los mismos. Es decir, existe una biyección natural entre Z_p[x;y] y el anillo M_p[Z_p].

En efecto, los valores que el polinomio r toma, forman la matriz M_r cuyo coeficiente m_k+1,l+1 no es sino r(k;l) con k,l {0;...;p-1}.

Obviamente la resolución del sistema

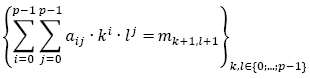
permite reencontrar los coeficientes a_ij del polinomio r.

3     Objetivo

Nuestro objetivo será el de mostrar que con el polinomio

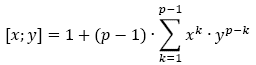
podemos construir todos los polinomios de Z_p [x;y] o, lo que es lo mismo, todas las matrices de M_p[Z_p].

 

4     Estudio de [x; y]

Definamos, por comodidad:           

Entonces

Proposición 1

Si a y b Z_p, las propiedades de son las siguientes:

1.

2. es asociativa

3. es conmutativa

4. es idempotente

En efecto:

1.

a) Si a = b entonces

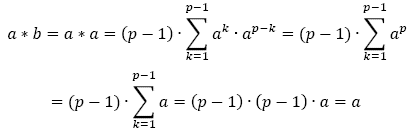
b) Si a ≠ b entonces

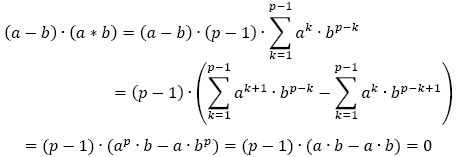
Como (a - b) ≠ 0 entonces a b = 0

2. Como la asociatividad es evidente.

3. La conmutatividad a b = b a es evidente

4. La idempotencia a a = a se mostró en 1.

Corolario 1

Si r,s Z_p[x] entonces

Corolario 2

induce, sobre el anillo M_p[Z_p], una operación asociativa, conmutativa e idempotente

definida por        

Corolario 3

Mostrar que el operador asociado al polinomio [x;y] = 1 + x y es un operador de tipo Sheffer, es equivalente a mostrar que con el operador inducido:

donde a es la matriz cuyos coeficientes son todos iguales a a y + es la suma habitual, podemos construir todas las matrices de M_p[Z_p], y esto a partir de las matrices asociadas a los polinomios x y y.

Teorema 1

El operador matricial [M;N] = 1 + M&N es tal que con él podemos construir todas las matrices de M_p[Z_p], a partir de las matrices

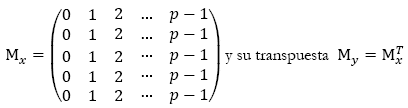
Demostración

Notemos que M_x y M_y son las matrices de valores de los polinomios x y y. Por un cálculo sencillo vemos que:

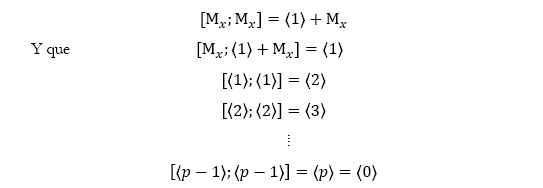
Por lo tanto a es construible a partir de M_x.

Ahora bien, observamos que:

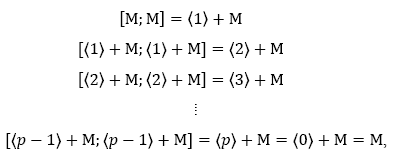
y también que

resultado que interpretamos de la siguiente manera:

"[M;N] es construible si y sólo si M&N lo es"

Definición

Llamamos "descomposición numérica" de M al conjunto de matrices resultantes de efectuar las operaciones a&M para todo a {0; 1; 2; ...; p - 1}.

Afirmación 1

Las matrices a&M son construibles por medio de & a partir de M_x y M_y.

Prueba

Como a + M_x es construible, b + M_y y c, tenemos que

es construible. La matriz resultante tiene una de sus entradas igual a c y todas las otras igual a 0. Efectivamente M_x tiene una sola columna (la columna de índice c - a + 1), con coeficientes iguales a c - a, por lo tanto a + M_x tiene una sola columna con coeficientes iguales a c. De idéntica manera M_y tiene una sola fila (la fila de índice c - b + 1) con coeficientes iguales a c - b, por lo tanto b + M_y tiene una sola fila con coeficientes iguales a c. Así pues (a + M_x)&(b+ M_y) tiene una sola entrada (intersección de la columna con la fila) igual a c. Finalmente al efectuar &c, todos los otros coeficientes serán 0.

Además las matrices (a + M_x)&(b + M_y)&c y (a' + M_x)&(b' + M_y)&c' son iguales si y sólo si a = a', b = b' y c = c', por lo que deducimos que el conjunto:

contiene todas las matrices que tienen c en sólo una de sus entradas y 0 en las otras. De este modo vemos que todas ellas son construibles, puesto que se las puede obtener a partir operando con & ciertas matrices construibles.

Afirmación 2

Las matrices cuyos coeficientes son ó 0 ó c son construibles.

Prueba

Llamemos C(i;j) a la matriz que tiene en la entrada (i;j) el valor c y 0 en todas las otras. Ya sabemos que C(i;j) es construible.

Consideremos ahora la matriz C'(i;j) = (p - c) + C(i;j). Se trata de la matriz que tiene 0 en la entrada (i;j) y p - c en las otras. Si según conveniencia, tomamos una sucesión de estas matrices

Y las combinamos

Obtenemos una matriz cuyos coeficientes son 0 para os índices indicados y p - c para el resto.

Por consiguiente la matriz

Es la matriz con el valor c en las entradas indicadas y 0 en las otras. Queda demostrado que las matrices cuyos coeficientes son o bien c o bien 0 son construibles.

 

Afirmación 3

Si tenemos la descomposición numérica de M, podemos reconstruir M mediante &.

Prueba

Si la descomposición numérica de M consiste en sólo la matriz nula, no hay nada que demostrar pues ello significa que M = 0 y 0 es construible.

Si no es así, sean a₁&M, a₂&M, a₃&M,..., a_m&M las matrices de la descomposición numérica de M donde a_k {0; 1;..; p - 1} remuneradas luego de haber excluido los casos en los que se obtiene la matriz nula.

Observamos que

Vamos a mostrar, por inducción sobre m, que M es construible:

1. Para todo b Z_p tenemos que b&M es construible. Por lo tanto si m = 1, está demostrado.

2. Supongamos que cualesquiera que sean b₁, b₂, b₃, ...,b_k Z_p, con b_¡ ≠ b_j si i ≠ j, tenemos que b₁&M + b₂&M +...+b_k&M es construible. Sea b_k+1 diferente a los anteriores. Vamos a mostrar que

es construible.

Notemos M_k = b₁&M + b₂&M + ... + b_k&M

Notemos = b₁ - b_k+1&M + b₂ - b_k+1&M + ... + b_k - b_k+1&M

Por hipótesis de inducción es construible.

Consideremos b_k+1 + . Esta matriz tiene b_¡ donde tenía b_¡ - b_k-1 para i {1,..., k} y tiene b_k+1 donde tenía 0.

Seguidamente notemos

Por hipótesis de inducción es construible.

Seguidamente consideremos b_k + . Esta matriz tiene b_¡ donde tenía b_i - b_k para i {1,..., k - 1, k + 1} y tiene b_k donde tenía 0.

Finalmente la matriz

es tal que tiene b_¡ donde tenía b_¡ para i {1,..., k} , tiene b_k+1 donde tenía b_k+1 y tiene 0 donde ambas tenían 0 simultáneamente. Es decir:

con lo queda demostrado que M es construible.

 

5     Conclusión

El operador lógico de la lógica IGRp, correspondiente al polinomio

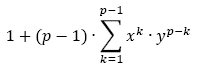
de Z_p [x;y], es de tipo Sheffer.

 

Referencias Bibliográficas

[1] Guzmán de Rojas, I. (2007). Logica Aymara y Futurología. La Paz: Editorial Santín.         [ Links ]

[2] Stojmenovic I., (1988). On Sheffer symmetric functions in three valued logic. Discrete Applied Mathematics 22, North-Holland.

[3] Foxley E., (1962) The determination of all Sheffer funtions in 3-valued logic, using a logical computer. Notre Dame Journal of Formal Logic, Volume III, Number 1. Nottingham, England.

[4] J J O'Connor & E F Robertson (2001). Emil Leon Post. Mac tutor: History of mathematics. Recuperado de http://www.history.mcs.st-andrews.ac.uk/Biographies/Post.html.         [ Links ]

[5] Pino O., Morales Z. (2015) Un operador de Sheffer en la Lógica IGR3. Acta Nova, Vol 7, Nº1. Cochabamba, Bolivia. http://www.academia.edu/1399119/Basic_many-valued_logic.