Services on Demand
Journal
Article
Indicators
Related links
Share
Acta Nova
On-line version ISSN 1683-0789
RevActaNova. vol.8 no.1 Cochabamba Mar. 2017
ARTÍCULO CIENTÍFICO
Análisis y Aplicación de RNA's a Capas de Acero Borurado
Analysis and Application of ANN to Layers of Bored Steel
C. I. Mota-Hernández1, R. Alvarado-Corona1, J. L. Félix-Hernández3,O. Morales-Matamoros2
1UAEH, Escuela Superior de Cd. Sahagún, ESIME-Zacatenco, curthis@gmail.com
1UAEH, Escuela Superior de Cd. Sahagún SARACS-SEPI-ESIME-IPN, ralvcor@gmail.com,
2IPN, SEPI, ESIME-Zacatenco, Departamento de Ingeniería de Sistemas, curthis@hotmail.com,
3Universidad Juárez Autónoma de Tabasco (UJAT), curthis@gmail.com
Recibido: 29 de septiembre 2016
Aceptado: 15 de enero 2017
Resumen: Se analizaron y aplicaron tres modelos de Redes Neuronales Artificiales (RNA's): Perceptrón multicapa (MLP), función de base radial (RBF) y la combinación de ambos modelos (RBF & MLP), para obtener el valor de tenacidad a la fractura para los aceros borurados AISI 1045, AISI 1018 y AISI M2. Los aceros fueron expuestos al tratamiento de borurización en pasta, mediante el modelo de grietas tipo Palmqvist, aplicando el modelo de agrietamiento para la evaluación experimental de la tenacidad a la fractura propuesto por Balankin y Campos a través de la modificación del modelo de T. Laugier. Los datos de entrada para cada modelo de red toman en cuenta el tipo de acero borurado, el espesor de capa generado, la distancia de la indentación y la carga de indentación. Las redes fueron entrenadas con datos obtenidos experimentalmente bajo el ensayo de microindentación Vickers sobre las capas de boruros de hierro a diferentes cargas. Los datos de la tenacidad a la fractura de las capas de boruros de hierro son comparados con datos experimentales, obteniendo errores del 5% para ambos modelos de redes neuronales.
PALABRAS CLAVE: RNA's, Borurización, Tenacidad a la fractura, Indentación
Abstract: Three models of artificial neural networks were analysed and applied: Multilayer Perceptron (MLP), Radial Basis Function Network (BRFN) and the combination of both models (RBFN & MLP) for the value of fracture toughness for boriding steels AISI 1045, AISI 1018 and AISI M2. The steels were exposed to a boriding treatment paste, using the model of Palmqvist type cracks, applying the model to the experimental cracking assessment toughness Balankin proposed by Campos and through the modification of the model T. Laugier fracture. The input data for each grid model taking into account the type of steel boriding, the generated layer thickness, the distance of the indentation and the indentation load. The networks were trained with data obtained experimentally under Vickers microindentation testing on iron boride layers at different loads. The data of the fracture toughness of the iron boride layer are compared with experimental data, obtaining errors of 5% for both models of neural networks.
KEYWORDS: ANN's, Boriding, Fracture toughness, Indentation
1. Introducción
El emplear procesos de tratamientos termoquímicos aporta en forma relevante para la construcción de maquinaria y equipo, lográndose con éstos un aumento de la durabilidad y propiedades mecánicas de sus elementos, considerando que pueden obtenerse aleaciones superficiales de alta calidad sobre metales de bajas cualidades, aumentando la resistencia al contacto, a la fatiga, a la oxidación y al desgaste.
Al aplicar técnicas de Inteligencia Artificial (IA), en particular, las Redes Neuronales Artificiales y dentro de las mismas, topologías diversas, se busca aportar, robustecer y sintetizar la comprensión de los principales fenómenos involucrados en dicho proceso, ya que al implementar RNA's se consigue una mejor solución al reducir el número de parámetros mínimos necesarios para determinar propiedades mecánicas, como es el caso explícito de la tenacidad a la fractura [1,2].
2. Fundamentos Teóricos
Se utilizó la tenacidad a la fractura evaluada en aceros borurados AISI 1045, M2 y AISI 1018 mediante el modelo de grietas tipo Palmqvist. La superficie del acero fue endurecida por el tratamiento termoquímico de borurización en pasta a diferentes temperaturas, empleando como medio borurante distintos espesores de pasta de carburo de boro sobre la superficie del material. La tenacidad a la fractura de las capas boruradas se determinó por el ensayo de microindentación Vickers manteniendo constante la distancia de indentación desde la superficie del acero, para todo el conjunto experimental del proceso termoquímico. El modelo de agrietamiento para la evaluación experimental de la tenacidad a la fractura es propuesto por Balankin y Campos a través de la modificación del modelo de T. Laugier [1,2].
El proceso para calcular el valor de la tenacidad a la fractura (KIC) por indentación implica la aplicación de pruebas estandarizadas de microdureza Vickers, así como las mediciones de grietas generadas en escala de micras [3-5].
Para la determinación KIC por microindentación de la fase Fe2B, obtenida sobre la superficie de un acero estructural AISI 1045 y un acero AISI 1018, se aplica la siguiente ecuación [6]:
![]()
En tanto que para determinar KIC por microindentación, obtenida sobre la superficie de un acero M2, la ecuación que se aplica es [6]:
![]()
En donde:
KIC= Tenacidad a la Fractura
E = Módulo de Young
HV = Dureza Vickers
a = longitud de la diagonal del indentador Vickers
l = Longitud de la mitad de la diagonal de la indentación
Es importante considerar el tipo de problema a resolver al trabajar con RNA's. En el caso de la salida que se desea obtener al finalizar el entrenamiento de las redes es de aproximación de funciones, siendo la red perceptrón multicapa (MLP) recomendado para la solución de estos problemas [7]. Sin embargo, por las características de la serie de muestras que se cuenta (74 muestras) una de las redes más comunes para el entrenamiento con pocos datos es la red de función de base radial ((RBFN), ya que, se utiliza para aproximar funciones con un conjunto de muestras menor a 100 [8].
3. Materiales y Métodos
El software utilizado para el desarrollo de las Redes Neuronales Artificiales fue Neurosolutions [9] y los modelos utilizados fueron: (1) Perceptrón multicapa (MLP, por sus siglas en ingles), (2) Base radial (RBFN, por sus siglas en ingles) y (3) una combinación de ambas, por ser los más populares y apropiados para una gran variedad de problemas en ingeniería, con entrenamiento supervisado para la primera e híbrido para la segunda, es decir, combina el entrenamiento supervisado y no supervisado. Posteriormente se construyó una red, combinando los dos modelos de red anteriores, a fin de comprobar su eficacia.
El Diseño de la MLP utilizada para la obtención de KIC para los aceros borurados AISI 1045, AISI M2 y AISI 1018 se ilustra en la figura 1.

La MLP está adiestrada con el algoritmo estándar de retropropagación del error con los datos obtenidos experimentalmente de: espesor de capa (EC), distancia (d) y carga de la indentación (P), así como tipo de acero (TA), teniendo como salida deseada el valor de KIC.
Las características de la MLP diseñada para la obtención de KIC de los aceros borurados AISI 1045, AISI M2 y AISI 1018 se muestran en la tabla 1.

De igual forma que con el diseño de la MLP, el diseño de la RBFN (figura 2) se utiliza para los aceros borurados AISI 1045, AISI 1018 y AISI M2.
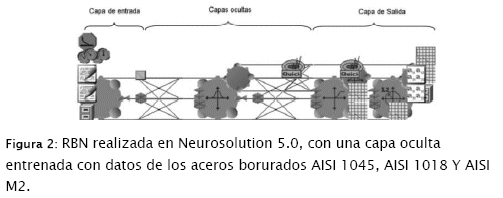
La RBFN diseñada, está constituida por una función estática de Gauss en su única capa oculta y, al igual que la MLP, está entrenada con los mismos datos de las variables de entrada y salida (EC, TA, d, P, KIC).
Las características de la RBFN, diseñada para la obtención de KIC de los aceros AISI 1045, AISI M2 y AISI 1018, se muestran en la tabla 2.

Al combinar la RBFN y la MLP, se obtuvo la red mostrada en la figura 3.4, también utilizada para los aceros borurados AISI 1045, AISI 1018 y AISI M2.

La red diseñada a partir de la combinación RBFN-MLP está constituida por una función estática de Gauss en la primera capa oculta y en las dos siguientes capas con funciones sigmoidal y tangencial, respectivamente.
Las características de la red diseñada para la obtención de KIC de los aceros AISI 1045, AISI M2 y AISI 1018, se muestran en la tabla 3.

Como ya se mencionó al inicio de este apartado, las RNA's fueron realizadas en el software Neurosolutions v.5.0, el cual permite al usuario construir, entrenar y probar redes neuronales completamente desde diversas aplicaciones.
Las fases que se sugieren realizar durante el entrenamiento de una RNA son tres.
Primera Fase: se entrena la red hasta que se obtienen los mejores pesos y se estabiliza. Durante la etapa de entrenamiento, al número de veces que se deben ingresar los datos de entrada y los deseados se le conoce como número de ciclos (ver tablas 1, 2 y 3). Cuando la red aprende, el error tiende a cero.
Segunda Fase: se valida la red. Durante el entrenamiento la red es alimentada también con los datos de entrada del conjunto de validación, y la información generada es comparada con los datos de salida del mismo conjunto de validación. El rendimiento de la red es recopilado y se crea un informe que exhibe los resultados, tanto del entrenamiento como de la comprobación dentro de la validación [11].
El informe generado en el entrenamiento y la validación contiene la información siguiente [10]:
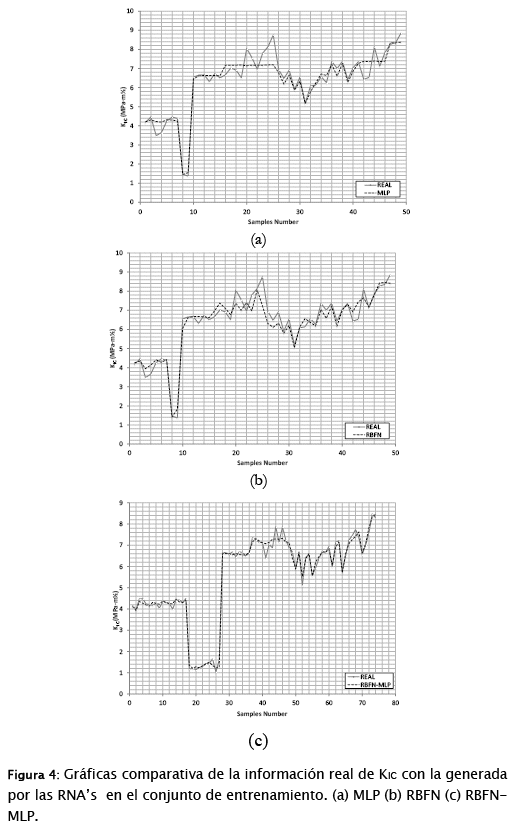
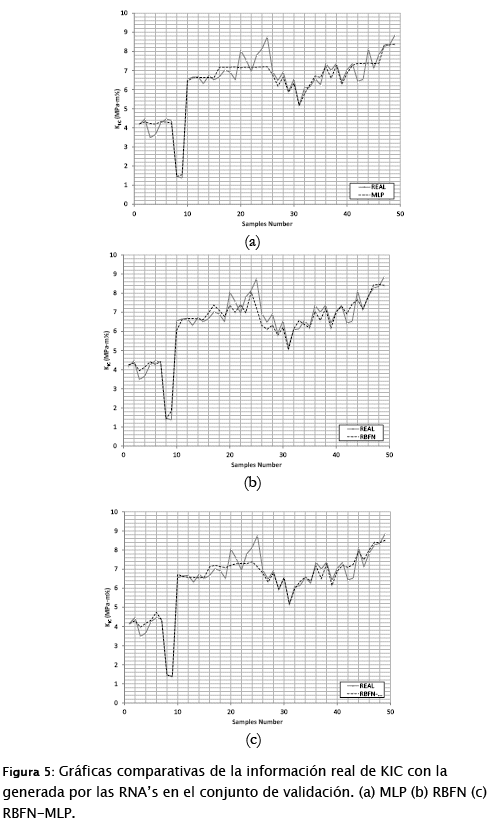
1. Gráfica de salida en la red y salida deseada, ambas se grafican (figuras 4 y 5).
2. Se informa el error cuadrático medio (MSE), el error cuadrático medio normalizado (NMSE) y el porcentaje de error generado (tabla 5) [12].
Tercera Fase: se aplican los datos desconocidos a la RNA, ya entrenada y validada, para observar los resultados que brinda la RNA.
Para el entrenamiento de las RNA's se utilizaron el tipo de acero, el valor de espesor de capa obtenido durante el tratamiento de borurización, la distancia y la carga de la indentación y los calculados de KIC.
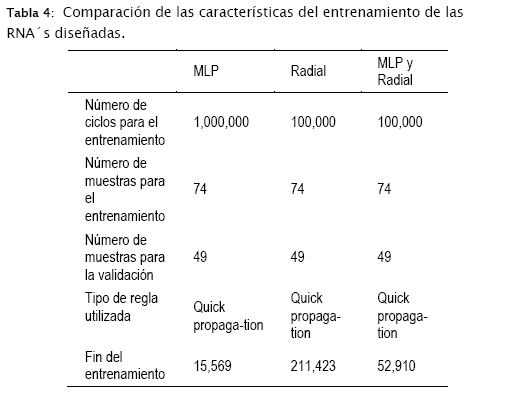
Dentro de las características del entrenamiento se consideró el número de ciclos, el número de muestras obtenidas y el tipo de regla de aprendizaje que se muestran en la tabla 4, la cual de manera explícita presenta el detalle de la comparación de los principales elementos involucrados en el entrenamiento para considerar a la red robusta y sólida [13,14].
4. Resultados y Discusión
En la etapa de entrenamiento de las 3 RNA's desarrolladas, el comportamiento de los valores generados de KIC en el conjunto de muestras introducidas para dicha etapa son muy similares a los datos de KIC obtenidos a partir de las ecuaciones (1) y (2). Se observa que la RNA con el menor error fue la RBFN-MLP: 3.05% (figura 4).
En la figura 5 se observa la salida deseada para el conjunto de validación, comparada con la información generada por las RNA's al finalizar el entrenamiento.
El paso final consistió en la etapa de producción, en donde se introducen únicamente los datos de entrada a las RNA's para que la red genere la información del valor de tenacidad a la fractura, KIC (ver figura 6).
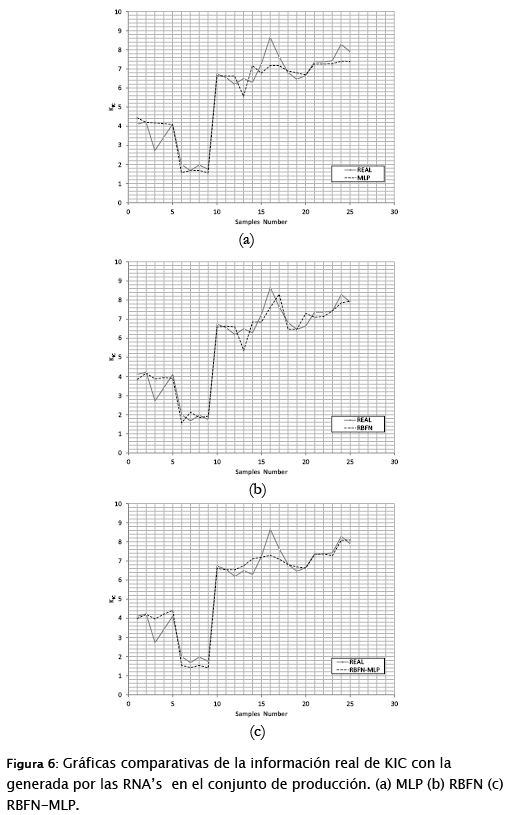
La tabla 5 muestra una comparación de los resultados obtenidos en las tres RNA's. En dicha tabla se observa que el porcentaje de error más bajo se obtuvo en el RBFN-MLP, el cual fue de 4.14% en el conjunto de validación. Cabe mencionar que, a pesar de que el error de entrenamiento más bajo obtenido (red RBFN-MLP) fue de 3.05%, se toma en cuenta el error de la validación, ya que es éste el que determina el que se obtendrá en la producción de datos [15,16].
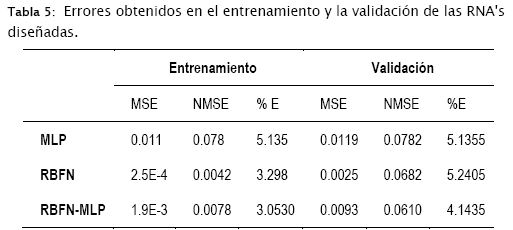
Algunos factores que intervinieron para obtener porcentajes de error bajos fueron el número de capas ocultas y el número de neuronas contenidas en cada capa oculta. Es de destacarse que, para el caso de la MLP, mayor número de capas ocultas no implica que se generará mayor exactitud en el resultado obtenido. En el caso de la RBFN, la exactitud del resultado obtenido tampoco depende del número de elementos en su única capa oculta ya que existen varios factores que intervienen en el diseño de una RNA [17].
5. Conclusiones
Para el diseño de una RNA se tiene que escoger el modelo de red que más se adecue a la resolución del problema, al número de muestras que se tienen y al error esperado. Posteriormente, se eligen la funciones de activación que se van a utilizar (en el caso de las redes tipo MPL), el número de capas y, para ambos modelos de red, el número de neuronas en las capas ocultas. Finalmente, hay que contemplar el tipo de regla de aprendizaje y considerar que es también importante utilizar de las muestras un porcentaje para el entrenamiento y otro para la valoración de la red creada
Se puede observar que para ambas redes el número de neuronas de entrada y de salida viene dado por el número de variables que definen el problema, y que, a pesar de que actualmente hay fórmulas para calcular el comportamiento de la red por capas, el mejoramiento y perfeccionamiento de una red se realiza más bien por prueba y error.
Para la implementación de las RNA's es imprescindible escoger el modelo de red que más se adecue a la resolución del problema, al número de muestras que se tienen y al error esperado.
La MLP es un modelo RNA de tipo aproximación porque lo que se busca generar un valor aproximado de algún parámetro, en este caso Kic de los aceros borurados AISI 1045, AI SI 1018, AISI M2. Sin embargo, la RBFN es una buena opción para situaciones en las que no se tiene gran número de muestras, como es este caso (74). Es por esta razón que al combinar ambos modelos de RNA's el error generado fue mucho menor, ya que tanto el MLP y la RBFN son factibles para resolver problemas del mismo tipo, ambas poseen sus neuronas agrupadas en capas y las conexiones están dirigidas hacia adelante, es decir, no son recurrentes.
Sin embargo, estos dos tipos de redes presentan también algunas diferencias:
Número de capas ocultas: una única capa para la RBFN y tantas capas como se desee para el MLP.
Distribución de los pesos: en la RBFN las conexiones de la capa de entrada a la oculta no llevan pesos asociados.
Linealidad en la capa de salida: en la RBFN es indispensable una función lineal, en tanto que en el MLP puede ser un axón simple.
Función de activación: la RBFN está compuesta de una función de Gauss y la MLP permite escoger la función que más se adecue.
Más investigación es necesaria para ofrecer resultados concluyentes, sólidos, que inviten a la reflexión con base en el análisis realizado, es posible el empleo de técnicas de nanotecnología [18, 19] para solidificar el proceso y robustecer la aportación a través de un análisis comparativo.
Agradecimientos
Los autores agradecen al IPN por el apoyo otorgado para la elaboración del presente trabajo, al CONACYT, la UAEH Campus Sahagún, las Universidades, Centros, y a todos y cada uno de los participantes/colaboradores que por razones de espacio no es posible detallar en éste documento y los cuales han brindado apoyo y soporte en la realización del presente proyecto de investigación.
Referencias
[1] Campos, L, M. Islas, G. Ramírez, C. VillaVelázquez, and C. Mota. "Growth kinetics of borided layers: Artificial neural network and least square approaches" en Coatings and Interfaces Symposium, XVI Internacional Materials Reserch Congress. Cancún, Quintana Roo, México, 2007
[2] Campos, L, M. Islas, G. Ramírez, C. VillaVelázquez, and C. Mota. "Growth kinetics of borided layers: Artificial neural network and least square approaches" in Applied Surface Science, Volume 253, Issue 14, 15 May 2007, Pager 6226-6231.
[3] Mota H. Cinthya I, Morales M. Oswaldo, Campos S. Ivan E., "Desarrollo de Redes Neuronales para determinar la tenacidad a la fractura por microindentación en aceros borurados" en Fracture Mechanics, XVI Internacional Materials Reserch Congress. Cancún, Quintana Roo, México, 2007
[4] Mota H. Cinthya I, Morales M. Oswaldo, Campos S. Ivan E. "Calculo del coeficiente de Tenacidad a la Fractura en Aceros Borurados, mediante Redes Neuronales Artificiales”. Memorias del 5º Congreso Internacional de Ingeniería Electromecánica y de Sistemas. Escuela Superior de Ingeniería Mecánica y Eléctrica. Instituto Politécnico Nacional. 2008.
[5] Mota H. Cinthya I, Morales M. Oswaldo, Campos S. Ivan E., Hernández S. Luis M. “Desarrollo de Redes Neuronales para determinar la tenacidad a la fractura por microindentación en aceros”. Memorias del 10º Congreso Nacional de Ingeniería Electromecánica y de Sistemas. Escuela Superior de Ingeniería Mecánica y Eléctrica. Instituto Politécnico Nacional. 2008.
[6] Giselle Ramírez Sandoval, “Caracterización De Grietas Auto-Afines En Capas Borurizadas Para Aceros Estructurales AISI 1045” Tesis de maestría, Instituto Politécnico Nacional, 2006.
[7] WINSTON, Patrick H., Inteligencia Artificial. 3ª ed., Addison-Wesley Iberoamericana, 1994., pp. 805.
[8] Manuel F. González Penedo, Redes de Base Radial. http://www.lfcia.org/~cipenedo/cursos/scx/archivospdf/Tema5-6.pdf.
[9] Manual Neurodimensión, Neurosolutions. http://www.nd.com. [ Links ]
[10] Russell Stuard & Norvig Peter, “Inteligencia Artificial: Un enfoque Moderno.” Pearson Education S.A., Prentice Hall, Hispanoamerica S.A., 2004, pp. 1240.
[11] S. Y. Kung, “Digital Neural Networks", 1993. PTR Prentice Hall, Inc.
[12] J. Anderson. A memory model using spatial correlation functions; pp. 113-119
[13] Martín Bonafio, “Redes neuronales y Sistemas Difusos”, Madrid, Ediciones Alfaomega, 2001, pp. 399.
[14] José R. Hilera y Víctor J Martínez, “Redes Neuronales Artificiales”, 2000. Alfaomega. Madrid. España, 2000, pp. 390.
[15] Montaño Moreno Juan José, “Redes Neuronales Artificiales aplicadas al Análisis de Datos”, Universitat De Les Illes Balears Facultad de Psicología, Palma De Mallorca, 2002 Tesis doctoral.
[16] Horacio Paggi, “Predicción de series de datos utilizando redes neuronales”, Montevidel Uruguay, 2003, Instituto De Computación, Universidad De La República, Tesis De Maestría.
[17] L. Almeida. A learning rule for asynchronous perceptrons with feedback in a combinatorial environment. Proceeding of the IEEE First International Conference of Neural Network. Vol. II pp. 609-618.
[18] Rodríguez-Castro, G., Campos-Silva, I., Chávez-Gutiérrez, E., Martinez-Trinidad, J., Hernandez-Sanchez, E., & Torres-Hernández, A., "Mechanical properties of FeB and Fe 2 B layers estimated by Berkovich nanoindentation on tool borided steel", Surface and Coatings Technology, 2013, vol. 215, pp. 291-299.
[19] Kulka, M., Makuch, N., Dziarski, P., & Piasecki, A., "A study of nanoindentation for mechanical characterization of chromium and nickel borides’ mixtures formed by laser boriding", Ceramics International, 2014, vol. 40, no 4, pp. 6083-6094.














