Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Acta Nova
On-line version ISSN 1683-0789
RevActaNova. vol.7 no.3 Cochabamba Mar. 2016
ARTÍCULO CIENTÍFICO
Construcción axiomática del conjunto de los números naturales a partir de una condición sobre su cardinalidad
Axiomatic construction of the set of natural numbers from a condition on its cardinality
Oscar R. Pino Ortiz1 y Zonia K. Morales Salomón2
1Universidad Católica Boliviana, Cochabamba, Bolivia
2Universidad Simón I. Patiño, Cochabamba, Bolivia
pino@ucbcba.edu.bo
Recibido: 8 de febrero 2016
Aceptado: 27 de febrero 2016
Resumen: Se construye la estructura algebraica de ![]() a partir de un conjunto de cardinalidad
a partir de un conjunto de cardinalidad ![]() 0. Como consecuencia el axioma de inducción de Peano se presenta como un teorema.
0. Como consecuencia el axioma de inducción de Peano se presenta como un teorema.
Palabras clave: Peano, Cantor, Números naturales, Inducción.
Abstract: The algebraic structure of ![]() is constructed from a set of cardinality
is constructed from a set of cardinality ![]() 0. As a result the induction Peano axiom is presented as a theorem.
0. As a result the induction Peano axiom is presented as a theorem.
Key words: Peano, Cantor, Natural numbers, Induction.
1. Introducción
Se dan por conocidas la Teoría Axiomática de Conjuntos, el Axioma de Elección y la Teoría de la Cardinalidad de Georg Cantor. Clásicamente ![]() es construido a partir de los axiomas de Giuseppe Peano. En el cuerpo del artículo se lo construirá utilizando una característica fundamental de
es construido a partir de los axiomas de Giuseppe Peano. En el cuerpo del artículo se lo construirá utilizando una característica fundamental de ![]() : su cardinalidad. En efecto
: su cardinalidad. En efecto ![]() es un conjunto infinito pero cuya cardinalidad es la más pequeña entre las cardinalidades de los conjuntos infinitos. La estructura algébrica de
es un conjunto infinito pero cuya cardinalidad es la más pequeña entre las cardinalidades de los conjuntos infinitos. La estructura algébrica de ![]() y, en particular, la inducción matemática que caracteriza esa estructura puede ser construida de manera formal a partir de este hecho, siempre que se dé por válido el axioma de elección.
y, en particular, la inducción matemática que caracteriza esa estructura puede ser construida de manera formal a partir de este hecho, siempre que se dé por válido el axioma de elección.
2. Generalidades
Definición 1. Conjunto infinito
Decimos que un conjunto A es infinito si tiene la misma cardinalidad que una de sus partes propias, es decir:
A es infinito

Φ: A → A inyectiva, no sobreyectiva.
Categoría de los Conjuntos
La clase de los conjuntos provisto de las aplicaciones como morñsmos es una categoría. Los objetos de esta categoría admiten un orden natural que notaremos ![]()
Definición 2.
Diremos que A ![]() B si es posible encontrar una aplicación inyectiva de A en B. Es decir:
B si es posible encontrar una aplicación inyectiva de A en B. Es decir:
A
B

γ:A→ B inyectiva.
Leeremos "A es más pequeño o igual a B ".
Diremos que A ≡ B si es posible encontrar una aplicación biyectiva de A en B. Es decir:
A ≡ B

γ: A → B biyectiva.
Observación
Es evidente que
A
A (reflexividad)
A
B y B
C
A
C (transitividad)
Mientras que la anti simetría A ![]() B y B
B y B ![]() A
A ![]() A ≡ B es el famoso Teorema de Cantor-Bernstein.
A ≡ B es el famoso Teorema de Cantor-Bernstein.
Definición 3. Conjunto infinito más pequeño
Sea A un conjunto infinito. Decimos que A es uno de los conjuntos infinitos más pequeños si ![]() B conjunto,
B conjunto, ![]() φ: A → B inyectiva.
φ: A → B inyectiva.
Llamemos ![]() a uno de los conjuntos infinitos más pequeños.
a uno de los conjuntos infinitos más pequeños.
Definición 4. Los números naturales
Los elementos del conjunto ![]() serán llamados "números naturales" aunque su naturaleza de números será establecida posteriormente una vez que se determine la estructura algébrica de
serán llamados "números naturales" aunque su naturaleza de números será establecida posteriormente una vez que se determine la estructura algébrica de ![]() .
.
Teorema 1.
X es un conjunto infinito ![]()
![]() φ: X → X inyectiva tal que Im(φ) = X {α}, con a ∈ X.
φ: X → X inyectiva tal que Im(φ) = X {α}, con a ∈ X.
Demostración.
(![]() ) Sea X un conjunto infinito y a ∈ X.
) Sea X un conjunto infinito y a ∈ X.
Mostremos previamente que si X es infinito, X {α} también lo es. En efecto, como X es infinito, existe α: X → X inyectiva, no sobreyectiva. Definamos β:X→ X por:
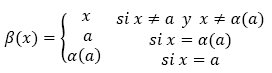
β es evidentemente biyectiva. Consideramos ahora la composición γ = β ° α: X → X. Está claro que γ(α) = α por lo tanto γ|x-{α} : X {α}→ X — {α} es inyectiva y no sobreyectiva. Concluimos que X {α} es infinito. Ambos conjuntos son de idéntica cardinalidad pues existe una biyección entre los dos, ya que la inclusión de X {α} en X es inyectiva y es posible construir una inyección de X en X {α} a partir de α: X > X. Para ello consideramos dos casos si α ![]() Im(a), en cuyo caso α:X → X {α} es inyectiva, y si α ∈ Im(a) definimos α':X → X — {α} por.
Im(a), en cuyo caso α:X → X {α} es inyectiva, y si α ∈ Im(a) definimos α':X → X — {α} por.
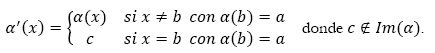
El teorema de Cantor-Bernstein garantiza la existencia de la biyección deseada.
En resumen: #X {α} = #X de donde ![]() δ: X → X {α} biyectiva.
δ: X → X {α} biyectiva.
Pero ![]() i: X {α} → X inyectiva (por ejemplo la inclusión)
i: X {α} → X inyectiva (por ejemplo la inclusión)
Si definimos φ = i ° δ:X → X, vemos que φes inyectiva y tal que
![]()
(![]() ) Como φ es inyectiva pero no sobreyectiva entonces X es infinito
) Como φ es inyectiva pero no sobreyectiva entonces X es infinito
Definición 5. Aplicación "sucesor"
Como ![]() es un conjunto infinito, por el anterior teorema podemos afirmar que existe una función
es un conjunto infinito, por el anterior teorema podemos afirmar que existe una función ![]() :
: ![]() →
→ ![]() inyectiva tal que Im(
inyectiva tal que Im(![]() ) =
) = ![]() {α}, con α ∈
{α}, con α ∈![]() ; a esta función
; a esta función ![]() , se la llamará función sucesora y al elemento α se le llamará cero y se lo denotará por el símbolo 0.
, se la llamará función sucesora y al elemento α se le llamará cero y se lo denotará por el símbolo 0.
Observación: Ya que ![]() es una aplicación inyectiva,
es una aplicación inyectiva, ![]() n ∈,
n ∈, ![]() ! m ∈
! m ∈ ![]() t.q.
t.q.![]() (n) = m, entonces diremos que todo número natural tiene un único sucesor. Pero por otra parte,
(n) = m, entonces diremos que todo número natural tiene un único sucesor. Pero por otra parte, ![]() no es sobreyectiva: Im(
no es sobreyectiva: Im(![]() ) =
) = ![]() {0}, entonces diremos que todo número natural tiene antecesor excepto el cero, es decir
{0}, entonces diremos que todo número natural tiene antecesor excepto el cero, es decir ![]() m ∈
m ∈ ![]() t.q.m ≠0,
t.q.m ≠0, ![]() n ∈ M t.q. la pre-imagen de m es n.
n ∈ M t.q. la pre-imagen de m es n.
Teorema 2. Inducción
Sea E⊂ ![]() tal que:
tal que:
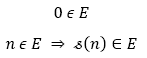
Entonces E = ![]()
Demostración:
E es infinito, en efecto:
Tomamos ![]() , donde
, donde ![]() es la función sucesora.
es la función sucesora.
0 ∈ E Pero 0 ![]()
![]() *(E) = Im(
*(E) = Im(![]() /E) , porque 0 no tiene antecesor.
/E) , porque 0 no tiene antecesor.
Por lo tanto ![]() /E no es sobreyectiva pero si inyectiva, entonces concluimos que E es infinito.
/E no es sobreyectiva pero si inyectiva, entonces concluimos que E es infinito.
Se mostrará que E = ![]() :
:
Como ![]() es uno de los conjuntos infinitos más pequeños
es uno de los conjuntos infinitos más pequeños ![]() φ:
φ: ![]() → E inyectiva.
→ E inyectiva.
Si 0 ![]() Im(φ) podemos fabricar una función inyectiva φ':
Im(φ) podemos fabricar una función inyectiva φ':![]() → E tal que 0 ∈ Im(φ') de la manera siguiente: Sea c ∈ Im(φ).
→ E tal que 0 ∈ Im(φ') de la manera siguiente: Sea c ∈ Im(φ).
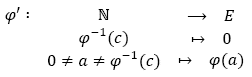
Supongamos entonces 0 ∈ Im(φ).
Construimos las siguientes funciones inyectivas:
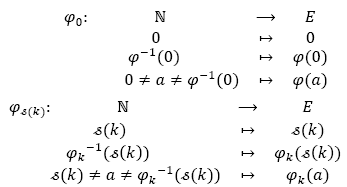
Donde k ∈ ![]()
Por otra parte, se define el siguiente conjunto: Fk = {n ∈ ![]() |n ≠ φk(n)} y notamos que F
|n ≠ φk(n)} y notamos que F![]() (k) ⊂ Fk , tomando F = ∩k∈
(k) ⊂ Fk , tomando F = ∩k∈![]() Fk, observamos que F = ø.
Fk, observamos que F = ø.
Por el Axioma de Elección entonces podemos construir la siguiente función biyectiva:
![]()
Donde ![]() = {φk|k ∈
= {φk|k ∈ ![]() } y
} y ![]() = {Fk|k ∈
= {Fk|k ∈ ![]() }. Observamos que a F le corresponde la función
}. Observamos que a F le corresponde la función ![]() que es la inclusión de
que es la inclusión de ![]() en E , por consiguiente
en E , por consiguiente ![]() ⊂ E. Pero como E ⊂
⊂ E. Pero como E ⊂ ![]() , entonces E =
, entonces E = ![]() .
.
Observación: Finalmente, estando dado que ![]() es tal que
es tal que
0 ∈ ![]()
![]() :
: ![]() →
→ ![]() {0} es biyectiva
{0} es biyectiva
Sea E ⊂ ![]() tal que:
tal que:
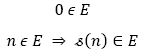
Entonces E = ![]()
Podemos dotarlo, de la manera clásica1, con la estructura algébrica que habitualmente tiene.
Notas
1 Con la adición y la multiplicación definidas por inducción.