ARTÍCULO CIENTÍFICO

 

Un operador de Sheffer en la Lógica IGR₃¹

 

A Sheffer operator in IGR₃-Logic

 

 

Oscar R. Pino Ortiz¹ y Zonia K. Morales Salomón²

¹Universidad Católica Boliviana, Cochabamba, Bolivia;
²Universidad Mayor de San Simón, Cochabamba, Bolivia
pino@ucbcba.edu.bo

Recibido: 20 de marzo 2015
Aceptado: 14 de abril 2015

 

 

---

Resumen: Una vez explicitado el nexo entre los operadores de una lógica p-multivaluada (p primo) y el anillo de polinomios Z_p[x,y], se demuestra de forma algébrica que la lógica a 3 valores IGR₃ admite como operador de tipo Sheffer al operador [x;y] = 1 + 2(x²y + xy²).

Palabras Clave: Lógica, Multivaluada, Sheffer, IGR

---

Abstract: Defined a functor from a p-multivalued logic (p prime) and the polynomial ring Z_p[x,y], it is demonstrated by algebraic arguments the existence of a Sheffer operator in the 3-valued logic IGR₃: [x; y] = 1 + 2(x²y + xy²).

Key words: Logic, Multivalued, Sheffer, IGR

---

 

 

1. Introducción

Desde hace ya tiempo, el establecimiento de una teoría coherente sobre una lógica con más de dos valores ha atraído la atención de algunos investigadores filósofos, matemáticos, o peritos de otras disciplinas en los que la lógica bivalente parecía insuficiente. Algunos intentos llegaron lejos (Lukasiewicz, Kleene, Post, Pierce, Chang).

En Bolivia, el Ing. Iván Guzmán de Rojas se ocupó en el estudio de la estructura matemática de la lengua aimara. Como resultado del acercamiento que realizó entre la lingüística y la formalización del razonamiento deductivo, Guzmán de Rojas estableció la existencia de un anillo algébrico relacionado con la lógica trivalente de ese idioma.

El hecho de poner en evidencia el uso de una lógica a tres valores en una lengua natural humana fue por sí solo sorprendente pues por lo general (según lo que sabemos) las lenguas occidentales se conforman con gramaticalizar la lógica bivalente que elimina la posibilidad de una ambigüedad incómoda, tomando la asignación de sólo dos alternativas para toda proposición dentro de una argumentación: verdadera o falsa. Ese el famoso principio del tercero excluido.

Según Guzmán de Rojas, la lengua aimara se estructuró de manera distinta, pues ha integrado plenamente en su gramática la duda como tercer valor lógico. El análisis de los sufijos gramaticales de la lengua andina (el aimara es una lengua aglutinante) es suficiente para convencerse de ello, como lo demuestra el mencionado científico boliviano.

Ciertamente no es fácil, para quien razona apoyándose en el principio del tercero excluido, entender las inferencias que admiten la duda como parte integrante del pensamiento deductivo.

Este artículo no pretende hacer un paralelo entre el aimara y las lenguas occidentales, sino simplemente formalizar algunos aspectos de la lógica trivalente, sin referencia directa al idioma aimara, y extender la estructura de la misma a unas lógicas multivaluadas que vamos a llamar lógicas IGRp, como un reconocimiento para quien inició la investigación sobre esta apasionante teoría.

 

2. Generalidades

Los valores lógicos 0 y 1, provistos de las operaciones + y • , forman lo que se llama comúnmente el cuerpo o campo conmutativo Z₂.

En la lógica trivalente, es bien conocido que los conectivos posibles (operadores binarios) no son 16, ni los operadores unarios 4, como lo son en la lógica bivalente, sino pasan a ser 19683, mientras que los operadores unarios pasan a ser 27.

Hace unos cincuenta años atrás, Lukasiewicz² basándose en una elección intuitiva pero arbitraria, con la voluntad de "extender" la lógica bivalente a una trivalente que de cierta manera contenga a la primera, definió un operador binario que cumplía la función de la implicación. Al hacerlo, encontró que no todos los teoremas lógicos clásicos permanecían válidos. Si bien, era razonable que el principio del tercero excluido desaparezca, parecía perjudicial que el modus ponens o la transitividad de la implicación resulten inválidas.

Posteriormente numerosos matemáticos abundaron en propuestas alternativas pero siempre con resultados aparentemente insatisfactorios. Lo que sí salió a la luz, de forma inequívoca, fue el hecho de que en todos los intentos se hacía una elección que pese a todo se sentía arbitraria.

La pregunta que nos planteamos entonces es la siguiente:

¿Existe una manera natural de extender la lógica bivalente en una trivalente?

El valor de la investigación de Iván Guzmán de Rojas reside en la respuesta que da a esa pregunta:

Sí, existe una forma natural de encarar esa extensión y la clave se encuentra en la lengua aimara y en particular en el aimara siwi³.

Como punto de referencia, recordemos que Chang⁴, en un intento de formalizar los trabajos de Lukasiewicz, definió una extensión estructurada de la lógica bivalente a una polivalente: la MV-álgebra, una lógica n-valuada, con n un número natural cualquiera. En el trabajo que exponemos a continuación, fue menester restringir n, para tomar sólo los números primos p. Esta restricción se origina en el hecho de que existe una biyección natural entre los operadores unarios del conjunto que llamamos lógica IGR_p y los polinomios a una variable a coeficientes en el cuerpo Z_p, y otra biyección, igualmente natural, entre los operadores binarios de la lógica IGR_p y los polinomios a dos variables a coeficientes en el cuerpo Z_p. La demostración de este hecho desarrollada a continuación, se sustenta en algunos resultados de los matemáticos europeos Alejandro Teófilo Vandermonde (1735-1796) y Leopoldo Kronecker (1823-1891)⁵.

La principal consecuencia, resultado que justifica por sí solo el trabajo realizado, es que ahora sabemos de que es posible "razonar" con una lógica multivaluada de manera totalmente similar a lo habitual con una bivaluada siendo posible comprender un sistema de proposiciones con p valores lógicos de una manera equivalente a la de resolver un sistema de ecuaciones en un anillo de polinomios.

 

3. Remembranza Técnica

Como se mencionó anteriormente, algunos investigadores (Kleene, Lukasiewicz, Pierce) propusieron extensiones trivalentes para ciertos conectivos lógicos. Kleene, por ejemplo propuso las siguientes:

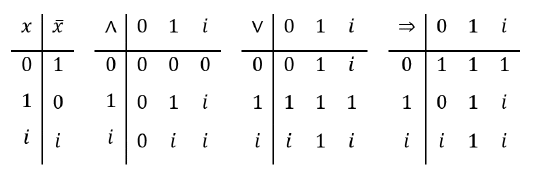
Las cuales definen la negación, la conjunción, la disyunción y la implicación. El valor i es obviamente el tercer valor lógico. Esta extensión se basó en la intuición del autor y las consideraciones consecuentes del estudio efectuado por Lukasiewicz.

Posteriormente, Chang estructuró la propuesta de Lukasiewicz dando lugar a una teoría formal: las MV-álgebras.

Una MV-álgebra es una estructura (M, , 0) cuya base es un monoide conmutativo al que se le imponen las condiciones adicionales:

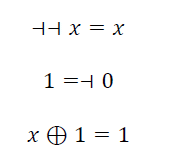
Todas las propuestas de extensión de la lógica bivalente en una trivalente, encontraron ciertas aparentes dificultades para comprender el hecho de que, en algunos casos, el silogismo modus ponens se invalida y, en otros, la transitividad de la implicación no es una tautología. Para salvar el problema se puso incluso en tela de juicio el concepto de tautología y el de contradicción.

El verdadero problema era el de saber cuáles propiedades conservar y cuáles desechar. Es decir el de encontrar una manera natural para definir la extensión deseada, pues, sin la cualidad de naturalidad, se tenía la tentación de atribuir las incoherencias a una mala elección de los conectivos elegidos para emprender la extensión.

Guzmán de Rojas, al estudiar el idioma aymara, observó que esta lengua había incorporado a su estructura una lógica trivalente basada en tres valores, -1=falso, 0=dudoso y 1=verdadero, la cual utilizaba los conectivos:

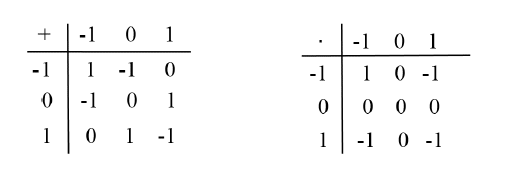
El lector ha seguramente reconocido la adición y multiplicación del anillo Z₃.

La naturalidad de una lógica basada en este anillo comenzaba a ser evidente⁶. Guzmán de Rojas observó que los operadores binarios de la lógica trivalente aymara se construyen en base a los operadores unarios de la siguiente manera:

Donde p, q y r son operadores unarios, + la adición en Z₃ y k el operador binario definido en base a aquellos. De este hecho, Guzmán de Rojas dedujo que existe una relación estrecha entre los operadores binarios y los polinomios a dos variables del tipo:

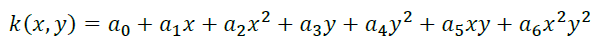
con a_¡ un elemento de Z₃. Esto le permitió afirmar que la resolución de los problemas inferenciales en una lógica trivalente se puede obtener por métodos puramente algebraicos. Pero con sólo ese tipo de polinomios la sugerencia de Guzmán de Rojas no establecía una biyección entre operadores y polinomios.

Para obtener tal biyección era preciso "extender" la idea de Guzmán de Rojas asociando a todo operador binario un polinomio a coeficientes en Z₃ del tipo:

Lo que realmente establece una biyección entre ambos conjuntos (operadores y polinomios). En efecto a la operación binaria.

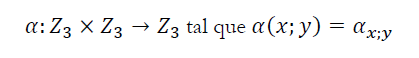
asociamos el polinomio:

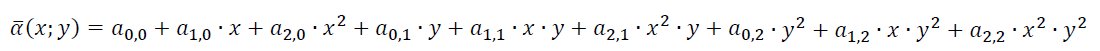
Cuyos coeficientes a_i,j se encuentran como resultado de la aplicación de una "matriz de traspaso" 0₃ al vector formado por los valores α_i;j colocados en el orden i + j • p.

La demostración de la biyectividad pasa, está claro, por el cálculo del determinante de una matriz. En nuestro caso el de la matriz descrita a continuación:

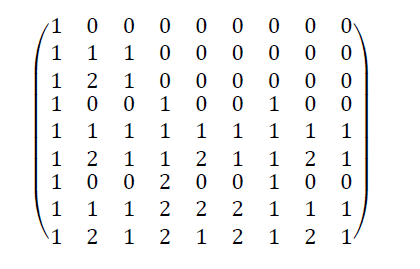
que es la matriz que asocia a cada polinomio un operador binario, la cual no es otra cosa que el producto de Kronecker

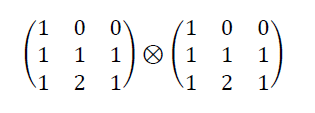
Observamos   además que cada uno de los factores es la matriz de Vandermonde módulo 3.

Hecha dicha corrección, la tentación inmediata fue la de extender la lógica trivalente (y por ende la bivalente) en una polivalente que conservase la flexibilidad y naturalidad de la lógica IGR₃. Satisfacer esta tentación (es decir, establecer el carácter functorial de la correspondencia) fue posible gracias a los resultados establecidos por el matemático alemán Kronecker en el área del cálculo tensorial.

Así pues, pudimos asociar a cada operador binario de una lógica a p valores (con p primo) un polinomio a dos variables y a coeficientes en Z_p. La imposición "p primo" viene de la necesidad de trabajar sobre un campo conmutativo. El polinomio asociado es

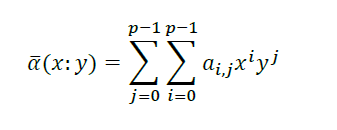
La matriz de traspaso 0_p será la inversa del producto:

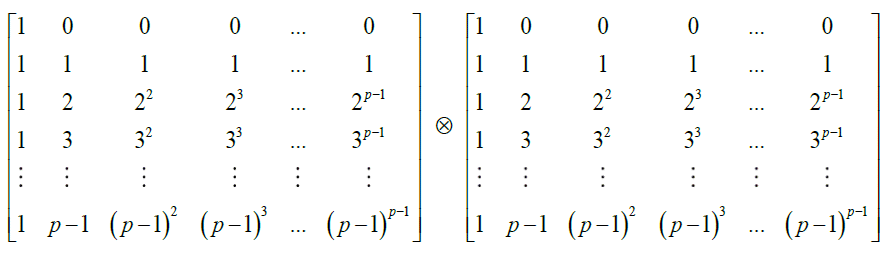
La matriz 0_p existe pues, es la inversa de un producto de Kronecker (correspondiente del producto tensorial de las aplicaciones lineales asociadas) de dos matrices de Vandermonde. Se establece que su determinante es no nulo mediante la fórmula

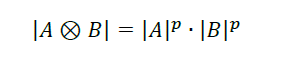
Es más: 0_p no es otra cosa que el producto de Kronecker

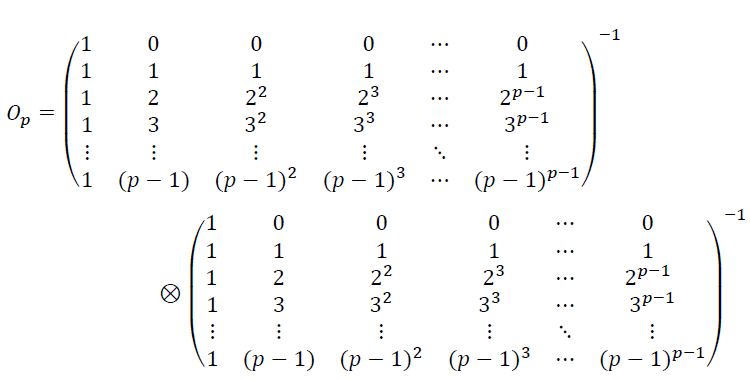
Lo que demuestra la biyectividad de la correspondencia establecida. Queda así abierto un camino natural para el estudio de las lógicas multivaluadas y, sobre todo, para la resolución de un sistema lógico p-multivaluado a través de la resolución de un sistema de ecuaciones polinomiales a coeficientes en Z_p. Esta última tarea es ardua para un humano, pero no para una computadora. Por ello apostamos por una aplicación benéfica a los sistemas expertos.

 

4. El criterio de Slupeki

Un problema, que ha sido sujeto de interés para los matemáticos dedicados al estudio de la Lógica, es el de determinar si un conjunto de operadores, en una lógica dada, es o no funcionalmente completo.

En una lógica proposicional trivaluada existen 19683 operadores lógicos, a diferencia de la lógica bivaluada, en la que existen tan sólo 16 operadores binarios y 4 unarios. El intento de ir probando, uno a uno, todos los conjuntos de operadores posibles de una lógica trivaluada, hasta hallar uno que sea funcionalmente completo, requiere mucho tiempo. Incluso si escogemos un conjunto al azar, probar que es funcionalmente completo de manera "manual" es entrar en una labor tediosa y prolongada que además contiene una alta probabilidad de fracaso. De ahí que es menester llegar a una generalización de los criterios de un conjunto que sea funcionalmente completo. Uno de los teoremas más útiles para esto es el criterio de Slupecki:

Teorema de Slupeki ([Síupeki, 1939]). Sea m ≥ 2, m є . Si F es un conjunto de operadores lógicos a m valores, que contiene todos los operadores unarios y al menos una función esencial⁷ entonces F es funcionalmente completo.⁸

Nuestro objetivo ahora es encontrar un operador de tipo Sheffer en la lógica IGR₃, es decir encontrar un operador tal que todo conjunto que lo contenga sea funcionalmente completo.

Gracias a la biyección establecida entre los operadores de la lógica IGR₃ y los polinomios en ₃[x;y], es posible adoptar un enfoque algebraico. Evidentemente utilizaremos como apoyo el criterio de Slupecki. Sin embargo, la demostración que se plantearemos será independiente del criterio de Slupecki, ya que pretendemos dar un sentido totalmente algebraico a este problema típico de la lógica, obteniendo un tratamiento conceptualmente más simple que el habitual en el cálculo proposicional.

A continuación, traduciremos el planteamiento del problema propuesto a un lenguaje algebraico.

 

5. Tratamiento algebraico del problema

Sea K₀ = K[x₁ ,...,x_n] un anillo de polinomios, con K un cuerpo y sea F K₀

Definición 1: Sea p є K₀, se dice que p es construible con F, si se cumple alguna de las siguientes condiciones:

1. p = x_i

2. p = p₀(p₁ ,...,p_m) tal que p_i є F o p_i es construible con F

Nota: Como puede observarse la definición anterior es recursiva

Definición 2: Se dice que A K₀ es una construcción polinomial, si todos los elementos construibles con A, pertenecen a A.

Remarca: K₀ es una construcción polinomial porque, por definición, una construcción polinomial es un subconjunto de K₀, entonces de manera necesaria todos los elementos construibles con K₀ tienen que pertenecer a K₀

Definición 3: Sea B K₀, la clausura polinomial de B, es la construcción polinomial más pequeña que contiene B. Es equivalente a definir la clausura polinomial como⁹:

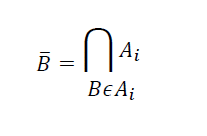
Donde A_i es una construcción polinomial.

Definición 4: Sean A, B K₀, si = A se dice que B genera a A

Definición 5: Se dice que una construcción polinomial A es principal si p є A tal que = A, es decir que {p} genera A

Proposición 1: Sea K₀ , si los elementos de K₀ son construibles por , entonces genera a K₀.

Demostración: K₀ es una construcción polinomial por la remarca de la definición 2, y es la construcción polinomial más pequeña que contiene a , si existiera una construcción polinomial B K₀ que contiene a , necesariamente existiría por lo menos un p є {K₀\B] que no es construible con B. Como p є K₀ , entonces p es construible por , por lo tanto p є B, llegando a un absurdo. Se concluye entonces que = K₀. Es decir, que {} genera a K₀.

Observación:

El problema de encontrar un operador de tipo Sheffer en IGR₃, se traduce en mostrar que ₃[x; y] es principal, es decir que existe un polinomio p є ₃[x; y] tal que {p} genere a ₃[x; y].

 

Resolución del problema

1.1 Proposición 2: Sean p,q є ₃ [x; y]. Entonces el conjunto {1, p • q, p + q} ₃ [x; y] genera a ₃ [p; q]

Demostración:

Primero se mostrará que todos los polinomios de ₃ [p; q] son construibles por {1, p • q, p + q}. Se sabe que cualquier polinomio de ₃[p; q] tiene la siguiente forma:

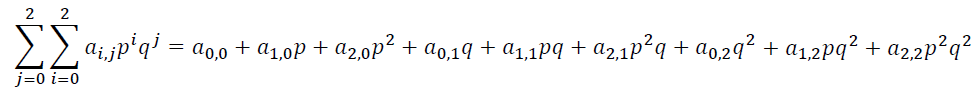
A mostrar que ∑²_j=0∑²_i=0= a_i,jpⁱq^j construible con {1, p • q, p + q}. En efecto:

Denotemos por p₀ = 1; p₁ = p • q ; p₂ = p + q:

•    p₂(p₀, p₀) = 1 + 1 = 2

•    p₂(p₀, 2) = 2 + 1 = 0

•    Como 0, 1 y 2 son construibles, a_i,j є ₃ es construible.

•   p₁(a_1,0,p) =a_1,0p / las variables del anillo de polinomios son construibles por la definición 4, en este caso el anillo de polinomios es ₃ [p; q], y las variables p y q

•    p₁(p, p)=p²

•   v(q, q) = q²

•    p₁(a_2,0, p²) = a_2,0p²

•    p₁(a_0,1,q) = a_0,1q

•   p₁(a_1,1, p) = a_1,1,p

•    p₁(a_1,1p, q) = a_1,1, pq

•    p₁(a_2,1, p²) = a_2,1p²

•    p₁(a_2,1p², q) = a_2,1p²q

•    p₁(a_0,2, q²) = a_0,2q²

•    p₁(a_1,2, p) = a_1,2p

•    p₁(a_1,2p, q²) = a_1,2pq²

•    p₁(a_2,2, p²) = a_2,2p²

•    p₁(a_2,2p²,q²) = a_2,2p²q²

Sumamos por medio del polinomio p₂ = p + q, los polinomios que se mostraron construibles: a_0,0, a_1,0p, a_2,0p², a_0,1q, a_1,1pq, a_2,1p²q, a_0,2q²,a_1,2pq²,a_2,2p²q² obteniendo:

Por lo tanto, se concluye que todos los elementos de ₃[p; q] son construibles con {1, p + q, p.q} y por la proposición 1 deducimos que {1, p + q, p . q} genera a ₃[p; q].

Remarca: Si sustituimos a p = x y q = y, se concluye que {1, x + y ,x • y} genera a ₃[x;y].

1.2 Proposición 3: {1 + 2x²y + 2xy²} genera a ₃ [x; y]

Demostración:

Denotamos por [x; y] = 1 + 2x²y + 2xy^{2 (10)} Previo a la demostración, se mostrarán unas propiedades del polinomio [x; y]:

Propiedad 1: Sea p є ₃[x; y], [p; p] = 1 + p. En efecto ¹¹:

[p; p] = 1 + 2p²p + 2pp² = 1 + 2p + 2p = 1+ p

Propiedad 2: Sea p є ₃ [x; y] construible con [x; y] entonces 1 + p, 2 + p son construibles con [x; y].

En efecto:

Por la propiedad 1, [p; p] = 1 + p , de donde 1 + p es construible con [x; y].

Por la propiedad 1, [p + 1; p + 1] = 1 + 1 + p = 2 + p, de donde, 2 + p es construible con [x; y].

Para la demostración de la proposición, probaremos los siguientes incisos:

i) Sea p є ₃[x;y] construible con [x;y], entonces, los elementos de ₃[p] = {a₀ + a₁p + a₂p | a_i є ₃} son construibles con [x; y].

Existen 27 posibles polinomios de esta forma, que son construibles con {[x;y]}, en efecto:

-     Por condición, p es construible, por lo tanto p + 1 y p + 2 son construibles con [x; y] (por la propiedad 2).

-     [1 + p; p] = 1 + 2(1 + p)²p + 2(1 + p)p² = 1 + 2p(1 + 2p + p²) + 2p²(1 + p) = 1 + 2p + p² + 2p + 2p² + 2p = 1 . Entonces los polinomios 2 y 0 son construibles con [x; y] (por la propiedad 2)

-     [p; 1] = 1 + 2p² + 2p. Por lo que, 2 + 2p² + 2p y 2p² + 2p son construibles con [x;y] (por la propiedad 2)

-     [p; 2] = 1 + p² + 2p. De donde, 2 + p² + 2p y p² + 2p también son construibles con [x;y] (por la propiedad 2)

-     [p + 1,1] = 1 + 2(p + 1)² + 2(p + 1) = 1 + 2(p² + 2p + 1) + 2p + 2 = 1 + 2p² + p + 2 + 2p + 2 = 2 + 2p². Entonces 2p² y 2p² + 1 es construible con [x;y] (por la propiedad 2)

-     [p + 1,2] = 1 + (p + 1)² + 2(p + 1) = 1 + p² + 2p + 1 + 2p + 2 = 1 + p + p². Por lo tanto, 2 + p + p² y p + p² son construibles con [x;y] (por la propiedad 2)

-     [p + 2,1] = 1 + 2(p + 2)² + 2(2 + p) = 1 + 2(1 + p + p²) + 1 + 2p = 1 + 2 + 2p + 2p² + 1 + 2p = 1+p + 2p². Entonces, 2 + p + 2p² y p + 2p² son construibles con [x;y] (por la propiedad 2)

-     [p + 2,2] = 1 + (p + 2)² + 2(2 + p) = 1 + (1 + p + p²) + 1 + 2p = p². Entonces p² + 1, p² + 2 son construibles con [x;y] (por la propiedad 2)

-     Ya se mostró que 1 + p², 1 + p + 2p² son construibles con [x;y], de donde [1 + p²,1 + p + 2p²] = 1 + 2(1 + p²)²(1 + p + 2p²) + 2(1 + p²)(1 + p + 2p²)² = 1 + 2(1 + p + 2p²) + 2(1 + p²) = 1 + 2 + 2p + p² + 2 + 2p² = 2 + 2p es construible con [x;y], por lo tanto 2p y 2p + 1 son construibles con [x;y].

Remarca: Ya que x є ₃[x;y] es construible con [x;y] por ser variable, sustituimos p = x, mostrando que los elementos de ₃[x] son construibles con [x;y]. Los elementos de ₃[x] equivalen a los operadores unarios en IGR₃.

Ahora mostremos que los polinomios a dos variables son construibles con [x;y].

ii) El polinomio p = 1 es construible con [x;y]

El polinomio p = 1 є ₃[x] y en el inciso i) se mostró que {1 + 2x²y + 2xy²} genera a ₃[x], por lo tanto, todos sus elementos son construibles con {1 + 2x²y + 2xy²} incluyendo el polinomio p = 1.

iii) Sean p,q є ₃[x;y] construibles con [x;y], entonces el polinomio p • q es construible con [x; y].

Previo a la demostración:

Lema 1: Sean p, q є ₃[x], tales que p² = p y q² = q , entonces [p; q] = 1 + pq.

Demostración:

[p; q] = 1 + 2p²q + 2pq² = 1 + 2pq + 2pq = 1 + pq

Notar que si p, q є ₃[x] tales que p² = p y q² = q son construibles con [x;y], entonces [p; q] = 1 + pq, es construible con [x;y].

Lema 2: Sean p, q є ₃[x], tales que p² = 1 y q² = 1 entonces

[p; q] = 1 + 2(p+q)

Demostración del lema 2:

[p; q] = 1 + 2p²q + 2pq² = 1 + 2q + 2p = 1 + 2(p + q)

Notar que si p, q є ₃[x] tales que p² = 1 y q² = 1 son construibles con [x; y], entonces [p; q] = 1 + 2(p + q), es construible con [x; y].

Demostración de iii)

p y q es construible / por condición

p² y q² es construible con {[x; y]} / por i)

r = 1 + (pq)² es construible / por el lema 1, ya que (p²)² = p² y (q²)² = q²

[p, q] = 1 + 2p²q + 2pq² es construible / por definición

=> 2p²q + 2pq² es construible / por la propiedad 2

=> [2p²q + 2pq²] es construible / por i)

=> (2p²q + 2pq²)² = 2pq + 2p²q² es construible

=> s = 2 + 2pq + 2p²q² es construible /por la propiedad 2

Observamos que r² = 1 y s² = 1, en efecto:

r² = (1 + (pq)²)² = 1 + 2(pq)² + (pq)² = 1

s² = (1 + 2pq + 2p²q² )² = 1 + p²q² + p²q² + pq + p²q² + 2pq = 1

=> 1 + 2 (r + s) es construible / por el lema 2

Pero 1 + 2(r + s) = 1 + 2(1 + (pq)² + 2 + 2pq + 2p²q²) = 1 + 2(2pq) = 1 + pq y entonces pq es construible con [x; y] por la propiedad 2.

pq es construible con [x; y].

Remarca: Sustituyendo p = x y q = y,se concluye que x • y es construible con{[x;y]}.

iv) Si p, q є ₃ [x; y] son construibles entonces el polinomio p + q es construible con [x; y]. En efecto:

Sean r, s, t є ₃[x; y], polinomios construibles con {[x; y]}

t • s es construible / por el inciso iii)

1 + t • s es construible / por la propiedad 2

t • (1 + t • s) es construible / por el inciso iii)

Tomamos t = 1 + r² que es construible por el inciso i), que tiene la propiedad que t = 1, de donde:

t • (1 + t • s) = (1 + r²)(1 + (1 + r²) • s) = (1 + r²) + (1 + r²)²s = 1 + r² + s es construible con [x; y].

Tomamos ahora r = 2p² + p , s = 2 + p² + q que son construibles con [x;y], por las consideraciones precedentes y sustituyendo en 1 + r² + s, se obtiene:

1 + r² + s = 1 + (2p² + p)² + 2 + p² + q = 1 + 2p²+p + 2 + p² + q = p + q

Entonces p + q es construible con [x; y].

Remarca: Sustituyendo p = x y q = y, se concluye que x + y es construible con [x; y].

Resumiendo, tenemos que los elementos de ₃ [x; y] son construibles con {1, x + y, x • y} (por la proposición 2), por otra parte, los elementos de {1, x + y, x • y}, son construibles con [x; y] (como se mostró en los incisos ii), iii) y iv)). Por lo tanto, los elementos de ₃[x; y] son construibles con [x; y], por medio de la proposición 1, se concluye entonces que [x; y] genera a ₃[x; y].

1.2.1 Corolario: ₃ [x; y] es principal

Un operador de tipo Sheffer para la lógica IGR₃

₃ [x; y] es principal en el sentido definido precedentemente, es decir se encontró un polinomio p = 1 + 2x²y + 2xy² tal que {1 + 2x²y + 2xy²} genera a ₃[x;y], esto quiere decir que, con tan sólo este polinomio, se construyen por evaluaciones sucesivas los 19683 polinomios que existen en ₃[x;y].

Gracias a la biyección entre ₃[x;y] y IGR₃ se puede encontrar la pre-imagen de este polinomio, que será el operador de tipo Sheffer para la lógica IGR₃. Este resultado cierra el problema que nos planteamos al inicio del presente artículo.

 

Notas

¹ Llamada así en honor del científico boliviano Iván Guzmán de Rojas quien estableció que el idioma aimara la integra de forma natural en su gramática.

² (Indicaciones biográficas sobre Lukasiewicz)

³ Z₃

⁴ (Nota biográfica de Chang)

⁵ (Nota biográfica sobre Vandermonde y Kronecker)

⁶ Nos ha sorprendido constatar que la lengua aimara (o su constructor, si acaso nos inclinamos a pensar que se trata de una lengua construida) incorpora el manejo del grupo S₃, pues los sufijos wa, ka, ti, kati, titi y tika, se combinan siguiendo la ley de composición de ese grupo (o más bien forman un grupo isomorfo a S₃).

⁷ Una función, de una lógica proposicional m-valuada, es esencial si es un operador a m valores que depende de al menos dos variables.

⁸ Una demostración de este teorema se encuentra en Urquhart, 2001.

⁹ La intersección finita de construcciones polinomiales es una construcción polinomial

¹⁰ Caso para p = 3 del polinomio definido por Pino para Z_p [x, y] : [x, y] = 1 + (p - 1) x^ky^p-k

¹¹ Aquí se utiliza el pequeño teorema de Fermat (Sea a є , p un número primo, entonces a^p = a (mod p)), en particular a³ ≡ a (mod 3). Si multiplicamos esta congruencia por a se obtiene a⁴ ≡ a² (mod 3), en general para las potencias pares a^2k = a² (mod 3).

 

6. Bibliografía

[1] Bochvar, D. (1937). On a Three-valued Logical Calculus and its Application to the Analysis of the Paradoxes of the Classical Extended Functional Calculus, trad.; M. Bergmann, Darthmount College, Hanover, New Hmapshire, 1980, U.S.A.

[2] Guzmán de Rojas, I. (2007). Logica Aymara y Futurología. La Paz: Editorial Santín.         [ Links ]

[3] Karpenko, A. (2006). Łukasiewicks logics and prime numbers. Moscow: Luniver Press.         [ Links ]

[4] Kleene, S. (1938). On notation for ordinal numbers. The Journal of Symbolic Logic, Vol. 3, No. 4, pp-150-155. Recuperado de: http://www.jstor.org/stable/2267778

[5] Łukasiewicz, J. (1975). Estudios de Lógica y Filosofía, selec y trad.; A. Deaño, Biblioteca Rev. Occ., Madrid.

[6] Miguel Cárdenas, M. (2006). Lukasiewicz: su lógica y su filosofía. (Tesis inédita de licenciatura). Universidad Autónoma Metropolitana, Mexico, D.F.

[7] J J O'Connor & E F Robertson (2001). Emil Leon Post. Mac tutor: History of mathematics. Recuperado de http://www-history.mcs.st-andrews.ac.uk/Biographies/Post.html.

[8] J J O'Connor & E F Robertson (2000). Jan Lukasiewicz. Mac tutor: History of mathematics. Recuperado de http://www-history.mcs.st-andrews.ac.uk/Biographies/Lukasiewicz.html.

[9] Pino, O. (2011-2012), Las Lógicas IGRp. Tarija.         [ Links ]

[10] Post, E. (1921). Introduction to a General Theory of Elementary Propositions. Americal Jurnal of mathematics, Vol. 43, No. 3, pp.163-185. Recuperado de http://www.jstor.org/stable/2370324

[11] Urquhart, A. (2001). Basic Many-valued Logic. Handbook of philosophical logic, 2nd Ed., Vol. 2, pp.249-295. Recuperado de http://www.academia.edu/1399119/Basic_many-valued_logic         [ Links ]

[12] Urquhart, A. (2008). Emil Post. Handbook of the History of Logic. Vol. 5: Logic form Rusell to Church, pp.1-50.         [ Links ]

[13] Velarde, J. (1978). Lógica Polivalente. El basilisco, nº 1. Pp.93-99. Recuperado de http://fgbueno.es/bas/bas10110.htm

[14] Wajsberg, M. (1977). Axiomatization of the three-valued calculus. Logical Works, pp. 12-29. Ossolineum, Wroclaw.         [ Links ]