Aplicación de ecuaciones diferenciales parciales a problemas de transferencia de calor

 

 

David Amurrio D.

Universidad Católica Boliviana, Pq. J. Trigo s/n Cochabamba, Bolivia

amurrio@ucbcba.edu.bo

 

 

---

Los grandes paradigmas que sustentan y delimitan las diferentes áreas del quehacer humano no son eternos. Lentamente, a lo largo de los años de actividad profesional podemos percibir como estos se mueven, casi imperceptiblemente, cediendo ante las fuerzas creadas por el desarrollo del conocimiento y la emergencia de nuevas necesidades. Ocasionalmente, tenemos la fortuna de ser testigos del colapso estrepitoso de algún paradigma y su reposición por otros que redefinen así nuestros campos de acción y nos obligan a modificar la curricula de nuestros estudiantes. La transferencia de calor, discutida ya por los antiguos (Heráclito circa. 500 a.c.) y “cheville ouvrière” de la revolución industrial atraviesa ahora tiempos de cambio. Temas como la crisis energética que se avecina, la integración de procesos, el calentamiento global y la necesidad de mayor eficiencia energética son algunos de los temas que deberán afrontar nuestros futuros ingenieros.

En su concepción moderna, la transferencia de calor se inicia hace 200 años [3] atrás cuando Jean Baptiste Joseph Fourier presentaba ante el Institut National en Paris sus primeros resultados sobre la propagación del calor en cuerpos sólidos[1].  Esquivando las complicadas polémicas  reinantes en su tiempo sobre la naturaleza del calor, Fourier desarrolló su tesis sobre la propagación del calor en cuerpos sólidos. Para poder desarrollar su planteamiento, tuvo que crear una original herramienta matemática que le permitiese resolver las dificultades y explorar los alcances e implicaciones de su teoría. En su exposición, Fourier aplicó su método a problemas de flujo de calor en estado estacionario y no estacionario, resolviendo problemas de transferencia de calor en cuerpos sencillos como una esfera, un cilindro y una pared. Pasados 2 siglos de su presentación inicial, estudiantes, científicos e ingenieros se encuentran todavía limitados a resolver analíticamente problemas de transferencia de calor en ..... una esfera, un cilindro y una pared.

El escaso progreso observado se debe a que las ecuaciones que describen el flujo de calor son ecuaciones diferenciales parciales, área poco estudiada en la curricula de los ingenieros [5]. Considerando los planteamientos básicos para conducción de calor en un cuerpo en estado estacionario (eq 1), y no estacionario (eq. 2), encontramos que soluciones analíticas son accesibles solo en unos cuantos casos. Descomponer el planteamiento inicial en series (técnica desarrollada por el mismo Fourier) o adoptar métodos numéricos implican procedimientos tediosos que finalmente son hasta irrelevantes por las posibilidades tan limitadas que tienen. Problemas reales de conducción de calor en cuerpos tridimensionales donde además intervienen consideraciones en la frontera y se inmiscuyen fenómenos de convección de calor y de radiación amén de cambios de fase y generación de calor, nunca han podido ser abordados de forma satisfactoria.

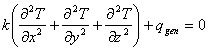                                                        [1]

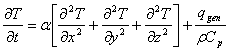                                                   [2]

Nos encontramos ahora en un momento de transición. El formidable desarrollo en técnicas de cómputo que ha marcado estos últimos 40 años nos ha llevado a un punto en el cual podemos empezar a arrancar a las ecuaciones en derivadas parciales de la oscuridad a la que fueron relegadas. Remontando nuestras miradas a tiempos pasados, podemos constatar cómo, los 300 años de reinado de la regla de cálculo, fueron abruptamente terminados con la aparición en la década de los 70 de la calculadora electrónica que banalizó los cálculos de logaritmos y funciones trigonométricas. La década de los 80 marcó la aparición de la computadora personal acompañada por la aplicación práctica de métodos numéricos y la posibilidad de resolver modelos matemáticos más complejos. En la década de los 90' se constató que los recursos de cómputo eran cada vez más poderosos y veloces, técnicas como las de Runge-Kutta para la resolución de sistemas de ecuaciones diferenciales ordinarias pasaron a formar parte de la curricula de los estudiantes de ingeniería. La pasada década ha visto la aparición de varios programas útiles para la resolución de problemas de ecuaciones diferenciales parciales y el consecuente desafío de encontrar la mejor manera de integrarlos en la curricula.

 

 

Método numérico con Matlab^®

Problemas de ecuaciones diferenciales parciales pueden ser planteados y resueltos con Matlab gracias a su herramienta pdetool [6]. Aspectos resaltantes del programa serán brevemente descritos a continuación, pudiendo el interesado referirse a los manuales para mayor detalle.

El programa se abre al escribir pdetool en la página principal de matlab, resultando en la apertura de un GUI PDE Toolbox (se sugiere seleccionar la opción de Heat Transfer en lugar del Generic Scalar que aparece en la parte superior). El objeto a través del cual se desea conducir calor tiene que ser dibujado a escala (seleccionar Draw Mode en la pestaña Draw) optando entre los botones marcados con un rectángulo, una elipse y un polígono los cuales combinados de manera inclusiva (signo +) o exclusiva (signo -) en el espacio marcado Set formula terminan por reproducir el objeto deseado.

Pasando enseguida a la pestaña marcada Boundary (seleccionar Boundary mode), seleccionar sucesivamente cada borde y definir su estado respectivo.

Las condiciones en la frontera ya pueden ser de tipo, Dirichlet con temperaturas fijas o indeterminadas para paredes aisladas:

                                                          [3]

O bien pueden corresponder a condiciones de tipo Neumann, en el cual el flujo de calor está determinado por condiciones externas:

                                                    [4]

Adoptando la nomenclatura del programa, se deberá introducir el valor de temperatura externa multiplicado por la constante convectiva en g y el valor de la constante convectiva h en lugar de q.

Para definir las condiciones al interior del objeto se debe seleccionar la pestaña marcada PDE y luego optar por PDE Specification, optando luego por un sistema de ecuaciones diferenciales parciales de tipo elíptico (estado estacionario):

                                                  [5]

Siendo esta última ecuación idéntica a la ecuación [1] (el valor de h siendo nulo).

Para el estado no estacionario se optará por el tipo parabólico:

                                 [6]

Siendo ésta última ecuación idéntica que la ecuación [2] (el valor de h siendo nulo)

La malla de elementos finitos se crea pulsando el botón Mesh y optando por Mesh Mode y finalmente el problema se resuelve pulsando el botón Solve ( en el caso del estado no estacionario se anotará antes los valores iniciales de temperatura por medio de la opción Parameters bajo el mismo botón de Solve).

Las temperaturas que corresponden a la solución del problema aparecen codificadas por color, pudiendo añadirse opciones interesantes como las curvas de isotermas, líneas de flujo de calor, temperaturas graficadas en un tercer eje, etc. (opciones presentes bajo la pestaña Plot, optando por Plot Parameters).

Finalmente, los resultados expresados como matrices correspondientes a las temperaturas puntuales, las coordenadas de cada punto, la identificación numeral de las mismas y los triángulos definidos por familias de 3 puntos pueden ser todos exportados a la página principal de Matlab para ser allí procesadas (las pestañas de Mesh y Solve tienen la opciones de  Export Mesh y Export Solution).

 

 

Limitaciones del método numérico

Al concluir nuestros cálculos, terminamos con valores de temperatura en función de la posición (coordenadas x, y) y tiempo (en el caso del estado no estacionario). En muy pocos casos sin embargo son las temperaturas T = f(x, y, t) la solución buscada a un problema real. Las verdaderas respuestas buscadas a problemas reales están más asociadas a los flujos de calor, a predecir el destino final y el camino tomado por un sistema en base a sus condiciones iniciales, en resumen, a poder analizar y comprender una situación dada. Otro peligro que asecha al usuario es la naturaleza de “caja negra” que tiene la solución. No habiendo realizado personalmente los cálculos, no tenemos cómo verificar su pertinencia. Para contrarrestar estos aspectos, hemos diseñado una serie de prácticas que han sido aplicadas a lo largo de los últimos 5 años [1] y que buscan inducir un entendimiento cabal de los fenómenos de transferencia de calor, guardando siempre una actitud crítica hacia el programa que ejecuta los cálculos. Describimos a continuación algunas de las prácticas más significativas porque consideramos que ya ha llegado el momento de integrar las ecuaciones diferenciales parciales en la curricula de los estudiantes de ingeniería y esperamos que los ejemplos descritos contribuyan a establecer los paradigmas de su aplicación.. Todos los casos fueron resueltos con pdetool de Matlab y los resultados exportados a Matlab para ser procesados. En varios casos nos encontramos al límite de las capacidades del programa.

 

 

Análisis de isotermas

Anteriormente al uso de métodos numéricos, los ingenieros desarrollaron métodos gráficos para resolver problemas de transferencia de calor en 2 dimensiones. Aunque el método utilizado era muy limitado, no pudiendo incorporar condiciones de convección o radiación en las fronteras ni generación de calor al interior del objeto, resta que el análisis que se realizaba sobre las isotermas y las líneas de flujo retiene hoy en día todo su valor para poder visualizar los flujos de calor y comprender la naturaleza y particularidades del problema que estamos analizando.

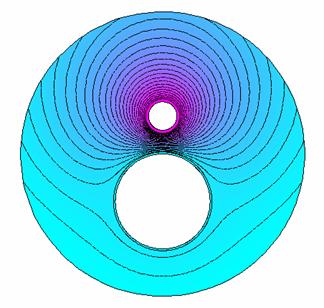
Figura 1:   Flujo de chocolate derretido en un tubo con aislante y un tutor con vapor para evitar su solidificación. Un análisis de las isotermas nos permite calcular el porcentaje de calor que el vapor pierde directamente hacia el exterior (aproximadamente 40%), el porcentaje de calor que le transfiere al chocolate (60%) y la proporción existente entre calor que le llega al chocolate y el calor que éste pierde hacia el exterior (relación de 5 a 3 aproximadamente). También es posible calcular la relación existente entre la conductividad en el tubo respecto a la conductividad del aislante.

 

Factores de forma y convección

Para situaciones de flujo de calor en 2 dimensiones, se recurrió en el pasado a la estimación de factores de forma S. Estos últimos eran calculados en base a métodos gráficos y permitían tratar un problema dado como si éste fuese simplemente un caso de flujo de calor unidimensional, con el factor de forma realizando las correcciones necesarias para compensar el efecto en 2 dimensiones. Existe una abundante literatura un tanto antigua en la cual se tiene expresiones para factores de forma aplicables a una gran cantidad de situaciones. Todos los valores de S citados adolecen sin  embargo de un defecto común, a saber que en todos los casos se supone que las  fronteras de los objetos están todos a la misma temperatura, situación difícilmente conciliable con la realidad en la cual condiciones variantes de convección crean temperaturas diferentes sobre la superficie de los objetos a través de la cual se transfiere calor.

Se ha retomado un ejemplo bastante común en los textos de transferencia de calor, a saber el de un ducto circular rodeado por un aislante de sección cuadrada. Dichos textos indican que el factor de forma para dicha situación puede calcularse por medio de la relación:

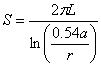                                                                                   [7]

donde a es el lado del aislante y r es el radio del tubo.

Dicho ejemplo ha sido retomado y resuelto bajo una serie de condiciones convectivas externas para poder determinar el factor de forma en  función de la constante convectiva externa. Como el problema tiene 4 planos de simetría, es posible circunscribir el planteamiento a una octava parte del mismo (ver figura 2, superior). Se encontró para el ejemplo en cuestión una relación lineal entre el factor de forma y la constante convectiva, tal que S = 0.4611*h + 51.2594. Si bien ambos métodos dan resultados bastante similares cuando la constante convectiva es pequeña, al alcanzar los valores más altos de h notamos que el error crece rápidamente, alcanzando una diferencia de 30% cuando h = 60.

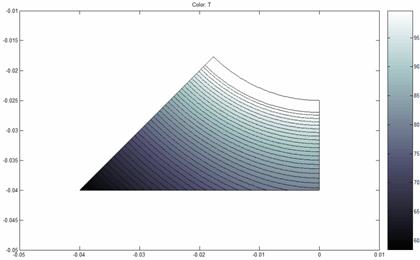
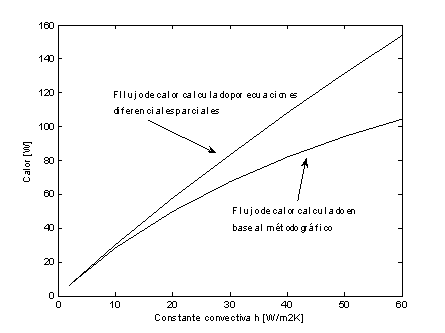
Figura 2:   (arriba) Base de cálculo para el problema de conducción en una tubería de sección circular rodeada por un aislante se sección cuadrada. Nótese que para la pared inferior difícilmente podría argumentarse de que está a una temperatura constante. (abajo) Flujos de calor calculados por el método de las ecuaciones diferenciales parciales y su comparación con valores calculados con ayuda de los factores de forma

 

Conducción de calor en 3 dimensiones con generación interna.

Un análisis de la reciente catástrofe acaecida en Fukushima-Daiichi  nos llevó naturalmente a interrogarnos sobre la temperatura a la que pueden llegar los pellets de material fisible cuando falla el sistema de enfriamiento. El desafío matemático de este proyecto consistía en calcular las temperaturas internas en un objeto en 3 dimensiones (pellets radioactivos), cuando el programa solo está diseñado para realizar cálculos en  objetos de 2 dimensiones. La simetría del pellet obviamente permite reducir sus dimensiones a 2, expresadas como el eje radial y el eje axial. Los estudiantes tuvieron que modificar el ingreso de las variables para tomar en cuenta aspectos como por ejemplo que las distancias crecían linealmente según los ejes, pero que las áreas de transferencia variaban según el eje siendo éste constante según el eje radial pero proporcional al eje axial. De similar manera, la cantidad de calor generado variaba linealmente según el eje axial pero al cuadrado del eje radial. Para validar sus modificaciones se realizaron varios modelos exploratorios como por ejemplo  el cálculo simple de conducción a través de un tubo, representando este último como una pared en el cual el eje x corresponde al eje radial y comparando los resultados obtenidos con la solución analítica del mismo.

El modelo desarrollado permitió explorar una diversidad de situaciones como son por ejemplo:

• los efectos de la variación de la constante convectiva sobre la temperatura máxima y promedia en el pellet;
• para un volumen de pellet constante, qué relación de largo a diámetro lleva a la máxima temperatura interna;
• cómo varían las temperaturas máximas y promedias cuando el pellet cambia de forma (cilindro hueco, esfera, etc.), etc.

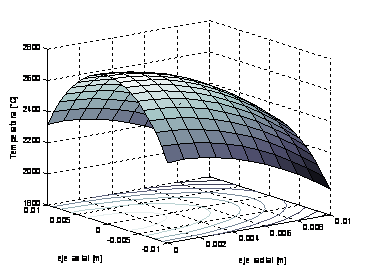
Figura 3:    Temperaturas en un pellet de material fisible de 2 cm de largo (eje axial) y 2 cm de diámetro (eje radial). Se adoptaron valores típicos de generación de calor en pellets de combustible nuclear. La figura ilustra la situación cuando la constante convectiva cae a 200 W/m²K

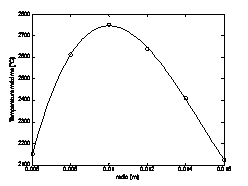
Figura 4:    Algunos valores calculados para los pellets radioactivos. Efecto de la constante convectiva sobre la temperatura máxima (izquierda). Temperatura máxima al interior de un pellet de volumen constante en función al radio del mismo (derecha).

 

Estado no estacionario y número de Biot

Al abordar el tema de flujo de calor en estado no estacionario, la primera solución con la que nos topamos es la solución de Newton, caracterizada por el hecho de que la relación de conductividad respecto a convectividad es muy grande. En la práctica, dicha condición está cuantificada por un número de Biot más pequeño que 0.1:

                                                                                  [8]

donde x₁ = volumen/área

El valor de 0.1 aparece mágicamente y muy pocos textos discuten el criterio detrás de dicha cifra, su origen histórico, el rango de error que representa y las limitaciones existentes en cuanto a su aplicación a objetos con pequeños factores de esfericidad. El análisis del estado estacionario por medio de aplicación de ecuaciones diferenciales parciales a una gran variedad de formas diferentes permitió apreciar mejor los límites y alcances del criterio de N_Bi < 0.1.

 

Flujo de calor en 2 dimensiones y estado no estacionario.

Cuando los textos de transferencia de calor [4] abordan el estado no estacionario encontramos una abundancia de gráficos en los cuales se puede inferir una temperatura reducida ya sea puntual ya sea promedio en función a la relación existente entre dimensión reducida, conducción y convección (h*x/k) y el tiempo reducido (a*t/x²).

Generalmente dichos gráficos se limitan a objetos sencillos como son una pared, un cilindro y una esfera, y típicamente adolecen de limitaciones en cuanto a los valores de conducción, convección y posición que podemos seleccionar, resultando en que las aplicaciones prácticas que se les puede dar son un tanto limitadas.

Hemos elaborado gráficos similares a los anteriormente descritos para objetos complejos. En el caso ilustrado a continuación, hemos tomado el nombre de nuestra publicación: Acta Nova, para crear un objeto cuyas paredes norte y este están aisladas y cuya temperatura cae desde 100ºC a 0ºC. Los resultados obtenidos en pdetool (figura 5) fueron exportados a Matlab y procesados para calcular la temperatura promedio en función al tiempo y la constante convectiva. Finalmente se elaboraron los diagramas típicos para el sistema (figura 6). Los datos obtenidos también fueron utilizados para explorar otros temas de interés como ser el estudio de la evolución de los puntos de mayor tensión mecánica (por efecto de mayor gradiente de temperaturas) en función al tiempo y la posición. Nótese que dicho análisis es prácticamente imposible si nos limitamos a las gráficas típicas de temperatura reducida en función al tiempo reducido.

t = 0,01

t = 1

t = 10

t = 50

t = 100

t = 200

t = 300

t = 600

t = 1000

Figura 5:    Evolución de temperaturas en función a su posición y el tiempo para un cuerpo complejo.

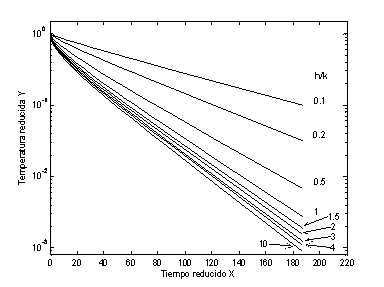
Figura 6:    Evolución de la temperatura promedio reducida en función al tiempo reducido para diferentes proporciones entre convección y conducción.

 

Max Planck y el congelado de papas prefritas

Los problemas de transición de fase son notoriamente difíciles de modelar y pdetool no tiene ninguna opción para incorporar fenómenos de generación de calor en cantidades limitadas (o en proporción a su masa) y en función de la temperatura, de modo que reacciones químicas en fase sólida están también excluidas por el momento.

Existe sin embargo un modelo sencillo para congelado propuesto por el gran físico alemán Max Planck. El planteamiento de Planck se resume a considerar la transición de fase como el factor limitante en la transferencia de calor de manera que el frente congelado penetra al interior del objeto en congelamiento con una velocidad limitada por la capacidad de conducir calor a través del hielo. Dicho de manera más matemática tenemos que:

                                                                         [9]

Hemos adaptado el planteamiento de Planck a un problema de congelamiento en 2 dimensiones e incluido fenómenos de convección para diseñar un proceso de congelado en continuo de papas prefritas. Los resultados obtenidos por cálculo fueron luego cotejados con datos experimentales obtenidos al medir la temperatura interna de una papa prefrita expuesta a aire frío a diferentes temperaturas y velocidades de aire. Se encontró una buena correlación entre los datos experimentales y los calculados. Los detalles del modelo y de las mediciones realizadas serán publicados próximamente [2].

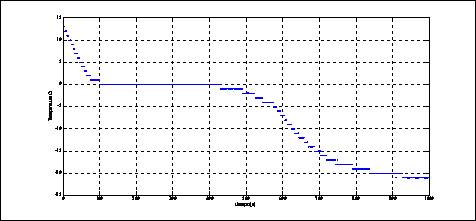
Figura 7:    Datos experimentales de la temperatura en el centro de una papa prefrita en función al tiempo [2]. El aire externo estaba a -20°C y la ráfaga de aire sobre la papa era de 8.4 m/s. El tiempo de congelado (transición de fase) se inicia aproximadamente a los100 segundos y concluye a los 400 segundos, intervalo de tiempo predicho por nuestro modelo con buena precisión.

 

A manera de conclusión

Se han expuesto algunos de los proyectos y prácticas abordados en los últimos 5 años que requerían el uso de ecuaciones diferenciales parciales. Los proyectos y prácticas fueron diseñados de manera a intentar romper con los moldes un tanto convencionales que limitan un aprendizaje significativo de la transferencia de calor. Se buscó que los temas abordados no tuvieran una solución fácil y de hecho nunca se anunció que las ecuaciones diferenciales parciales eran el método a emplearse para un problema dado, muchas de las prácticas desarrolladas aunque no descritas aquí requerían otro tipo de tratamiento. También se buscó realizar cruces entre los diferentes temas abordados en clases de manera que los estudiantes tuviesen que descubrir las relaciones existentes entre diferentes fenómenos en acción al interior de un problema dado. Los estudiantes salieron especialmente beneficiados en la medida que pudieron explorar y jugar con ecuaciones diferenciales parciales, aplicándolas a la resolución de problemas reales y a tener que razonar críticamente en la aplicación de un programa que realiza cálculos complejos.

 

 

---

Bibliografía

[1]      Amurrio, D. Proyectos de semestre para Procesos Unitarios II.         [ Links ]

[2]      Barrientos, P.; Amurrio, D. 2012. Artículo en elaboración        [ Links ]

[3]      Fourier, J. Memoire sur la propagation de la chaleur dans les corps solides  http://gallica.bnf.fr/ark:/12148/bpt6k33707/f220 último acceso  08.2011        [ Links ]

[4]      Geankoplis, C. Transfer Operations and Unit Processes. Prentice Hall         [ Links ]

[5]      Kreyszig  Advanced Engineering Mathematics. Wiley        [ Links ]

[6]      Mathworks 2005. Partial Differential Equation Toolbox For use with Matlab. Comsol AB. Mathworks Inc.

---

[1] Mémoire sur la propagation de la chaleur dans les corps solides. Presentado el 21 de diciembre de 1807 en el Institut National y transcrito por Poisson en el Nouveau Bulletin des Sciences para la Société Philomatique de Paris. t.I, p.112-116 N° 6; mars 1808. Paris, Bernard.