Programando con restricciones

 

 

Rodrigo Ronald Gumucio Escobar

RGumucio@gmail.com

 

 

---

Resumen: Muchas veces nos encontramos con problemas de combinatoria difíciles de resolver. Estos problemas aparecen comúnmente no solo en el ámbito académico (por ejemplo en los dominios de la inteligencia artificial, bases de datos, investigación operativa, etc.), sino también en el ámbito de nuestra vida cotidiana (por ejemplo en las áreas de planificación, programación de actividades, asignación de recursos, etc.).

Programando con restricciones es posible en muchos casos encontrar, de manera altamente eficiente, soluciones a muchos de estos problemas manejando su complejidad de manera simple e, incluso, elegante.

Este artículo es una introducción a la programación con restricciones. Describe de manera sencilla una buena parte de las técnicas y conceptos fundamentales que la sustentan a través de ejemplos abordados de manera clara y concisa. Finaliza con un ejemplo práctico y concreto, mostrando la resolución de un problema clásico usando C++.

Palabras clave: programación declarativa, problema de combinatoria, restricción, programación con restricciones

Abstract: Hard combinatorial problems are ubiquitous in our society. They arise in many application domains (e.g., artificial intelligence, data bases, operations research, etc.) and diverse real life settings (e.g., scheduling, timetabling, resource allocation, etc.).

Constraint Programming is a technique that manages the complexity of these problems in a simple and even elegant manner. It usually allows us to highly efficiently find solutions to many hard combinatorial problems.

This article is an introduction to Constraint Programming. It describes many of its fundamental concepts and techniques through clear and concise examples. It finishes with a practical example, solving a classical problem, using C++.

Key words: declarative programming, combinatorial problem, constraint, constraint programming

---

 

 

1   Introducción

Resolver un problema programando con restricciones se reduce a modelar dicho problema en términos de restricciones.[1] Como es habitual en la programación declarativa, no es necesario describir paso a paso el conjunto de instrucciones que producirán una solución, basta con describir el problema (es decir, detallar las características de su solución sin conocerla).

Las tecnologías basadas en restricciones, entre ellas la programación con restricciones y la búsqueda local basada en restricciones, se ocupan principalmente de proveer los mecanismos internos que permitirán a los lenguajes de programación declarativa encontrar eficientemente soluciones a los problemas expresados en términos de restricciones.

Los problemas que pueden ser expresados en términos de restricciones, particularmente problemas de combinatoria, son llamados problemas de restricciones y para ser resueltos requieren que todas sus restricciones sean cumplidas y, opcionalmente, que el costo (o beneficio) sea minimizado (o maximizado).

Informalmente, una restricción es una secuencia de variables junto con las combinaciones de valores permitidas para dicha secuencia. Las tecnologías basadas en restricciones calculan soluciones a problemas de restricciones razonando en torno a las restricciones que definen el problema, las variables sobre las cuales las restricciones han sido definidas, y los dominios finitos (es decir, los posibles valores) de estas variables.

La programación con restricciones es una técnica general para resolver problemas de restricciones. Como tal, dado cualquier problema modelado con restricciones, se ocupa primero de reducir el espacio de posibles soluciones y, luego, de ejecutar métodos específicos de búsqueda.

 

2   Modelado

Un buen ejemplo de problema de restricciones es el rompecabezas Sudoku:[2]

Colocar dígitos (excluyendo el cero) en una tabla de dimensiones , compuesta por  bloques adyacentes de dimensiones , de manera que (en la tabla) cada columna, fila, y bloque, contenga todos los dígitos del uno al nueve sin repetición.

Dado que solo es posible escoger dígitos del  al , este problema puede ser modelado estableciendo 27 restricciones: para cada fila, columna, y bloque, se establece que todos sus dígitos deben ser diferentes. Si las 27 restricciones se cumplen, el problema está resuelto.

Definición 2.1. (Restricción [2]). Dada una secuencia finita de variables con dominios , de manera que cada variable toma valores en . Una restricción en es un subconjunto de.

La secuencia de variables sobre la cual está definida se denota , y se dice que una secuencia de valores  cumple la restricción si y solamente si .

Un ejemplo de restricción (útil para modelar el problema del rompecabezas Sudoku) es  [3], definida sobre una secuencia  de  variables de tipo entero, que se cumple si y solamente si cada par de variables enteras  y toma valores diferentes para  (con ).

De hecho, esta restricción es un ejemplo de restricción global ya que puede ser definida en un número variable  (no fijo) de variables. La programación con restricciones le debe gran parte de su éxito al descubrimiento de las restricciones globales y por tanto es muy importante entenderlas.

Definición 2.2. (Restricción global). Una restricción global, denotada , es una restricción cuyo número de variables (sobre la cual está definida) es especificado por el parámetro (con ).

Modelando un problema, típicamente, uno encuentra que las restricciones globales pueden ser expresadas de manera alternativa como la conjunción de varias restricciones no globales (definidas en un número fijo de variables). Sin embargo, las restricciones globales juegan un papel importante en la búsqueda de soluciones porque traducen de mejor manera la estructura del problema y logran que el proceso de resolución sea mucho más eficiente. En consecuencia, el modelado usando restricciones globales es altamente recomendado.

Por ejemplo, es posible exigir que tres variables tomen valores distintos usando una única restricción , pero también, de manera alternativa, usando tres restricciones no globales . Una restricción (no global) , definida en dos variables, se cumple si y solamente si el par de variables enteras e toman valores distintos.

La programación con restricciones, como veremos más adelante, intenta encontrar soluciones a problemas de restricciones reduciendo el tamaño de los dominios de las variables (razonando sobre estos usando las restricciones establecidas) hasta que todas las restricciones sean cumplidas o hasta determinar que no existe ninguna solución.

Sean tres variables , , y , con dominios , , y , respectivamente. Usando las tres restricciones , , y , no es posible inferir nada acerca de la solución (por lo que es necesario recurrir a una búsqueda). Al contrario, dadas las mismas tres variables, con los mismos dominios, y una sola restricción , es posible inferir que una solución existe y además que .

Definición 2.3. (Problema de restricciones). Un problema de restricciones es una tripleta con

·         un conjunto finito de variables,

·         un conjunto finito de valores posibles para las variables en , es decir, su dominio, y

·         un conjunto finito de restricciones.

Cada una de las restricciones  en  es definida de manera tal que , y todas las variables en comparten (inicialmente) el mismo dominio [1].[3]

 

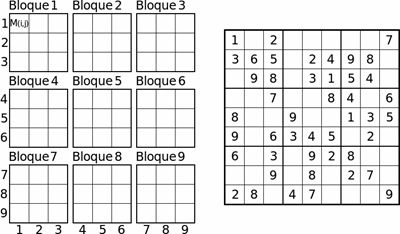
Figura 1:   Modelo para el problema Sudoku (izquierda). Asignación inicial de algunas variables para dar lugar a una instancia sencilla de este problema (derecha).

El problema Sudoku (ver Figura 1), descrito al inicio de esta sección, puede entonces ser expresado usando una matriz de  variables enteras en  con dominios , y  restricciones en . De manera que el problema de restricciones para Sudoku está dado entonces por la tripleta  con:

·        

·        

·        

¿Podrías definir el problema de las 8-reinas como problema de restricciones?

Colocar, en un tablero de dimensiones  , ocho reinas de manera que ninguna de ellas ataque a otra bajo las reglas del ajedrez.

Si bien es posible modelar este problema usando también solamente restricciones , existen, por supuesto, muchas otras restricciones (muy útiles e interesantes) ya diseñadas e implementadas que permiten modelar un gran número de problemas.[4]

 

 

3   Reducción por propagación

La programación con restricciones permite encontrar soluciones a problemas de restricciones realizando una búsqueda inteligente que de ser necesario (por ejemplo en problemas de optimización) llega a explorar (implícitamente) el espacio de posibles soluciones en su totalidad.

La forma ingenua de llevar a cabo una búsqueda completa, generando todas las posibles soluciones del problema en cuestión, no es práctico ni factible porque el espacio de posibles soluciones puede ser tan grande como podamos imaginar. La belleza de la programación con restricciones reside en su habilidad de, en la mayoría de los casos, evitar generar todas las posibles soluciones por medio de la reducción por propagación [1].

Los algoritmos que se ocupan de reducir el espacio de posibles soluciones son usualmente llamados algoritmos de reducción por propagación [2], y el denominador común de estos es el aprovechamiento de condiciones de necesidad para reconocer valores en los dominios de las variables que, si fueran asignados, violarían alguna restricción [1]. El único propósito de un algoritmo de reducción por propagación es entonces simplificar el problema que está siendo resuelto reduciéndolo a otro equivalente pero más pequeño.

Figura 2:   Resolución de una instancia del problema Sudoku usando solamente reducción por propagación.

Un concepto muy importante en los algoritmos de reducción por propagación es el de consistencia. Estos algoritmos reducen el tamaño de los dominios de las variables de acuerdo a un nivel de consistencia. Por ejemplo, tomemos nuevamente el problema clásico analizado como ejemplo en la sección anterior: sean tres variables , , y , con dominios , , y  respectivamente.

Si  o , entonces sería imposible asignar valores diferentes a e, y por tanto no existiría ninguna solución. Esto significa que el dominio de  puede ser reducido a . Sin embargo, considerando las tres restricciones , , , y , no fue posible hacer esta inferencia. Al contrario, usando una única restricción global , sí fue posible hacer esta inferencia. Por tanto, decimos que el nivel de consistencia de  puede ser más alto que el nivel de consistencia usando 3 restricciones .

En el nivel más alto de consistencia, se garantiza que todos los valores que no participan de ninguna solución sean eliminados del dominio de las variables correspondientes. Con los niveles de consistencia más bajos simplemente se realiza alguna reducción en los dominios cuando una variable es asignada (es decir cuando la cardinalidad de alguna variable es reducida a 1).

Por ejemplo, usando un nivel de consistencia denominado comprobación de coherencia, para una restricción , toda vez que un valor  es asignado a una variable , todos los valores en los dominios de las otras variables en  que entran en conflicto con la restricción  (debido a que ) son eliminados. Por ejemplo, si  es  con ,  y ; si se asigna el valor  a la variable , entonces el algoritmo de reducción por propagación con un nivel de consistencia de comprobación de coherencia devuelve ,  y .

En la programación con restricciones, las restricciones se implementan a través de propagadores. Un propagador es una función  que lleva a cabo reducción por propagación [5]. Por tanto, los propagadores son funciones que se aplican a un conjunto de los dominios de las variables en , denotado , y básicamente lo que hacen es reducir los dominios de estas variables eliminando los valores que no pueden ser asignados de acuerdo con la restricción que implementan.

Los propagadores deben cumplir, fundamentalmente, tres propiedades:

1.       Nunca añaden valores a los dominios de las variables. Es decir, solo les está permitido eliminar ningún, uno, o varios valores.

2.       Nunca eliminan soluciones de la restricción que implementan. Es decir, solo les está permitido eliminar valores de los dominios de las variables siempre y cuando ninguna solución sea eliminada en el acto.

3.       La función  que lleva a cabo reducción por propagación es monotónica.

Si en algún momento alguno de los dominios contenidos en  es vacío, decimos que  ha fallado, y que por tanto no fue posible encontrar una solución. Cuando ya no es posible realizar más reducción por propagación y todos los dominios contenidos en  tienen cardinalidad uno, hemos encontrado una solución.

Dado un problema de restricciones , donde el conjunto de propagadores que implementan las restricciones en  es , y el conjunto de dominios iniciales de las variables es , el algoritmo básico de reducción por propagación es el mostrado en la Figura 3.

1 mientras existacon

2     

3 retornar

Figura 3:   Algoritmo básico de reducción por propagación.

Las tres propiedades fundamentales de este algoritmo son:

1.       El algoritmo siempre termina.

2.       El algoritmo no elimina ninguna solución.

3.       Si , entonces  es el punto fijo simultáneo más grande (o más débil) de todos los propagadores en .

Una demostración de que estas propiedades se cumplen puede ser encontrada en [5]: el algoritmo termina porque los propagadores nunca añaden valores a los dominios de las variables, y las otras dos propiedades son consecuencias directas de las propiedades individuales de los propagadores.

Evidentemente, el algoritmo mostrado en la Figura 3 es muy simple y puede ser considerablemente optimizado (ver [5]). Una consecuencia importante de estas propiedades es que los propagadores pueden ser invocados en cualquier orden, es decir, el orden en el cual los propagadores son aplicados no afecta el resultado de la reducción por propagación.

En la Figura 2 se ilustra el proceso de resolver (mecánicamente) la instancia del problema Sudoku presentado en la Figura 1, donde algunas variables ya estaban asignadas en . Como el ejemplo muestra, algunas veces es posible encontrar soluciones usando solamente reducción por propagación. Sin embargo, en la mayoría de los casos la reducción por propagación no es suficiente por sí sola y por tanto es necesario recurrir a algoritmos de búsqueda.

¿Podrías encontrar una solución al problema de las 8-reinas usando solamente la reducción por propagación?

 

 

4   Búsqueda sistemática

En la programación con restricciones, toda vez que la reducción por propagación no es suficiente por sí sola, para encontrar una solución, se recurre a algoritmos de búsqueda sistemática. Estos algoritmos, sin embargo, no están de ninguna manera libres de la reducción por propagación ya que esta se ejecuta después de cada paso durante la búsqueda.

Una vez que se determina que la reducción por propagación no puede encontrar una solución por sí misma, se empieza a buscar la solución dividiendo (o partiendo) el problema en otros subproblemas más pequeños o simples. La reducción por propagación es ejecutada, luego, en cada uno de estos subproblemas. El patrón general de búsqueda consiste, por tanto, en el uso alternado de la subdivisión del problema y la reducción por propagación [2].

Típicamente un algoritmo de búsqueda requiere tanto de un árbol (de búsqueda) como de un algoritmo de exploración. En la programación con restricciones, los llamados ramificadores están a cargo de definir el árbol de búsqueda mientras que los algoritmos de exploración construyen, incrementalmente, el árbol hasta que una solución (o todas las soluciones, o la solución óptima) sea encontrada. Los algoritmos de exploración no siempre toman decisiones correctas (que llevan inmediatamente a encontrar soluciones), algunas veces cometen errores de los cuales necesitan aprender para luego retroceder y tomar otra (mejor) decisión.

El propósito de los ramificadores es tomar decisiones informadas, de acuerdo a alguna heurística, para sugerir nuevas restricciones que permitan dividir el problema en subproblemas de manera inteligente. Usualmente, una heurística requiere que el ramificador tenga acceso, por lo menos, al conjunto de dominios de las variables (por ejemplo, para determinar cuál es la variable con el dominio más pequeño) y el conjunto de propagadores (por ejemplo, para determinar cuál es la variable sobre la cual está defina la mayor cantidad de restricciones).

Por ejemplo, un ramificador, con una heurística simple, seleccionaría de un problema de restricciones una variable  junto con un valor  de su dominio (de cardinalidad mayor a uno) y sugeriría la restricción  para dividir el problema en dos subproblemas: uno obtenido añadiendo la restricción  , y otro obtenido añadiendo la restricción  . Esta sencilla estrategia usualmente se optimiza seleccionando la variable con el dominio más pequeño y toma el nombre de heurística de fallar pronto.

Un ramificador debe mostrar un buen comportamiento de manera que [5]:

·         el árbol de búsqueda se mantenga finito,

·         ninguna solución sea perdida durante la búsqueda, y

·         las soluciones no se repitan.

Definición 4.1. (Ramificador). Un ramificador es una función que toma como entrada un conjunto de propagadores  junto con el conjunto de los dominios de las variables en cuestión , y produce una tupla  de conjuntos de propagadores .

Asumamos que  para  y . Entonces, un ramificador  debe ser:

1.       completo, es decir, ,

2.       disjunto, es decir,  para  con , y

3.       decreciente, es decir, los elementos de  deben tener menor o igual cardinalidad a los elementos de .

El cumplimento de estas propiedades aseguran que un ramificador  tenga un buen comportamiento. La completitud garantiza que ninguna solución es perdida; la disjunción garantiza que ninguna solución aparezca repetida en el árbol; y la propiedad de ser decreciente garantiza que las restricciones sugeridas provocarán reducción por propagación. De esta manera el árbol será finito [5].

Definición 4.2. (Árbol de búsqueda). Un árbol de búsqueda para un problema de restricciones y un ramificador , es un árbol cuyos nodos son nombrados con pares  donde  es un conjunto de propagadores, y el resultado de ejecutar la reducción por propagación con respecto a . De ahí que:

·         la raíz del árbol es nombrada , donde  es obtenido de

·         para cualquier hoja,

o        podemos decir que ha fallado, y por tanto que el nodo hoja ha fallado; o bien

o        podemos decir que el nodo hoja ha sido resuelto cuando ;

·         finalmente para cualquier nodo interno ,  no ha fallado y con . Por tanto, un nodo interno tiene  nodos hijos, donde el -ésimo nodo es nombrado, con , .

Por construcción, para un nodo  en el árbol de búsqueda,  es un punto fijo simultáneo de . También debido a la propiedad decreciente de los ramificadores, dados dos nodos  y , si el primero está en la misma rama que el segundo, pero más abajo, entonces los elementos de  deben tener menor o igual cardinalidad a los elementos de  [5].

Una solución al problema de restricciones estará dada por un nodo hoja donde todos los dominios de todas las variables tengan cardinalidad uno, es decir, donde todas las variables hayan sido asignadas de manera que todas las restricciones se cumplan.

Dado un ramificador, la exploración de un árbol es el proceso de construir el árbol hasta que la primera solución sea encontrada, un cierto número de soluciones sean encontradas, todas las soluciones sean encontradas, o incluso hasta que ninguna o la más óptima solución (con respecto a una medida de calidad) sea encontrada.

Dos típicas estrategias de exploración son la búsqueda en profundidad y la búsqueda por ramificación y acotación. La Figura 4 muestra el algoritmo para la búsqueda en profundidad [5] donde, por simplicidad, restringimos nuestra atención a los ramificadores que retornan o una tupla vacía  o un par  (en lugar de una tupla de  elementos).

Figura 5:   Ejemplo de búsqueda en profundidad.

Por ejemplo, consideremos un problema de restricciones con , , y . La Figura 5 muestra el árbol de búsqueda para este problema con la heurística simple descrita al inicio de esta sección. En el árbol, un círculo representa un nodo con un dominio de cardinalidad mayor a uno, un cuadrado representa un nodo que ha fallado y un diamante representa un nodo resuelto.

¿Podrías resolver el problema de las 8-reinas usando (además de reducción por propagación) un ramificador con heurística de fallar pronto y el algoritmo presentado en la Figura 4?

En los problemas de optimización, cuando se intenta buscar la mejor solución con respecto a una medida de calidad, calcular todas las soluciones y luego seleccionar la que minimice el costo (o maximice el beneficio) es impráctico puesto que en problemas difíciles de combinatoria, el número de soluciones crece exponencialmente con el tamaño del problema.

La búsqueda por ramificación y acotación se usa para resolver tales problemas de optimización. Esta búsqueda se realiza como una versión modificada de la búsqueda en profundidad mostrada en la Figura 4. La idea es emplear la información ya obtenida para reducir considerablemente el espacio de búsqueda de soluciones.

La información ya obtenida, con respecto a la solución, es expresada en términos de restricciones: toda vez que se encuentra una solución, una restricción adicional es añadida al modelo exigiendo que cualquier otra solución encontrada debe ser mejor a las ya encontradas anteriormente. Con esta restricción adicional, el árbol de búsqueda se vuelve considerablemente más pequeño.

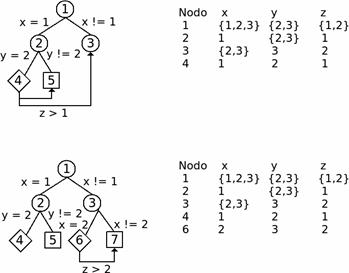
Figura 6:   Ejemplo de búsqueda por ramificación y acotación.

Consideremos, por ejemplo, un problema de restricciones con , , y . El objetivo es encontrar una solución con el valor más grande posible para . Nuevamente, usando la heurística simple descrita al inicio de esta sección, la Figura 6 muestra el árbol de búsqueda para la solución óptima a este problema.

Para empezar, la primera solución es encontrada usando la búsqueda en profundidad. El valor para  en esta solución es , por tanto una nueva restricción  es añadida. Luego, el nodo 5 falla porque  reduce a , y el nodo 3 reduce a  . Luego, el nodo 3 se divide en dos nuevos: los nodos 6 y 7. El nodo 6 es una nueva y mejor solución con , por tanto la restricción  es agregada al nodo 7 lo cual hace que falle. Finalmente, la mejor solución es , , y  . Estos dos últimos ejemplos con sus respectivas figuras fueron tomados de [4].

¿Podrías, tomando inspiración del algoritmo presentado en la Figura 4, escribir el algoritmo correspondiente a la búsqueda por ramificación y acotación?

De esta manera, la programación con restricciones resuelve problemas explorando (implícitamente) todo el espacio de posibles soluciones, realizando una búsqueda de manera sistemática (aprendiendo y retrocediendo cuando es necesario), dando lugar a un árbol de búsqueda donde la reducción por propagación es ejecutada en cada nodo.

 

 

5   Un ejemplo práctico

En esta sección se resuelve, programando con restricciones, el problema de las n-reinas. La solución es implementada en el lenguaje C++ usando la librería Gecode[5] (tanto el código fuente como las explicaciones están basadas en las presentadas dentro la documentación de su distribución).

Generalizando la formulación del problema de las 8-reinas presentado en la sección 2, el problema de las n-reinas exige:

Colocar, en un tablero de dimensiones , con ,  reinas de manera que ninguna de ellas ataque a otra bajo las reglas del ajedrez.

Las restricciones para modelar este problema son:

·         ningún par de reinas debe ser colocada en la misma columna,

·         ningún par de reinas debe ser colocada en la misma fila,

·         ningún par de reinas debe ser colocada en la misma diagonal de arriba a abajo de izquierda a derecha, y

·         ningún par de reinas debe ser colocada en la misma diagonal de arriba a abajo de derecha a izquierda.

Una posible representación de este problema de restricciones usa  variables de tipo entero, , cada una con dominio [2], de manera que cada variable  denota la posición, es decir la fila, de la reina colocada en la -ésima columna del tablero.

Las restricciones pueden entonces ser expresadas como:

·         ,

·         ,[6] y

·          .

En esta representación, la restricción de que ningún par de reinas debe ser colocada en la misma columna es implícita (y por tanto está ausente de la anterior lista de restricciones). Puesto que tenemos  reinas y  filas, y ningún par de reinas pueden convivir en la misma columna, cada columna debe contener exactamente una reina. Consecuentemente, una variable fue creada para cada columna, y los valores tomados por estas variables representan la fila de la reina correspondiente. Por tanto, no es necesario exigir explícitamente que ningún par de reinas se ataquen verticalmente. Una restricción implícita, en este caso producida por la forma en que se modela el problema, nunca será violada y es rígida en ese sentido.

Con el objetivo de enfatizar que el uso de restricciones globales es altamente recomendado, es oportuno hacer notar que, en el modelo de este problema, se da preferencia al uso de restricciones  sobre el uso de conjunciones de  restricciones  (una restricción  para cada  y ).

Un modelo de un problema de restricciones, en Gecode, es implementado usando un espacio en el que se definen las variables (de decisión), los propagadores (implementaciones de restricciones) y los ramificadores (que definirán el árbol de búsqueda).

Programa 5.1 Estructura de un programa heredando la clase Space de Gecode.

1 using namespace Gecode; 
2
3 class Reinas : public Space {
4     /// Constructor: implementación del modelo
5     /// Constructor de copia: para clonar objetos
6     /// Función de copia: para copiar durante la   clonación de objetos
7     /// Función para imprimir la solución
8 };
9 /// Función principal

Prácticamente, toda la funcionalidad necesaria se encuentra visible dentro del espacio de nombres Gecode (Línea 1 del Programa 5.1). Los Espacios están implementados por la clase Space, de manera que para implementar el modelo es necesario heredar de esta clase e implementar el modelo en el constructor (de la subclase). Además del constructor, para que la búsqueda funcione apropiadamente es necesario implementar, en la subclase, un constructor de copia, y una función de copia.

Programa 5.2. Variables de decisión

1 #include <gecode/int.hh>
2
3 using namespace Gecode;
4
5 class Reinas : public Space {
6    protected:
7      IntVarArray reina;  
8    public:
9      Reinas() {
10        const int n = 8; 
11        reina = IntVarArray(*this, n, 0, n - 1);
12         /// Establecer restricciones
13         /// Especificar ramificador
14     }
15   /// Constructor de copia: para clonar objetos
16   /// Función de copia: para copiar durante la clonación de objetos
17   /// Función para imprimir la solución
18 };
19 /// Función principal

Para implementar el modelo, por simplicidad, definimos una constante de tipo entero  (que normalmente sería un parámetro obtenido desde la línea de comando) para especificar el número de reinas, y un vector  de  variables de decisión de tipo entero (Líneas 7 y 10 del Programa 5.2). Para usar variables de decisión y restricciones de tipo entero, es necesario incluir <gecode/int.hh>.

El constructor del vector de variables de decisión de tipo entero toma como primer argumento el espacio actual. (De hecho, cualquier función que dependa del espacio, toma al espacio actual como argumento y por tanto esto se repite en los constructores de variables de decisión, funciones que establecen restricciones, y funciones que especifican ramificadores.)

Programa5.3. Restricciones

1 #include <gecode/int.hh>
2
3 using namespace Gecode;
4
5 class Reinas : public Space {
6    protected:
7      IntVarArray reina;
8
9    public:
10     Reinas() {
11       const int n = 8;
12       reina = IntVarArray(*this, n, 0, n - 1);
13
14       distinct(*this, reina, ICL_VAL);  
15       IntArgs c(n); 
16       for (int i = n; i--; ) c[i] = i;
17       distinct(*this, c, reina, ICL_VAL);  
18       for (int i = n; i--; ) c[i] = -i;
19       distinct(*this, c, reina, ICL_VAL);  
20
21       /// Especificar ramificador
22     }
23   /// Constructor de copia: para clonar objetos
24   /// Función de copia: para copiar durante la clonación de objetos
25   /// Función para imprimir la solución
26 };
27 /// Función principal

Para lograr expresar las restricciones en las diagonales del tablero, en el constructor, declaramos un vector de argumentos de tipo entero IntArgs (Línea 15 del Programa 5.3). La memoria asignada a los vectores de variables de decisión (como IntVarArray) se libera solamente cuando termina la vida del espacio en el que han sido definidos. Esto hace que este tipo de vectores no sean adecuados para variables temporales, en este caso para ser usados como argumentos en la especificación de restricciones. Los vectores de tipo IntArgs, al contrario, son inmutables, obtienen espacio del heap, y la memoria es liberada cuando su destructor es ejecutado.

La implementación de la restricción  en Gecode es llamada restricción distinct. Establecer distinct(space, x) (Línea 14 del Programa 5.3) exige que todas las variables en  tomen valores diferentes. De igual manera, establecer distinct(space, c, x) (Líneas 17 y  19 del Programa5.3), para un vector de valores enteros  (de tipo IntArgs y del mismo tamaño que ), exige que  para  e  . Estas dos funciones pueden tomar un último parámetro especificando el nivel de consistencia para la reducción por propagación. En este caso, especificamos el nivel de consistencia por valores a través de la constante ICL_VAL indicando que la reducción por propagación se efectuará cuando alguna variable sea asignada.

Programa 5.4. Búsqueda

1 #include <gecode/int.hh>
2 
3 using namespace Gecode;
4 
5 class Reinas : public Space {
6  protected:
7    IntVarArray reina;
8 
9  public:
10    Reinas() {
11     const int n = 8;
12     reina = IntVarArray(*this, n, 0, n - 1);
13 
14     distinct(*this, reina, ICL_VAL);
15     IntArgs c(n);
16     for (int i = n; i--; ) c[i] = i;
17     distinct(*this, c, reina, ICL_VAL);
18     for (int i = n; i--; ) c[i] = -i;
19     distinct(*this, c, reina, ICL_VAL);
20 
21     branch(*this, reina, INT_VAR_SIZE_MIN, INT_VAL_MIN);  
22    }
23 
24    Reinas(bool share, Reinas& s) : Space(share,s){ 
25     reina.update(*this, share, s.reina);
26    }
27 
28    virtual Space* copy(bool share) {  
29     return new Reinas(share,*this);
30    }
31 
32  /// Función para imprimir la solución
33 };
34 /// Función principal

El siguiente paso es especificar un ramificador que, usualmente, toma un vector de variables que deben ser asignadas durante la búsqueda, junto con una estrategia de selección de variables y una estrategia de selección de valores.

En nuestro caso (Línea 21 del Programa5.4), usando una heurística de fallar pronto, especificamos para el vector de variables reinas, seleccionar primero las variables con el dominio de menor cardinalidad (a través de la constante INT_VAR_SIZE_MIN) y luego asignar primero el menor valor del dominio (a través de la constante INT_VAL_SIZE_MIN).

Por la manera en que la búsqueda es implementada en Gecode, es necesario implementar un constructor de copia (Línea 24 del Programa5.4) y una función de copia (Línea 28 del Programa 5.4). La función de copia es virtual para que sea posible crear una copia de un espacio aun cuando no se conozca la subclase exacta de este. El argumento share no debería preocupar al lector puesto que es usado internamente por Gecode.

Programa 5.5. Solución al problema de las n-reinas

1 #include <gecode/int.hh>
2 #include <gecode/search.hh>
3 
4 using namespace Gecode;
5 
6 class Reinas : public Space {
7  protected:
8    IntVarArray reina;
9 
10  public:
11    Reinas() {
12     const int n = 8;
13     reina = IntVarArray(*this, n, 0, n - 1);
14 
15     distinct(*this, reina, ICL_VAL);
16     IntArgs c(n);
17     for (int i = n; i--; ) c[i] = i;
18     distinct(*this, c, reina, ICL_VAL);
19     for (int i = n; i--; ) c[i] = -i;
20     distinct(*this, c, reina, ICL_VAL);
21 
22     branch(*this, reina, INT_VAR_SIZE_MIN, INT_VAL_MIN);
23    }
24 
25    Reinas(bool share, Reinas& s) : Space(share,s){
26     reina.update(*this, share, s.reina);
27    }
28 
29    virtual Space* copy(bool share) {
30     return new Reinas(share,*this);
31    }
32 
33    virtual void print(std::ostream& os) const {  
34     os<< "reinas\t" <<reina<<std::endl;
35    }
36 };
37 
38 int main(int argc, char* argv[]) {  
39  Reinas* m = new Reinas; 
40  DFS<Reinas> e(m); 
41  delete m;
42 
43  Reinas* s = e.next();  
44  s->print(std::cout); 
45  delete s;
46 
47  return 0;
48 }  

Finalmente, para encontrar la solución, además de una función para imprimir los valores asignados a nuestras variables de decisión (Línea 33 del Programa 5.5), es (por supuesto) necesario implementar la función principal que,

·         crea el modelo (Línea 39 del Programa 5.5),

·         crea un motor de búsqueda en profundidad (Línea 40 del Programa 5.5) incluido en <gecode/search.hh>,

·         busca la primera solución (Línea 43 del Programa 5.5), e

·         imprime la primera solución encontrada (Línea 44 del Programa 5.5).

El resultado es: reinas {0, 4, 7, 5, 2, 6, 1, 3}.[7] ¿Podrías comprobar que este resultado es correcto?

Una herramienta muy útil que ofrece Gecode es Gist: una interfaz gráfica y herramienta interactiva que permite explorar el árbol de búsqueda, inspeccionando sus nodos, ya sea paso por paso o automáticamente. El uso de Gist es afortunadamente simple. Para este caso, basta con incluir <gecode/gist.hh> y reescribir la función principal como se muestra en el Programa 5.6.

Programa 5.6. Función principal para usar Gist

1 int main(int argc, char* argv[]) {
2  Reinas* m = new Reinas;
3  Gist::Print<Reinas> p("Mostrar solucion");
4  Gist::Options o;
5  o.inspect.click(&p);
6  Gist::dfs(m,o);
7  delete m;
8 
9  return 0;
10 }

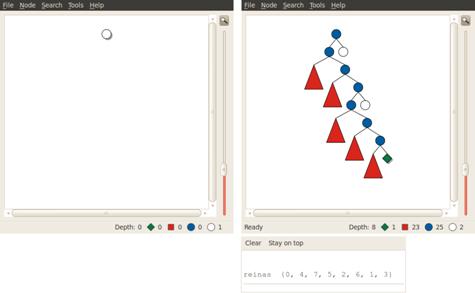
Figura 7:   Árbol de búsqueda mostrado por Gist para encontrar la primera solución al problema de las 8-reinas.

Ejecutando el nuevo programa,[8] podemos observar la raíz del árbol, y realizar la búsqueda paso por paso o automáticamente. Por ejemplo, si pedimos que la búsqueda se realice automáticamente hasta encontrar la siguiente (es decir, la primera) solución, obtenemos gráficamente el árbol construido hasta encontrar reinas {0, 4, 7, 5, 2, 6, 1, 3} tal como se muestra en la Figura 7.

¿Podrías escribir un programa en C++ usando Gecode (y Gist) para resolver instancias del rompecabezas Sudoku?

¡Se dice que las instancias más difíciles de Sudoku publicadas en los periódicos pueden ser resueltas fácilmente usando programación con restricciones en muy poco tiempo con pocos intentos fallidos en la búsqueda!

 

 

---

6   Referencias

[1]      Magnus Ågren. Set Constraints for Local Search. PhD thesis, Department of Information Technology, Uppsala University, Sweden, 2008. Disponible en http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-8373.         [ Links ]

[2]      Krzysztof R. Apt. Principles of Constraint Programming. Cambridge University Press, 2003.         [ Links ]

[3]      Jean-Charles Régin. A filtering algorithm for constraints of difference in CSPs. In Barbara Hayes-Roth and Richard E. Korf, editors, Proceedings of AAAI’94, pages 362–367. AAAI Press, 1994.         [ Links ]

[4]      Christian Schulte. Programming constraint services. Springer, 2002.         [ Links ]

[5]      Christian Schulte. Course Notes. Constraint Programming (ID2204). Spring semester. Royal Institute of Technology - KTH, 2011.         [ Links ]

[1] Y además, como veremos más adelante, a escoger un algoritmo de búsqueda.

[2] Problema ampliamente conocido gracias a numerosos periódicos que publican muchas de sus instancias en sus secciones de pasatiempos.

[3] No existe pérdida de generalidad exigiendo que todas las variables compartan inicialmente el mismo dominio, puesto que siempre es posible especificar dominios más pequeños para ciertas variables en a través de restricciones de pertenencia/membresía.

[4] Ver, por ejemplo, el catálogo de restricciones globales disponible en http://www.emn.fr/z-info/sdemasse/gccat/

[5] Código abierto y libre, bajo una licencia permisiva, disponible en http://www.gecode.org/

[6] denota una secuencia de variablestal que e

[7] Tras instalar correctamente Gecode, el programa mostrado en el Programa 5.5, guardado en un archivo reinas.cpp, puede ser compilado con el siguiente comando:
g++ reinas.cpp -o reinas -lgecodeint -lgecodesearch

[8] Compilado previamente con el comando :                           
g++ reinas-gist.cpp -o reinas-gist -lgecodeint -lgecodesearch -lgecodegist