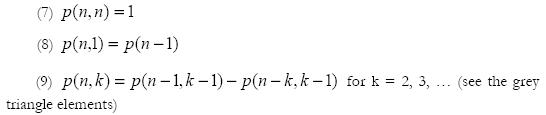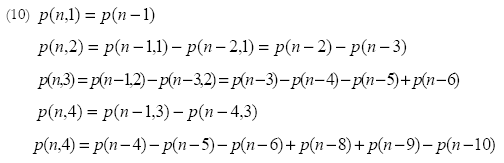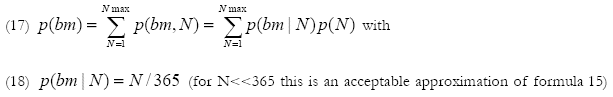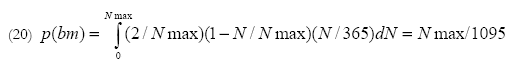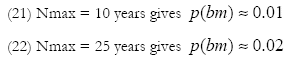Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Acta Nova
versión On-line ISSN 1683-0789
RevActaNova. vol.4 no.1 Cochabamba dic. 2008
Actualidad y divulgación
Euler's ship on the pentagonal sea
Johannes W. Meijer, Manuel Nepveu
TNO Built Environment and Geosciences, Princetonlaan 6, P.O. Box 80015, 3508 TA Utrecht, The Netherlands
e-mail: meijgia@hotmail.com and Manuel.Nepveu@tno.nl
Summary
Probability is a rich part of applied mathematics. First we have a look at the unique encounter of two 23 year old chess players on their birthday which leads to an interesting set of questions. Next some chess tournaments lead us to partition numbers, multinomial coefficients and Bell numbers. After that we arrive at the Pentagonal Sea where the beautiful structure of Euler's ship leads to a new look at the recurrence relation of the partition function and the pentagonal number theorem. Aboard Euler's ship we find the Lazy Caterer's and the Connell sequences. At the end we look at the probability that the above mentioned chess confrontation will ever happen again and tell you how to decide whether to accept or reject a wager.
1. Introduction
Hans Freudenthal pointed out in his book 'Mathematics as an Educational task' that probability is a paragon of applied mathematics [1]. Freudenthal gives examples like the discussion on betting strategies between Blaise Pascal and Chevalier de Méré and the genetic experiments of Gregor Mendel. He also mentions Joseph Bertrand's drawer problem, which is related to the Monty Hall problem. These problems have in common that they show our poor ability to assess chance intuitively. De Méré lost money rolling dice and Pascal showed him why. Few people believed Mendel's observation about his genetic experiments although what he said had a probability of almost one of being true. Applying a priori probability considerations to problems of physics may also turn out to be wrong, simply because our tacit assumptions are not honored by Nature. For instance, Feller wrote jokingly: "That our intuition fails so often isn't entirely out fault. Physical particles like photons and electrons, for example, are clearly not trained in our human common sense." [2]. So it is sensible to be careful.
Monty Hall was the most successful of all in creating confusion. Imagine that you have won a prize in Monty Hall's television show. He gives you the choice of three doors: Behind one door there is a car; behind the others, goats. You pick a door, say number 1, and Monty Hall, who knows what's behind the doors, opens another door, say number 3, and a goat appears. He then asks you: "Do you want to change your mind and pick door number 2?" What do you do? [3].
One of us (JWM) experienced first hand that probability can lead anyone into new territory. A simple random splitting experiment led to the discovery of the exponential integral distribution, which generalizes the gamma distribution [4].
In the following paragraphs we study the probability of events like coincident birthdays, coincident years of birth and the occurrence of such events during chess tournaments. Our considerations will lead to some surprising discoveries.
2. Coincident birthdays
On April 5, 2008, the International Grandmasters Erwin l'Ami and Jan Smeets played each other during the Dutch Chess Championship (DCC). The game wasn't remarkable; it was an uneventful draw. The fact that Smeets and l'Ami played each other on their birthday was already remarkable as we will soon see; but what made this game truly unique was that they played each other on their 23rd birthday since both players were born on April 5, 1985!
Let's have a look at the probability of this and some other events. We assume that the starting numbers for the twelve competing players are chosen at random and that all birthdays are equally likely. We also assume that all days of the year are equally likely to be the starting day for the DCC, and we'll skip February 29th just for ease.
Let's start with the question what the probability is that at least two of the twelve players have the same birthday. This probability is equal to 1 minus the probability that all players have a different birthday [5].
![]()
The probability of this event is 0.167, or 1 in 6, which is quite high. So it isn't surprising that two of the twelve players have the same birthday. The probability that these players have their birthday during one of the eleven rounds of the DCC is p = 0.167 x (11/365) = 0.005, or 1 in 200, while the probability that they play each other on their birthday is p = 0.167 x (1/365) = 0.00046, or 1 in 2186. So both events would be quite remarkable.
Now, what is the probability that two players, who were born on the same day of the same year, played each other on their birthday during the DCC of 2008? The oldest player that participated in the DCC of 2008 was 45 years old (born in 1963) and the youngest was 20 years old (born in 1987). Once again we assume that all years of birth between 1963 and 1987 are equally likely. In this case we have a time period of 25 x 365 = 9125 days. The probability that two of the twelve players were born on the same day can be calculated in a similar way as above.
![]()
The probability that these two players meet each other on their birthday is p = 0.0072 x (1/365) = 0.00002 or 1 in 50000. So it was indeed unique that Smeets and l'Ami played each other during the DCC of 2008 on their 23rd birthday since this event is extremely improbable [6].
3. Coincident years of birth
We have already said the oldest player was 25 years older than the youngest. Let's turn now to the question that two of the 12 players were born in the same year. Your intuition will probably tell you that this probability isn't too high so it may come as a surprise that it is almost 1.
![]()
A look at the years of birth of the 12 players revealed that there were four pairs of players who were born in the same year, i.e. 1985, 1987, 1979 and 1963. Is this remarkable?
Let's have a look at the probability that there are several pairs of players who are born in the same year. Let's assume a chess tournament with n players. The time period in which they were born is D years. The probability that there are x pairs, with x = 1, 2, 3, ... that are born in the same year (different years for each pair and the (n-2x) other players) is determined by
![]()
where the exclamation mark (!) is the sign for the factorial [7]. The interpretation of formula 4 is as follows. The number of x pairs from a population of n is given by [n(n-1)/2][(n-2)(n-3)/2].......[(n-2x+2)(n-2x+1)/2] which must be divided by (x!) because the order in which we take them together doesn't matter. This leads to the first factor [n!/{(n-2x)! (x!) (2)x}]. The probability that we have x pairs is [1/Dx] and the probability that there are (n-x) different years of birth, x for the pairs and (n-2x) for the rest of the players is [D!/{(D-n+x)! (Dn-x)}]. The product of these two formulas leads to the second factor.
With formula (4) we find for the DCC of 2008, that with n=12 players and D=25 years, for x=4 pairs a probability of p=0.038 or 1 in 26. This is higher than we expected but not very high.
We can apply Martin's formula of course also to other tournaments. In the Corus Chess tournament of 2008 there was 1 pair in the A-group which gives p(x=1; D=23, n=14) = 0.056 or 1 in 18; in the B-group there were 5 pairs p(x=5; D=32, n=14) = 0.008 or 1 in 123; in the C-group there were 2 pairs p(x=2; D=19, n=14) = 0.091 or 1 in 11. We observe that the occurrence of one or more pairs with the same year of birth among 14 players is not unusual.
4. A remarkable chess tournament
In this section we have a look at the probabilities of certain chess tournaments and determine the circumstances for a remarkable one.
The probability p(n; x,y,D) that there are x y-tuples (pairs (y=2), triples (y=3), 4-tuples, etc.) among n chess players is given by
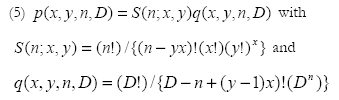
The S(n;x,y) represents the number of x y-tuples in a population of n players. The corresponding probability is given by q(x,y,n,D) under the assumption that all the birthdays (years of birth) are different and fall in a time span of D days (years).
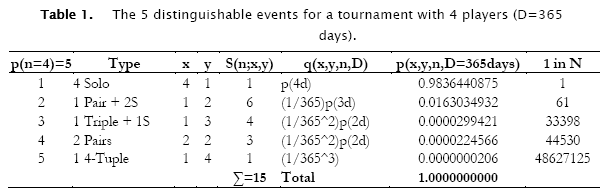
To get a feeling for formula (5) let's consider two situations. Let's start with the simple case of a tournament with n=4 players and let's have a look at their birthdays. In this case D = 365 days. There are 5 different events: all 4 players have different birthdays; there is 1 pair with the same birthday; there are 2 pairs with the same birthday; there is 1 triple with the same birthday; all 4 players have the same birthday. The probabilities of these events can be found in Table 1.
For this tournament we can make use of formula 5 for all five cases. We point out that p(4d) is the probability of having 4 different birthdays. In case of a pair we have to add the probability (1/365), in case of a triple (1/365)2 and in case of a 4-tuple (1/365)3. A nice feature of the probabilities is that they should add up to 1 which they indeed do.
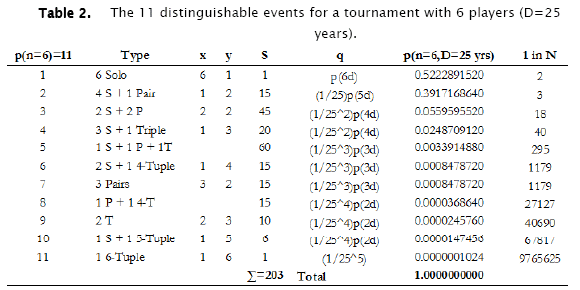
Let's have a look at the probabilities for a tournament with n=6 participants who were all born in a time span of D=25 years. There are 11 different events.
We observe that we can determine the probability p with formula 5 for 9 of the 11 events. For the corresponding values of x and y see Table 2. In case 8, i.e. 1 pair and a 4-tuple, the number S = [(6!/(2!4!)][4!/(4!0!)] = 15. We can find the probability p of this event by multiplying S=15 by the probabilities that belong to the years of birth of the pair (1/25) and the 4-tuple (1/25)3 and the probability that these 2 years of birth are different p(2d) = (24/25). In case 5, i.e. 1 pair, 1 triple and 1 solo we find S = [{(6!/(2!4!)} {4!/(3!1!)}] = 60. We can find probability p of this event by multiplying S=60 by the probabilities of the years of birth of the pair (1/25) and the triple (1/25)2 and the probability that there are 3 different years of birth p(3d)=(24/25)(23/25).
Looking at Table 2 we see that the remarkable tournaments are those with two triples (1 in 40690), one 5-tuple (1 in 67817) and, that very rare bird, the 6-tuple (1 in 9765625).
5. The partition numbers
In this section we illustrate from a different angle that probability is a rich part of applied mathematics. We observe that peculiar numbers appear in both tables. In order to identify these numbers we used Neil Sloane's 'On-Line Encyclopedia of Integer Sequences' [8]. We already know, from Tables 1 and 2, that p(n=4) = 5 and p(n=6) =11. In a straightforward way we found the p(n) sequence 1, 2, 3, 5, 7, 11, 15, 22, 30... which led to the so-called partition numbers. The sums of the S coefficients are 1, 2, 5, 15, 52, 203, 877,... and they appeared to be Bell numbers. After rearranging the S-numbers we discovered that they are multinomial coefficients. Suddenly we have entered a branch of pure mathematics that is concerned with the properties of numbers in general and integers in particular, i.e. number theory.
Let's have a closer look at the partition numbers. These numbers have been studied since the days of Leonhard Euler, one of the greatest mathematicians of all time. He discovered their main properties in 1,740 [9, 10]. Since then a lot of new discoveries have been made and even nowadays the partition function p(n) is still intensively being studied [11]. Our closer look will lead to the discovery of Euler's ship on the Pentagonal Sea and a new way of looking at the recurrence relation of the partition function and the pentagonal number theorem.
The following defining formula for p(n), with p(n,k) the number of partitions of n with the smallest term k, is the starting point for our investigations.
![]()
Looking at Table 3 we see that p(6,1)=7 , p(6,2)=2, p(6,3)=1 and p(6,6)=1. The sum of these four values is of course p(6)=11. Formula 6 led to the p(n,k) triangle, see Table 3 and [8].
As was also noted by Kevin Brown the p(n,1) partitions can be formed by appending 1 to each of the p(n-1) partitions of (n-1). The p(n,2) partitions can be formed by appending 2 to each of the p(n-2)-p(n-2,1) partitions of (n-2) whose smallest terms are at least 2. The p(n,3) partitions can be formed by appending 3 to each of the p(n-3)-p(n-3,1)-p(n-3,2) partitions of (n-3) whose smallest terms are at least 3, and so on. Of course there is also one partition of n with the smallest term n [12]. This leads to three relations for the values of the p(n,k) triangle.
These three relations enable us to construct the values of p(n). Start with p(n,n) = 1 and p(n,1) = p(n-1) and construct the intermediate values of p(n,k) with formula (9).
Thanks to formula (10) we can construct the following expressions for the p(n,k).
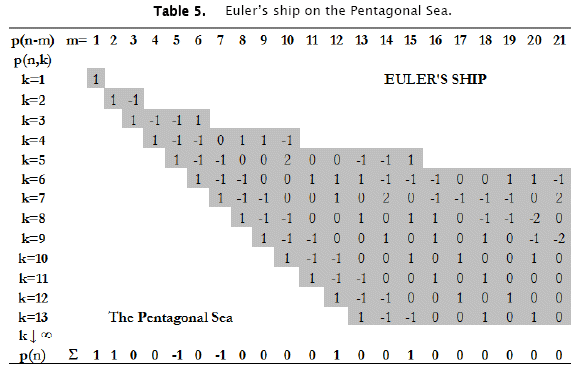
With the p(n,k) expressions we constructed the matrix of Table 5. It is this, apparently new, matrix that highlights some of the properties of the partition function p(n) in a remarkable way.
We observe that formula (6) leads for k to infinity to
![]()
which is Euler's recurrence relation for the partition function p(n), with p(0)=1 and p(n)=0 for negative values of n. The numbers 1, 2, 5, 7, 12, 15, 22, 26, .... are pentagonal numbers [8].
Formula (10) represents one interpretation of the horizontal rows. There is a second interpretation for these rows. Let's define
![]()
For k = 5 we have
![]()
which is the generating function of the values for p(n,5) in the fifth row of Table 5. Obviously fk(x) = fk-1(x) (1-xk-1) which implies that the construction of the fk(x) is based on the same rules as the ones that we used in Table 4 to construct the p(n,k). This leads us to the conclusion that the series expansions of the fk(x) generate the values in the rows of the matrix in Table 5 (k>1).
It is interesting to see that the structure of the p(n,k → ∞) in Table 5 leads us to Euler's famous pentagonal number theorem [11].
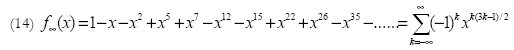
Two other aspects are worth mentioning. The number of row or deck entries 1, 2, 4, 7, 11, 16, etc.., are central polygonal numbers. The nickname of this sequence is the Lazy Caterer's sequence, because these numbers also represent the maximum number of pieces when slicing a pancake with k-cuts. The number of column or elevator entries 1, 1, 2, 2, 3, 4, 4, 5, 6, etc. form a sequence that is closely related to the Connell sequence. Amazingly, the terms of our sequence have a closed form a(n) = n+1-floor((1+sqrt(8n-7))/2), where floor(x) is the largest integer less than or equal to x [8].
Looking at Table 5 we recognize the contour of a ship that floats on a sea of numbers. We observe that in the structure of the lower decks the pentagonal number theorem appears while the sums of the numbers in the elevators lead to the recurrence relation of the partition numbers. Since it was Euler who discovered the relevant formulae we have named our ship after Euler and the sea of numbers has become the Pentagonal Sea.
It is nice to know that Euler started his career studying the masting of ships, i.e. how many masts to use and where in the ship to position the masts. A nineteen year old Euler wrote his essay on this problem in 1726, and when the results of the Paris Prize competition were published in 1728, he had won first prize. Throughout his career he kept a keen interest in ships and wrote two major books on this subject, including his last book, ScientiaNavalis, published in two volumes in 1773 [13].
6. A wager
What is probability theory without a wager? On April 13, 2008, one of us (JWM) got an invitation for a wager from the journalist who wrote a short article in the Dutch daily newspaper De Telegraaf about a 'Unique chess confrontation' on April 5, 2008, [6]. He offered to pay 10,000 if the unique chess confrontation between Smeets and l'Ami occurred again on April 5 during a Dutch Chess Championship. If it didn't happen again he wished to receive 1,000.
Should one accept or reject this offer? Until now Smeets and l'Ami have participated in three DCC's together. Both players are young and quite strong grandmasters. Smeets for instance went on to win the DCC of 2008 and Erwin l'Ami shared second place at the European Championship in Plovdiv in May 2008. If we, rather optimistically, assume that they'll participate another 25 times together, and equalize the present record of 28 held by International Grandmaster John van der Wiel, what is the probability that they will play each other again on their birthday? This situation represents a so-called Bernoulli trial and the probability of success can be calculated with the binomial distribution.
![]()
Although this probability is rather low we can't rule out that they will meet once again.
What does our rather optimistic assumption mean for the proposed wager? The probability of losing our stake is 0.93 and of winning his stake is 0.07. This leads to an expected gain of
![]()
The negative expected gain implies of course that the proposed wager should be rejected.
What could be considered a fair wager? Something that we have to take into account here is that many grandmasters abandon chess after a number of years. This is mostly due to lack of success and/or lack of money. Either Smeets or l'Ami could stop any day of any year which would mean the end of the wager. How does this influence our chances for success?
In probability theory there are two schools of thought: the orthodox and the Bayesian. Both schools treat each other with circumspect because the difference in philosophy between these two is, according to E.T. Jaynes, enormous [14]. Fortunately in many situations both schools reach the same conclusions so in general we don't have to worry too much. In some situations, like the one we have here, the Bayesian school can provide answers that the orthodox school can't, which might motivate the reader to have a closer look at the Bayesians!
We have the following probabilities for a DCC birthday meeting of Smeets and l' Ami
with p(N) the probability that both players still participate after N years and beyond that not anymore. Nmax is the number of DCC's that both players participate together. We assume that the probability distribution function (pdf) that a player leaves in the time span between 0 and Nmax is uniform and that the pdf s of the two players are mutually independent. It is in fact here that the Bayesian stance enters; the uniform distribution conforms best to what we know. Other distributions would assume more information. Under these circumstances it can be shown that p(N) is a linear function
In obtaining (19) we "juggled" a bit so as to be allowed to do an integration from 0 to N rather than a tedious summation over all integers up to N. The pdf is normalized so the integral of p(N) from 0 to Nmax is 1. This leads to
where we replaced the summation of (17) by integration, which simplified our work.
If we limit the duration of the wager to 10 years we should lower our stake to 100 while for a duration of 25 years it should be 200. In both cases the stake of the opponent remains 10,000. These stakes lead to an expected gain for both of approximately 0. A fair wager.
One of us (JWM) proposed a counter offer of 100 (50) bottles of wine against 1 bottle of wine. So far this offer hasn't been accepted.
7. Conclusions
We hope that it has become apparent that probability theory is a rich part of applied mathematics. Even simple concepts like coincident years of birth lead to fascinating discoveries. The most remarkable discovery was Euler's ship on the Pentagonal Sea. The elegant structure of Euler's ship provides new insight into the partition function and the pentagonal number theorem. We also showed how, within a Bayesian framework, one can decide whether a wager should be accepted or rejected in cases where we lack certain information. Something that might be useful for the reader in case (s)he is ever confronted with a proposal for a wager.
References
[1] Mathematics as an educational task. Hans Freudenthal. 1973.
[2] An introduction to probability theory and its applications. William Feller. 1966.
[3] The Monty Hall problem. en.wikipedia.org/wiki/Monty_Hall_problem. The correct answer is that it is to your advantage to switch doors. Few people do this.
[4] The exponential integral distribution. J.W. Meijer and N.H.G. Baken. Statistics and Probability Letters, pp. 209-211, Volume 5, no. 3, April 1987.
[5] Coincidences: Remarkable or Random. Bruce Martin. Skeptical Inquirer Magazine. Sept/Oct. 1998. www.csicop.org/si/9809/coincidence.html.
[6] ‘Unique chess confrontation’, Hans Bohm, De Telegraaf, April 5, 2008. In this article a probability of 1 in about 10 million was given for this event: a difference of a factor 200!
[7] Private communication. Prof. Bruce Martin, University of Virginia, Charlottesville, USA.
[8] The On-Line Encyclopedia of Integer Sequences. N.J.A. Sloane. Partition numbers (A000041). Bell numbers (A000110). Multinomial numbers (A036040). Pentagonal numbers (A001318). The p(n,k) triangle (A026794). Central polygonal numbers (A000124). Connell sequences (A001614; A122797). research.att.com/~njas/sequences/
[9] How Euler did it. Philip Naude’s problem. Ed Sandifer. October 2005. www.maa.org/editorial/euler/How Euler Did It 24 partitions.pdf
[10] Euler and the Pentagonal Number Theorem. Jordan Bell. http://arxiv.org/abs/math/0510054
[11] Addition and Counting: The Arithmetic of Partitions. Scott Ahlgren and Ken Ono. Notices of the AMS. Volume 49, Number 9. Oct. 2001. pp.978-984. www.ams.org/notices/200109/
[12] On Euler’s Pentagonal Theorem. Kevin S. Brown. 1994-2008. www.mathpages.com
[13] How Euler did it. Propulsion of Ships. Ed Sandifer. February, 2004. http://www.maa.org/editorial/euler/How Euler Did It 04 Propulsion of ships.pdf
[14] Probability Theory. The Logic of Science. E.T. Jaynes. Cambridge University Press. 2003.