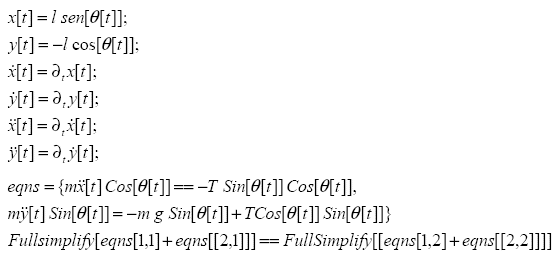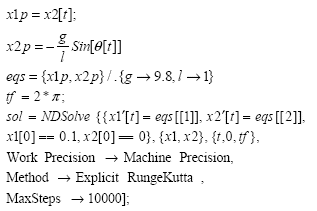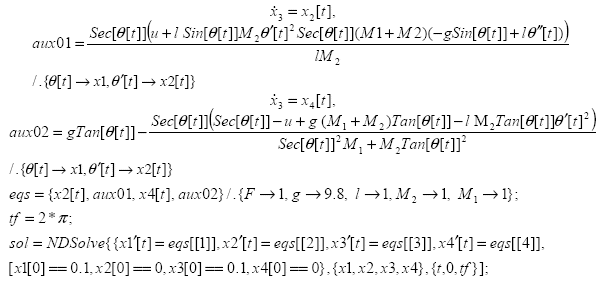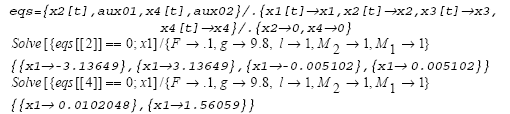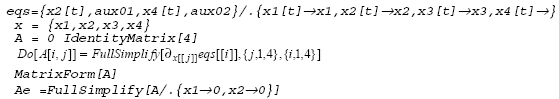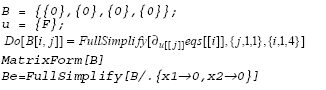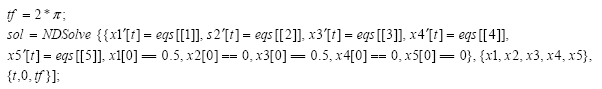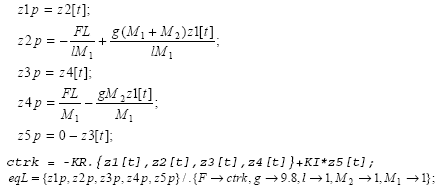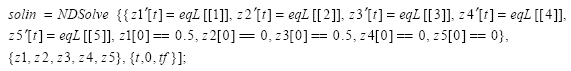Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Acta Nova
versión On-line ISSN 1683-0789
RevActaNova. vol.4 no.1 Cochabamba dic. 2008
Apunte
Modelado y simulación de sistemas utilizando MATHEMATICA®
Francisco Javier Triveño Vargas
Empresa Brasilera de Aeronáutica
e-mail: francisco.vargas@embraer.com.br
Resumen
El vertiginoso avance tecnológico en el que nos encontramos, ha establecido la necesidad de que las universidades recurran al uso de programas computacionales que permitan una continua mejora en su enseñanza tanto en ingeniería como en otras áreas. Es dentro de este contexto que el presente artículo tiene como objetivo la familiarización con el programa de computación simbólica MATHEMATICA®. Para alcanzar este objetivo el programa es empleado para obtener modelos no lineales, determinar puntos de equilibrio, obtener modelos lineales y finalmente simular el comportamiento de los modelos obtenidos. Los ejemplos en los cuales es utilizada la herramienta corresponden al péndulo ideal y al péndulo invertido.
Palabras clave: Computación Simbólica, MATHEMATICA®, Modelación, Simulación.
1 Introducción
MATHEMATICA® [8] es un paquete computacional que permite la realización de cálculos, obtención de soluciones y la visualización gráfica de las mismas, utilizando un lenguaje estrictamente simbólico. El programa en cuestión posee herramientas bastante poderosas para la representación de modelos matemáticos de un alto grado de complejidad, su solución numérica y la simulación de los mismos.
Teniendo en vista el creciente avance tecnológico y buscando un alto nivel de competitividad en el mercado profesional, diversas universidades en el mundo han introducido en sus programas de enseñanza el paquete MATHEMATICA® [3], lo que ha permitido aumentar el grado de comprensión de una amplia gama de problemas no solamente en ingeniería sino también en otras áreas [2].
Es en este sentido que el presente artículo tiene por objetivo la difusión del programa MATHEMATICA® como instrumento de modelado y simulación de sistemas mecánicos, abordando como caso de estudio el péndulo ideal y el péndulo invertido. Los resultados obtenidos, permiten mostrar y verificar de manera muy simple las ventajas de esta herramienta.
El artículo está organizado de la siguiente manera: en la sección 2 se presentan las ecuaciones para la obtención del modelo matemático del péndulo ideal y el péndulo invertido. En la sección 3 se obtienen los modelos matemáticos utilizando MATHEMATICA®. En la sección 4 se presentan los resultados del cálculo numérico y de simulación correspondientes a los dos modelos no lineales. En la sección 5 se describen y determinan los puntos de equilibrio de los dos modelos. En la sección 6 se presenta la expansión por series de Taylor para la obtención de modelos lineales y se obtiene el modelo lineal del péndulo invertido. En la sección 7 se presenta los resultados de simulación de los modelos lineal y no lineal del péndulo invertido, así como las comparaciones respectivas. Finalmente en la sección 8, se plantean algunas conclusiones.
2 Modelos Matemáticos
La mayoría de los fenómenos que se presentan en la naturaleza involucran la variación de una cantidad en relación a otra, llevando naturalmente a modelos matemáticos basados en ecuaciones diferenciales [6]. Estas ecuaciones son obtenidas empleando leyes como la segunda ley de Newton, la ley de conservación de energía o las leyes de Kirchhoff. A seguir, se detallan los modelos matemáticos del péndulo ideal y del péndulo invertido.
2.1 El péndulo ideal
El péndulo ideal se caracteriza por ser un cuerpo puntual de masa m que se mueve sobre la acción de la fuerza del peso y la tensión T que el hilo de suspensión de longitud l ejerce en la base donde se encuentra fijada. La figura 1 ilustra este problema.
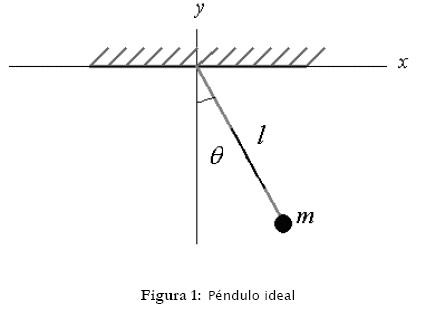
Escogiendo la base o el punto de suspensión del péndulo, como el origen de un sistema cartesiano, con el eje y positivo hacia arriba, las coordenadas (x,y) de la masa están relacionadas una a la otra a través de la ecuación x2 + y2 =1 . Por lo tanto es conveniente estudiar su movimiento en términos del ángulo θ que el hilo de suspensión del péndulo forma con el eje vertical. Por convención, θ > 0 cuando la masa se encuentra a la derecha del eje y y θ < 0 cuando la masa se encuentra a la izquierda. De esta forma las variables (x, y) del sistema de coordenadas son dadas por: x = lsenθ y y = -lcosθ (por tratarse del péndulo ideal, se desprecia la fricción).
Utilizando la segunda ley de Newton ![]() y separando los vectores en sus respectivos componentes se obtiene:
y separando los vectores en sus respectivos componentes se obtiene:
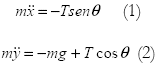
Multiplicando las ecuaciones (1) y (2) por cosθ y senθ respectivamente, se obtiene la ecuación no lineal del péndulo ideal (este modelo también puede obtenerse empleando otros métodos).
2.2 El péndulo invertido
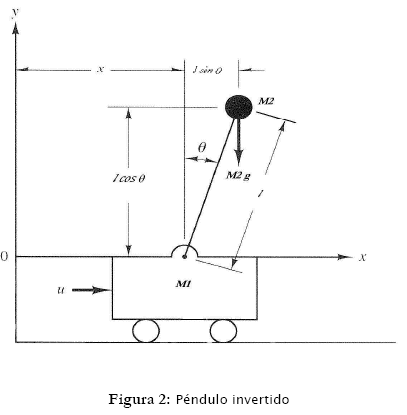
El péndulo invertido consiste en un carro de masa M1 que tiene adosada una varilla en cuyo extremo se encuentra un cuerpo de masa M2 . El carro puede moverse hacia delante o hacia atrás en línea recta, al aplicársele una fuerza u. La varilla está unida al centro del carro mediante una juntura, que le permite girar sobre un eje situado en la juntura y con un grado de libertad sobre el plano determinado por la dirección de movimiento del carro y la normal al suelo. La figura 2 ilustra el problema del péndulo invertido.
Al contrario del primer ejemplo, en este caso el modelo no lineal se obtiene empleando el método variacional a través de las ecuaciones de Lagrange [7].
![]()
donde L corresponde al Lagrangiano, T es la energía cinética y V la energía potencial.
Dada la ecuación de Lagrange, se define la siguiente función:
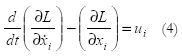
donde ![]() i y
i y ![]() i son las variables de posición y velocidad del péndulo [θ,
i son las variables de posición y velocidad del péndulo [θ,![]() ], [θ,
], [θ,![]() ], ui corresponde a las fuerzas externas actuando en el sistema relacionadas específicamente a u y a los efectos gravitacionales sobre M2 .
], ui corresponde a las fuerzas externas actuando en el sistema relacionadas específicamente a u y a los efectos gravitacionales sobre M2 .
Las energías cinética T1 y T2 de cada una de las masas del péndulo se definen como:
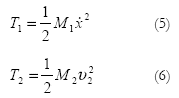
En la ecuación (6), v2 se define a partir de la posición horizontal ph = x + lsinθ y la posición vertical pv = lcosθ de M2 tal que:
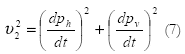
Las ecuaciones (3)-(7), permiten obtener el modelo no lineal del péndulo invertido.
3 Obtención de los modelos utilizando MATHEMATICA
3.1 Modelo del péndulo ideal
Con el auxilio de MATHEMATICA® y utilizando las ecuaciones (1) y (2), el modelo del péndulo ideal se obtiene de la siguiente forma:
![]()
La ecuación (8) corresponde a la ecuación no lineal del péndulo ideal. Haciendo x1= θ y x2 = ![]() la ecuación (8) en términos de variables de estado se describe como:
la ecuación (8) en términos de variables de estado se describe como:

3.2 Modelo del péndulo invertido
Con el auxilio de MATHEMATICA® y utilizando las ecuaciones (3), (4), (5), (6) y (7), el modelo del péndulo invertido es obtenido de la siguiente forma:
Observando las dos últimas líneas de código, las ecuaciones para ![]() y
y ![]() se definen como:
se definen como:
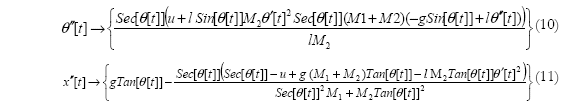
Las ecuaciones (10) y (11) corresponden al modelo no lineal del péndulo invertido [7]. Haciendo x1 = θ, x2 = ![]() , x3 = x y x4 =
, x3 = x y x4 = ![]() , las ecuaciones (10) y (11) son re escritas en variables de estado como:
, las ecuaciones (10) y (11) son re escritas en variables de estado como:
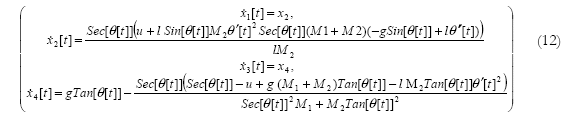
4 Simulación No Lineal - Resultados
Para realizar la simulación no lineal, se utilizan los modelos (9) y (12). Al mismo tiempo se deben considerar aspectos como el método de integración, precisión de cálculo y el número máximo de interacciones para la obtención de la solución [6].
4.1 Péndulo ideal
El cálculo numérico para la resolución de la ecuación (4) se realiza empleando la función NDSolve de MATHEMATICA®, de la siguiente forma:
En estas líneas, se puede observar que el intervalo de tiempo se define como {t,0,tf}, las condiciones iniciales corresponden a [x1→ 0.1, x2 → 0] y los valores de g, l son 9.8 y 1 respectivamente. En este punto es importante observar que MATHEMATICA provee otros métodos de integración, varía el número de interacciones y cambia la precisión de máquina por otras. Dependiendo de estas opciones, los resultados presentarán características diferentes, llevando en algunos casos a un atraso en el cálculo de la respuesta [8].
Una vez realizado el cálculo numérico es posible visualizar el comportamiento temporal de las respuestas obtenidas a través de las siguientes instrucciones:
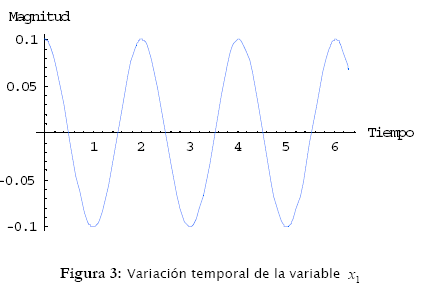
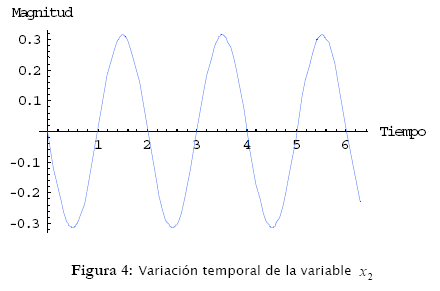
El comportamiento de las variables x1 y x2 está ilustrado en las figuras 3 y 4.
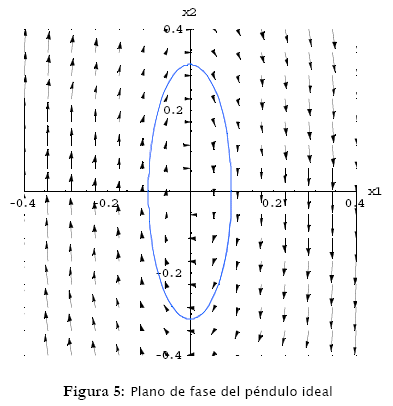
Adicionalmente, en estos resultados se puede observar que el péndulo ideal es un sistema periódico que no disipa energía, por lo que oscila de forma infinita. Estos resultados son reforzados a través del plano de fase y su respectivo campo de direcciones (el método de las isoclinas puede ser utilizado para este propósito). Estos resultados están ilustrados en la figura 5. Sus instrucciones son:
4.2 Péndulo Invertido
El cálculo numérico para la resolución de la ecuación (12), nuevamente se realiza utilizando la función NDSolve:
Nuevamente, el intervalo de tiempo está definido como {t,0,tf}, las condiciones iníciales corresponden a [x1 → 0.1, x2 → 0, x3 → 0.1, x4 → 0] y los valores de F, g, l, M2 y M1 son 1, 9.8, 1, 1 y 1 respectivamente. Realizado el cálculo numérico, el comportamiento en el tiempo puede ser visualizado través de las siguientes instrucciones:
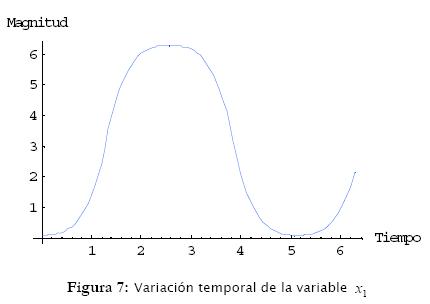
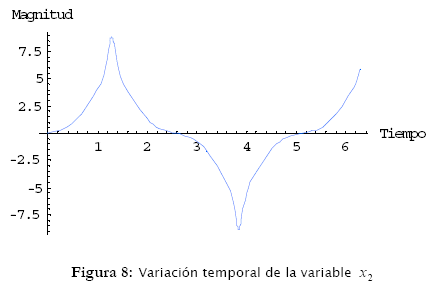
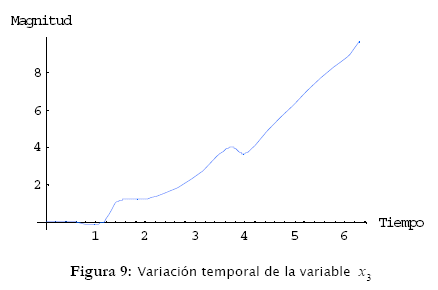
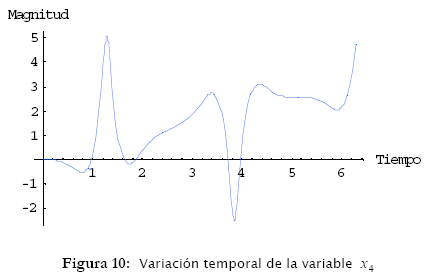
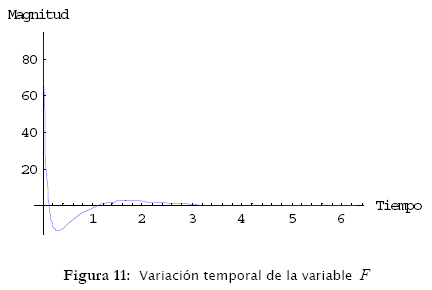
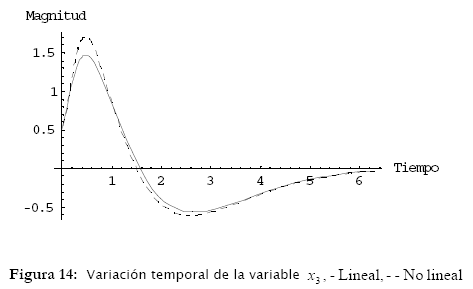
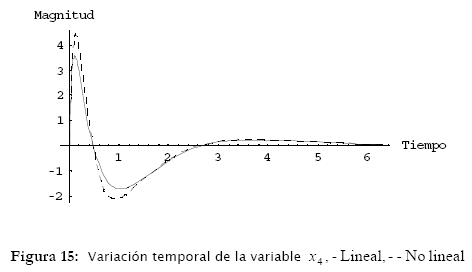
Los resultados de simulación están ilustrados en las figuras 6, 7, 8, 9 y 10.
En estos resultados se puede observar que las variables x1 = θ y x2 = ![]() tienen características periódicas para F constante (figuras 6, 7 y 8). Ya las variables x3 = x y x4 =
tienen características periódicas para F constante (figuras 6, 7 y 8). Ya las variables x3 = x y x4 = ![]() son crecientes en el tiempo y presentan inestabilidad (figuras 9 y 10).
son crecientes en el tiempo y presentan inestabilidad (figuras 9 y 10).
5 Puntos de Equilibrio
Un punto de equilibrio de un sistema ![]() = f(x,u,t) es un punto xeq, tal que
= f(x,u,t) es un punto xeq, tal que ![]() en este punto sea igual a cero, ya que en estas condiciones el sistema no cambiará de estado [5]. Considerando la ecuación (9) del péndulo ideal para que
en este punto sea igual a cero, ya que en estas condiciones el sistema no cambiará de estado [5]. Considerando la ecuación (9) del péndulo ideal para que ![]() 1 y
1 y ![]() 2 sean cero, es necesario que:
2 sean cero, es necesario que:
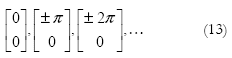
Este resultado muestra que el péndulo está en reposo sólo en la dirección vertical, bien sea hacia arriba o hacia abajo. Si es hacia abajo el ángulo es cero (igual a ± 2π, ± 4π) y si está hacia arriba el ángulo es π(igual a ±π, ±3π); en ambos casos la velocidad angular x2 es cero. La simplicidad que caracteriza al péndulo ideal lo describe como un problema trivial, lo cual no sucede con el péndulo invertido como será presentado a continuación.
5.1 Determinación de los puntos de equilibrio del péndulo invertido
Re-escribiendo la ecuación (12) y haciendo z = (x1, x2, x3, x4)T y u = F, se obtiene la siguiente igualdad matricial:
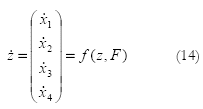
Los puntos de equilibrio se obtienen haciendo las derivadas de la ecuación (14) iguales a cero.
Aplicando MATHEMATICA® encima de la ecuación (12), se obtiene:
Para las variables especificadas, un punto de equilibrio corresponde a [x1 = 0, x2 = 0, x3 = 0, x4 = 0]. Adicionalmente como se puede observar, otros 2 puntos de equilibrio son identificados. Al contrario del péndulo ideal este problema ya presenta un cierto grado de dificultad, razón por la cual en lo sucesivo se abordará solamente este ejemplo.
6 Linealización del Modelo
Se pueden aplicar diferentes técnicas y aproximaciones a los modelos no lineales para obtener otros lineales. En el caso del péndulo ideal un modelo lineal es obtenido aproximado Sinθ ≈ θ, sin embargo no siempre es posible realizar este tipo de aproximaciones razón por la cual se debe recurrir a métodos formales. Para alcanzar este propósito, uno de los métodos más usados de linealización corresponde a la expansión por series de Taylor [1], [4]. Este método es bastante efectivo para pequeñas variaciones en las variables de estado con relación al punto de equilibrio. A continuación se realiza un resumen del método.
6.1 Expansión en series de Taylor
Siendo que el punto de equilibrio está dado por (zeq, Feq) y que la diferencia para pequeñas variaciones del vector de estados y entrada está dada por:
![]()
y
![]()
El lado derecho de la ecuación (17) se puede expandir utilizando las series de Taylor de la siguiente forma:
Los términos de orden elevado contienen cantidades de Δz y ΔF elevadas al cuadrado; como los valores de Δz y ΔF son pequeños, estas cantidades pueden ser despreciadas. Con esta consideración, se obtiene la siguiente aproximación:
Las derivadas parciales de la ecuación (19) corresponden a los Jacobianos [5] y son descritos a seguir:
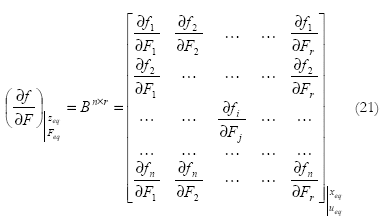
El sistema linealizado alrededor del punto de equilibrio está dado por
![]()
Finalmente haciendo ΔF = u y Δz = z, la ecuación (22) puede ser re escrita como:
![]()
donde A y B están dadas por las ecuaciones (20) y (21).
6.2 Obtención del modelo lineal del péndulo invertido con MATHEMATICA
Las matrices A y B junto con el modelo lineal se obtienen de la siguiente manera:
De tal forma que la matriz A en el punto de equilibrio está dada por:
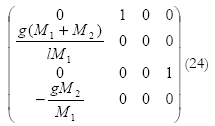
La matriz B en el punto de equilibrio está dada por:
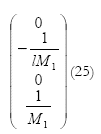
En la literatura clásica, las ecuaciones (24) y (25) se presentan directamente para su uso en diferentes aplicaciones [4].
7 Simulación lineal y no lineal del péndulo invertido - Resultados
Para obtener los resultados del modelo lineal representado por las ecuaciones (24) y (25) y compararlos con el modelo no lineal (12), el modelo no lineal se re escribe como:
El cálculo numérico se escribe como:
Ahora re-escribiendo el modelo lineal:
Y resolviéndolo numéricamente como:
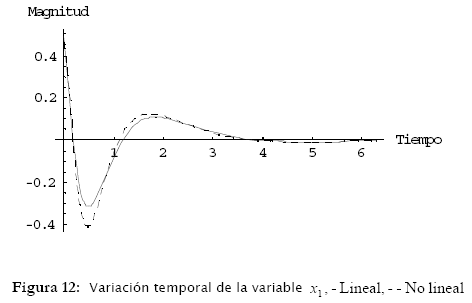
Finalmente los resultados pueden ser visualizados como:
En estos resultados es posible observar que la diferencia entre el modelo no lineal (línea punteada) y el modelo lineal (línea sólida) es mínima para pequeñas variaciones de las variables de estado. Esta diferencia es más evidente durante el régimen transitorio y no así en el régimen permanente. La obtención de estos modelos, su análisis y simulación permiten que los mismos sean utilizados para diferentes aplicaciones en ingeniería y otras áreas [9], [10].
8 Conclusiones
En este artículo se presenta y utiliza el paquete de computación simbólica MATHEMATICA®. A través de los resultados obtenidos se ha comprobado su robustez y versatilidad.
Para alcanzar el objetivo propuesto MATHEMATICA® ha sido empleado en la modelación de sistemas mecánicos, su resolución numérica y la simulación de los mismos. Fue aplicado al caso del péndulo ideal y del péndulo invertido, los resultados alcanzados fueron satisfactorios.
Además de los resultados presentados en este trabajo, con el objetivo de difundir el uso de la herramienta, algunos cursos ya fueron patrocinados por algunas universidades [9] y por la Sociedad de Ingenieros de Bolivia [10].
Finalmente se pretende dar continuidad al objetivo de modernizar la enseñanza en nuestro medio otorgando a través de ésta y otras herramientas un alto grado de madurez tanto a alumnos como a profesores de las diferentes áreas.
Referencias
[1] A. J. Jordan. 2006. Linearization of Non-linear State Equation. Bulletin of the Polish Academy of Sciences, Vol. 54, Nº 1
[2] L. Kovacs, B. Benyo, B. Palancz and Z.Benyo. 2004. A Fully Symbolic Design and Modeling of Non-Linear Glucose Control with Control System Professional Suite of Mathematica (CSPS). .Acta Physiologica Hungarica, Vol. 91, Nº 2
[3] Jose Manuel Gutierrez and Andres Iglesias. 1998. Mathematica Package for Analysis and Control of Chaos in Non-Linear Systems. Computer in physics, Vol. 12, Nº6
[4] Katsuhiko Ogata. 1997. Engenharia de Controle Moderno, Prentice Hall [ Links ]
[5] Khalil H. K. 1996. Non Linear Systems. Prentice Hall [ Links ]
[6] Junior E. C. y Penney D. E. 1995. Equações Diferenciais Elementares com Problemas de Contorno. Prentice Hall do Brasil
[7] William A. Wolovich. 1994. Automatic Control Systems: Basic Analysis and Design. Oxford University Press [ Links ]
[8] http://www.wolfram.com/ [ Links ]
[9] Vargas F. J. T. 2007. Curso de Extensión: Modelaje, Simulación y Control de Sistemas. Universidad del Valle, Cochabamba [ Links ]
[10] Vargas F. J. T. 2006. Curso Externo: Control a Estructura Variable y Modos Deslizantes. Sociedad Boliviana de Ingenieros, SIB, Cochabamba [ Links ]