Artículo científico

 

Aplicación de la inteligencia artificial a la resolución del problema de asignación de estudiantes del departamento de PDI

 

 

Ricardo Köller Jemio

Departamento de Ciencias Exactas e Ingeniería, Universidad Católica Boliviana

e-mail: ricardo.koller@jalasoft.com

 

 

---

Resumen

En este artículo se examina la aplicación de la Inteligencia Artificial a la resolución del Problema de Asignación de Estudiantes del departamento de Práctica Docente e Investigación (PDI) del Instituto Normal Superior Católico Sedes Sapientiae (INCSS). Se muestra cómo se ha resuelto el problema, modelándolo como Problema Sujeto a la Satisfacción de Restricciones Parciales (PCSP por sus siglas en ingles) y Búsqueda Local Guiada (GLS por sus siglas en inglés) como algoritmo de búsqueda. Luego, se muestran los resultados obtenidos y algunas conclusiones respecto al problema, algoritmos de búsqueda local y a GLS en general.

Palabras clave: Inteligencia Artificial, CSP, búsqueda local, GLS, NP-completo.

---

 

 

1    Introducción

El Problema de Asignación de Estudiantes del departamento de PDI, que llamaremos PAEP en este articulo [1], trata con la asignación a estudiantes de recursos limitados. Esta asignación debe tomar en cuenta diferentes restricciones y preferencias. Las restricciones limitan el conjunto de asignaciones posibles a un sub-conjunto y las preferencias son criterios de elección entre asignaciones de este sub-conjunto. Muchos problemas de este tipo pertenecen a una clase de problemas que presenta una enorme dificultad a los desarrolladores de algoritmos.

Las técnicas descritas en este artículo pueden ser usadas en problemas de asignación similares. En general, estas técnicas pueden ser aplicadas a un tipo más amplio de problemas conocido como Problemas Sujetos a la Satisfacción de Restricciones Parciales (PCSP). Los PCSP son una extensión a los Problemas Sujetos a la Satisfacción de Restricciones (CSP) y permiten modelar problemas de optimización que, además, están sujetos a la satisfacción de restricciones.

 

2    El Problema de Asignación de Estudiantes (PAEP)

Todos los estudiantes del INSCSS deben tomar materias de práctica llamadas PDI. Existe una de estas materias para cada semestre y especialidad. Las materias PDI tienen como objetivo, entre otros muchos, que los estudiantes realicen prácticas docentes en unidades educativas de la región. Un departamento específico de la INCSS, llamado PDI, tiene como tarea organizar, seguir y evaluar estas prácticas. Las tareas de organización incluyen agrupar a los alumnos para realizar prácticas y asignar un colegio a cada grupo de acuerdo a una serie de restricciones y preferencias. Cada grupo es seguido y evaluado por el docente de su materia PDI, quien visita regularmente a los estudiantes en los colegios donde practican Un grupo de visita está formado por alumnos de la misma materia y su tamaño depende del semestre. La asignación de colegios a grupos de visita es el Problema de Asignación de Estudiantes del departamento de PDI (PAEP).

Se ha demostrado que este problema pertenece a la clase de problemas NP-completos, gracias a una reducción polinomial a partir de otro problema NP-completo llamado 3-CNF satisfiability. La demostración puede ser encontrada en [1]. Parece no existir una manera de resolver este problema en tiempo polinomial y por tanto lo único que puede esperarse es una solución que se aproxime lo más posible a la mejor solución.

 

3    Modelamiento del PAEP

A continuación se modelará el PAEP como un Problema Sujeto a la Satisfacción de Restricciones Parciales (PCSP). Para esto se definen las restricciones duras (restricciones que no pueden ser violadas), las restricciones blandas (restricciones que pueden ser violadas a un costo determinado), las preferencias y una función objetivo, que es el indicador principal de hasta qué punto es buena una asignación. La solución a este problema consiste en encontrar la asignación para la cual se tiene el menor valor de la función objetivo, sin violar ninguna restricción dura. Este modelo está basado en el trabajo realizado por Voudoris y Tsang para el problema de asignación de frecuencias [3].

3.1 Restricciones duras

Se tiene un conjunto G de grupos de alumnos y un conjunto D de dominios para cada grupo.

Para todo grupo i, una unidad educativa u_i debe ser escogida del dominio D_i lo que es la primera restricción dura del PAEP.

En el PAEP, algunas restricciones duras pueden ser obviadas de la búsqueda al restringir los dominios antes de iniciar el algoritmo. Estas restricciones son:

a) Existen grupos con un colegio pre-asignado.

b) Existen grupos a los cuales no les pueden ser asignados ciertos colegios.

c) Grupos que deben tener asignados colegios de cierta zona de la ciudad.

Hay una restricción dura que no puede ser aplicada a la búsqueda de la solución restringiendo el dominio. Se trata del limite en el número total de estudiantes recibidos por unidad educativa. Para esta restricción tenemos el siguiente modelo:

Donde:

U es el conjunto total de unidades educativas asignables,

N_i es el número máximo de alumnos practicantes aceptados por la unidad educativa i, y

δ(condición) es 1 si la condición entre paréntesis es verdadera y 0 en caso contrario.

3.2 Restricciones blandas

Existe una restricción blanda relacionada al número máximo de estudiantes recibidos por especialidad en cada unidad educativa. Todo colegio puede recibir practicantes para diversas especialidades, por ejemplo tres alumnos practicantes para matemáticas y dos para historia. Se debe tratar que los números de practicantes por especialidad no sobrepasen esos límites, ya que de hacerlo, los estudiantes tendrán que hacer prácticas en especialidades que no son las suyas lo que es inaceptable. El número de violaciones a esta restricción blanda debe ser minimizado, por lo que el primer componente de la función objetivo es:

Donde:

C_u es el costo por violar la restricción de limitación por especialidad para la unidad educativa u,

Eg_g es la especialidad del grupo g,

Ec_u,e es el numero máximo de estudiantes aceptados por la unidad u y especialidad e, y

δ(condición) es 1 si la condición entre paréntesis es verdadera y 0 en caso contrario.

3.3 Preferencias

El departamento de PDI quiere minimizar la distancia entre todos los colegios asignados a grupos de cada docente. Esta es una preferencia que da lugar al segundo componente de la función objetivo y es definida de la siguiente manera:

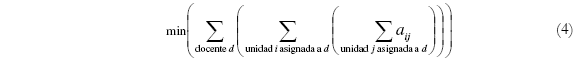
Donde:

a es una matriz n x n de distancias.

Otra preferencia, que llamaremos preferencia entre asignaciones, consiste en minimizar la suma de los indicadores de todos los colegios asignados. El indicador de un colegio es igual a la suma ponderada de una serie de características. Estas hacen que se prefiera un colegio en relación a otro. Por ejemplo, el tipo de establecimiento, nivel de cobertura, programa que desarrolla. Esta preferencia da lugar al último componente de la función objetivo:

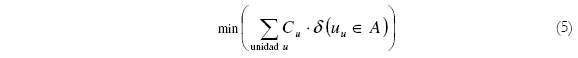
Donde:

A = es el conjunto de unidades educativas asignadas a al menos un grupo

C_u es el indicador de la unidad educativa u, y

δ(condición) es 1 si la condición entre paréntesis es verdadera y 0 en caso contrario.

3.4 Función objetivo

La función objetivo se calcula a partir de la cantidad de violaciones a restricciones blandas y de la consideración de preferencias de un estado determinado. El PAEP consiste en encontrar una asignación que minimice la función objetivo, la cual se define como la suma de (3), (4) y (5), y que cumpla las restricciones (1) y (2).

 

4    El algoritmo de búsqueda en el espacio de estados

El PAEP está modelado como un PCSP, por lo que la resolución a este problema es una búsqueda en espacio de estados. Cada estado representa una asignación completa y las aristas, posibles transformaciones de una asignación a otra. El algoritmo de búsqueda usado será Búsqueda Local Guiada (GLS) [2] que aprovecha información heurística específica de los problemas para escapar de los mínimos locales. Para trabajar, GLS usa un algoritmo de búsqueda local simple que en este trabajo será min-conflicts.

Min-conflicts empieza la búsqueda inicializando todas las variables con valores aleatorios de sus dominios. Luego, realiza una serie de transformaciones entre asignaciones completas hasta llegar a un mínimo local. En el PAEP una transformación consiste en la modificación del valor de una sola variable. La variable se escoge siguiendo un orden arbitrario estático y el nuevo valor que se le da es aquel que produce un resultado menor para la función objetivo.

La Búsqueda Local Guiada [2] es un algoritmo que tiene como objetivo ayudar a un algoritmo de búsqueda local simple a escapar de los mínimos locales. GLS ejecuta un algoritmo de búsqueda local simple un número definido de veces, de tal manera que la asignación resultante de una ejecución sea la entrada de otra. Las búsquedas simples terminan sus ejecuciones al alcanzar un mínimo local. Es en este instante cuando GLS ayuda a escapar del mínimo local mediante cambios en la función objetivo. Al hacer esto, GLS guía la búsqueda hacia mejores áreas del espacio de estados.

Al implementar GLS se deben definir una serie de características de la solución (conocidas como "solution features"). Una característica es cualquier propiedad no deseada de la solución; cualquier solución puede o no tener una determinada característica. Por ejemplo, una característica en el Problema del Coloreo de Grafos puede ser "Los nodos X y Y usan el color A". También se debe asociar cada característica con un costo. Estos costos son los que definen el valor de la penalización por característica. Cada vez que el algoritmo de búsqueda local simple alcanza un mínimo local, GLS aumenta la función objetivo con una penalización por cada característica presente.

 

5    Implementación de la solución

A la hora de implementar GLS con la función objetivo definida para el PAEP, existe un problema. Las restricciones de limitación por capacidad de colegios crean un espacio de estados lleno de mínimos locales profundos de los cuales es muy difícil escapar incluso para GLS. Por esta razón, estas restricciones se implementaron de tal manera que los costos por violación no sean igual a C_u, sino a C_u*exceso. Esta es la nueva versión del componente (3):

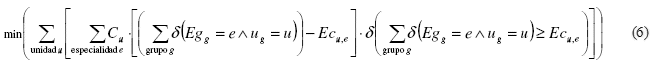
Donde:

C_u es el costo por violar la restricción de limitación por especialidad para la unidad educativa u,

Eg_g es la especialidad del grupo g,

Ec_u,e es el numero máximo de estudiantes aceptados por la unidad u y especialidad e, y

δ(condición) es 1 si la condición entre paréntesis es verdadera y 0 en caso contrario.

De esta manera se crea un espacio de estados menos accidentado en el cual se pueda definir un conjunto de características que sean eficaces a la hora de escapar de los mínimos locales. Las restricciones limitantes en el número de alumnos aceptados son muy importantes y pueden ser usadas para definir un conjunto básico de características: cada restricción de espacio es interpretada como una característica y cada violación a una de estas restricciones es interpretada como caracteristica presente.

El segundo conjunto de características trata de maximizar la cantidad de grupos asignados al mismo colegio y minimizar la cantidad de plazas no ocupadas en los colegios. Esta característica está presente para todo colegio al cual se le asigna al menos aun grupo.

 

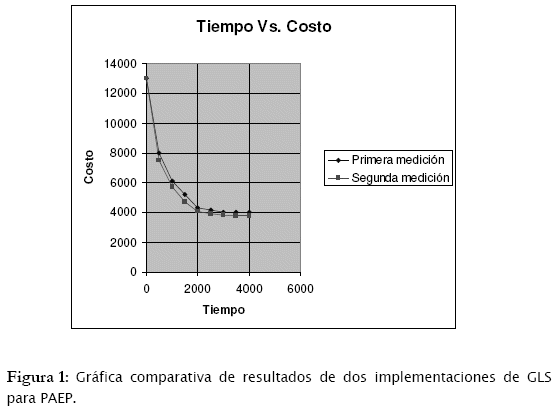
6    Resultados experimentales

La figura 1 muestra el valor de la función objetivo durante la ejecución de dos implementaciones del algoritmo. La primera implementación trata de escapar de los mínimos locales usando una serie de características basadas en las que fueron usadas para resolver el problema de asignación de frecuencias [3]. La segunda implementación usa la mejor combinación de las características definidas en el apartado anterior. Todas las ejecuciones se realizaron sobre el PAEP con 10000 grupos de estudiantes y 10000 colegios empezando de la misma asignación completa aleatoria.

La primera ejecución muestra claramente una reducción rápida que se vuelve cada vez más lenta hasta chocarse con la barrera de las 4000 unidades de costo. En la última ejecución se ve la misma tendencia, excepto que los resultados mejoran ligeramente. La mejora es de aproximadamente 100 unidades de costo.

Los primeros mínimos locales se encontraron a los 2000 segundos. Particularmente en este problema, se observó que pocos segundos después de haber alcanzado el primer mínimo local, el algoritmo podía hacer muy poco por mejorar el costo. También es interesante observar que la barrera empieza después de haber encontrado el primer mínimo local. Pueden verse estas asignaciones finales como mesetas dentro del espacio de estados.

La meseta de asignaciones finales alcanzada en nuestro problema durante cada búsqueda puede significar dos cosas: que realmente no exista una mejor solución o que el algoritmo no pueda escapar de la meseta de mínimos locales. Para tratar de responder esta pregunta se realizó el siguiente experimento:

Se creó una pequeña instancia de un PCSP (parecido al PAEP) con muchas mesetas y una zona especial con costos muy bajos. El problema consistía en encontrar la asignación óptima de 50 estudiantes a 50 colegios con soluciones conocidas de antemano, algunas muy buenas y grupos de soluciones con costos similares. Se ejecutó una implementación de GLS 100 veces con un límite de 10 mínimos locales en cada corrida. Sólo el 5% de las ejecuciones llegaron a las mejores soluciones y el 95% se quedaron en la meseta.

 

7    Conclusiones

Las características de la solución (conocidas como "solution features" en GLS) cambian el paisaje de estados, aumentando nuevos puntos de vista para que el algoritmo pueda encontrar una mejor alternativa al mínimo local. Sin embargo, viendo los resultados del segundo experimento se puede concluir que GLS no siempre impulsa los saltos a otras áreas del espacio de estados, por lo cual el algoritmo no puede escapar fácilmente de mesetas ni de mínimos locales.

No hay forma de saber cuándo una solución encontrada por este método está "cerca" de la mejor solución que existe, ni cuál de una serie de soluciones encontradas es la mejor, por un medio que no sea la simple comparación de los mejores valores de la función objetivo alcanzados en cada una de ellas.

 

Referencias

[1] Álvarez, Julio César; Köller, Ricardo; Tadic, Ivo. Sistema de apoyo al Departamento de Práctica Docente e Investigación del Instituto Normal Superior Católico Sedes Sapientiae. Universidad Católica Boliviana, 2005.        [ Links ]

[2] Voudouris, Chris; Tsang, Edward. Guided Local Search. http://citeseer.ist.psu.edu/cache/papers/cs/3444/http:zSzzSzcswww.essex.ac.ukzSzCSPzSzpaperszSzCSM-247.pdf/voudouris95guided.pdf.Technical Report CSM-247, 1995.

[3] Voudouris, Chris; Tsang, Edward. Solving the Radio Link Frequency Assignment Problem using Guided Local Search. http://cswww.essex.ac.uk/CSP/papers/VouTsa-Rlfap-Nato98.pdf. Department of Computer Science, University of Essex, 1998.