Artículo científico

 

Aplicación del método "Dual Boundary" para el cálculo de los parámetros de la mecánica de fractura elástica lineal de probetas tipo SE(T), DE(T) y M(T).

 

 

Ivan Aguirre¹, Itamar Ferreira²

¹Universidad Privada Boliviana,
²Universidad de Campinas

e-mail: iaguirre99@yahoo.com

 

 

---

Resumen

En aplicaciones de la Mecánica de Fractura, el método de Elementos de Borde ("Boundary Element Method") es un método numérico que tiene ventajas comparado con el método de Elementos Finitos; sin embargo, su difusión está aún muy restringida a pesar de ser una técnica suficientemente madura. El parámetro de campo K_I (factor de intensidad de tensiones en modo I), es el principal parámetro de la mecánica de fractura elástico lineal. Para el modelado por elementos de Borde de una fisura aguda es necesario usar técnicas especiales para evitar el aparecimiento de matrices singulares, en este trabajo se utilizó el método "Dual Boundary" en modelado bidimensional para materiales isotropicos, los factores de intensidad de tensiones fueron estimados usando el método "crack tip opening displacement" (desplazamiento de abertura de la punta de la fisura). Los tipos de probetas modelados fueron "Single Edge Notch Tension", SE(T), "Double Edge Notch Tension", DE(T), y "Middle Tension", M(T). Los resultados obtenidos muestran una buena correlación con los resultados analíticos y con los relatados en la literatura.

Palabras clave: DE(T), SE(T), M(T), Factor de intensidad de tensiones KI, "Dual Boundary"

---

 

 

1    Introducción

El parámetro de campo más importante de la mecánica de la fractura elástica lineal es el factor de intensidad de tensiones K. La mayoría de las metodologías para determinar el comportamiento y la tolerancia de las partes estructurales a las fisuras sin que acontezcan fallas catastróficas están basadas en la determinación del factor de intensidad de tensiones en la punta de la fisura.

Los dos métodos numéricos más usados en aplicaciones de ingeniería para analizar y modelar problemas estructurales complejos son el método de los Elementos Finitos - FEM y el método de los Elementos de Contorno — BEM, también conocidos como Elementos de Borde. Una de las principales ventajas del FEM es su amplia difusión, existiendo aplicaciones comerciales prácticamente para todas las áreas de las ciencias, al contrario, el BEM tiene su difusión muy restringida, existiendo pocos programas comerciales basados en este importante método.

Uno de los principales atractivos del BEM es que en su formulación numérica, cuando no existen fuerzas de volumen o de cuerpo, no es necesario integrar el dominio, procediéndose al análisis únicamente del contorno del problema, lo que permite disminuir la complejidad del problema en una dimensión; sin embargo el costo computacional que se paga por esta ventaja puede ser bastante elevado, porque en la aplicación discretizada del método aparecen matrices llenas y con singularidades que necesitan de técnicas especiales para su tratamiento. Existen reportes en la literatura especializada de que en el análisis numérico de problemas de la Mecánica de Fractura el BEM lleva a resultados más precisos [2].

Para el modelado de fisuras por BEM no es posible usar el método convencional, porque aparecen matrices mal condicionadas, una alternativa recientemente desarrollada para este tipo de problemas es la aplicación del método "Dual Boundary" [7].

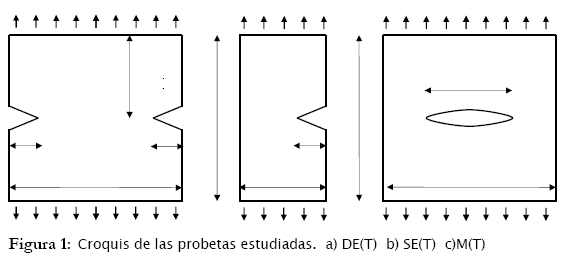
En este trabajo, para probetas tipo M(T), SE(T) y DE(T) mostradas en la Fig. 1, se calcula el factor de intensidad de tensiones para solicitaciones de la fisura en modo de abertura - K_I (modo I), usándose el método de los elementos de contorno dual ("Dual Boundary Method"), en análisis bidimensional, los resultados obtenidos son comparados con los relatados en la literatura especializada.

2    Formulación

Considerando una placa plana de tamaño y forma arbitrarios, con solicitaciones mecánicas en el estado plano y conteniendo una fisura aguda de orientación y tamaño cualquier, el campo de tensiones alrededor de la punta de la fisura puede ser expresada de forma aproximada por una expansión de la formula:

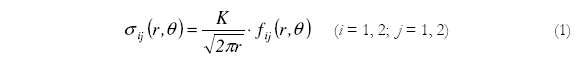
En esta ecuación, σ_ij es el tensor de tensiones en un punto del material posicionado a la distancia r de la punta de la fisura y a un ángulo de orientación θ a partir del plano de la fisura, f_ij son funciones trigonométricas conocidas. Una consecuencia importante de la Ec. (1) es que la distribución de tensiones alrededor de la punta de una fisura aguda es similar para cualquier estructura con el mismo factor de intensidad de tensiones, y depende apenas de los parámetros r e θ. Por tanto, el factor de intensidad de tensiones sirve como un factor de escala para definir la magnitud de las tensiones alrededor de la punta de una fisura. Este factor es función del tamaño de la fisura, del tipo de cargamento y de la configuración geométrica de la estructura o parte mecánica fisurada. Una hipótesis fundamental de la Mecánica de Fractura Elástica Lineal es que el comportamiento de la fisura es determinado estrictamente por los factores de intensidad de tensiones.

El procedimiento analítico usual de cálculo de K_I para configuraciones geométricas comunes está basado en la determinación de un factor base K₀ definida por la Ec. (2).

Donde ɑ es la longitud de la fisura. K_I ahora puede ser determinado por la aplicación de la Ec. (3).

Donde la función geométrica correctora F_I es dependiente del ancho de la sección W y de la longitud de la fisura, esta función puede ser encontrada en manuales especializados.

2.1 Elementos de Contorno

En la implementación del método de elementos de contorno es necesario usar soluciones fundamentales; para elasticidad plana, estas soluciones son conocidas como soluciones de Kelvin, dadas en la Ec. (4) para desplazamientos y en la Ec. (5) para fuerzas de superficie.

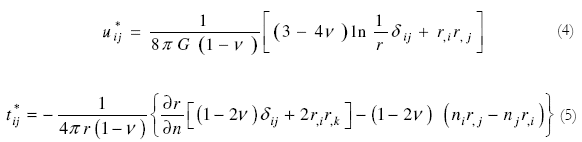
En estas ecuaciones: G = E/(2(1 + v)) (módulo de elasticidad transversal), E es el módulo de elasticidad longitudinal, v es el coeficiente de Poisson, n es la normal externa al contorno, r es la distancia del punto fuente al punto campo, y δ_ij es el delta de Kronecker. Los índices i,j,k para el estado plano asumen los valores de 1 y 2.

Aplicando el teorema de Betti y la identidad de Somigliana en combinación con las soluciones fundamentales, puede deducirse la Ec. integral (6) base del método directo de elementos de contorno.

Donde t_i son los vectores de fuerzas de superficie, u_i son los vectores de desplazamientos, b_i son los vectores de fuerzas de cuerpo o volumen y c_ij son las constantes del método cuyo valor depende de la posición del punto fuente con relación al contorno Γ. La Ec. (6) en su versión discretizada y desconsiderando la acción de fuerzas de cuerpo está representada por la Ec. (7), ecuación que es conocida como ecuación de desplazamientos del método de elementos de contorno.

La Ec. (7) es aplicada a cada uno de los nodos de los n_e elementos del contorno modelado, permitiendo la obtención de un sistema lineal que puede ser escrito en forma matricial como:

Donde las matrices H y G contienen respectivamente los valores de las integrales de las soluciones fundamentales de fuerzas de superficie t_ij y de desplazamientos u_ij, los vectores t y u contienen todas las fuerzas de superficie y desplazamientos conocidos o no. A través de algunas operaciones algebraicas puede ponerse en evidencia a las incógnitas en un vector f de forma que el sistema de la Ec. (8) puede ser reescrito como:

El sistema lineal representado por la Ec. (9) tiene solución única para problemas bien planteados.

2.2 Método de los Elementos de Contorno Dual (Dual Boundary Method -DBM)

Este método aplicado a problemas de fractura se basa en la aplicación de dos integrales de contorno diferentes en la fisura para evitar la formación de matrices singulares en la aplicación del método BEM en estructuras con fisuras, permitiendo que las fisuras puedan ser modeladas como una única línea. La ecuación integral de desplazamientos — Eq. (9) es aplicada para modelar todo el contorno analizado, incluyendo la fisura (uno de sus lados), posteriormente una segunda ecuación integral (ecuación de fuerzas de superficie) es aplicada al otro lado de la fisura. De tal forma que los nodos de los elementos de la fisura (considerados opuestos), que tienen las mismas coordenadas geométricas serán integradas por ecuaciones diferentes, lo que impide la formación de matrices mal condicionadas.

La ecuación de fuerzas de superficie se obtiene de la derivación de la ecuación de desplazamientos y esta representado por:

Donde: n_i es la normal externa al contorno, S_ijk y D_ijk están representados por:

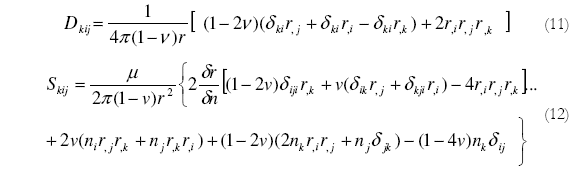
La ecuación integral de desplazamientos presenta una singularidad del tipo fuerte que puede ser tratada por la cuadratura de Gauss. La ecuación integral de fuerzas de superficie presenta hiper-singularidad, que es tratada por el método de sustracción de singularidades, en la implementación de esta solución, es necesario usar elementos discontinuos, y únicamente pueden ser modeladas fisuras rectas.

2.3 Determinación de K_I por Elementos de Contorno

La técnica aplicada en este trabajo para el cálculo de K_I partiendo de datos obtenidos por el método de Elementos de Contorno es la de desplazamientos de los nodos de la punta de la fisura ("crack tip opening displacement"). Los desplazamientos asociados a la Ec. (1) son [7]:

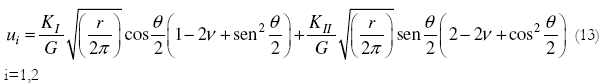
Para el modo I y considerando que en la punta de la fisura los desplazamientos son muy pequeños, la Ec. (13) puede rescribirse como:

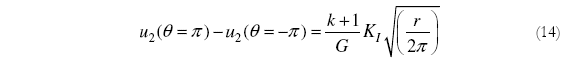
Donde k = 3-4v para deformación plana y k = (3-v) / (1+v) para tensión plana. Para el punto medio del elemento de la punta de la fisura n_pt, r es igual a la mitad de la longitud de n_pt (L_pt/2), sustituyendo este valor en la Ec. (14) y despejando el valor de K_I tenemos:

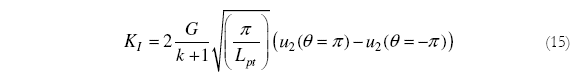
La Ec. (15) puede ser reescrita para cualquier otro punto perteneciente al elemento de la punta de la fisura. También es posible aplicar la Ec. (15) a dos puntos distintos del elemento de la punta de la fisura, aplicar mínimos cuadrados para minimizar el error y llegar a la Ec. (16).

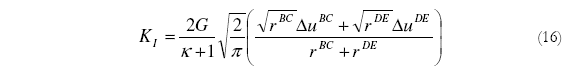
Donde el parámetro r es la distancia de la punta de la fisura hasta el punto o nodo del elemento de la punta de la fisura donde se esta midiendo el desplazamiento u (ver Fig.2).

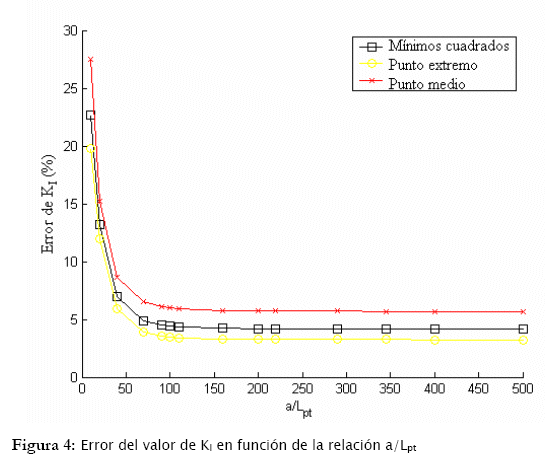
En la Fig. 3 se muestra la influencia del número de elementos de contorno en el error del factor de intensidad de tensiones, L_pt representa la longitud del elemento de contorno de la punta de la fisura, se observa que el número de elementos de contorno usado en la definición del problema analizado prácticamente no tiene influencia en el resultado del cálculo de K_I. También fue estudiada la influencia del tamaño relativo del elemento de contorno de la punta de la fisura con relación a la longitud de la fisura, relación a/L_pt, los resultados para las Ecs. (15) y (16) están mostrados en la Fig. 4.

 

 

3    Factor de intensidad de tensiones para las probetas.

3.1 M(T)

Para la estimación analítica del factor de intensidad de tensiones K_I de configuraciones geométricas comunes como es el caso de las probetas estudiadas en este trabajo se aplica la Ec. (3). En la Fig. 1 se muestran las relaciones geométricas de las probetas investigadas. Tal como se mencionó las funciones F_I pueden ser encontradas en manuales especializados, para probetas tipo M(T), el manual de [6] recomienda:

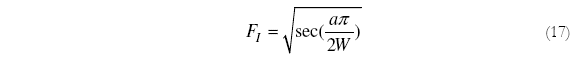
Una de las desventajas de las ecuaciones proporcionadas por el manual Murakami es que estas ecuaciones no llevan en cuenta una longitud finita de las probetas, esto aspecto induce errores mayores en los resultados. Según el manual de [1], para probetas tipo M(T) y 2W = L, la función F_I recomendada es:

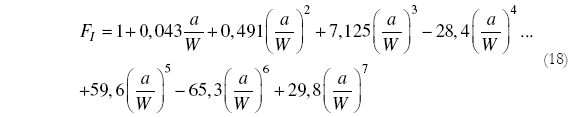
3.2 SE(T)

Según [6], para probetas SE(T) tenemos:

El manual de [1], para probetas SE(T) y 2W = L, recomienda el uso de la misma Ec. (19)

3.3 DE(T)

Para probetas tipo DE(T), [6] propone:

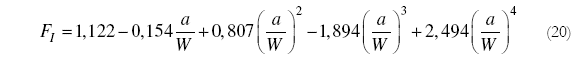
Por otro lado, [1] para probetas DE(T) y 2W= L proponen el uso de la Ec. (21).

 

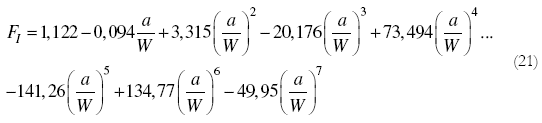
4    Ejemplos numéricos

4.1 M(T)

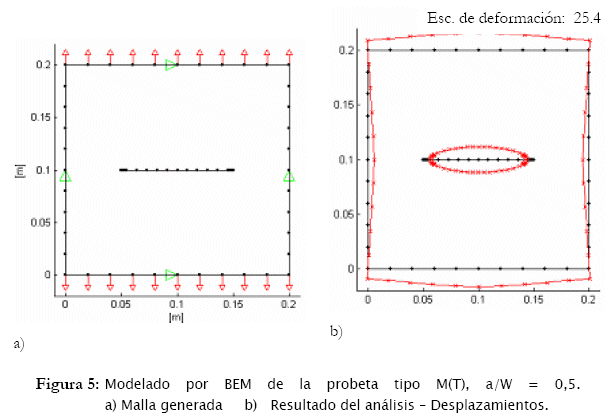
En este ejemplo, la geometría analizada tiene W = 0,1 m, E = 30 GPa, v = 0,3, σ = 100 MPa y la relación de profundidad de la fisura ɑ/W asumió dos valores 0,1 y 0,5. La malla generada para el análisis esta mostrado en la Fig. 5a, en la Fig. 5b se muestra el resultado de los desplazamientos nodales. Los resultados obtenidos de están resumidos en la Tab. 1.

 

4.2 SE(T)

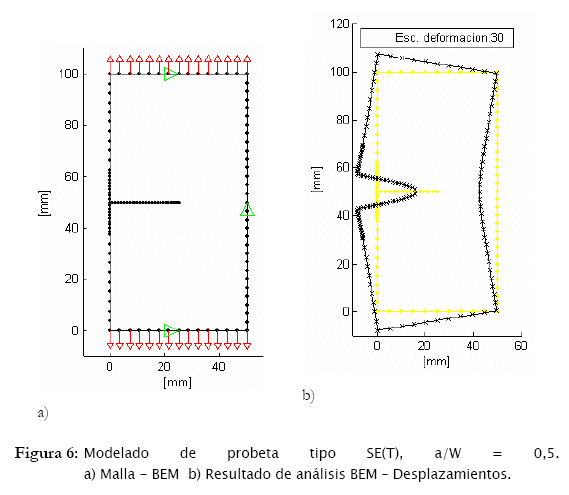
La geometría analizada tiene W = 50 mm, E = 210 GPa, v = 0,3, σ = 200 MPa, L = 100 mm y la relación de profundidad de la fisura ɑ/W= 0,5. Para el modelado por el método BEM, la malla usada y el resultado de los desplazamientos obtenidos se muestran en las Figs. 6a y 6b, la punta de la fisura tiene una relación de ɑ/L_pt = 110.

En la Tab. 2 están resumidos los resultados obtenidos y comparados con los publicados por otros autores.

4.3 DE(T)

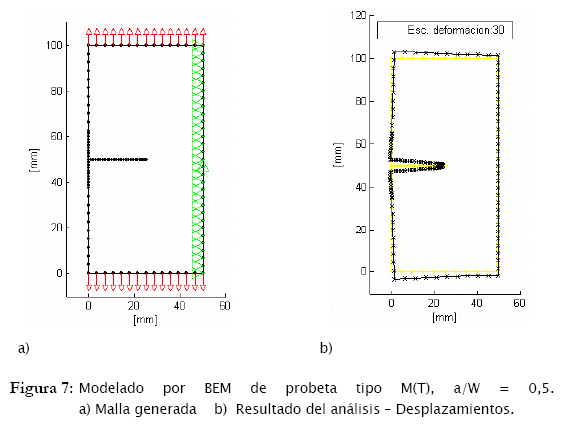
La geometría analizada tiene 2W= 100 mm, E = 210 GPa, v = 0,3, σ = 200 MPa, L = 100 mm y la relación de profundidad de la fisura ɑ/W = 0,5. La probeta tipo DE(T), por la simetría que presenta, puede ser modelada usándose solamente la mitad de la pieza, en este caso el modelo se convierte prácticamente en la misma probeta tipo SE(T) ya analizada en el ejemplo numérico anterior, sin embargo con las condiciones de borde diferentes como es mostrado en la Fig. 7a.

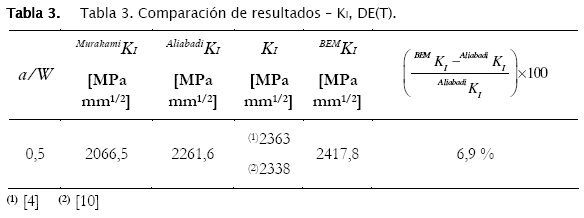
La Fig. 7b muestra el resultado del análisis por Elementos de Contorno, la escala usada para la deformación es la misma que de la Fig. 6b, lo que permite comparar el comportamiento de deformación de ambas probetas. La Tab. 3 muestra los resultados obtenidos de K_I y comparados con los resultados relatados por otros autores.

 

5    Conclusiones

Es posible obtener los factores de intensidad de tensiones usando el método de elementos de contorno "Dual Boundary" con mallas muy simples; sin embargo la implementación numérica del método es bastante compleja. El método de desplazamientos de abertura de la punta de la fisura, usado en este trabajo para la estimación de K_I, es simple en su implementación, pero no permite llegar a valores con errores menores a 3%, no obstante de que se usen mallas muy refinadas. La convergencia numérica del resultado de K_I a partir de relaciones ɑ/L_pt mayores a 100 es muy lenta, por lo que es desaconsejado usar relaciones mayores a esta. Los resultados del valor de K_I obtenidos en este trabajo para las probetas tipo SE (T) y M(T) tienen muy buena correlación con los resultados analíticos y los encontrados por el método de los elementos finitos por otros autores.

 

6    Agradecimientos

Los autores expresan su gratitud a la "Coordenação de Aperfeiçoamento de Pessoal de Nível Superior" (CAPES) por el soporte financiero para la realización de esta investigación.

 

Referencias

[1] Aliabadi, M. H.; Lopez, J. F. L. Database of stress intensity factors. Computational Mechanics Publication, Great Britain, 1996.        [ Links ]

[2] Aliabadi, M. H.; Rooke, D. P. Numerical fracture mechanics. Computational Mechanics Publication, Great Britain, 1991.        [ Links ]

[3] Araujo, T. D.; Birrencourt, T. N.; Roehl, D. & Martha L. F. Numerical estimation of fracture parameters in elastic and elastic-plastic analysis. European congress on computational in applied and engineering - ECCOMAS 2000. Barcelona, Spain, 2000.

[4] Fett, T. Stress intensity factors and weight functions for special crack problems. FZKA 6025, Forschungszentrum Karlsruhe GmbH, Karlsruhe, 1998.        [ Links ]

[5] Hibbitt, Karlsson & Sorensen, Inc. ABAQUS Theory Manual Version 6.3, 2002.        [ Links ]

[6] Murakami, Y. Stress Intensity Factors Handbook. Pergamon Press, Vol. 1, 1987, pp. 3-12.

[7] Salgado, N. K. Boundary Element Methods for damage tolerance design of aircraft structures. Computational Mechanics Publications, Southampton, U. K, 1998.        [ Links ]

[8] Santos, N. C.; Tita, V.; Carvalho, J. Comparison between methods to evaluation J-Integral on 2-D fracture problems. II Congresso Nacional de Engenharia Mecânica. João Pessoa, Brasil, 2002.

[9] Wen, P. H.; Aliabadi, M. H.; Young A. Application of dual reciprocity method to plates and shells, Engineering Analysis with Boundary Elements, 2000, Vol. 24, pp. 583-590.

[10] Zhu, W. X.; Smith, D. J. On the use of displacement extrapolation to obtain crack tip singular stresses and stress intensity factors. Engineering Fracture Mechanics, 1995, Vol. 51, N° 3, pp. 391-400.